Difference between revisions of "Kempf vanishing theorem"
Ulf Rehmann (talk | contribs) m (tex done) |
m (fixing spaces) |
||
| Line 9: | Line 9: | ||
The [[Homogeneous space|homogeneous space]] $ G/B $ | The [[Homogeneous space|homogeneous space]] $ G/B $ | ||
is called the generalized flag variety of $ G $ | is called the generalized flag variety of $ G $ | ||
| − | and it is a projective algebraic variety (cf. also [[Projective algebraic set|Projective algebraic set]]). Let $ \pi : G \rightarrow | + | and it is a projective algebraic variety (cf. also [[Projective algebraic set|Projective algebraic set]]). Let $ \pi : G \rightarrow G/B $ |
be the projection. | be the projection. | ||
For each character $ \chi $ | For each character $ \chi $ | ||
| − | of $ G $( | + | of $ G $ (cf. [[Character of a group|Character of a group]]) one may construct an invertible [[Sheaf|sheaf]] on $ G/B $, |
| − | cf. [[Character of a group|Character of a group]]) one may construct an invertible [[Sheaf|sheaf]] on $ G/B $, | ||
denoted by $ {\mathcal L} _ \chi $. | denoted by $ {\mathcal L} _ \chi $. | ||
Its value on the open subset $ U \subseteq G/B $ | Its value on the open subset $ U \subseteq G/B $ | ||
| Line 25: | Line 24: | ||
$$ | $$ | ||
By the Borel–Weil theorem, its space of global sections is a finite-dimensional representation of $ G $ | By the Borel–Weil theorem, its space of global sections is a finite-dimensional representation of $ G $ | ||
| − | containing a unique irreducible submodule and a unique highest weight vector. The $ B $- | + | containing a unique irreducible submodule and a unique highest weight vector. The $ B $-weight of the highest weight vector is $ - w _{0} ( \chi ) $, |
| − | weight of the highest weight vector is $ - w _{0} ( \chi ) $, | ||
where $ w _{0} $ | where $ w _{0} $ | ||
| − | is the inversion in the [[Weyl group|Weyl group]] of $ G $( | + | is the inversion in the [[Weyl group|Weyl group]] of $ G $ (cf. also [[Weight of a representation of a Lie algebra|Weight of a representation of a Lie algebra]]). This space of global sections is non-zero if and only if $ \chi $ |
| − | cf. also [[Weight of a representation of a Lie algebra|Weight of a representation of a Lie algebra]]). This space of global sections is non-zero if and only if $ \chi $ | ||
is dominant, i.e., if $ \chi $ | is dominant, i.e., if $ \chi $ | ||
is a non-negative integral linear combination of the fundamental dominant weights of $ G $. | is a non-negative integral linear combination of the fundamental dominant weights of $ G $. | ||
| Line 40: | Line 37: | ||
| − | Over fields of characteristic zero, this is a simple consequence of the Bott theorem (see [[#References|[a2]]]), an algebraic proof of which has been given by M. Demazure in 1968 (see [[#References|[a3]]] and [[#References|[a6]]]). An algebraic proof was needed at the time because no proof of the Kodaira vanishing theorem (cf. [[Kodaira theorem|Kodaira theorem]]) over fields of characteristic zero in the algebraic category was then known. (It is known to fail in positive characteristic.) At the time there were two pressing motives for establishing it over fields of positive characteristic. The first was purely rooted in the theory of algebraic groups. Over fields of characteristic zero, algebraic proofs that the character of the $ G $- | + | Over fields of characteristic zero, this is a simple consequence of the Bott theorem (see [[#References|[a2]]]), an algebraic proof of which has been given by M. Demazure in 1968 (see [[#References|[a3]]] and [[#References|[a6]]]). An algebraic proof was needed at the time because no proof of the Kodaira vanishing theorem (cf. [[Kodaira theorem|Kodaira theorem]]) over fields of characteristic zero in the algebraic category was then known. (It is known to fail in positive characteristic.) At the time there were two pressing motives for establishing it over fields of positive characteristic. The first was purely rooted in the theory of algebraic groups. Over fields of characteristic zero, algebraic proofs that the character of the $ G $-module $ H ^{0} ( G/B, {\mathcal L} _ \chi ) $ |
| − | module $ H ^{0} ( G/B, {\mathcal L} _ \chi ) $ | ||
for dominant $ \chi $ | for dominant $ \chi $ | ||
is given by the Weyl character formula had been given by T.A. Springer [[#References|[a17]]] and M. Demazure [[#References|[a4]]]. These proofs imply that the Weyl character gives the [[Euler characteristic|Euler characteristic]] of $ {\mathcal L} _ \chi $ | is given by the Weyl character formula had been given by T.A. Springer [[#References|[a17]]] and M. Demazure [[#References|[a4]]]. These proofs imply that the Weyl character gives the [[Euler characteristic|Euler characteristic]] of $ {\mathcal L} _ \chi $ | ||
Revision as of 08:17, 4 March 2022
Let $ k $
denote an algebraically closed field and let $ G $
be a semi-simple linear algebraic group over $ k $.
Cohomology will always refer to the coherent cohomology on an algebraic variety, that is, Čech cohomology with coefficients in a coherent sheaf of modules. Let $ B $
be a Borel subgroup of $ G $,
i.e., a maximal connected solvable subgroup of $ G $.
The homogeneous space $ G/B $
is called the generalized flag variety of $ G $
and it is a projective algebraic variety (cf. also Projective algebraic set). Let $ \pi : G \rightarrow G/B $
be the projection.
For each character $ \chi $ of $ G $ (cf. Character of a group) one may construct an invertible sheaf on $ G/B $, denoted by $ {\mathcal L} _ \chi $. Its value on the open subset $ U \subseteq G/B $ is $$ {\mathcal L} _ \chi ( U ) = $$ $$ = \left \{ {f : {\pi ^ {- 1} ( U )} \rightarrow k} : {f ( gb ) = f ( g ) \chi ( b ) , g \in G, b \in B} \right \} $$ By the Borel–Weil theorem, its space of global sections is a finite-dimensional representation of $ G $ containing a unique irreducible submodule and a unique highest weight vector. The $ B $-weight of the highest weight vector is $ - w _{0} ( \chi ) $, where $ w _{0} $ is the inversion in the Weyl group of $ G $ (cf. also Weight of a representation of a Lie algebra). This space of global sections is non-zero if and only if $ \chi $ is dominant, i.e., if $ \chi $ is a non-negative integral linear combination of the fundamental dominant weights of $ G $. Then the Kempf vanishing theorem states: Let $ G $ be semi-simple, let $ B $ be a Borel subgroup and let $ \chi $ be a dominant character of $ B $. Then for all $ i > 0 $, $ H ^{i} ( G/B, {\mathcal L} _ \chi ) = ( 0 ) $.
Over fields of characteristic zero, this is a simple consequence of the Bott theorem (see [a2]), an algebraic proof of which has been given by M. Demazure in 1968 (see [a3] and [a6]). An algebraic proof was needed at the time because no proof of the Kodaira vanishing theorem (cf. Kodaira theorem) over fields of characteristic zero in the algebraic category was then known. (It is known to fail in positive characteristic.) At the time there were two pressing motives for establishing it over fields of positive characteristic. The first was purely rooted in the theory of algebraic groups. Over fields of characteristic zero, algebraic proofs that the character of the $ G $-module $ H ^{0} ( G/B, {\mathcal L} _ \chi ) $
for dominant $ \chi $
is given by the Weyl character formula had been given by T.A. Springer [a17] and M. Demazure [a4]. These proofs imply that the Weyl character gives the Euler characteristic of $ {\mathcal L} _ \chi $
even over fields of positive characteristic. Hence Kempf vanishing would have established that $ H ^{0} ( G/B, {\mathcal L} _ \chi ) $
is described by the Weyl character.
For G. Kempf, the result was important to his path-breaking work on the theta-divisors in Jacobians of curves (see [a8]). This work involved computations of Chern classes in which they were represented as pull-backs of Schubert cells. Hence, controlling the cohomological behaviour of line bundles on flag varieties and Schubert cells was critical to his results. Consequently, he established the theorem for special linear groups in [a8]. His methods involved a careful examination of the geometry of Schubert cells and induction on the dimensions of Schubert cells.
Kempf's work inspired the attempt by Lakshmi Bai, C. Musili and C.S. Seshadri in [a12] and subsequent papers to generalize Kempf's methods and to prove vanishing. They failed to obtain vanishing, but that work, along with Demazure's paper [a5] on desingularizing generalized Schubert cells, established the basic geometrical understanding of the geometry of generalized flag varieties which is used by all contemporary researchers in the area.
Kempf continued his work on the problem, [a9], [a10], finally giving the first general proof of vanishing in [a11]. The paper contains a masterful examination of the geometry of the singularities of Schubert cells, the construction of certain special desingularizations and ingenious inductive arguments. It represents the high point of the use of geometrical methods in the area.
The modern approach to the proof of this theorem begins with [a7]. In this paper, W.J. Haboush gave a proof which completely circumvented the geometrical problems and which was based on the observation that the direct image of $ {\mathcal L} _ {( p ^ \nu - 1 ) \rho} $ under the $ \nu $ th Frobenius power is free of rank $ p ^ \nu - 1 $. This same proof was included in H. Andersen's paper [a1], in which the method is also somewhat extended.
The Frobenius methods of [a7] inspired the extremely important series of papers by V.B. Mehta, S. Ramanan and above all A. Ramanathan [a13], [a14], [a15], [a16]. They used the notion of Frobenius splitting to establish the basic geometric vanishing properties of line bundles on generalized flag varieties and generalized Schubert varieties. These have turned out to be the most efficient proofs even of the characteristic zero results, which follows from the results over fields of positive characteristic. In fact, Ramanathan was able to use Frobenius splitting methods in [a16] to repair a serious error in [a5] discovered by V. Kac in the early 1980s.
See also Flag structure; Schubert variety; Representation theory; Character formula.
References
| [a1] | H.H. Andersen, "The Frobenius morphism on the cohomology of homogeneous vector bundles on 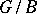 " Ann. of Math. (2) , 112 (1980) pp. 113–121 MR0584076 Zbl 0421.20016 " Ann. of Math. (2) , 112 (1980) pp. 113–121 MR0584076 Zbl 0421.20016 |
| [a2] | R. Bott, "Homogeneous vector bundles" Ann. of Math. (2) , 66 (1957) pp. 203–248 MR0089473 Zbl 0094.35701 |
| [a3] | M. Demazure, "Une démonstration algébrique d'une théorème de Bott" Invent. Math. , 5 (1968) pp. 349–356 |
| [a4] | M. Demazure, "Sur la formule des charactères de H. Weyl" Invent. Math. , 9 (1969) pp. 249–252 |
| [a5] | M. Demazure, "Desingularization des varietés de Schubert généralisées" Ann. Sci. Ecole Norm. Sup. Ser. 4 , 7 (1974) pp. 53–88 |
| [a6] | M. Demazure, "A very simple proof of Bott's theorem" Invent. Math. , 33 (1976) pp. 271–272 MR414569 |
| [a7] | W.J. Haboush, "A short proof of the Kempf vanishing theorem" Invent. Math. , 56 (1980) pp. 109–112 MR0558862 Zbl 0432.14027 |
| [a8] | G. Kempf, "Schubert methods with an application to algebraic curves" , Math. Centre , Amsterdam (1971) (mimeographed notes) Zbl 0223.14018 |
| [a9] | G. Kempf, D. Laksov, "The determinental formula of Schubert calculus" Acta Math. , 132 (1974) pp. 153–162 |
| [a10] | G. Kempf, etAAsal., "Vanishing theorems for flag manifolds" Amer. J. Math. , 98 (1976) pp. 325–331 MR0409493 Zbl 0338.14019 |
| [a11] | G. Kempf, etAAsal., "Linear systems on homogeneous spaces" Ann. of Math. , 103 (1976) pp. 557–591 MR0409474 Zbl 0327.14016 |
| [a12] | Lakshmi Bai, C. Musili, C.S. Seshadri, "Cohomology of line bundles on 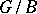 " Ann. Sci. Ecole Norm. Sup. Ser. 4 , 7 (1974) pp. 89–137 MR0354698 Zbl 0338.14017 " Ann. Sci. Ecole Norm. Sup. Ser. 4 , 7 (1974) pp. 89–137 MR0354698 Zbl 0338.14017 |
| [a13] | V.B. Mehta, A. Ramanathan, etAAsal., "Frobenius splitting and cohomology vanishing for Schubert varieties" Ann. of Math. (2) , 122 (1985) pp. 27–40 MR0799251 Zbl 0601.14043 |
| [a14] | V.B. Mehta, A. Ramanathan, etAAsal., "Schubert varieties in 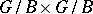 " Compositio Math. , 67 (1988) pp. 355–358 MR0959217 Zbl 0665.14020 " Compositio Math. , 67 (1988) pp. 355–358 MR0959217 Zbl 0665.14020 |
| [a15] | S. Ramanan, A. Ramanathan, "Projective normality of flag varieties and Schubert varieties" Invent. Math. , 79 (1985) pp. 217–114 MR0778124 Zbl 0553.14023 |
| [a16] | A. Ramanathan, "Schubert varieties are arithmetically Cohen–Macaulay" Invent. Math. , 80 (1985) pp. 283–294 MR0788411 Zbl 0541.14039 |
| [a17] | T.A. Springer, "Weyl's character formula for algebraic groups" Invent. Math. , 5 (1968) pp. 85–105 MR227178 |
Kempf vanishing theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kempf_vanishing_theorem&oldid=52175