Difference between revisions of "Symmetric function"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
m (fixing dots) |
||
| Line 12: | Line 12: | ||
A function that does not change under any permutation of its independent variables. The following are examples of symmetric functions: $ x _ {1} + \dots + x _ {n} $, | A function that does not change under any permutation of its independent variables. The following are examples of symmetric functions: $ x _ {1} + \dots + x _ {n} $, | ||
| − | $ x _ {1} \ | + | $ x _ {1} \cdots x _ {n} $, |
$$ | $$ | ||
\sum _ {1 \leq i < j \leq n } | \sum _ {1 \leq i < j \leq n } | ||
x _ {i} x _ {j} ,\ \ | x _ {i} x _ {j} ,\ \ | ||
| − | \max ( x _ {1} \dots x _ {n} ), | + | \max ( x _ {1}, \dots, x _ {n} ), |
$$ | $$ | ||
| Line 26: | Line 26: | ||
the sum in decimal notation of an arbitrary set of one-digit numbers, a "voting function" , which is characterized by its independent variables taking only two values 1 ( "for" ) and 0 ( "against" ), and the function itself is put equal to 1 if more than half of its independent variables are 1 and is put equal to 0 otherwise. Trivial examples of symmetric functions are constant functions and a function of one variable. | the sum in decimal notation of an arbitrary set of one-digit numbers, a "voting function" , which is characterized by its independent variables taking only two values 1 ( "for" ) and 0 ( "against" ), and the function itself is put equal to 1 if more than half of its independent variables are 1 and is put equal to 0 otherwise. Trivial examples of symmetric functions are constant functions and a function of one variable. | ||
| − | Any non-constant symmetric function is essentially dependent on all its variables. Thus, the addition of inessential variables other than constants makes a function non-symmetric, and their removal may make it symmetric. Thus, the concept of a symmetric function relies on an exact indication of all its variables. A simple criterion for the symmetry of a function $ f ( x _ {1} \dots x _ {n} ) $ | + | Any non-constant symmetric function is essentially dependent on all its variables. Thus, the addition of inessential variables other than constants makes a function non-symmetric, and their removal may make it symmetric. Thus, the concept of a symmetric function relies on an exact indication of all its variables. A simple criterion for the symmetry of a function $ f ( x _ {1}, \dots, x _ {n} ) $ |
is that the following two equations hold simultaneously: | is that the following two equations hold simultaneously: | ||
$$ | $$ | ||
| − | f ( x _ {1} , x _ {2} , x _ {3} \dots x _ {n} ) = \ | + | f ( x _ {1} , x _ {2} , x _ {3}, \dots, x _ {n} ) = \ |
| − | f ( x _ {2} , x _ {1} , x _ {3} \dots x _ {n} ), | + | f ( x _ {2} , x _ {1} , x _ {3}, \dots, x _ {n} ), |
$$ | $$ | ||
$$ | $$ | ||
| − | f ( x _ {1} , x _ {2} , x _ {3} \dots x _ {n} ) = f | + | f ( x _ {1} , x _ {2} , x _ {3}, \dots, x _ {n} ) = f |
| − | ( x _ {n} , x _ {1} , x _ {2} \dots x _ {n - 1 } ) | + | ( x _ {n} , x _ {1} , x _ {2}, \dots, x _ {n - 1 } ) |
$$ | $$ | ||
| Line 43: | Line 43: | ||
$$ | $$ | ||
| − | f ( x _ {1} \dots x _ {i} , x _ {i + 1 } \dots x _ {n} ) = \ | + | f ( x _ {1}, \dots, x _ {i} , x _ {i + 1 }, \dots, x _ {n} ) = \ |
| − | f ( x _ {1} \dots x _ {i + 1 } , x _ {i} \dots x _ {n} ), | + | f ( x _ {1}, \dots, x _ {i + 1 } , x _ {i}, \dots, x _ {n} ), |
$$ | $$ | ||
| Line 50: | Line 50: | ||
$$ | $$ | ||
| − | f ( x _ {1} , x _ {2} \dots x _ {n - 1 } , x _ {n} ) = \ | + | f ( x _ {1} , x _ {2}, \dots, x _ {n - 1 } , x _ {n} ) = \ |
| − | f ( x _ {n} , x _ {2} \dots x _ {n - 1 } , x _ {1} ). | + | f ( x _ {n} , x _ {2}, \dots, x _ {n - 1 } , x _ {1} ). |
$$ | $$ | ||
| Line 66: | Line 66: | ||
$$ | $$ | ||
| − | f( x _ {1} \dots x _ {n} ) = g( s _ {1} ( x) \dots s _ {n} ( x)), | + | f( x _ {1}, \dots, x _ {n} ) = g( s _ {1} ( x), \dots, s _ {n} ( x)), |
$$ | $$ | ||
[[#References|[a1]]]. More generally, let $ G $ | [[#References|[a1]]]. More generally, let $ G $ | ||
be a compact group acting linearly on $ \mathbf R ^ {n} $, | be a compact group acting linearly on $ \mathbf R ^ {n} $, | ||
| − | and let $ \rho _ {1} \dots \rho _ {m} $ | + | and let $ \rho _ {1}, \dots, \rho _ {m} $ |
| − | be homogeneous generators of the ring of invariants $ \mathbf R [ x _ {1} \dots x _ {n} ] ^ {G} $. | + | be homogeneous generators of the ring of invariants $ \mathbf R [ x _ {1}, \dots, x _ {n} ] ^ {G} $. |
Let $ \rho : \mathbf R ^ {m} \rightarrow \mathbf R ^ {n} $ | Let $ \rho : \mathbf R ^ {m} \rightarrow \mathbf R ^ {n} $ | ||
| − | be the corresponding mapping, $ x \mapsto ( \rho _ {1} ( x) \dots \rho _ {m} ( x)) $. | + | be the corresponding mapping, $ x \mapsto ( \rho _ {1} ( x), \dots, \rho _ {m} ( x)) $. |
Then | Then | ||
Revision as of 12:31, 28 February 2022
A function that does not change under any permutation of its independent variables. The following are examples of symmetric functions: $ x _ {1} + \dots + x _ {n} $,
$ x _ {1} \cdots x _ {n} $,
$$ \sum _ {1 \leq i < j \leq n } x _ {i} x _ {j} ,\ \ \max ( x _ {1}, \dots, x _ {n} ), $$
$$ x _ {1} + \dots + x _ {n} ( \mathop{\rm mod} m), $$
the sum in decimal notation of an arbitrary set of one-digit numbers, a "voting function" , which is characterized by its independent variables taking only two values 1 ( "for" ) and 0 ( "against" ), and the function itself is put equal to 1 if more than half of its independent variables are 1 and is put equal to 0 otherwise. Trivial examples of symmetric functions are constant functions and a function of one variable.
Any non-constant symmetric function is essentially dependent on all its variables. Thus, the addition of inessential variables other than constants makes a function non-symmetric, and their removal may make it symmetric. Thus, the concept of a symmetric function relies on an exact indication of all its variables. A simple criterion for the symmetry of a function $ f ( x _ {1}, \dots, x _ {n} ) $ is that the following two equations hold simultaneously:
$$ f ( x _ {1} , x _ {2} , x _ {3}, \dots, x _ {n} ) = \ f ( x _ {2} , x _ {1} , x _ {3}, \dots, x _ {n} ), $$
$$ f ( x _ {1} , x _ {2} , x _ {3}, \dots, x _ {n} ) = f ( x _ {n} , x _ {1} , x _ {2}, \dots, x _ {n - 1 } ) $$
or, equivalently, that $ n- 1 $ of the following equations hold:
$$ f ( x _ {1}, \dots, x _ {i} , x _ {i + 1 }, \dots, x _ {n} ) = \ f ( x _ {1}, \dots, x _ {i + 1 } , x _ {i}, \dots, x _ {n} ), $$
together with
$$ f ( x _ {1} , x _ {2}, \dots, x _ {n - 1 } , x _ {n} ) = \ f ( x _ {n} , x _ {2}, \dots, x _ {n - 1 } , x _ {1} ). $$
Symmetric functions are related to symmetric polynomials (cf. Symmetric polynomial). Every rational symmetric function (over a field of characteristic 0) is the quotient of two symmetric polynomials. Any Boolean symmetric function takes equal values on sets of its arguments containing an equal number of identities. These functions play a major role in mathematical cybernetics and its applications and, in particular, they crop up in the schematic realization of arithmetical and other operations.
References
| [1] | B.L. van der Waerden, "Algebra" , 1–2 , Springer (1967–1971) (Translated from German) MR0263582 Zbl 1032.00001 Zbl 1032.00002 |
| [2] | S.V. Yablonskii, "Introduction to discrete mathematics" , Moscow (1979) (In Russian) MR0563327 |
Comments
The theorem that a symmetric polynomial is a polynomial in the elementary symmetric functions is also known as Newton's theorem. Similar statements hold for continuous functions, holomorphic functions and $ C ^ \infty $- functions (smooth functions). E.g., if $ f: \mathbf R ^ {n} \rightarrow \mathbf R $ is a symmetric smooth function, then there is a smooth function $ g: \mathbf R ^ {n} \rightarrow \mathbf R $ such that
$$ f( x _ {1}, \dots, x _ {n} ) = g( s _ {1} ( x), \dots, s _ {n} ( x)), $$
[a1]. More generally, let $ G $ be a compact group acting linearly on $ \mathbf R ^ {n} $, and let $ \rho _ {1}, \dots, \rho _ {m} $ be homogeneous generators of the ring of invariants $ \mathbf R [ x _ {1}, \dots, x _ {n} ] ^ {G} $. Let $ \rho : \mathbf R ^ {m} \rightarrow \mathbf R ^ {n} $ be the corresponding mapping, $ x \mapsto ( \rho _ {1} ( x), \dots, \rho _ {m} ( x)) $. Then
$$ \rho ^ {*} : C ^ \infty ( \mathbf R ^ {m} ) \rightarrow C ^ \infty ( \mathbf R ^ {n} ) ^ {G} $$
is surjective, [a2], the fundamental theorem for smooth invariant functions. This result relies on the Malgrange preparation theorem ( $ C ^ \infty $ preparation theorem, smooth preparation theorem), the $ C ^ \infty $ analogue of the Weierstrass preparation theorem (cf. Weierstrass theorem 4)).
References
| [a1] | G. Glaeser, "Fonctions composées différentiables" Ann. of Math. , 77 (1963) pp. 193–209 MR0188382 MR0143058 Zbl 0202.41503 Zbl 0106.31302 |
| [a2] | G. Schwarz, "Smooth functions invariant under the action of a compact Lie group" Topology , 14 (1975) pp. 63–68 MR0370643 Zbl 0297.57015 |
| [a3] | M. Golubitsky, "Stable mappings and their singularities" , Springer (1973) pp. 108ff MR0341518 Zbl 0294.58004 |
| [a4] | V. Poénaru, "Singularités 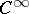 en présence de symmétrie" , Springer (1976) pp. 3–58 en présence de symmétrie" , Springer (1976) pp. 3–58 |
Symmetric function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Symmetric_function&oldid=52132