Difference between revisions of "Spectral geometry of Riemannian submersions"
(Importing text file) |
m (AUTOMATIC EDIT (latexlist): Replaced 24 formulas out of 25 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 25 formulas, 24 were replaced by TEX code.--> | |
| + | |||
| + | {{TEX|semi-auto}}{{TEX|partial}} | ||
| + | Let $\pi : Z \rightarrow Y$ be a Riemannian [[Submersion|submersion]]. Let $D _ { Y }$ and $D _ { Z }$ be operators of Laplace type (cf. also [[Laplace operator|Laplace operator]]) on $Y$ and $Z$ on bundles $V _ { Y }$ and $V _ { Z }$. Let $E ( \lambda , D _ { Y } )$ and $E ( \lambda , D _ { \operatorname {Z} } )$ be the corresponding eigenspaces. Assume given a pull-back <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s120/s120210/s12021010.png"/> from $V _ { Y }$ to $V _ { Z }$. One wants to have examples where there exists | ||
| + | |||
| + | \begin{equation} \tag{a1} 0 \neq \phi \in E ( \lambda , D _ { Y } ) \text { with } \pi ^ { * } \phi \in E ( \mu , D _ { Z } ). \end{equation} | ||
One also wants to know when | One also wants to know when | ||
| − | + | \begin{equation} \tag{a2} \pi ^ { * } E ( \lambda , D _ { Y } ) \subset E ( \mu ( \lambda ) , D _ { Z } ). \end{equation} | |
| − | Let | + | Let $\pi : S ^ { 3 } \rightarrow S ^ { 2 }$ and let $\nu_2$ be the volume element on $S ^ { 2 }$. Let $\Delta ^ { p }$ be the Laplace–Beltrami operator (cf. also [[Laplace–Beltrami equation|Laplace–Beltrami equation]]). Y. Muto [[#References|[a8]]], [[#References|[a7]]] observed that |
| − | + | \begin{equation*} 0 \neq \nu _ { 2 } \in E ( 0 , \Delta _ { S^2 } ^ { 2 } ) \end{equation*} | |
| − | + | \begin{equation*} \pi ^ { * } \nu _ { 2 } \in E ( \mu , \Delta _ { S^3 } ^ { 2 } ) \end{equation*} | |
| − | for | + | for $\mu \neq 0$; he also gave other examples involving principal fibre bundles. |
| − | S.I. Goldberg and T. Ishihara [[#References|[a2]]] and B. Watson [[#References|[a9]]] studied this question and determined some conditions to ensure that (a2) holds with | + | S.I. Goldberg and T. Ishihara [[#References|[a2]]] and B. Watson [[#References|[a9]]] studied this question and determined some conditions to ensure that (a2) holds with $\mu ( \lambda ) = \lambda$ for all $\lambda$; this work was later extended in [[#References|[a5]]] for the real Laplacian and in [[#References|[a3]]] for the complex Laplacian. If (a1) holds for a single eigenvalue, then $\lambda \leq \mu$ (eigenvalues cannot decrease). See also [[#References|[a1]]] for a discussion of the case in which the fibres are totally geodesic. See [[#References|[a6]]] for related results in the spin setting. For a survey of the field, see [[#References|[a4]]]. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> L. Berard Bergery, J.P. Bourguignon, "Laplacians and Riemannian submersions with totally geodesic fibers" ''Illinois J. Math.'' , '''26''' (1982) pp. 181–200</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> S.I. Goldberg, T. Ishihara, "Riemannian submersions commuting with the Laplacian" ''J. Diff. Geom.'' , '''13''' (1978) pp. 139–144</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> P. Gilkey, J. Leahy, J.H. Park, "The eigenforms of the complex Laplacian for a holomorphic Hermitian submersion" ''Nagoya Math. J.'' (to appear)</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> P. Gilkey, J. Leahy, J.H. Park, "Spinors, spectral geometry, and Riemannian submersions" , ''Lecture Notes'' , '''40''' , Research Inst. Math., Global Analysis Research Center, Seoul Nat. Univ. (1998)</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> P. Gilkey, J.H. Park, "Riemannian submersions which preserve the eigenforms of the Laplacian" ''Illinois J. Math.'' , '''40''' (1996) pp. 194–201</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> A. Moroianu, "Opérateur de Dirac et Submersions Riemanniennes" ''Thesis École Polytechn. Palaiseau'' (1996)</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> Y. Muto, "Riemannian submersion and the Laplace–Beltrami operator" ''Kodai Math. J.'' , '''1''' (1978) pp. 329–338</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> Y. Muto, "Some eigenforms of the Laplace–Beltrami operators in a Riemannian submersion" ''J. Korean Math. Soc.'' , '''15''' (1978) pp. 39–57</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> B. Watson, "Manifold maps commuting with the Laplacian" ''J. Diff. Geom.'' , '''8''' (1973) pp. 85–94</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> Y. Muto, "$\delta$ commuting mappings and Betti numbers" ''Tôhoku Math. J.'' , '''27''' (1975) pp. 135–152</td></tr></table> |
Revision as of 17:02, 1 July 2020
Let $\pi : Z \rightarrow Y$ be a Riemannian submersion. Let $D _ { Y }$ and $D _ { Z }$ be operators of Laplace type (cf. also Laplace operator) on $Y$ and $Z$ on bundles $V _ { Y }$ and $V _ { Z }$. Let $E ( \lambda , D _ { Y } )$ and $E ( \lambda , D _ { \operatorname {Z} } )$ be the corresponding eigenspaces. Assume given a pull-back 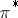 from $V _ { Y }$ to $V _ { Z }$. One wants to have examples where there exists
from $V _ { Y }$ to $V _ { Z }$. One wants to have examples where there exists
\begin{equation} \tag{a1} 0 \neq \phi \in E ( \lambda , D _ { Y } ) \text { with } \pi ^ { * } \phi \in E ( \mu , D _ { Z } ). \end{equation}
One also wants to know when
\begin{equation} \tag{a2} \pi ^ { * } E ( \lambda , D _ { Y } ) \subset E ( \mu ( \lambda ) , D _ { Z } ). \end{equation}
Let $\pi : S ^ { 3 } \rightarrow S ^ { 2 }$ and let $\nu_2$ be the volume element on $S ^ { 2 }$. Let $\Delta ^ { p }$ be the Laplace–Beltrami operator (cf. also Laplace–Beltrami equation). Y. Muto [a8], [a7] observed that
\begin{equation*} 0 \neq \nu _ { 2 } \in E ( 0 , \Delta _ { S^2 } ^ { 2 } ) \end{equation*}
\begin{equation*} \pi ^ { * } \nu _ { 2 } \in E ( \mu , \Delta _ { S^3 } ^ { 2 } ) \end{equation*}
for $\mu \neq 0$; he also gave other examples involving principal fibre bundles.
S.I. Goldberg and T. Ishihara [a2] and B. Watson [a9] studied this question and determined some conditions to ensure that (a2) holds with $\mu ( \lambda ) = \lambda$ for all $\lambda$; this work was later extended in [a5] for the real Laplacian and in [a3] for the complex Laplacian. If (a1) holds for a single eigenvalue, then $\lambda \leq \mu$ (eigenvalues cannot decrease). See also [a1] for a discussion of the case in which the fibres are totally geodesic. See [a6] for related results in the spin setting. For a survey of the field, see [a4].
References
| [a1] | L. Berard Bergery, J.P. Bourguignon, "Laplacians and Riemannian submersions with totally geodesic fibers" Illinois J. Math. , 26 (1982) pp. 181–200 |
| [a2] | S.I. Goldberg, T. Ishihara, "Riemannian submersions commuting with the Laplacian" J. Diff. Geom. , 13 (1978) pp. 139–144 |
| [a3] | P. Gilkey, J. Leahy, J.H. Park, "The eigenforms of the complex Laplacian for a holomorphic Hermitian submersion" Nagoya Math. J. (to appear) |
| [a4] | P. Gilkey, J. Leahy, J.H. Park, "Spinors, spectral geometry, and Riemannian submersions" , Lecture Notes , 40 , Research Inst. Math., Global Analysis Research Center, Seoul Nat. Univ. (1998) |
| [a5] | P. Gilkey, J.H. Park, "Riemannian submersions which preserve the eigenforms of the Laplacian" Illinois J. Math. , 40 (1996) pp. 194–201 |
| [a6] | A. Moroianu, "Opérateur de Dirac et Submersions Riemanniennes" Thesis École Polytechn. Palaiseau (1996) |
| [a7] | Y. Muto, "Riemannian submersion and the Laplace–Beltrami operator" Kodai Math. J. , 1 (1978) pp. 329–338 |
| [a8] | Y. Muto, "Some eigenforms of the Laplace–Beltrami operators in a Riemannian submersion" J. Korean Math. Soc. , 15 (1978) pp. 39–57 |
| [a9] | B. Watson, "Manifold maps commuting with the Laplacian" J. Diff. Geom. , 8 (1973) pp. 85–94 |
| [a10] | Y. Muto, "$\delta$ commuting mappings and Betti numbers" Tôhoku Math. J. , 27 (1975) pp. 135–152 |
Spectral geometry of Riemannian submersions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spectral_geometry_of_Riemannian_submersions&oldid=50441