Difference between revisions of "Schur group"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
m (AUTOMATIC EDIT (latexlist): Replaced 36 formulas out of 37 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 37 formulas, 36 were replaced by TEX code.--> | |
| − | Schur | + | {{TEX|semi-auto}}{{TEX|partial}} |
| + | Let $F$ be a [[Field|field]]. The Schur group $S ( F )$ of $F$ is the subgroup of the [[Brauer group|Brauer group]] $B ( F )$ consisting of those classes of centrally simple $F$-algebras that occur in the [[Group algebra|group algebra]] $F G$ of some [[Finite group|finite group]] $G$. Since the Schur indices for $G$ are trivial in prime characteristic (Wedderburn's theorem; cf. also [[Schur index|Schur index]]), one may assume that $\operatorname { char } ( F ) = 0$. By Brauer's theorem (cf. [[Schur index|Schur index]]), the field $\mathbf{Q} (\operatorname{exp} ( G ) )$ of $\operatorname{exp} ( G )$th roots of unity is a splitting field for $G$. Thus, the study of $S ( F )$ essentially is reduced to the cases where $F$ is an algebraic number field (finite over the rational numbers; cf. also [[Algebraic number|Algebraic number]]; [[Number field|Number field]]) or a completion of such an $F$ with regard to an (infinite or finite) prime. | ||
| − | More detailed investigations of the underlying cyclotomic algebras have been carried out in [[#References|[a1]]]. An alternative approach can be found in [[#References|[a2]]]. Explicit generators for | + | Considering direct products of groups and groups with opposite multiplication shows that $S ( F )$ is indeed a subgroup of $B ( F )$. The celebrated Brauer–Witt theorem implies that the elements of $S ( F )$ are represented by cyclotomic algebras. These are crossed products of fields with Galois groups (cf. also [[Galois group|Galois group]]), in the sense of E. Noether, where the factor sets have finite order. |
| + | |||
| + | Schur indices over the real numbers are computed by means of the Frobenius–Schur count of involutions. Let $L | F$ be a [[Galois extension|Galois extension]] of $p$-adic number fields for some prime number $p$, with group $\Gamma$, and let $e = e ( L | F )$ be the ramification index and let $U _ { L }$ be the group of units in $L$. Then $H ^ { 2 } ( \Gamma , U _ { L } )$ is the (cyclic) subgroup of $B ( F )$ of order $e$. It follows that $S ( F )$ has order dividing $e ( F ( p ) | F )$ when $p$ is odd and dividing $e ( F ( 4 ) | F )$ otherwise. | ||
| + | |||
| + | More detailed investigations of the underlying cyclotomic algebras have been carried out in [[#References|[a1]]]. An alternative approach can be found in [[#References|[a2]]]. Explicit generators for $S ( F )$ in terms of "Schur groups" have been given in [[#References|[a3]]]. | ||
These "Schur groups" occur as terminal reduction steps by repeated application of the Brauer–Witt theorem over local fields. They are the smallest groups admitting characters with non-trivial Schur index, and they appear as sections in any finite group having irreducible characters with non-trivial Schur index. In fact, one has a substitute for the concept of a cyclotomic algebra from the point of view of group representations and characters. There is also a close relationship to [[Clifford theory|Clifford theory]] (of simple modules). | These "Schur groups" occur as terminal reduction steps by repeated application of the Brauer–Witt theorem over local fields. They are the smallest groups admitting characters with non-trivial Schur index, and they appear as sections in any finite group having irreducible characters with non-trivial Schur index. In fact, one has a substitute for the concept of a cyclotomic algebra from the point of view of group representations and characters. There is also a close relationship to [[Clifford theory|Clifford theory]] (of simple modules). | ||
| − | The theory has numerous applications concerning the behaviour of the Schur index | + | The theory has numerous applications concerning the behaviour of the Schur index $m ( \chi )$ of an irreducible character <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130130/s13013035.png"/> of some finite group (over the rational numbers; cf. also [[Character of a group|Character of a group]]). For example, the Benard–Schacher theorem states that $m ( \chi )$ is a divisor of the number of roots of unity in the value field $\mathbf{Q} ( \chi )$. This leads to interesting block-theoretic consequences (the Feit–Solomon theorem), and to a similar result in Clifford theory. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> T. Yamada, "The Schur subgroup of the Brauer group" , ''Lecture Notes in Mathematics'' , '''397''' , Springer (1974) {{MR|0347957}} {{ZBL|0321.20004}} </td></tr><tr><td valign="top">[a2]</td> <td valign="top"> A. Adem, R.J. Milgram, "Cohomology of finite groups" , Springer (1994) {{MR|1317096}} {{ZBL|0828.55008}} {{ZBL|0820.20060}} </td></tr><tr><td valign="top">[a3]</td> <td valign="top"> U. Riese, P. Schmid, "Schur indices and Schur groups, II" ''J. Algebra'' , '''182''' (1996) pp. 183–200 {{MR|1388863}} {{ZBL|0859.20006}} </td></tr></table> |
Revision as of 16:56, 1 July 2020
Let $F$ be a field. The Schur group $S ( F )$ of $F$ is the subgroup of the Brauer group $B ( F )$ consisting of those classes of centrally simple $F$-algebras that occur in the group algebra $F G$ of some finite group $G$. Since the Schur indices for $G$ are trivial in prime characteristic (Wedderburn's theorem; cf. also Schur index), one may assume that $\operatorname { char } ( F ) = 0$. By Brauer's theorem (cf. Schur index), the field $\mathbf{Q} (\operatorname{exp} ( G ) )$ of $\operatorname{exp} ( G )$th roots of unity is a splitting field for $G$. Thus, the study of $S ( F )$ essentially is reduced to the cases where $F$ is an algebraic number field (finite over the rational numbers; cf. also Algebraic number; Number field) or a completion of such an $F$ with regard to an (infinite or finite) prime.
Considering direct products of groups and groups with opposite multiplication shows that $S ( F )$ is indeed a subgroup of $B ( F )$. The celebrated Brauer–Witt theorem implies that the elements of $S ( F )$ are represented by cyclotomic algebras. These are crossed products of fields with Galois groups (cf. also Galois group), in the sense of E. Noether, where the factor sets have finite order.
Schur indices over the real numbers are computed by means of the Frobenius–Schur count of involutions. Let $L | F$ be a Galois extension of $p$-adic number fields for some prime number $p$, with group $\Gamma$, and let $e = e ( L | F )$ be the ramification index and let $U _ { L }$ be the group of units in $L$. Then $H ^ { 2 } ( \Gamma , U _ { L } )$ is the (cyclic) subgroup of $B ( F )$ of order $e$. It follows that $S ( F )$ has order dividing $e ( F ( p ) | F )$ when $p$ is odd and dividing $e ( F ( 4 ) | F )$ otherwise.
More detailed investigations of the underlying cyclotomic algebras have been carried out in [a1]. An alternative approach can be found in [a2]. Explicit generators for $S ( F )$ in terms of "Schur groups" have been given in [a3].
These "Schur groups" occur as terminal reduction steps by repeated application of the Brauer–Witt theorem over local fields. They are the smallest groups admitting characters with non-trivial Schur index, and they appear as sections in any finite group having irreducible characters with non-trivial Schur index. In fact, one has a substitute for the concept of a cyclotomic algebra from the point of view of group representations and characters. There is also a close relationship to Clifford theory (of simple modules).
The theory has numerous applications concerning the behaviour of the Schur index $m ( \chi )$ of an irreducible character 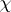 of some finite group (over the rational numbers; cf. also Character of a group). For example, the Benard–Schacher theorem states that $m ( \chi )$ is a divisor of the number of roots of unity in the value field $\mathbf{Q} ( \chi )$. This leads to interesting block-theoretic consequences (the Feit–Solomon theorem), and to a similar result in Clifford theory.
of some finite group (over the rational numbers; cf. also Character of a group). For example, the Benard–Schacher theorem states that $m ( \chi )$ is a divisor of the number of roots of unity in the value field $\mathbf{Q} ( \chi )$. This leads to interesting block-theoretic consequences (the Feit–Solomon theorem), and to a similar result in Clifford theory.
References
| [a1] | T. Yamada, "The Schur subgroup of the Brauer group" , Lecture Notes in Mathematics , 397 , Springer (1974) MR0347957 Zbl 0321.20004 |
| [a2] | A. Adem, R.J. Milgram, "Cohomology of finite groups" , Springer (1994) MR1317096 Zbl 0828.55008 Zbl 0820.20060 |
| [a3] | U. Riese, P. Schmid, "Schur indices and Schur groups, II" J. Algebra , 182 (1996) pp. 183–200 MR1388863 Zbl 0859.20006 |
Schur group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Schur_group&oldid=50160