Difference between revisions of "Bauer-Peschl equation"
m (link) |
m (AUTOMATIC EDIT (latexlist): Replaced 26 formulas out of 27 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 27 formulas, 26 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|partial}} | |
| + | A second-order [[Elliptic partial differential equation|elliptic partial differential equation]] in $\mathbf{R} ^ { 2 }$ (if $\epsilon = 1$) or in the open unit disc $D _ { 1 } \subset \mathbf{R} ^ { 2 }$ (if $\epsilon = - 1$), of the form | ||
| − | + | \begin{equation*} \Delta u + \epsilon \frac { 4 n ( n + 1 ) } { ( 1 + \epsilon ( x ^ { 2 } + y ^ { 2 } ) ) ^ { 2 } } u = 0, \end{equation*} | |
| − | + | \begin{equation*} n \in {\bf N} , \epsilon = \pm 1. \end{equation*} | |
| − | + | By using $z = x + i y$, $\bar{z} = x - i y$, | |
| − | + | \begin{equation*} \frac { \partial } { \partial z } = \frac { 1 } { 2 } \left( \frac { \partial } { \partial x } - i \frac { \partial } { \partial y } \right) , \frac { \partial } { \partial \overline{z} } = \frac { 1 } { 2 } \left( \frac { \partial } { \partial x } + i \frac { \partial } { \partial y } \right), \end{equation*} | |
| − | + | $w ( z ) = u ( x , y )$, one arrives at the standard notation | |
| + | |||
| + | \begin{equation} \tag{a1} \frac { \partial ^ { 2 } w } { \partial z \partial \overline{z}} + \epsilon \frac { n ( n + 1 ) } { ( 1 + \epsilon z \overline{z} ) ^ { 2 } } w = 0, \end{equation} | ||
| + | |||
| + | \begin{equation*} n \in {\bf N} , \epsilon = \pm 1. \end{equation*} | ||
This equation attracted interest from the differential-geometric viewpoint from the times of G. Darboux and H.A. Schwarz. It played an important role in the investigation of differential invariants for certain families of complex functions by E. Peschl ([[#References|[a8]]], [[#References|[a9]]]) and has been treated systematically by a number of authors since then. In particular, the papers of K.W. Bauer [[#References|[a2]]], [[#References|[a1]]] have stimulated further investigations and have been significant. Summaries of the results, including the essential contributions of S. Ruscheweyh, M. Kracht and E. Kreyszig can be found in [[#References|[a3]]] and in [[#References|[a7]]]. | This equation attracted interest from the differential-geometric viewpoint from the times of G. Darboux and H.A. Schwarz. It played an important role in the investigation of differential invariants for certain families of complex functions by E. Peschl ([[#References|[a8]]], [[#References|[a9]]]) and has been treated systematically by a number of authors since then. In particular, the papers of K.W. Bauer [[#References|[a2]]], [[#References|[a1]]] have stimulated further investigations and have been significant. Summaries of the results, including the essential contributions of S. Ruscheweyh, M. Kracht and E. Kreyszig can be found in [[#References|[a3]]] and in [[#References|[a7]]]. | ||
| − | For | + | For $\epsilon = + 1$, equation (a1) transforms by stereographic projection into the equation of [[Spherical harmonics|spherical harmonics]] |
| − | + | \begin{equation*} \frac { 1 } { \operatorname { sin } ^ { 2 } \vartheta } . \frac { \partial ^ { 2 } Y } { \partial \varphi ^ { 2 } } + \frac { 1 } { \operatorname { sin } \vartheta } . \frac { \partial } { \partial \vartheta } \left( \operatorname { sin } \vartheta . \frac { \partial Y } { \partial \vartheta } \right) + \end{equation*} | |
| − | + | \begin{equation*} + n ( n + 1 ) Y = 0. \end{equation*} | |
| − | Separation of variables then readily shows the connection of (a1) with the equations of mathematical physics (cf. also [[Mathematical physics, equations of|Mathematical physics, equations of]]), to wit, the | + | Separation of variables then readily shows the connection of (a1) with the equations of mathematical physics (cf. also [[Mathematical physics, equations of|Mathematical physics, equations of]]), to wit, the $3$-dimensional potential equation |
| − | + | \begin{equation*} \Delta _ { 3 } U = 0 \end{equation*} | |
| − | and the | + | and the $3$-dimensional [[Wave equation|wave equation]] |
| − | + | \begin{equation*} \Delta _ { 3 } U = \frac { \partial ^ { 2 } U } { \partial t ^ { 2 } }. \end{equation*} | |
| − | Analogously, for | + | Analogously, for $\epsilon = - 1$ equation (a1) is connected to the equation of hyperboloid functions and to |
| − | + | \begin{equation*} \Delta_ { 2 } U = \frac { \partial ^ { 2 } U } { \partial t ^ { 2 } }, \end{equation*} | |
| − | the | + | the $2$-dimensional [[Wave equation|wave equation]] (see [[#References|[a2]]], [[#References|[a1]]]). Moreover, (a1) is related to the generalized axially symmetric potential theory, the theory of poly-analytic and poly-harmonic functions, the theory of [[Eisenstein series]], etc. (see [[#References|[a7]]]). |
Motivated by these relations, K.W. Bauer has given detailed representations of the solutions of (a1) by using differential operators: | Motivated by these relations, K.W. Bauer has given detailed representations of the solutions of (a1) by using differential operators: | ||
| − | + | \begin{equation*} w ( z ) = \sum _ { k = 0 } ^ { n } a _ { k } ( z ) . f ^ { ( k ) } ( z ) + \sum _ { k = 0 } ^ { n } b _ { k } ( z ) . \overline { g ^ { ( k ) } ( z ) }, \end{equation*} | |
| − | where | + | where $f$ and $g$ may be arbitrary holomorphic functions (cf. also [[Holomorphic function|Holomorphic function]]). This kind of representation of solutions can be transferred to certain more general equations than (a1), similar to the integral representations of S. Bergman and I.N. Vekua, and facilitates the creation of function theories associated with the classical theory of holomorphic functions (see [[#References|[a2]]], [[#References|[a1]]], [[#References|[a3]]], [[#References|[a4]]], [[#References|[a5]]], [[#References|[a6]]], [[#References|[a7]]]). This allows the treatment of classical problems (e.g. the [[Riemann–Hilbert problem|Riemann–Hilbert problem]], the Cauchy–Kovalevskaya problem, cf. also [[Cauchy–Kovalevskaya theorem|Cauchy–Kovalevskaya theorem]], etc.) for these classes of functions. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> K.W. Bauer, "Über die Lösungen der elliptischen Differentialgleichung $( 1 \pm z \bar{z} ) ^ { 2 } w _ { z \bar{z} } + \lambda w = 0$ I–II" ''J. Reine Angew. Math.'' , '''221''' (1966) pp. 48–84; 176–196</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> K.W. Bauer, "Über eine der Differentialgleichung <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120060/b12006027.png"/> zugeordnete Funktionentheorie" ''Bonner Math. Schriften'' , '''23''' (1965)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> K.W. Bauer, S. Ruscheweyh, "Differential operators for partial differential equations and function theoretic applications" , ''Lecture Notes Math.'' , '''791''' , Springer (1980)</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> P. Berglez, "Darstellung und funktionentheoretische Eigenschaften von Lösungen partieller Differentialgleichungen" ''Habilitationsschrift Techn. Univ. Graz'' (1988)</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> R. Heersink, "Über Lösungsdarstellungen und funktionentheoretische Methoden bei elliptischen Differentialgleichungen" ''Ber. Math. Statist. Sektion Forschungszentrum Graz'' , '''67''' (1976)</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> R. Heersink, "Zur Charakterisierung spezieller Lösungsdarstellungen für elliptische Gleichungen" ''Österr. Akad. d. Wiss., Abt.II'' , '''192''' : 4–7 (1983) pp. 267–293</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> M. Kracht, E. Kreyszig, "Methods of complex analysis in partial differential equations with applications" , Wiley (1988)</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> E. Peschl, "Les invariants differentiels non holomorphes et leur role dans la theorie de fonctions" ''Rend. Sem. Mat. Messina'' , '''1''' (1955) pp. 100–108</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> E. Peschl, "Über die Verwendung von Differentialinvarianten bei gewissen Funktionenfamilien und die Übertragung einer darauf gegründeten Methode auf partielle Differentialgleichungen vom elliptischen Typus" ''Ann. Acad. Sci. Fenn., Ser. A I Math.'' , '''336''' : 6 (1963)</td></tr></table> |
Revision as of 16:45, 1 July 2020
A second-order elliptic partial differential equation in $\mathbf{R} ^ { 2 }$ (if $\epsilon = 1$) or in the open unit disc $D _ { 1 } \subset \mathbf{R} ^ { 2 }$ (if $\epsilon = - 1$), of the form
\begin{equation*} \Delta u + \epsilon \frac { 4 n ( n + 1 ) } { ( 1 + \epsilon ( x ^ { 2 } + y ^ { 2 } ) ) ^ { 2 } } u = 0, \end{equation*}
\begin{equation*} n \in {\bf N} , \epsilon = \pm 1. \end{equation*}
By using $z = x + i y$, $\bar{z} = x - i y$,
\begin{equation*} \frac { \partial } { \partial z } = \frac { 1 } { 2 } \left( \frac { \partial } { \partial x } - i \frac { \partial } { \partial y } \right) , \frac { \partial } { \partial \overline{z} } = \frac { 1 } { 2 } \left( \frac { \partial } { \partial x } + i \frac { \partial } { \partial y } \right), \end{equation*}
$w ( z ) = u ( x , y )$, one arrives at the standard notation
\begin{equation} \tag{a1} \frac { \partial ^ { 2 } w } { \partial z \partial \overline{z}} + \epsilon \frac { n ( n + 1 ) } { ( 1 + \epsilon z \overline{z} ) ^ { 2 } } w = 0, \end{equation}
\begin{equation*} n \in {\bf N} , \epsilon = \pm 1. \end{equation*}
This equation attracted interest from the differential-geometric viewpoint from the times of G. Darboux and H.A. Schwarz. It played an important role in the investigation of differential invariants for certain families of complex functions by E. Peschl ([a8], [a9]) and has been treated systematically by a number of authors since then. In particular, the papers of K.W. Bauer [a2], [a1] have stimulated further investigations and have been significant. Summaries of the results, including the essential contributions of S. Ruscheweyh, M. Kracht and E. Kreyszig can be found in [a3] and in [a7].
For $\epsilon = + 1$, equation (a1) transforms by stereographic projection into the equation of spherical harmonics
\begin{equation*} \frac { 1 } { \operatorname { sin } ^ { 2 } \vartheta } . \frac { \partial ^ { 2 } Y } { \partial \varphi ^ { 2 } } + \frac { 1 } { \operatorname { sin } \vartheta } . \frac { \partial } { \partial \vartheta } \left( \operatorname { sin } \vartheta . \frac { \partial Y } { \partial \vartheta } \right) + \end{equation*}
\begin{equation*} + n ( n + 1 ) Y = 0. \end{equation*}
Separation of variables then readily shows the connection of (a1) with the equations of mathematical physics (cf. also Mathematical physics, equations of), to wit, the $3$-dimensional potential equation
\begin{equation*} \Delta _ { 3 } U = 0 \end{equation*}
and the $3$-dimensional wave equation
\begin{equation*} \Delta _ { 3 } U = \frac { \partial ^ { 2 } U } { \partial t ^ { 2 } }. \end{equation*}
Analogously, for $\epsilon = - 1$ equation (a1) is connected to the equation of hyperboloid functions and to
\begin{equation*} \Delta_ { 2 } U = \frac { \partial ^ { 2 } U } { \partial t ^ { 2 } }, \end{equation*}
the $2$-dimensional wave equation (see [a2], [a1]). Moreover, (a1) is related to the generalized axially symmetric potential theory, the theory of poly-analytic and poly-harmonic functions, the theory of Eisenstein series, etc. (see [a7]).
Motivated by these relations, K.W. Bauer has given detailed representations of the solutions of (a1) by using differential operators:
\begin{equation*} w ( z ) = \sum _ { k = 0 } ^ { n } a _ { k } ( z ) . f ^ { ( k ) } ( z ) + \sum _ { k = 0 } ^ { n } b _ { k } ( z ) . \overline { g ^ { ( k ) } ( z ) }, \end{equation*}
where $f$ and $g$ may be arbitrary holomorphic functions (cf. also Holomorphic function). This kind of representation of solutions can be transferred to certain more general equations than (a1), similar to the integral representations of S. Bergman and I.N. Vekua, and facilitates the creation of function theories associated with the classical theory of holomorphic functions (see [a2], [a1], [a3], [a4], [a5], [a6], [a7]). This allows the treatment of classical problems (e.g. the Riemann–Hilbert problem, the Cauchy–Kovalevskaya problem, cf. also Cauchy–Kovalevskaya theorem, etc.) for these classes of functions.
References
| [a1] | K.W. Bauer, "Über die Lösungen der elliptischen Differentialgleichung $( 1 \pm z \bar{z} ) ^ { 2 } w _ { z \bar{z} } + \lambda w = 0$ I–II" J. Reine Angew. Math. , 221 (1966) pp. 48–84; 176–196 |
| [a2] | K.W. Bauer, "Über eine der Differentialgleichung 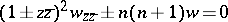 zugeordnete Funktionentheorie" Bonner Math. Schriften , 23 (1965) zugeordnete Funktionentheorie" Bonner Math. Schriften , 23 (1965) |
| [a3] | K.W. Bauer, S. Ruscheweyh, "Differential operators for partial differential equations and function theoretic applications" , Lecture Notes Math. , 791 , Springer (1980) |
| [a4] | P. Berglez, "Darstellung und funktionentheoretische Eigenschaften von Lösungen partieller Differentialgleichungen" Habilitationsschrift Techn. Univ. Graz (1988) |
| [a5] | R. Heersink, "Über Lösungsdarstellungen und funktionentheoretische Methoden bei elliptischen Differentialgleichungen" Ber. Math. Statist. Sektion Forschungszentrum Graz , 67 (1976) |
| [a6] | R. Heersink, "Zur Charakterisierung spezieller Lösungsdarstellungen für elliptische Gleichungen" Österr. Akad. d. Wiss., Abt.II , 192 : 4–7 (1983) pp. 267–293 |
| [a7] | M. Kracht, E. Kreyszig, "Methods of complex analysis in partial differential equations with applications" , Wiley (1988) |
| [a8] | E. Peschl, "Les invariants differentiels non holomorphes et leur role dans la theorie de fonctions" Rend. Sem. Mat. Messina , 1 (1955) pp. 100–108 |
| [a9] | E. Peschl, "Über die Verwendung von Differentialinvarianten bei gewissen Funktionenfamilien und die Übertragung einer darauf gegründeten Methode auf partielle Differentialgleichungen vom elliptischen Typus" Ann. Acad. Sci. Fenn., Ser. A I Math. , 336 : 6 (1963) |
Bauer-Peschl equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bauer-Peschl_equation&oldid=49959