Difference between revisions of "Transfinite diameter"
Ulf Rehmann (talk | contribs) m (Undo revision 49009 by Ulf Rehmann (talk)) Tag: Undo |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | t0936701.png | ||
| + | $#A+1 = 155 n = 1 | ||
| + | $#C+1 = 155 : ~/encyclopedia/old_files/data/T093/T.0903670 Transfinite diameter | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''of a compact set'' | ''of a compact set'' | ||
| − | A characteristic | + | A characteristic $ d = d ( E) $ |
| + | of a compact set $ E $ | ||
| + | in the complex plane serving as a geometric interpretation of the [[Capacity|capacity]] of this set. Let $ E $ | ||
| + | be a compact infinite set in the $ z $- | ||
| + | plane. Then the quantity | ||
| + | |||
| + | $$ \tag{1 } | ||
| + | d _ {n} ( E) = \ | ||
| + | \left \{ | ||
| + | \max _ {z _ {k} , z _ {l} \in E } \ | ||
| + | \prod _ {1 \leq k < l \leq n } | ||
| + | [ z _ {k} , z _ {l} ] | ||
| + | \right \} ^ {2/[ n ( n - 1)] } , | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | n = 2, 3 \dots | ||
| + | $$ | ||
| + | |||
| + | where $ [ a, b] = | a - b | $ | ||
| + | is the Euclidean distance between $ a $ | ||
| + | and $ b $, | ||
| + | is called the $ n $- | ||
| + | th diameter of $ E $. | ||
| + | In particular, $ d _ {2} ( E) $ | ||
| + | is the Euclidean diameter of $ E $. | ||
| + | The points $ z _ {n,1} \dots z _ {n,n} $ | ||
| + | of $ E $ | ||
| + | for which the maximum on the right-hand side of (1) is realized are called the Fekete points (or Vandermonde nodes) for $ E $. | ||
| + | The sequence of quantities $ d _ {n} ( E) $ | ||
| + | is non-increasing: $ d _ {n + 1 } ( E) \leq d _ {n} ( E) $, | ||
| + | $ n = 2, 3 \dots $ | ||
| + | so that the following limit exists: | ||
| + | |||
| + | $$ | ||
| + | \lim\limits _ {n \rightarrow \infty } d _ {n} ( E) = d ( E). | ||
| + | $$ | ||
| − | + | The quantity $ d ( E) $ | |
| + | is also called the transfinite diameter of $ E $. | ||
| + | If $ E $ | ||
| + | is a finite set, then one has $ d ( E) = 0 $. | ||
| + | The transfinite diameter $ d ( E) $, | ||
| + | the [[Chebyshev constant|Chebyshev constant]] $ \tau ( E) $ | ||
| + | and the capacity $ C ( E) $ | ||
| + | are equal: | ||
| − | + | $$ | |
| + | d ( E) = \tau ( E) = C ( E). | ||
| + | $$ | ||
| − | + | The transfinite diameter of a set $ E $ | |
| + | has the following properties: 1) if $ E _ {1} \subset E $, | ||
| + | then $ d ( E _ {1} ) \leq d ( E) $; | ||
| + | 2) if $ a $ | ||
| + | is a fixed complex number and $ E _ {1} = \{ {w } : {w = az, z \in E } \} $, | ||
| + | then $ d ( E _ {1} ) = | a | d ( E) $; | ||
| + | 3) if $ E _ \epsilon $ | ||
| + | is the set of points at a distance at most $ \epsilon $ | ||
| + | from $ E $, | ||
| + | then $ \lim\limits _ {\epsilon \rightarrow 0 } d ( E _ \epsilon ) = d ( E) $; | ||
| + | 4) if $ E ^ {*} $ | ||
| + | is the set of roots of the equation | ||
| − | + | $$ | |
| + | Q ( z) = z ^ {k} + a _ {1} z ^ {k - 1 } + \dots + a _ {k} = w, | ||
| + | $$ | ||
| − | + | where $ Q ( z) $ | |
| + | is a given polynomial and $ w $ | ||
| + | runs through $ E $, | ||
| + | then $ d ( E ^ {*} ) = \{ d ( E) \} ^ {1/k} $. | ||
| + | The transfinite diameter of a circle is equal to its radius; the transfinite diameter of a line segment is equal to a quarter of its length. | ||
| − | + | Let $ E $ | |
| + | be a bounded continuum and let $ D $ | ||
| + | be the component of the complement of $ E $ | ||
| + | with respect to the extended plane that contains the point $ \infty $. | ||
| + | Then the transfinite diameter of $ E $ | ||
| + | is equal to the conformal radius of $ D $( | ||
| + | with respect to $ \infty $; | ||
| + | cf. [[Conformal radius of a domain|Conformal radius of a domain]]). | ||
| − | The | + | The corresponding notions for sets in the hyperbolic and elliptic planes are defined as follows. Consider as a model of the hyperbolic plane the disc $ | z | < 1 $ |
| + | with metric defined by the line element $ ds _ {h} = | dz |/( 1 - | z | ^ {2} ) $ | ||
| + | and suppose that $ E $ | ||
| + | is a closed infinite set in $ | z | < 1 $. | ||
| + | Then the $ n $- | ||
| + | th hyperbolic diameter $ d _ {n,h} ( E) $ | ||
| + | of $ E $ | ||
| + | is defined by (1) in which | ||
| − | + | $$ \tag{2 } | |
| + | [ a, b] = \ | ||
| + | \left | | ||
| − | + | \frac{a - b }{1 - \overline{a}\; b } | |
| + | \ | ||
| + | \right | | ||
| + | $$ | ||
| − | + | is the hyperbolic pseudo-distance between $ a $ | |
| + | and $ b $, | ||
| + | that is, $ [ a, b] = \mathop{\rm tanh} \rho _ {h} ( a, b) $, | ||
| + | where $ \rho _ {h} ( a, b) $ | ||
| + | is the hyperbolic distance between $ a $ | ||
| + | and $ b $ | ||
| + | in $ | z | < 1 $( | ||
| + | see [[Hyperbolic metric|Hyperbolic metric]]). As in the Euclidean case, the sequence $ d _ {n,h} ( E) $ | ||
| + | is non-increasing and the following limit exists: | ||
| − | + | $$ | |
| + | \lim\limits _ {n \rightarrow \infty } d _ {n,h} ( E) = d _ {h} ( E). | ||
| + | $$ | ||
| − | + | It is called the hyperbolic transfinite diameter of $ E $. | |
| + | Define the hyperbolic Chebyshev constant $ \tau _ {h} ( E) $ | ||
| + | and the hyperbolic capacity $ C _ {h} ( E) $ | ||
| + | of $ E $ | ||
| + | via the hyperbolic pseudo-distance (2) between the points of $ | z | < 1 $ | ||
| + | by analogy with the Chebyshev constant $ \tau ( E) $ | ||
| + | and capacity $ C ( E) $ | ||
| + | defined via the Euclidean distance between points of the $ z $- | ||
| + | plane. Then one obtains | ||
| − | + | $$ | |
| + | d _ {h} ( E) = \tau _ {h} ( E) = C _ {h} ( E). | ||
| + | $$ | ||
| − | < | + | The hyperbolic transfinite diameter is invariant under the full group of hyperbolic isometries. If $ E $ |
| + | is a continuum, then there is a simple relationship between the hyperbolic transfinite diameter $ d _ {n} ( E) $ | ||
| + | and conformal mapping. Namely, let $ E $ | ||
| + | be a continuum in the disc $ | z | < 1 $ | ||
| + | such that the complement of $ E $ | ||
| + | with respect to this disc is conformally equivalent to the annulus $ r < | w | < 1 $, | ||
| + | $ 0 < r < 1 $. | ||
| + | Then $ r = d _ {n} ( E) $. | ||
| − | + | Consider as a model of the elliptic plane the extended complex $ z $- | |
| + | plane with the metric of its Riemann sphere $ K $ | ||
| + | of diameter 1, tangent to the $ z $- | ||
| + | plane at the point $ z = 0 $, | ||
| + | that is, the metric defined by the line element | ||
| − | + | $$ | |
| + | ds _ {e} = \ | ||
| − | + | \frac{| dz | }{1 + | z | ^ {2} } | |
| + | ; | ||
| + | $$ | ||
| − | + | furthermore, let the points $ z $ | |
| + | and $ z ^ {*} = - 1/z $ | ||
| + | be identified; these correspond to diametrically-opposite points of $ K $ | ||
| + | under stereographic projection of the extended $ z $- | ||
| + | plane onto $ K $. | ||
| + | Let $ E $ | ||
| + | be a closed infinite set in the extended $ z $- | ||
| + | plane, $ E \cap E ^ {*} = \emptyset $, | ||
| + | where $ E ^ {*} = \{ {- 1/z } : {z \in E } \} $. | ||
| + | Then the $ n $- | ||
| + | th elliptic diameter $ d _ {n,e} ( E) $ | ||
| + | of $ E $ | ||
| + | is defined by (1), in which | ||
| − | + | $$ \tag{3 } | |
| + | [ a, b] = \ | ||
| + | \left | | ||
| − | + | \frac{a - b }{1 + \overline{a}\; b } | |
| + | \ | ||
| + | \right | | ||
| + | $$ | ||
| − | + | is the elliptic pseudo-distance between points $ a $ | |
| + | and $ b $ | ||
| + | of $ E $, | ||
| + | that is, $ [ a, b] = \mathop{\rm tan} \rho _ {e} ( a, b) $, | ||
| + | where $ \rho _ {e} ( a, b) $( | ||
| + | $ < \pi /2 $) | ||
| + | is the elliptic distance between $ a $ | ||
| + | and $ b $. | ||
| + | As in the previous cases, the sequence $ d _ {n,e} ( E) $ | ||
| + | is non-increasing and the following limit, called the elliptic transfinite diameter of $ E $, | ||
| + | exists: | ||
| − | + | $$ | |
| + | \lim\limits _ {n \rightarrow \infty } d _ {n,e} ( E) = d _ {e} ( E). | ||
| + | $$ | ||
| − | + | Define the elliptic Chebyshev constant $ \tau _ {e} ( E) $ | |
| + | and the elliptic capacity $ C _ {e} ( E) $ | ||
| + | of $ E $ | ||
| + | via the elliptic pseudo-distance (3). Then one obtains: | ||
| − | + | $$ | |
| + | d _ {e} ( E) = \tau _ {e} ( E) = C _ {e} ( E). | ||
| + | $$ | ||
| − | + | The elliptic transfinite diameter $ d _ {e} ( E) $ | |
| + | is invariant under the group of fractional-linear transformations | ||
| − | + | $$ | |
| + | z \rightarrow \ | ||
| − | + | \frac{pz + q }{- \overline{q}\; z + p } | |
| + | ,\ \ | ||
| + | | p | ^ {2} + | q | ^ {2} = 1, | ||
| + | $$ | ||
| − | of the extended | + | of the extended $ z $- |
| + | plane onto itself, supplemented by the group of reflections in the elliptic lines. The first of these groups is isomorphic to the group of reflections of $ K $ | ||
| + | about planes passing through its centre. With this definition the elliptic transfinite diameter of $ E $ | ||
| + | is related to conformal mapping in the following way. If $ E $ | ||
| + | is a continuum in the extended $ z $- | ||
| + | plane, $ E \cap E ^ {*} = \emptyset $, | ||
| + | and the complement of $ E \cup E ^ {*} $ | ||
| + | with respect to the extended plane is conformally equivalent to the annulus $ r < | w | < 1/r $, | ||
| + | $ 0 < r < 1 $, | ||
| + | then $ r = d _ {e} ( E) $. | ||
| − | The notion of the transfinite diameter can be generalized to compacta | + | The notion of the transfinite diameter can be generalized to compacta $ E $ |
| + | in a multi-dimensional Euclidean space $ \mathbf R ^ {m} $, | ||
| + | $ m \geq 2 $, | ||
| + | and is connected with [[Potential theory|potential theory]]. Let, for points $ x \in \mathbf R ^ {m} $, | ||
| − | + | $$ | |
| + | H (| x |) = \ | ||
| + | \left \{ | ||
| − | + | \begin{array}{ll} | |
| + | \mathop{\rm ln} { | ||
| + | \frac{1}{| x | } | ||
| + | } & \textrm{ for } m = 2, \\ | ||
| + | { | ||
| + | \frac{1}{| x | ^ {m - 2 } } | ||
| + | } & \textrm{ for } m \geq 3, \\ | ||
| + | \end{array} | ||
| − | + | \right .$$ | |
| − | + | be a fundamental solution of the [[Laplace equation|Laplace equation]], and for the set of points $ ( x _ {j} ) _ {j = 1 } ^ {n} \subset E $, | |
| + | let | ||
| − | + | $$ | |
| + | \chi _ {n} ( E) = \ | ||
| + | \inf | ||
| + | \left \{ { { | ||
| + | \frac{2}{n ( n - 1) } | ||
| + | } | ||
| + | \sum _ {\begin{array}{c} | ||
| + | j, k = 1 \\ | ||
| + | j < k | ||
| + | \end{array} | ||
| + | } ^ { n } | ||
| + | H (| x _ {j} - x _ {k} |) } : { | ||
| + | ( x _ {j} ) _ {j = 1 } ^ {n} \subset E | ||
| + | } \right \} | ||
| + | . | ||
| + | $$ | ||
| − | + | Then for $ m = 2 $ | |
| + | one has | ||
| − | + | $$ | |
| + | d ( E) = C ( E) = \ | ||
| + | \mathop{\rm exp} \left ( - \lim\limits _ {n \rightarrow \infty } \chi _ {n} ( E) \right ) ; | ||
| + | $$ | ||
| + | |||
| + | while for $ m \geq 3 $ | ||
| + | it is expedient (see [[#References|[4]]]) to take | ||
| + | |||
| + | $$ | ||
| + | d ( E) = C ( E) = \ | ||
| + | { | ||
| + | \frac{1}{\lim\limits _ {n \rightarrow \infty } \chi _ {n} ( E) } | ||
| + | } . | ||
| + | $$ | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> M. Fekete, "Ueber die Verteilung der Wurzeln bei gewissen algebraischen Gleichungen mit ganzzahligen Koeffizienten" ''Math. Z.'' , '''17''' (1923) pp. 228–249</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> G. Pólya, G. Szegö, "Ueber den transfiniten Durchmesser (Kapazitätskonstante) von ebenen und räumlichen Punktmengen" ''J. Reine Angew. Math.'' , '''165''' (1931) pp. 4–49</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> G.M. Goluzin, "Geometric theory of functions of a complex variable" , ''Transl. Math. Monogr.'' , '''26''' , Amer. Math. Soc. (1969) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> L. Carleson, "Selected problems on exceptional sets" , v. Nostrand (1967)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> V.I. Smirnov, A.N. Lebedev, "Functions of a complex variable" , M.I.T. (1968) (Translated from Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> M. Tsuji, "Potential theory in modern function theory" , Chelsea, reprint (1959)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> R. Kühnau, "Geometrie der konformen Abbildung auf der hyperbolischen und der elliptischen Ebene" , Deutsch. Verlag Wissenschaft. (1974)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> M. Fekete, "Ueber die Verteilung der Wurzeln bei gewissen algebraischen Gleichungen mit ganzzahligen Koeffizienten" ''Math. Z.'' , '''17''' (1923) pp. 228–249</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> G. Pólya, G. Szegö, "Ueber den transfiniten Durchmesser (Kapazitätskonstante) von ebenen und räumlichen Punktmengen" ''J. Reine Angew. Math.'' , '''165''' (1931) pp. 4–49</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> G.M. Goluzin, "Geometric theory of functions of a complex variable" , ''Transl. Math. Monogr.'' , '''26''' , Amer. Math. Soc. (1969) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> L. Carleson, "Selected problems on exceptional sets" , v. Nostrand (1967)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> V.I. Smirnov, A.N. Lebedev, "Functions of a complex variable" , M.I.T. (1968) (Translated from Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> M. Tsuji, "Potential theory in modern function theory" , Chelsea, reprint (1959)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> R. Kühnau, "Geometrie der konformen Abbildung auf der hyperbolischen und der elliptischen Ebene" , Deutsch. Verlag Wissenschaft. (1974)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | Outer radius is another term for transfinite diameter. See [[#References|[a1]]] for a survey on connections between transfinite diameter, [[Robin constant|Robin constant]] and [[Capacity|capacity]] in | + | Outer radius is another term for transfinite diameter. See [[#References|[a1]]] for a survey on connections between transfinite diameter, [[Robin constant|Robin constant]] and [[Capacity|capacity]] in $ \mathbf R ^ {2} $ |
| + | or $ \mathbf R ^ {n} $. | ||
| − | The notion of transfinite diameter also makes good sense in several complex variables, if interpreted in the correct way: (1) with | + | The notion of transfinite diameter also makes good sense in several complex variables, if interpreted in the correct way: (1) with $ [ a, b] = | a- b | $ |
| + | is a root of a Vandermondian determinant: | ||
| − | + | $$ | |
| + | d _ {n} ( E) = ( \max _ {x ^ {( n ) } | ||
| + | \in E ^ {n} } | V ( x ^ {(} n) ) | ) ^ {2/n( n- 1) } , | ||
| + | $$ | ||
where | where | ||
| − | + | $$ | |
| + | V( x ^ {(} n) ) = \mathop{\rm det} | ||
| + | [ x _ {i} ^ {j} ] _ {\begin{array} {c} | ||
| + | i = 1 \dots n \\ | ||
| + | j= 0 \dots n- 1 | ||
| + | \end{array} | ||
| + | } . | ||
| + | $$ | ||
| − | In | + | In $ \mathbf C ^ {n} $, |
| + | let $ e _ {1} \dots e _ {m _ {n} } $ | ||
| + | be an ordered system of monomials of degree $ \leq n $ | ||
| + | and let $ x ^ {(} n) $ | ||
| + | be a point in $ E ^ {m _ {n} } \subset \mathbf C ^ {m _ {n} } $. | ||
| + | Then $ V ( x ^ {(} n) ) $ | ||
| + | is defined as $ \mathop{\rm det} [ e _ {i} ( x _ {j} )] $, | ||
| + | $ x ^ {n} = ( x _ {1} \dots x _ {m _ {n} } ) $, | ||
| + | and $ d _ {n} ( E) = ( \max _ {x ^ {(} n) \in E ^ {m _ {n} } } V( x ^ {(} n) ) ) ^ {1/ \mathop{\rm deg} V( x ^ {n} ) } $. | ||
| + | The related capacity is the one associated to the complex Monge–Ampère operator. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R.E. Kleinman, "On a unified characterization of capacity" J. Král (ed.) J. Lukeš (ed.) J. Veselý (ed.) , ''Potential theory. Survey and problems (Prague, 1987)'' , ''Lect. notes in math.'' , '''1344''' , Plenum (1988) pp. 103–120</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Klimek, "Pluripotential theory" , Cambridge Univ. Press (1991)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J. Siciak, "Extremal plurisubharmonic functions and capacities in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670159.png" />" , ''Sophia Kokyuroku in Math.'' , '''14''' , Dept. Math. Sophia Univ. Tokyo (1982)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R.E. Kleinman, "On a unified characterization of capacity" J. Král (ed.) J. Lukeš (ed.) J. Veselý (ed.) , ''Potential theory. Survey and problems (Prague, 1987)'' , ''Lect. notes in math.'' , '''1344''' , Plenum (1988) pp. 103–120</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Klimek, "Pluripotential theory" , Cambridge Univ. Press (1991)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J. Siciak, "Extremal plurisubharmonic functions and capacities in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093670/t093670159.png" />" , ''Sophia Kokyuroku in Math.'' , '''14''' , Dept. Math. Sophia Univ. Tokyo (1982)</TD></TR></table> | ||
Revision as of 14:56, 7 June 2020
of a compact set
A characteristic $ d = d ( E) $ of a compact set $ E $ in the complex plane serving as a geometric interpretation of the capacity of this set. Let $ E $ be a compact infinite set in the $ z $- plane. Then the quantity
$$ \tag{1 } d _ {n} ( E) = \ \left \{ \max _ {z _ {k} , z _ {l} \in E } \ \prod _ {1 \leq k < l \leq n } [ z _ {k} , z _ {l} ] \right \} ^ {2/[ n ( n - 1)] } , $$
$$ n = 2, 3 \dots $$
where $ [ a, b] = | a - b | $ is the Euclidean distance between $ a $ and $ b $, is called the $ n $- th diameter of $ E $. In particular, $ d _ {2} ( E) $ is the Euclidean diameter of $ E $. The points $ z _ {n,1} \dots z _ {n,n} $ of $ E $ for which the maximum on the right-hand side of (1) is realized are called the Fekete points (or Vandermonde nodes) for $ E $. The sequence of quantities $ d _ {n} ( E) $ is non-increasing: $ d _ {n + 1 } ( E) \leq d _ {n} ( E) $, $ n = 2, 3 \dots $ so that the following limit exists:
$$ \lim\limits _ {n \rightarrow \infty } d _ {n} ( E) = d ( E). $$
The quantity $ d ( E) $ is also called the transfinite diameter of $ E $. If $ E $ is a finite set, then one has $ d ( E) = 0 $. The transfinite diameter $ d ( E) $, the Chebyshev constant $ \tau ( E) $ and the capacity $ C ( E) $ are equal:
$$ d ( E) = \tau ( E) = C ( E). $$
The transfinite diameter of a set $ E $ has the following properties: 1) if $ E _ {1} \subset E $, then $ d ( E _ {1} ) \leq d ( E) $; 2) if $ a $ is a fixed complex number and $ E _ {1} = \{ {w } : {w = az, z \in E } \} $, then $ d ( E _ {1} ) = | a | d ( E) $; 3) if $ E _ \epsilon $ is the set of points at a distance at most $ \epsilon $ from $ E $, then $ \lim\limits _ {\epsilon \rightarrow 0 } d ( E _ \epsilon ) = d ( E) $; 4) if $ E ^ {*} $ is the set of roots of the equation
$$ Q ( z) = z ^ {k} + a _ {1} z ^ {k - 1 } + \dots + a _ {k} = w, $$
where $ Q ( z) $ is a given polynomial and $ w $ runs through $ E $, then $ d ( E ^ {*} ) = \{ d ( E) \} ^ {1/k} $. The transfinite diameter of a circle is equal to its radius; the transfinite diameter of a line segment is equal to a quarter of its length.
Let $ E $ be a bounded continuum and let $ D $ be the component of the complement of $ E $ with respect to the extended plane that contains the point $ \infty $. Then the transfinite diameter of $ E $ is equal to the conformal radius of $ D $( with respect to $ \infty $; cf. Conformal radius of a domain).
The corresponding notions for sets in the hyperbolic and elliptic planes are defined as follows. Consider as a model of the hyperbolic plane the disc $ | z | < 1 $ with metric defined by the line element $ ds _ {h} = | dz |/( 1 - | z | ^ {2} ) $ and suppose that $ E $ is a closed infinite set in $ | z | < 1 $. Then the $ n $- th hyperbolic diameter $ d _ {n,h} ( E) $ of $ E $ is defined by (1) in which
$$ \tag{2 } [ a, b] = \ \left | \frac{a - b }{1 - \overline{a}\; b } \ \right | $$
is the hyperbolic pseudo-distance between $ a $ and $ b $, that is, $ [ a, b] = \mathop{\rm tanh} \rho _ {h} ( a, b) $, where $ \rho _ {h} ( a, b) $ is the hyperbolic distance between $ a $ and $ b $ in $ | z | < 1 $( see Hyperbolic metric). As in the Euclidean case, the sequence $ d _ {n,h} ( E) $ is non-increasing and the following limit exists:
$$ \lim\limits _ {n \rightarrow \infty } d _ {n,h} ( E) = d _ {h} ( E). $$
It is called the hyperbolic transfinite diameter of $ E $. Define the hyperbolic Chebyshev constant $ \tau _ {h} ( E) $ and the hyperbolic capacity $ C _ {h} ( E) $ of $ E $ via the hyperbolic pseudo-distance (2) between the points of $ | z | < 1 $ by analogy with the Chebyshev constant $ \tau ( E) $ and capacity $ C ( E) $ defined via the Euclidean distance between points of the $ z $- plane. Then one obtains
$$ d _ {h} ( E) = \tau _ {h} ( E) = C _ {h} ( E). $$
The hyperbolic transfinite diameter is invariant under the full group of hyperbolic isometries. If $ E $ is a continuum, then there is a simple relationship between the hyperbolic transfinite diameter $ d _ {n} ( E) $ and conformal mapping. Namely, let $ E $ be a continuum in the disc $ | z | < 1 $ such that the complement of $ E $ with respect to this disc is conformally equivalent to the annulus $ r < | w | < 1 $, $ 0 < r < 1 $. Then $ r = d _ {n} ( E) $.
Consider as a model of the elliptic plane the extended complex $ z $- plane with the metric of its Riemann sphere $ K $ of diameter 1, tangent to the $ z $- plane at the point $ z = 0 $, that is, the metric defined by the line element
$$ ds _ {e} = \ \frac{| dz | }{1 + | z | ^ {2} } ; $$
furthermore, let the points $ z $ and $ z ^ {*} = - 1/z $ be identified; these correspond to diametrically-opposite points of $ K $ under stereographic projection of the extended $ z $- plane onto $ K $. Let $ E $ be a closed infinite set in the extended $ z $- plane, $ E \cap E ^ {*} = \emptyset $, where $ E ^ {*} = \{ {- 1/z } : {z \in E } \} $. Then the $ n $- th elliptic diameter $ d _ {n,e} ( E) $ of $ E $ is defined by (1), in which
$$ \tag{3 } [ a, b] = \ \left | \frac{a - b }{1 + \overline{a}\; b } \ \right | $$
is the elliptic pseudo-distance between points $ a $ and $ b $ of $ E $, that is, $ [ a, b] = \mathop{\rm tan} \rho _ {e} ( a, b) $, where $ \rho _ {e} ( a, b) $( $ < \pi /2 $) is the elliptic distance between $ a $ and $ b $. As in the previous cases, the sequence $ d _ {n,e} ( E) $ is non-increasing and the following limit, called the elliptic transfinite diameter of $ E $, exists:
$$ \lim\limits _ {n \rightarrow \infty } d _ {n,e} ( E) = d _ {e} ( E). $$
Define the elliptic Chebyshev constant $ \tau _ {e} ( E) $ and the elliptic capacity $ C _ {e} ( E) $ of $ E $ via the elliptic pseudo-distance (3). Then one obtains:
$$ d _ {e} ( E) = \tau _ {e} ( E) = C _ {e} ( E). $$
The elliptic transfinite diameter $ d _ {e} ( E) $ is invariant under the group of fractional-linear transformations
$$ z \rightarrow \ \frac{pz + q }{- \overline{q}\; z + p } ,\ \ | p | ^ {2} + | q | ^ {2} = 1, $$
of the extended $ z $- plane onto itself, supplemented by the group of reflections in the elliptic lines. The first of these groups is isomorphic to the group of reflections of $ K $ about planes passing through its centre. With this definition the elliptic transfinite diameter of $ E $ is related to conformal mapping in the following way. If $ E $ is a continuum in the extended $ z $- plane, $ E \cap E ^ {*} = \emptyset $, and the complement of $ E \cup E ^ {*} $ with respect to the extended plane is conformally equivalent to the annulus $ r < | w | < 1/r $, $ 0 < r < 1 $, then $ r = d _ {e} ( E) $.
The notion of the transfinite diameter can be generalized to compacta $ E $ in a multi-dimensional Euclidean space $ \mathbf R ^ {m} $, $ m \geq 2 $, and is connected with potential theory. Let, for points $ x \in \mathbf R ^ {m} $,
$$ H (| x |) = \ \left \{ \begin{array}{ll} \mathop{\rm ln} { \frac{1}{| x | } } & \textrm{ for } m = 2, \\ { \frac{1}{| x | ^ {m - 2 } } } & \textrm{ for } m \geq 3, \\ \end{array} \right .$$
be a fundamental solution of the Laplace equation, and for the set of points $ ( x _ {j} ) _ {j = 1 } ^ {n} \subset E $, let
$$ \chi _ {n} ( E) = \ \inf \left \{ { { \frac{2}{n ( n - 1) } } \sum _ {\begin{array}{c} j, k = 1 \\ j < k \end{array} } ^ { n } H (| x _ {j} - x _ {k} |) } : { ( x _ {j} ) _ {j = 1 } ^ {n} \subset E } \right \} . $$
Then for $ m = 2 $ one has
$$ d ( E) = C ( E) = \ \mathop{\rm exp} \left ( - \lim\limits _ {n \rightarrow \infty } \chi _ {n} ( E) \right ) ; $$
while for $ m \geq 3 $ it is expedient (see [4]) to take
$$ d ( E) = C ( E) = \ { \frac{1}{\lim\limits _ {n \rightarrow \infty } \chi _ {n} ( E) } } . $$
References
| [1] | M. Fekete, "Ueber die Verteilung der Wurzeln bei gewissen algebraischen Gleichungen mit ganzzahligen Koeffizienten" Math. Z. , 17 (1923) pp. 228–249 |
| [2] | G. Pólya, G. Szegö, "Ueber den transfiniten Durchmesser (Kapazitätskonstante) von ebenen und räumlichen Punktmengen" J. Reine Angew. Math. , 165 (1931) pp. 4–49 |
| [3] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
| [4] | L. Carleson, "Selected problems on exceptional sets" , v. Nostrand (1967) |
| [5] | V.I. Smirnov, A.N. Lebedev, "Functions of a complex variable" , M.I.T. (1968) (Translated from Russian) |
| [6] | M. Tsuji, "Potential theory in modern function theory" , Chelsea, reprint (1959) |
| [7] | R. Kühnau, "Geometrie der konformen Abbildung auf der hyperbolischen und der elliptischen Ebene" , Deutsch. Verlag Wissenschaft. (1974) |
Comments
Outer radius is another term for transfinite diameter. See [a1] for a survey on connections between transfinite diameter, Robin constant and capacity in $ \mathbf R ^ {2} $ or $ \mathbf R ^ {n} $.
The notion of transfinite diameter also makes good sense in several complex variables, if interpreted in the correct way: (1) with $ [ a, b] = | a- b | $ is a root of a Vandermondian determinant:
$$ d _ {n} ( E) = ( \max _ {x ^ {( n ) } \in E ^ {n} } | V ( x ^ {(} n) ) | ) ^ {2/n( n- 1) } , $$
where
$$ V( x ^ {(} n) ) = \mathop{\rm det} [ x _ {i} ^ {j} ] _ {\begin{array} {c} i = 1 \dots n \\ j= 0 \dots n- 1 \end{array} } . $$
In $ \mathbf C ^ {n} $, let $ e _ {1} \dots e _ {m _ {n} } $ be an ordered system of monomials of degree $ \leq n $ and let $ x ^ {(} n) $ be a point in $ E ^ {m _ {n} } \subset \mathbf C ^ {m _ {n} } $. Then $ V ( x ^ {(} n) ) $ is defined as $ \mathop{\rm det} [ e _ {i} ( x _ {j} )] $, $ x ^ {n} = ( x _ {1} \dots x _ {m _ {n} } ) $, and $ d _ {n} ( E) = ( \max _ {x ^ {(} n) \in E ^ {m _ {n} } } V( x ^ {(} n) ) ) ^ {1/ \mathop{\rm deg} V( x ^ {n} ) } $. The related capacity is the one associated to the complex Monge–Ampère operator.
References
| [a1] | R.E. Kleinman, "On a unified characterization of capacity" J. Král (ed.) J. Lukeš (ed.) J. Veselý (ed.) , Potential theory. Survey and problems (Prague, 1987) , Lect. notes in math. , 1344 , Plenum (1988) pp. 103–120 |
| [a2] | M. Klimek, "Pluripotential theory" , Cambridge Univ. Press (1991) |
| [a3] | J. Siciak, "Extremal plurisubharmonic functions and capacities in 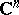 " , Sophia Kokyuroku in Math. , 14 , Dept. Math. Sophia Univ. Tokyo (1982) " , Sophia Kokyuroku in Math. , 14 , Dept. Math. Sophia Univ. Tokyo (1982) |
Transfinite diameter. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Transfinite_diameter&oldid=49634