Difference between revisions of "Order statistic"
Ulf Rehmann (talk | contribs) m (Undo revision 48066 by Ulf Rehmann (talk)) Tag: Undo |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | o0700701.png | ||
| + | $#A+1 = 125 n = 1 | ||
| + | $#C+1 = 125 : ~/encyclopedia/old_files/data/O070/O.0700070 Order statistic | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A member of the series of order statistics (also called [[Variational series|variational series]]) based on the results of observations. Let a random vector $ X = ( X _ {1} \dots X _ {n} ) $ | |
| + | be observed which assumes values $ x = ( x _ {1} \dots x _ {n} ) $ | ||
| + | in an $ n $- | ||
| + | dimensional Euclidean space $ \mathbf R ^ {n} $, | ||
| + | $ n \geq 2 $, | ||
| + | and let, further, a function $ \phi ( \cdot ) : \mathbf R ^ {n} \rightarrow \mathbf R ^ {n} $ | ||
| + | be given on $ \mathbf R ^ {n} $ | ||
| + | by the rule | ||
| − | + | $$ | |
| + | \phi ( x) = x ^ {( \cdot ) } ,\ \ | ||
| + | x \in \mathbf R ^ {n} , | ||
| + | $$ | ||
| − | + | where $ x ^ {( \cdot ) } = ( x _ {(} n1) \dots x _ {(} nn) ) $ | |
| + | is a vector in $ \mathbf R ^ {n} $ | ||
| + | obtained from $ x $ | ||
| + | by rearranging its coordinates $ x _ {1} \dots x _ {n} $ | ||
| + | in ascending order of magnitude, i.e. the components $ x _ {(} n1) \dots x _ {(} nn) $ | ||
| + | of the vector $ x ^ {( \cdot ) } $ | ||
| + | satisfy the relation | ||
| − | + | $$ \tag{1 } | |
| + | x _ {(} n1) \leq \dots \leq x _ {(} nn) . | ||
| + | $$ | ||
| − | + | In this case the statistic $ X ^ {( \cdot ) } = \phi ( X) = ( X _ {(} n1) \dots X _ {(} nn) ) $ | |
| + | is the series (or vector) of order statistics, and its $ k $- | ||
| + | th component $ X _ {nk} $( | ||
| + | $ k = 1 \dots n $) | ||
| + | is called the $ k $- | ||
| + | th order statistic. | ||
| + | |||
| + | In the theory of order statistics the best studied case is the one where the components $ X _ {1} \dots X _ {n} $ | ||
| + | of the random vector $ X $ | ||
| + | are independent random variables having the same distribution, as is assumed hereafter. If $ F ( u) $ | ||
| + | is the distribution function of the random variable $ X _ {i} $, | ||
| + | $ i = 1 \dots n $, | ||
| + | then the distribution function $ F _ {nk} ( u) $ | ||
| + | of the $ k $- | ||
| + | th order statistic $ X _ {(} nk) $ | ||
| + | is given by the formula | ||
| + | |||
| + | $$ \tag{2 } | ||
| + | F _ {nk} ( u) = {\mathsf P} \{ X _ {(} nk) \leq u \} = \ | ||
| + | I _ {F(} u) ( k , n - k + 1 ) , | ||
| + | $$ | ||
where | where | ||
| − | + | $$ | |
| + | I _ {y} ( a , b ) = | ||
| + | \frac{1}{B ( a , b ) } | ||
| + | |||
| + | \int\limits _ { 0 } ^ { y } x ^ {a-} 1 ( 1 - x ) ^ {b-} 1 dx | ||
| + | $$ | ||
| − | is the [[Incomplete beta-function|incomplete beta-function]]. From (2) it follows that if the distribution function | + | is the [[Incomplete beta-function|incomplete beta-function]]. From (2) it follows that if the distribution function $ F( u) $ |
| + | has probability density $ f ( u) $, | ||
| + | then the probability density $ f _ {nk} ( u) $ | ||
| + | of the $ k $- | ||
| + | th order statistic $ X _ {(} nk) $, | ||
| + | $ k = 1 \dots n $, | ||
| + | also exists and is given by the formula | ||
| − | + | $$ \tag{3 } | |
| + | f _ {nk} ( u) = n! over {( k - 1 ) ! ( n - k ) ! } | ||
| + | [ F ( u) ] ^ {k-} 1 [ 1 - F ( u) ] ^ {n-} k f ( u) , | ||
| + | $$ | ||
| − | < | + | $$ |
| + | - \infty < u < \infty . | ||
| + | $$ | ||
| − | Assuming the existence of the probability density | + | Assuming the existence of the probability density $ f ( u) $ |
| + | one obtains the joint probability density $ f _ {r _ {1} \dots r _ {k} } ( u _ {1} \dots u _ {k} ) $ | ||
| + | of the order statistics $ X _ {( nr _ {1} ) } \dots X _ {( nr _ {k} ) } $, | ||
| + | $ 1 \leq r _ {1} < \dots < r _ {k} \leq n $, | ||
| + | $ k \leq n $, | ||
| + | which is given by the formula | ||
| − | + | $$ \tag{4 } | |
| + | f _ {r _ {1} \dots r _ {k} } ( u _ {1} \dots u _ {k} ) = | ||
| + | $$ | ||
| − | + | $$ | |
| + | = \ | ||
| + | n! over {( r _ {1} - 1 ) ! ( r _ {2} - r _ {1} - 1 ) ! \dots ( n - r _ {k} ) ! } \times | ||
| + | $$ | ||
| − | + | $$ | |
| + | \times | ||
| + | F ^ { r _ {1} - 1 } ( u _ {1} ) f ( u _ {1} ) [ F ( u _ {2} ) - | ||
| + | F ( u _ {1} ) ] ^ {r _ {2} - r _ {1} - 1 } f ( u _ {2} ) \dots | ||
| + | $$ | ||
| − | + | $$ | |
| + | \dots [ 1 - F ( u _ {k} ) ] ^ {n - r _ {k} } f ( u _ {k} ) , | ||
| + | $$ | ||
| − | < | + | $$ |
| + | - \infty < u _ {1} < \dots < u _ {k} < \infty . | ||
| + | $$ | ||
The formulas (2)–(4) allow one, for instance, to find the distribution of the so-called extremal order statistics (or sample minimum and sample maximum) | The formulas (2)–(4) allow one, for instance, to find the distribution of the so-called extremal order statistics (or sample minimum and sample maximum) | ||
| − | + | $$ | |
| + | X _ {(} n1) = \min _ {1 \leq i \leq n } \ | ||
| + | ( X _ {1} \dots X _ {n} ) \ \textrm{ and } \ \ | ||
| + | X _ {(} nn) = \max _ {1 \leq i \leq n } \ | ||
| + | ( X _ {1} \dots X _ {n} ) , | ||
| + | $$ | ||
| + | |||
| + | and also the distribution of $ W _ {n} = X _ {(} nn) - X _ {(} n1) $, | ||
| + | called the range statistic (or sample range). For instance, if the distribution function $ F ( u) $ | ||
| + | is continuous, then the distribution of $ W _ {n} $ | ||
| + | is given by | ||
| − | + | $$ \tag{5 } | |
| + | {\mathsf P} \{ W _ {n} < w \} = n \int\limits _ {- \infty } ^ \infty | ||
| + | [ F ( u + w ) - F ( u) ] ^ {n-} 1 d F ( u) ,\ w \geq 0 . | ||
| + | $$ | ||
| − | + | Formulas (2)–(5) show that, as in the general theory of sampling methods, exact distributions of order statistics cannot be used to obtain statistical inferences if the distribution function $ F ( u) $ | |
| + | is unknown. It is precisely for this reason that asymptotic methods for the distribution functions of order statistics, as the dimension $ n $ | ||
| + | of the vector of observations tends to infinity, have been widely developed in the theory of order statistics. In the asymptotic theory of order statistics one studies the limit distributions of appropriately standardized sequences of order statistics $ \{ X _ {(} nk) \} $ | ||
| + | as $ n \rightarrow \infty $; | ||
| + | moreover, generally speaking, the order number $ k $ | ||
| + | can change as a function of $ n $. | ||
| + | If the order number $ k $ | ||
| + | changes as $ n $ | ||
| + | tends to infinity in such a way that the limit $ \lim\limits _ {n \rightarrow \infty } k / n $ | ||
| + | exists and is not equal to $ 0 $ | ||
| + | or to $ 1 $, | ||
| + | then the corresponding order statistics $ X _ {(} nk) $ | ||
| + | of the considered sequence $ \{ X _ {(} nk) \} $ | ||
| + | are called central or mean order statistics. If, however, $ \lim\limits _ {n \rightarrow \infty } k/n $ | ||
| + | is equal to $ 0 $ | ||
| + | or to $ 1 $, | ||
| + | then they are called extreme order statistics. | ||
| − | + | In mathematical statistics central order statistics are used to construct consistent sequences of estimators (cf. [[Consistent estimator|Consistent estimator]]) for quantiles (cf. [[Quantile|Quantile]]) of the unknown distribution $ F ( u) $ | |
| + | based on the realization of a random vector $ X $ | ||
| + | or, in other words, to estimate the function $ F ^ { - 1 } ( u) $. | ||
| + | For instance, let $ x _ {P} $ | ||
| + | be a quantile of level $ P $( | ||
| + | $ 0 < P < 1 $) | ||
| + | of the distribution function $ F ( u) $ | ||
| + | about which one knowns that its probability density $ f ( u) $ | ||
| + | is continuous and strictly positive in some neighbourhood of the point $ x _ {P} $. | ||
| + | In this case the sequence of central order statistics $ \{ X _ {(} nk) \} $ | ||
| + | with order numbers $ k = [ ( n+ 1) P + 0 ,5 ] $, | ||
| + | where $ [ a] $ | ||
| + | is the integer part of the real number $ a $, | ||
| + | is a sequence of consistent estimators for the quantiles $ x _ {P} $, | ||
| + | $ n \rightarrow \infty $. | ||
| + | Moreover, this sequence of order statistics $ \{ X _ {(} nk) \} $ | ||
| + | has an asymptotically normal distribution with parameters | ||
| − | + | $$ | |
| + | x _ {P} \ \textrm{ and } \ | ||
| + | \frac{P ( 1 - P ) }{f ^ { 2 } ( x _ {P} ) ( n + 1 ) } | ||
| + | , | ||
| + | $$ | ||
| − | + | i.e. for any real $ x $ | |
| − | + | $$ \tag{6 } | |
| + | \lim\limits _ {n \rightarrow \infty } {\mathsf P} \left \{ | ||
| − | + | \frac{X _ {(} nk) - x _ {P} }{\sqrt {P( 1 - P) / ( n + 1) } } | |
| + | f ( x _ {P} ) < x \right \} = \Phi ( x) , | ||
| + | $$ | ||
| − | where | + | where $ \Phi ( x) $ |
| + | is the standard normal distribution function. | ||
| − | Example 1. Let | + | Example 1. Let $ X ^ {( \cdot ) } = ( X _ {(} n1) \dots X _ {(} nn) ) $ |
| + | be a vector of order statistics based on a random vector $ X = ( X _ {1} \dots X _ {n} ) $. | ||
| + | The components of this vector are assumed to be independent random variables having the same probability distribution with a probability density that is continuous and positive in some neighbourhood of the median $ x _ {1/2} $. | ||
| + | In this case the sequence of sample medians $ \{ \mu _ {n} \} $, | ||
| + | defined for any $ n \geq 2 $ | ||
| + | by | ||
| − | + | $$ | |
| + | \mu _ {n} = \left \{ | ||
| + | \begin{array}{ll} | ||
| + | X _ {(} n,m+ 1) & \textrm{ for } n= 2m+ 1 \textrm{ odd } , \\ | ||
| − | + | \frac{1}{2} | |
| + | ( X _ {(} nm) + X _ {(} n,m+ 1) ) & \textrm{ for } n= 2m \textrm{ even } \\ | ||
| + | \end{array} | ||
| − | + | \right .$$ | |
| + | |||
| + | has an asymptotically normal distribution, as $ n \rightarrow \infty $, | ||
| + | with parameters | ||
| + | |||
| + | $$ | ||
| + | x _ {1/2} \ \textrm{ and } \ \{ 4 ( n+ 1) f ^ { 2 } ( x _ {1/2} ) \} ^ {-} 1 . | ||
| + | $$ | ||
In particular, if | In particular, if | ||
| − | + | $$ | |
| + | f ( x) = | ||
| + | \frac{1}{\sqrt {2 \pi \sigma }} | ||
| + | \mathop{\rm exp} | ||
| + | \left \{ - | ||
| + | \frac{( x - a ) ^ {2} }{2 \sigma ^ {2} } | ||
| + | \right \} ,\ \ | ||
| + | | a | \langle \infty ,\ \sigma \rangle 0 , | ||
| + | $$ | ||
| − | that is, | + | that is, $ X _ {i} $ |
| + | has the normal distribution $ N ( a , \sigma ^ {2} ) $, | ||
| + | then the sequence $ \{ \mu _ {n} \} $ | ||
| + | is asymptotically normally distributed with parameters $ x _ {1/2} = a $ | ||
| + | and $ \sigma ^ {2} \pi / ( 2 ( n+ 1) ) $. | ||
| + | If the sequence of statistics $ \{ \mu _ {n} \} $ | ||
| + | is compared with the sequence of best unbiased estimators (cf. [[Unbiased estimator|Unbiased estimator]]) | ||
| − | + | $$ | |
| + | \{ \overline{X}\; _ {n} \} ,\ \overline{X}\; _ {n} = | ||
| + | \frac{1}{n} | ||
| − | + | \sum _ { i= } 1 ^ { n } X _ {i} , | |
| + | $$ | ||
| − | + | for the mean $ a $ | |
| + | of the normal distribution, then one should prefer the sequence $ \{ \overline{X}\; _ {n} \} $, | ||
| + | since | ||
| − | + | $$ | |
| + | {\mathsf D} \overline{X}\; _ {n} = | ||
| + | \frac{\sigma ^ {2} }{n} | ||
| + | < \ | ||
| − | + | \frac{\sigma ^ {2} \pi }{2 ( n + 1 ) } | |
| + | \approx {\mathsf D} \mu _ {n} $$ | ||
| − | + | for any $ n \geq 2 $. | |
| − | + | Example 2. Let $ X ^ {( \cdot ) } = ( X _ {(} n1) \dots X _ {(} nn) ) $ | |
| + | be the vector of order statistics based on the random vector $ X = ( X _ {1} \dots X _ {n} ) $ | ||
| + | whose components are independent and uniformly distributed on an interval $ [ a - h , a + h ] $; | ||
| + | moreover, suppose that the parameters $ a $ | ||
| + | and $ h $ | ||
| + | are unknown. In this case the sequences $ \{ Y _ {n} \} $ | ||
| + | and $ \{ Z _ {n} \} $ | ||
| + | of statistics, where | ||
| − | + | $$ | |
| + | Y _ {n} = | ||
| + | \frac{1}{2} | ||
| + | ( X _ {(} n1) + X _ {(} nn) ) \ \textrm{ and } \ \ | ||
| + | Z _ {n} = n+ | ||
| + | \frac{1}{2(} | ||
| + | n- 1) ( X _ {(} nn) - X _ {(} n1) ), | ||
| + | $$ | ||
| − | + | $$ | |
| + | n \geq 2 , | ||
| + | $$ | ||
| − | One can show that the sequences | + | are consistent sequences of superefficient unbiased estimators (cf. [[Superefficient estimator|Superefficient estimator]]) for $ a $ |
| + | and $ h $, | ||
| + | respectively. Moreover, | ||
| + | |||
| + | $$ | ||
| + | {\mathsf D} Y _ {n} = | ||
| + | \frac{2 h ^ {2} }{( n+ 1) ( n+ 2) } | ||
| + | \ \textrm{ and } \ \ | ||
| + | {\mathsf D} Z _ {n} = | ||
| + | \frac{2 h ^ {2} }{( n- 1) ( n+ 2) } | ||
| + | . | ||
| + | $$ | ||
| + | |||
| + | One can show that the sequences $ \{ Y _ {n} \} $ | ||
| + | and $ \{ Z _ {n} \} $ | ||
| + | define the best estimators for $ a $ | ||
| + | and $ h $ | ||
| + | in the sense of the minimum of the square risk in the class of linear unbiased estimators expressed in terms of order statistics. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S.S. Wilks, "Mathematical statistics" , Princeton Univ. Press (1950)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> H.A. David, "Order statistics" , Wiley (1970)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> E.J. Gumble, "Statistics of extremes" , Columbia Univ. Press (1958)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> J. Hájek, Z. Sidák, "Theory of rank tests" , Acad. Press (1967)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> B.V. Gnedenko, "Limit theorems for the maximal term of a variational series" ''Dokl. Akad. Nauk SSSR'' , '''32''' : 1 (1941) pp. 7–9 (In Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> B.V. Gnedenko, "Sur la distribution limite du terme maximum d'une série aléatoire" ''Ann. of Math.'' , '''44''' : 3 (1943) pp. 423–453</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> N.V. Smirnov, "Limit distributions for the terms of a variational series" ''Trudy Mat. Inst. Steklov.'' , '''25''' (1949) pp. 5–59 (In Russian)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> N.V. Smirnov, "Some remarks on limit laws for order statistics" ''Theor. Probab. Appl.'' , '''12''' : 2 (1967) pp. 337–339 ''Teor. Veroyatnost. i Primenen.'' , '''12''' : 2 (1967) pp. 391–392</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> D.M. Chibisov, "On limit distributions for order statistics" ''Theor. Probab. Appl.'' , '''9''' : 1 (1964) pp. 142–148 ''Teor. Veroyatnost. Primenen.'' , '''9''' : 1 (1964) pp. 159–165</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> A.T. Craig, "On the distributions of certain statistics" ''Amer. J. Math.'' , '''54''' (1932) pp. 353–366</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> L.H.C. Tippett, "On the extreme individuals and the range of samples taken from a normal population" ''Biometrika'' , '''17''' (1925) pp. 364–387</TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> E.S. Pearson, "The percentage limits for the distribution of ranges in samples from a normal population (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070070/o070070127.png" />)" ''Biometrika'' , '''24''' (1932) pp. 404–417</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S.S. Wilks, "Mathematical statistics" , Princeton Univ. Press (1950)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> H.A. David, "Order statistics" , Wiley (1970)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> E.J. Gumble, "Statistics of extremes" , Columbia Univ. Press (1958)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> J. Hájek, Z. Sidák, "Theory of rank tests" , Acad. Press (1967)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> B.V. Gnedenko, "Limit theorems for the maximal term of a variational series" ''Dokl. Akad. Nauk SSSR'' , '''32''' : 1 (1941) pp. 7–9 (In Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> B.V. Gnedenko, "Sur la distribution limite du terme maximum d'une série aléatoire" ''Ann. of Math.'' , '''44''' : 3 (1943) pp. 423–453</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> N.V. Smirnov, "Limit distributions for the terms of a variational series" ''Trudy Mat. Inst. Steklov.'' , '''25''' (1949) pp. 5–59 (In Russian)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> N.V. Smirnov, "Some remarks on limit laws for order statistics" ''Theor. Probab. Appl.'' , '''12''' : 2 (1967) pp. 337–339 ''Teor. Veroyatnost. i Primenen.'' , '''12''' : 2 (1967) pp. 391–392</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> D.M. Chibisov, "On limit distributions for order statistics" ''Theor. Probab. Appl.'' , '''9''' : 1 (1964) pp. 142–148 ''Teor. Veroyatnost. Primenen.'' , '''9''' : 1 (1964) pp. 159–165</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> A.T. Craig, "On the distributions of certain statistics" ''Amer. J. Math.'' , '''54''' (1932) pp. 353–366</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> L.H.C. Tippett, "On the extreme individuals and the range of samples taken from a normal population" ''Biometrika'' , '''17''' (1925) pp. 364–387</TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> E.S. Pearson, "The percentage limits for the distribution of ranges in samples from a normal population (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070070/o070070127.png" />)" ''Biometrika'' , '''24''' (1932) pp. 404–417</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R.J. Serfling, "Approximation theorems of mathematical statistics" , Wiley (1980)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R.J. Serfling, "Approximation theorems of mathematical statistics" , Wiley (1980)</TD></TR></table> | ||
Revision as of 14:54, 7 June 2020
A member of the series of order statistics (also called variational series) based on the results of observations. Let a random vector $ X = ( X _ {1} \dots X _ {n} ) $
be observed which assumes values $ x = ( x _ {1} \dots x _ {n} ) $
in an $ n $-
dimensional Euclidean space $ \mathbf R ^ {n} $,
$ n \geq 2 $,
and let, further, a function $ \phi ( \cdot ) : \mathbf R ^ {n} \rightarrow \mathbf R ^ {n} $
be given on $ \mathbf R ^ {n} $
by the rule
$$ \phi ( x) = x ^ {( \cdot ) } ,\ \ x \in \mathbf R ^ {n} , $$
where $ x ^ {( \cdot ) } = ( x _ {(} n1) \dots x _ {(} nn) ) $ is a vector in $ \mathbf R ^ {n} $ obtained from $ x $ by rearranging its coordinates $ x _ {1} \dots x _ {n} $ in ascending order of magnitude, i.e. the components $ x _ {(} n1) \dots x _ {(} nn) $ of the vector $ x ^ {( \cdot ) } $ satisfy the relation
$$ \tag{1 } x _ {(} n1) \leq \dots \leq x _ {(} nn) . $$
In this case the statistic $ X ^ {( \cdot ) } = \phi ( X) = ( X _ {(} n1) \dots X _ {(} nn) ) $ is the series (or vector) of order statistics, and its $ k $- th component $ X _ {nk} $( $ k = 1 \dots n $) is called the $ k $- th order statistic.
In the theory of order statistics the best studied case is the one where the components $ X _ {1} \dots X _ {n} $ of the random vector $ X $ are independent random variables having the same distribution, as is assumed hereafter. If $ F ( u) $ is the distribution function of the random variable $ X _ {i} $, $ i = 1 \dots n $, then the distribution function $ F _ {nk} ( u) $ of the $ k $- th order statistic $ X _ {(} nk) $ is given by the formula
$$ \tag{2 } F _ {nk} ( u) = {\mathsf P} \{ X _ {(} nk) \leq u \} = \ I _ {F(} u) ( k , n - k + 1 ) , $$
where
$$ I _ {y} ( a , b ) = \frac{1}{B ( a , b ) } \int\limits _ { 0 } ^ { y } x ^ {a-} 1 ( 1 - x ) ^ {b-} 1 dx $$
is the incomplete beta-function. From (2) it follows that if the distribution function $ F( u) $ has probability density $ f ( u) $, then the probability density $ f _ {nk} ( u) $ of the $ k $- th order statistic $ X _ {(} nk) $, $ k = 1 \dots n $, also exists and is given by the formula
$$ \tag{3 } f _ {nk} ( u) = n! over {( k - 1 ) ! ( n - k ) ! } [ F ( u) ] ^ {k-} 1 [ 1 - F ( u) ] ^ {n-} k f ( u) , $$
$$ - \infty < u < \infty . $$
Assuming the existence of the probability density $ f ( u) $ one obtains the joint probability density $ f _ {r _ {1} \dots r _ {k} } ( u _ {1} \dots u _ {k} ) $ of the order statistics $ X _ {( nr _ {1} ) } \dots X _ {( nr _ {k} ) } $, $ 1 \leq r _ {1} < \dots < r _ {k} \leq n $, $ k \leq n $, which is given by the formula
$$ \tag{4 } f _ {r _ {1} \dots r _ {k} } ( u _ {1} \dots u _ {k} ) = $$
$$ = \ n! over {( r _ {1} - 1 ) ! ( r _ {2} - r _ {1} - 1 ) ! \dots ( n - r _ {k} ) ! } \times $$
$$ \times F ^ { r _ {1} - 1 } ( u _ {1} ) f ( u _ {1} ) [ F ( u _ {2} ) - F ( u _ {1} ) ] ^ {r _ {2} - r _ {1} - 1 } f ( u _ {2} ) \dots $$
$$ \dots [ 1 - F ( u _ {k} ) ] ^ {n - r _ {k} } f ( u _ {k} ) , $$
$$ - \infty < u _ {1} < \dots < u _ {k} < \infty . $$
The formulas (2)–(4) allow one, for instance, to find the distribution of the so-called extremal order statistics (or sample minimum and sample maximum)
$$ X _ {(} n1) = \min _ {1 \leq i \leq n } \ ( X _ {1} \dots X _ {n} ) \ \textrm{ and } \ \ X _ {(} nn) = \max _ {1 \leq i \leq n } \ ( X _ {1} \dots X _ {n} ) , $$
and also the distribution of $ W _ {n} = X _ {(} nn) - X _ {(} n1) $, called the range statistic (or sample range). For instance, if the distribution function $ F ( u) $ is continuous, then the distribution of $ W _ {n} $ is given by
$$ \tag{5 } {\mathsf P} \{ W _ {n} < w \} = n \int\limits _ {- \infty } ^ \infty [ F ( u + w ) - F ( u) ] ^ {n-} 1 d F ( u) ,\ w \geq 0 . $$
Formulas (2)–(5) show that, as in the general theory of sampling methods, exact distributions of order statistics cannot be used to obtain statistical inferences if the distribution function $ F ( u) $ is unknown. It is precisely for this reason that asymptotic methods for the distribution functions of order statistics, as the dimension $ n $ of the vector of observations tends to infinity, have been widely developed in the theory of order statistics. In the asymptotic theory of order statistics one studies the limit distributions of appropriately standardized sequences of order statistics $ \{ X _ {(} nk) \} $ as $ n \rightarrow \infty $; moreover, generally speaking, the order number $ k $ can change as a function of $ n $. If the order number $ k $ changes as $ n $ tends to infinity in such a way that the limit $ \lim\limits _ {n \rightarrow \infty } k / n $ exists and is not equal to $ 0 $ or to $ 1 $, then the corresponding order statistics $ X _ {(} nk) $ of the considered sequence $ \{ X _ {(} nk) \} $ are called central or mean order statistics. If, however, $ \lim\limits _ {n \rightarrow \infty } k/n $ is equal to $ 0 $ or to $ 1 $, then they are called extreme order statistics.
In mathematical statistics central order statistics are used to construct consistent sequences of estimators (cf. Consistent estimator) for quantiles (cf. Quantile) of the unknown distribution $ F ( u) $ based on the realization of a random vector $ X $ or, in other words, to estimate the function $ F ^ { - 1 } ( u) $. For instance, let $ x _ {P} $ be a quantile of level $ P $( $ 0 < P < 1 $) of the distribution function $ F ( u) $ about which one knowns that its probability density $ f ( u) $ is continuous and strictly positive in some neighbourhood of the point $ x _ {P} $. In this case the sequence of central order statistics $ \{ X _ {(} nk) \} $ with order numbers $ k = [ ( n+ 1) P + 0 ,5 ] $, where $ [ a] $ is the integer part of the real number $ a $, is a sequence of consistent estimators for the quantiles $ x _ {P} $, $ n \rightarrow \infty $. Moreover, this sequence of order statistics $ \{ X _ {(} nk) \} $ has an asymptotically normal distribution with parameters
$$ x _ {P} \ \textrm{ and } \ \frac{P ( 1 - P ) }{f ^ { 2 } ( x _ {P} ) ( n + 1 ) } , $$
i.e. for any real $ x $
$$ \tag{6 } \lim\limits _ {n \rightarrow \infty } {\mathsf P} \left \{ \frac{X _ {(} nk) - x _ {P} }{\sqrt {P( 1 - P) / ( n + 1) } } f ( x _ {P} ) < x \right \} = \Phi ( x) , $$
where $ \Phi ( x) $ is the standard normal distribution function.
Example 1. Let $ X ^ {( \cdot ) } = ( X _ {(} n1) \dots X _ {(} nn) ) $ be a vector of order statistics based on a random vector $ X = ( X _ {1} \dots X _ {n} ) $. The components of this vector are assumed to be independent random variables having the same probability distribution with a probability density that is continuous and positive in some neighbourhood of the median $ x _ {1/2} $. In this case the sequence of sample medians $ \{ \mu _ {n} \} $, defined for any $ n \geq 2 $ by
$$ \mu _ {n} = \left \{ \begin{array}{ll} X _ {(} n,m+ 1) & \textrm{ for } n= 2m+ 1 \textrm{ odd } , \\ \frac{1}{2} ( X _ {(} nm) + X _ {(} n,m+ 1) ) & \textrm{ for } n= 2m \textrm{ even } \\ \end{array} \right .$$
has an asymptotically normal distribution, as $ n \rightarrow \infty $, with parameters
$$ x _ {1/2} \ \textrm{ and } \ \{ 4 ( n+ 1) f ^ { 2 } ( x _ {1/2} ) \} ^ {-} 1 . $$
In particular, if
$$ f ( x) = \frac{1}{\sqrt {2 \pi \sigma }} \mathop{\rm exp} \left \{ - \frac{( x - a ) ^ {2} }{2 \sigma ^ {2} } \right \} ,\ \ | a | \langle \infty ,\ \sigma \rangle 0 , $$
that is, $ X _ {i} $ has the normal distribution $ N ( a , \sigma ^ {2} ) $, then the sequence $ \{ \mu _ {n} \} $ is asymptotically normally distributed with parameters $ x _ {1/2} = a $ and $ \sigma ^ {2} \pi / ( 2 ( n+ 1) ) $. If the sequence of statistics $ \{ \mu _ {n} \} $ is compared with the sequence of best unbiased estimators (cf. Unbiased estimator)
$$ \{ \overline{X}\; _ {n} \} ,\ \overline{X}\; _ {n} = \frac{1}{n} \sum _ { i= } 1 ^ { n } X _ {i} , $$
for the mean $ a $ of the normal distribution, then one should prefer the sequence $ \{ \overline{X}\; _ {n} \} $, since
$$ {\mathsf D} \overline{X}\; _ {n} = \frac{\sigma ^ {2} }{n} < \ \frac{\sigma ^ {2} \pi }{2 ( n + 1 ) } \approx {\mathsf D} \mu _ {n} $$
for any $ n \geq 2 $.
Example 2. Let $ X ^ {( \cdot ) } = ( X _ {(} n1) \dots X _ {(} nn) ) $ be the vector of order statistics based on the random vector $ X = ( X _ {1} \dots X _ {n} ) $ whose components are independent and uniformly distributed on an interval $ [ a - h , a + h ] $; moreover, suppose that the parameters $ a $ and $ h $ are unknown. In this case the sequences $ \{ Y _ {n} \} $ and $ \{ Z _ {n} \} $ of statistics, where
$$ Y _ {n} = \frac{1}{2} ( X _ {(} n1) + X _ {(} nn) ) \ \textrm{ and } \ \ Z _ {n} = n+ \frac{1}{2(} n- 1) ( X _ {(} nn) - X _ {(} n1) ), $$
$$ n \geq 2 , $$
are consistent sequences of superefficient unbiased estimators (cf. Superefficient estimator) for $ a $ and $ h $, respectively. Moreover,
$$ {\mathsf D} Y _ {n} = \frac{2 h ^ {2} }{( n+ 1) ( n+ 2) } \ \textrm{ and } \ \ {\mathsf D} Z _ {n} = \frac{2 h ^ {2} }{( n- 1) ( n+ 2) } . $$
One can show that the sequences $ \{ Y _ {n} \} $ and $ \{ Z _ {n} \} $ define the best estimators for $ a $ and $ h $ in the sense of the minimum of the square risk in the class of linear unbiased estimators expressed in terms of order statistics.
References
| [1] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) |
| [2] | S.S. Wilks, "Mathematical statistics" , Princeton Univ. Press (1950) |
| [3] | H.A. David, "Order statistics" , Wiley (1970) |
| [4] | E.J. Gumble, "Statistics of extremes" , Columbia Univ. Press (1958) |
| [5] | J. Hájek, Z. Sidák, "Theory of rank tests" , Acad. Press (1967) |
| [6] | B.V. Gnedenko, "Limit theorems for the maximal term of a variational series" Dokl. Akad. Nauk SSSR , 32 : 1 (1941) pp. 7–9 (In Russian) |
| [7] | B.V. Gnedenko, "Sur la distribution limite du terme maximum d'une série aléatoire" Ann. of Math. , 44 : 3 (1943) pp. 423–453 |
| [8] | N.V. Smirnov, "Limit distributions for the terms of a variational series" Trudy Mat. Inst. Steklov. , 25 (1949) pp. 5–59 (In Russian) |
| [9] | N.V. Smirnov, "Some remarks on limit laws for order statistics" Theor. Probab. Appl. , 12 : 2 (1967) pp. 337–339 Teor. Veroyatnost. i Primenen. , 12 : 2 (1967) pp. 391–392 |
| [10] | D.M. Chibisov, "On limit distributions for order statistics" Theor. Probab. Appl. , 9 : 1 (1964) pp. 142–148 Teor. Veroyatnost. Primenen. , 9 : 1 (1964) pp. 159–165 |
| [11] | A.T. Craig, "On the distributions of certain statistics" Amer. J. Math. , 54 (1932) pp. 353–366 |
| [12] | L.H.C. Tippett, "On the extreme individuals and the range of samples taken from a normal population" Biometrika , 17 (1925) pp. 364–387 |
| [13] | E.S. Pearson, "The percentage limits for the distribution of ranges in samples from a normal population (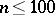 )" Biometrika , 24 (1932) pp. 404–417 )" Biometrika , 24 (1932) pp. 404–417 |
Comments
References
| [a1] | R.J. Serfling, "Approximation theorems of mathematical statistics" , Wiley (1980) |
Order statistic. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Order_statistic&oldid=49502