Difference between revisions of "Modular curve"
Ulf Rehmann (talk | contribs) m (Undo revision 47869 by Ulf Rehmann (talk)) Tag: Undo |
Ulf Rehmann (talk | contribs) m (Undo revision 49302 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | m0644101.png | ||
| + | $#A+1 = 69 n = 1 | ||
| + | $#C+1 = 69 : ~/encyclopedia/old_files/data/M064/M.0604410 Modular curve | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A complete [[Algebraic curve|algebraic curve]] $ X _ {\widetilde \Gamma } $ | |
| + | uniformized by a subgroup $ \widetilde \Gamma $ | ||
| + | of finite index in the [[Modular group|modular group]] $ \Gamma $; | ||
| + | more precisely, a modular curve is a complete algebraic curve obtained from a quotient space $ H / \widetilde \Gamma $, | ||
| + | where $ H $ | ||
| + | is the upper half-plane, together with a finite number of parabolic points (the equivalence classes relative to $ \widetilde \Gamma $ | ||
| + | of the rational points of the boundary of $ H $). | ||
| + | The best known examples of subgroups $ \widetilde \Gamma $ | ||
| + | of finite index in $ \Gamma $ | ||
| + | are the congruence subgroups containing a principal congruence subgroup $ \Gamma ( N) $ | ||
| + | of level $ N $ | ||
| + | for some integer $ N > 1 $, | ||
| + | represented by the matrices | ||
| − | + | $$ | |
| + | A \in \mathop{\rm SL} _ {2} ( \mathbf Z ) ,\ \ | ||
| + | A \equiv \ | ||
| + | \left ( | ||
| − | + | (see [[Modular group|Modular group]]). The least such $ N $ | |
| + | is called the level of the subgroup $ \widetilde \Gamma $. | ||
| + | In particular, the subgroup $ \Gamma _ {0} ( N) $ | ||
| + | represented by matrices which are congruent $ \mathop{\rm mod} N $ | ||
| + | to upper-triangular matrices has level $ N $. | ||
| + | Corresponding to each subgroup $ \widetilde \Gamma $ | ||
| + | of finite index there is a covering of the modular curve $ X _ {\widetilde \Gamma } \rightarrow X _ \Gamma $, | ||
| + | which ramifies only over the images of the points $ z = i $, | ||
| + | $ z = ( 1 + i \sqrt 3 ) / 2 $, | ||
| + | $ z = \infty $. | ||
| + | For a congruence subgroup $ \widetilde \Gamma $ | ||
| + | the ramification of this covering allows one to determine the genus of $ X _ {\widetilde \Gamma } $ | ||
| + | and to prove the existence of subgroups $ \widetilde \Gamma $ | ||
| + | of finite index in $ \Gamma $ | ||
| + | which are not congruence subgroups (see [[#References|[4]]], Vol. 2, [[#References|[2]]]). The genus of $ X _ {\Gamma ( N) } $ | ||
| + | is $ 0 $ | ||
| + | for $ N \leq 2 $ | ||
| + | and equals | ||
| − | + | $$ | |
| + | 1 + | ||
| − | + | \frac{N ^ {2} ( N - 6 ) }{24} | |
| − | + | \prod _ {p \mid N } | |
| + | ( 1 - p ^ {-} 2 ) , | ||
| + | $$ | ||
| − | The investigation of the geometry and arithmetic of modular curves is based on the use of groups of automorphisms of the projective limit of the curves | + | $ p $ |
| + | a prime number, for $ N > 2 $. | ||
| + | A modular curve is always defined over an algebraic number field (usually over $ \mathbf Q $ | ||
| + | or a cyclic extension of it). The rational functions on a modular curve lift to modular functions (of a higher level) and form a field; the automorphisms of this field have been studied (see [[#References|[2]]]). A holomorphic differential form on a modular curve $ X _ {\widetilde \Gamma } $ | ||
| + | is given on $ H $ | ||
| + | by a differential $ f ( z) d z $( | ||
| + | where $ f ( z) $ | ||
| + | is a holomorphic function) which is invariant under the transformations $ z \rightarrow \gamma ( z) $ | ||
| + | of $ \widetilde \Gamma $; | ||
| + | here $ f ( z) $ | ||
| + | is a cusp form of weight 2 relative to $ \widetilde \Gamma $. | ||
| + | The [[Zeta-function|zeta-function]] of a modular curve is a product of the Mellin transforms (cf. [[Mellin transform|Mellin transform]]) of modular forms and, consequently, has a meromorphic continuation and satisfies a functional equation. This fact serves as the point of departure for the Langlands–Weil theory on the relationship between modular forms and Dirichlet series (see [[#References|[7]]], [[#References|[8]]]). In particular, there is a hypothesis that each [[Elliptic curve|elliptic curve]] over $ \mathbf Q $( | ||
| + | with conductor $ N $) | ||
| + | can be uniformized by modular functions of level $ N $. | ||
| + | The homology of a modular curve is connected with modular symbols, which allows one to investigate the arithmetic of the values of the zeta-function of a modular curve in the centre of the critical strip and to construct the $ p $- | ||
| + | adic zeta-function of a modular curve (see [[#References|[1]]]). | ||
| + | |||
| + | A modular curve parametrizes a family of elliptic curves, being their moduli variety (see [[#References|[7]]], Vol. 2). In particular, for $ \widetilde \Gamma = \Gamma ( N) $ | ||
| + | a point $ z $ | ||
| + | of $ H / \Gamma ( N) $ | ||
| + | is in one-to-one correspondence with a pair consisting of an elliptic curve $ E _ {z} $( | ||
| + | analytically equivalent to a complex torus $ \mathbf C / ( \mathbf Z + \mathbf Z z) $) | ||
| + | and a point of order $ N $ | ||
| + | on $ E _ {z} $( | ||
| + | the image of $ z / N $). | ||
| + | |||
| + | Over each modular curve $ X _ {\widetilde \Gamma } $ | ||
| + | there is a natural algebraic fibre bundle $ E _ {\widetilde \Gamma } \rightarrow X _ {\widetilde \Gamma } $ | ||
| + | of elliptic curves if $ \widetilde \Gamma $ | ||
| + | does not contain $ - 1 $, | ||
| + | compactified by degenerate curves above the parabolic points of $ X _ {\widetilde \Gamma } $. | ||
| + | Powers $ E _ {down 2 {\widetilde \Gamma } } ^ {( w) } $, | ||
| + | where $ w \geq 1 $ | ||
| + | is an integer, are called Kuga varieties (see [[#References|[3]]], [[#References|[5]]]). The zeta- functions of $ E _ {down 2 {\widetilde \Gamma } } ^ {( w) } $ | ||
| + | are related to the Mellin transforms of modular forms, and their homology to the periods of modular forms (see [[#References|[3]]], [[#References|[7]]]). | ||
| + | |||
| + | The rational points on a modular curve correspond to elliptic curves having rational points of finite order (or rational subgroups of points); their description (see [[#References|[6]]]) made it possible to solve the problem of determining the possible torsion subgroups of elliptic curves over $ \mathbf Q $. | ||
| + | |||
| + | The investigation of the geometry and arithmetic of modular curves is based on the use of groups of automorphisms of the projective limit of the curves $ X _ {\widetilde \Gamma } $ | ||
| + | with respect to decreasing $ \widetilde \Gamma $, | ||
| + | which (in essence) coincides with the group $ \mathop{\rm SL} _ {2} ( A) $ | ||
| + | over the ring $ A $ | ||
| + | of rational adèles. On each modular curve $ X _ {\widetilde \Gamma } $ | ||
| + | this gives a non-trivial ring of correspondences $ R _ {\widetilde \Gamma } $( | ||
| + | a Hecke ring), which has applications in the theory of modular forms (cf. [[Modular form|Modular form]], [[#References|[3]]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> Yu.I. Manin, "Parabolic points and zeta-functions of modular curves" ''Math. USSR Izv.'' , '''6''' : 1 (1972) pp. 19–64 ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''36''' : 1 (1972) pp. 19–66</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> G. Shimura, "Introduction to the arithmetic theory of automorphic functions" , Math. Soc. Japan (1971)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> V.V. [V.V. Shokurov] Šokurov, "Holomorphic differential forms of higher degree on Kuga's modular varieties" ''Math. USSR Sb.'' , '''30''' : 1 (1976) pp. 119–142 ''Mat. Sb.'' , '''101''' : 1 (1976) pp. 131–157</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> F. Klein, R. Fricke, "Vorlesungen über die Theorie der elliptischen Modulfunktionen" , '''1–2''' , Teubner (1890–1892)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> M. Kuga, G. Shimura, "On the zeta function of a fibre variety whose fibres are abelian varieties" ''Ann. of Math.'' , '''82''' (1965) pp. 478–539</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> B. Mazur, J.-P. Serre, "Points rationnels des courbes modulaires <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441070.png" /> (d'après A. Ogg)" , ''Sem. Bourbaki 1974/1975'' , ''Lect. notes in math.'' , '''514''' , Springer (1976) pp. 238–255</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> J.-P. Serre (ed.) P. Deligne (ed.) W. Kuyk (ed.) , ''Modular functions of one variable. 1–6'' , ''Lect. notes in math.'' , '''320; 349; 350; 476; 601; 627''' , Springer (1973–1977)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> A. Weil, "Ueber die Bestimmung Dirichletscher Reihen durch Funktionalgleichungen" ''Math. Ann.'' , '''168''' (1967) pp. 149–156</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> Yu.I. Manin, "Parabolic points and zeta-functions of modular curves" ''Math. USSR Izv.'' , '''6''' : 1 (1972) pp. 19–64 ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''36''' : 1 (1972) pp. 19–66</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> G. Shimura, "Introduction to the arithmetic theory of automorphic functions" , Math. Soc. Japan (1971)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> V.V. [V.V. Shokurov] Šokurov, "Holomorphic differential forms of higher degree on Kuga's modular varieties" ''Math. USSR Sb.'' , '''30''' : 1 (1976) pp. 119–142 ''Mat. Sb.'' , '''101''' : 1 (1976) pp. 131–157</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> F. Klein, R. Fricke, "Vorlesungen über die Theorie der elliptischen Modulfunktionen" , '''1–2''' , Teubner (1890–1892)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> M. Kuga, G. Shimura, "On the zeta function of a fibre variety whose fibres are abelian varieties" ''Ann. of Math.'' , '''82''' (1965) pp. 478–539</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> B. Mazur, J.-P. Serre, "Points rationnels des courbes modulaires <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064410/m06441070.png" /> (d'après A. Ogg)" , ''Sem. Bourbaki 1974/1975'' , ''Lect. notes in math.'' , '''514''' , Springer (1976) pp. 238–255</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> J.-P. Serre (ed.) P. Deligne (ed.) W. Kuyk (ed.) , ''Modular functions of one variable. 1–6'' , ''Lect. notes in math.'' , '''320; 349; 350; 476; 601; 627''' , Springer (1973–1977)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> A. Weil, "Ueber die Bestimmung Dirichletscher Reihen durch Funktionalgleichungen" ''Math. Ann.'' , '''168''' (1967) pp. 149–156</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> N.M. Katz, B. Mazur, "Arithmetic moduli of elliptic curves" , Princeton Univ. Press (1985)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> N.M. Katz, B. Mazur, "Arithmetic moduli of elliptic curves" , Princeton Univ. Press (1985)</TD></TR></table> | ||
Revision as of 13:58, 7 June 2020
A complete algebraic curve $ X _ {\widetilde \Gamma } $
uniformized by a subgroup $ \widetilde \Gamma $
of finite index in the modular group $ \Gamma $;
more precisely, a modular curve is a complete algebraic curve obtained from a quotient space $ H / \widetilde \Gamma $,
where $ H $
is the upper half-plane, together with a finite number of parabolic points (the equivalence classes relative to $ \widetilde \Gamma $
of the rational points of the boundary of $ H $).
The best known examples of subgroups $ \widetilde \Gamma $
of finite index in $ \Gamma $
are the congruence subgroups containing a principal congruence subgroup $ \Gamma ( N) $
of level $ N $
for some integer $ N > 1 $,
represented by the matrices
$$ A \in \mathop{\rm SL} _ {2} ( \mathbf Z ) ,\ \ A \equiv \ \left ( (see [[Modular group|Modular group]]). The least such $ N $ is called the level of the subgroup $ \widetilde \Gamma $. In particular, the subgroup $ \Gamma _ {0} ( N) $ represented by matrices which are congruent $ \mathop{\rm mod} N $ to upper-triangular matrices has level $ N $. Corresponding to each subgroup $ \widetilde \Gamma $ of finite index there is a covering of the modular curve $ X _ {\widetilde \Gamma } \rightarrow X _ \Gamma $, which ramifies only over the images of the points $ z = i $, $ z = ( 1 + i \sqrt 3 ) / 2 $, $ z = \infty $. For a congruence subgroup $ \widetilde \Gamma $ the ramification of this covering allows one to determine the genus of $ X _ {\widetilde \Gamma } $ and to prove the existence of subgroups $ \widetilde \Gamma $ of finite index in $ \Gamma $ which are not congruence subgroups (see [[#References|[4]]], Vol. 2, [[#References|[2]]]). The genus of $ X _ {\Gamma ( N) } $ is $ 0 $ for $ N \leq 2 $ and equals $$ 1 +
\frac{N ^ {2} ( N - 6 ) }{24}
\prod _ {p \mid N } ( 1 - p ^ {-} 2 ) , $$
$ p $ a prime number, for $ N > 2 $. A modular curve is always defined over an algebraic number field (usually over $ \mathbf Q $ or a cyclic extension of it). The rational functions on a modular curve lift to modular functions (of a higher level) and form a field; the automorphisms of this field have been studied (see [2]). A holomorphic differential form on a modular curve $ X _ {\widetilde \Gamma } $ is given on $ H $ by a differential $ f ( z) d z $( where $ f ( z) $ is a holomorphic function) which is invariant under the transformations $ z \rightarrow \gamma ( z) $ of $ \widetilde \Gamma $; here $ f ( z) $ is a cusp form of weight 2 relative to $ \widetilde \Gamma $. The zeta-function of a modular curve is a product of the Mellin transforms (cf. Mellin transform) of modular forms and, consequently, has a meromorphic continuation and satisfies a functional equation. This fact serves as the point of departure for the Langlands–Weil theory on the relationship between modular forms and Dirichlet series (see [7], [8]). In particular, there is a hypothesis that each elliptic curve over $ \mathbf Q $( with conductor $ N $) can be uniformized by modular functions of level $ N $. The homology of a modular curve is connected with modular symbols, which allows one to investigate the arithmetic of the values of the zeta-function of a modular curve in the centre of the critical strip and to construct the $ p $- adic zeta-function of a modular curve (see [1]).
A modular curve parametrizes a family of elliptic curves, being their moduli variety (see [7], Vol. 2). In particular, for $ \widetilde \Gamma = \Gamma ( N) $ a point $ z $ of $ H / \Gamma ( N) $ is in one-to-one correspondence with a pair consisting of an elliptic curve $ E _ {z} $( analytically equivalent to a complex torus $ \mathbf C / ( \mathbf Z + \mathbf Z z) $) and a point of order $ N $ on $ E _ {z} $( the image of $ z / N $).
Over each modular curve $ X _ {\widetilde \Gamma } $ there is a natural algebraic fibre bundle $ E _ {\widetilde \Gamma } \rightarrow X _ {\widetilde \Gamma } $ of elliptic curves if $ \widetilde \Gamma $ does not contain $ - 1 $, compactified by degenerate curves above the parabolic points of $ X _ {\widetilde \Gamma } $. Powers $ E _ {down 2 {\widetilde \Gamma } } ^ {( w) } $, where $ w \geq 1 $ is an integer, are called Kuga varieties (see [3], [5]). The zeta- functions of $ E _ {down 2 {\widetilde \Gamma } } ^ {( w) } $ are related to the Mellin transforms of modular forms, and their homology to the periods of modular forms (see [3], [7]).
The rational points on a modular curve correspond to elliptic curves having rational points of finite order (or rational subgroups of points); their description (see [6]) made it possible to solve the problem of determining the possible torsion subgroups of elliptic curves over $ \mathbf Q $.
The investigation of the geometry and arithmetic of modular curves is based on the use of groups of automorphisms of the projective limit of the curves $ X _ {\widetilde \Gamma } $ with respect to decreasing $ \widetilde \Gamma $, which (in essence) coincides with the group $ \mathop{\rm SL} _ {2} ( A) $ over the ring $ A $ of rational adèles. On each modular curve $ X _ {\widetilde \Gamma } $ this gives a non-trivial ring of correspondences $ R _ {\widetilde \Gamma } $( a Hecke ring), which has applications in the theory of modular forms (cf. Modular form, [3]).
References
| [1] | Yu.I. Manin, "Parabolic points and zeta-functions of modular curves" Math. USSR Izv. , 6 : 1 (1972) pp. 19–64 Izv. Akad. Nauk SSSR Ser. Mat. , 36 : 1 (1972) pp. 19–66 |
| [2] | G. Shimura, "Introduction to the arithmetic theory of automorphic functions" , Math. Soc. Japan (1971) |
| [3] | V.V. [V.V. Shokurov] Šokurov, "Holomorphic differential forms of higher degree on Kuga's modular varieties" Math. USSR Sb. , 30 : 1 (1976) pp. 119–142 Mat. Sb. , 101 : 1 (1976) pp. 131–157 |
| [4] | F. Klein, R. Fricke, "Vorlesungen über die Theorie der elliptischen Modulfunktionen" , 1–2 , Teubner (1890–1892) |
| [5] | M. Kuga, G. Shimura, "On the zeta function of a fibre variety whose fibres are abelian varieties" Ann. of Math. , 82 (1965) pp. 478–539 |
| [6] | B. Mazur, J.-P. Serre, "Points rationnels des courbes modulaires 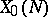 (d'après A. Ogg)" , Sem. Bourbaki 1974/1975 , Lect. notes in math. , 514 , Springer (1976) pp. 238–255 (d'après A. Ogg)" , Sem. Bourbaki 1974/1975 , Lect. notes in math. , 514 , Springer (1976) pp. 238–255 |
| [7] | J.-P. Serre (ed.) P. Deligne (ed.) W. Kuyk (ed.) , Modular functions of one variable. 1–6 , Lect. notes in math. , 320; 349; 350; 476; 601; 627 , Springer (1973–1977) |
| [8] | A. Weil, "Ueber die Bestimmung Dirichletscher Reihen durch Funktionalgleichungen" Math. Ann. , 168 (1967) pp. 149–156 |
Comments
References
| [a1] | N.M. Katz, B. Mazur, "Arithmetic moduli of elliptic curves" , Princeton Univ. Press (1985) |
Modular curve. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Modular_curve&oldid=49307