Difference between revisions of "Variation-parametric method"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | v0961801.png | ||
| + | $#A+1 = 44 n = 4 | ||
| + | $#C+1 = 44 : ~/encyclopedia/old_files/data/V096/V.0906180 Variation\AAhparametric method | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A method which is a synthesis of Goluzin's method of variations (cf. [[Internal variations, method of|Internal variations, method of]]) and Loewner's [[Parametric representation method|parametric representation method]] for the important subclass of univalent functions of class $ S $ | |
| + | mapping the disc $ E = \{ {z } : {| z | < 1 } \} $ | ||
| + | onto domains obtained from the plane $ \mathbf C _ {w} $ | ||
| + | by cutting along piecewise-continuous arcs. This synthesis is obtained by a special variation which, in the simplest case of one Jordan cut, is determined by the following theorem. Let the function $ w = f ( z) \in S $ | ||
| + | map $ E $ | ||
| + | onto the domain $ B( 0) $ | ||
| + | obtained from $ {\overline{\mathbf C}\; } _ {w} $ | ||
| + | by performing the cut | ||
| − | + | $$ | |
| + | L = \{ {w } : {w = \phi ( t), 0 \leq t \leq \infty } \} | ||
| + | ,\ \ | ||
| + | \phi ( \infty ) = \infty , | ||
| + | $$ | ||
| − | + | where $ \phi ( t) $ | |
| + | is continuous, while the domain $ B( \tau ) = {\overline{\mathbf C}\; } _ {w} \setminus L ( \tau ) $, | ||
| + | where $ L( \tau ) = \{ {w } : {w = \phi ( t), 0 \leq \tau \leq t \leq \infty } \} $, | ||
| + | is simply connected. A parametrization of the cut $ L $ | ||
| + | may be considered such that the function $ z = F( w, \tau ) $, | ||
| + | $ F( 0, \tau ) = 0 $, | ||
| + | associated to $ f( z) $, | ||
| + | which univalently and conformally maps $ B( \tau ) $ | ||
| + | onto $ E $, | ||
| + | is normalized by the condition $ F _ {w} ^ { \prime } ( 0, \tau ) = e ^ {- \tau } $. | ||
| + | Let $ \Psi ( z, \tau ) $ | ||
| + | denote the function inverse to $ F( w, \tau ) $ | ||
| + | for a fixed $ \tau $. | ||
| + | Then, for all points $ z _ {k} \in E $, | ||
| + | ( $ k = 1 \dots n $; | ||
| + | $ n = 1, 2 ,\dots $) | ||
| + | and for all constants $ A _ {k} $, | ||
| + | there exists a function $ f _ {*} ( z) $ | ||
| + | in $ S $ | ||
| + | which may be represented in the form | ||
| − | + | $$ | |
| + | f _ {*} ( z) = f ( z) + | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | + | ||
| + | \lambda \sum _ {k = 1 } ^ { n } \left [ 2A _ {k} H ^ {2} ( z _ {k} , | ||
| + | \tau ) | ||
| + | \frac{f ^ {2} ( z) }{f ( z) - \Psi ( z _ {k} , \tau ) } | ||
| + | \right . + | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | + \left . | ||
| + | A _ {k} K ( z, \tau , z _ {k} ) + A | ||
| + | bar _ {k} K \left ( z, \tau , | ||
| + | \frac{1}{\overline{z}\; _ {k} } | ||
| + | \right ) \right ] + \gamma ( \lambda , E). | ||
| + | $$ | ||
Here | Here | ||
| − | + | $$ | |
| + | K ( z, \tau , \zeta ) = \ | ||
| + | |||
| + | \frac{F ( f ( z), \tau ) }{F _ {w} ^ { \prime } ( f ( z), \tau ) } | ||
| + | \cdot | ||
| − | + | \frac{\zeta + F ( f ( z), \tau ) }{\zeta - F ( f ( z), \tau ) } | |
| + | - f ( z), | ||
| + | $$ | ||
| − | + | $$ | |
| + | H ( z, \tau ) = | ||
| + | \frac{z \Psi _ {z} ^ \prime ( z, \tau ) }{\Psi ( z, \tau ) } | ||
| + | , | ||
| + | $$ | ||
| − | + | and $ \gamma ( \lambda , E) $ | |
| + | is a holomorphic function in $ E $, | ||
| + | the limit of which with respect to $ \lambda $ | ||
| + | uniformly tends to zero inside $ E $ | ||
| + | as $ \lambda \rightarrow 0 $( | ||
| + | $ \lambda > 0 $). | ||
| − | + | If, in the course of study of extremal problems in $ S $, | |
| + | use is made of the special variation mentioned above and of Loewner's equation | ||
| − | + | $$ | |
| − | which is satisfied by a function | + | \frac{d \zeta }{d \tau } |
| + | = \ | ||
| + | - \zeta | ||
| + | \frac{\mu ( \tau ) + \zeta }{\mu ( \tau ) - \zeta } | ||
| + | , | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | \mu ( \tau ) = \Psi ( \phi ( \tau ), \tau ), | ||
| + | $$ | ||
| + | |||
| + | which is satisfied by a function $ F( w, \tau ) $ | ||
| + | subject to the condition $ F( f( z), 0) = z $, | ||
| + | two equations are usually obtained for the function which was associated to the extremal function. Irrespective of the constants contained in the equations, which can be expressed as values of the extremal function, further study of these equations frequently yields complete solutions of the problems under consideration, in particular in the problem of the domain of values of a functional which depends analytically on the function, its derivative and their conjugate values in $ S $. | ||
| + | The method was proposed by P.P. Kufarev [[#References|[1]]]; for subsequent development and applications of the method see [[#References|[2]]]–[[#References|[5]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> P.P. Kufarev, "On one property of extremal domains of coefficient problems" ''Dokl. Akad. Nauk SSSR'' , '''97''' : 3 (1954) pp. 391–393 (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I.A. Aleksandrov, ''Uchen. Zap. Tomsk. Univ.'' , '''32''' (1958) pp. 41–57</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I.A. Aleksandrov, "Boundary values of the functional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096180/v09618045.png" /> on the class of holomorphic univalent functions in the disc" ''Sibirsk. Mat. Zh.'' , '''4''' : 1 (1963) pp. 17–31 (In Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> M.I. Red'kov, "The domains of values of the functional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096180/v09618046.png" /> for certain classes of bounded univalent functions" ''Soviet Math. Dokl.'' , '''1''' : 2 (1960) pp. 848–851 ''Dokl. Akad. Nauk SSSR'' , '''133''' : 2 (1960) pp. 284–287</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> M.I. Red'kov, "The domain of values of the functional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096180/v09618047.png" /> on the class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096180/v09618048.png" />" ''Izv. Vyssh. Uchebn. Zaved. Mat.'' , '''4(29)''' (1962) pp. 134–142 (In Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> P.P. Kufarev, "On one property of extremal domains of coefficient problems" ''Dokl. Akad. Nauk SSSR'' , '''97''' : 3 (1954) pp. 391–393 (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I.A. Aleksandrov, ''Uchen. Zap. Tomsk. Univ.'' , '''32''' (1958) pp. 41–57</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I.A. Aleksandrov, "Boundary values of the functional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096180/v09618045.png" /> on the class of holomorphic univalent functions in the disc" ''Sibirsk. Mat. Zh.'' , '''4''' : 1 (1963) pp. 17–31 (In Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> M.I. Red'kov, "The domains of values of the functional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096180/v09618046.png" /> for certain classes of bounded univalent functions" ''Soviet Math. Dokl.'' , '''1''' : 2 (1960) pp. 848–851 ''Dokl. Akad. Nauk SSSR'' , '''133''' : 2 (1960) pp. 284–287</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> M.I. Red'kov, "The domain of values of the functional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096180/v09618047.png" /> on the class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096180/v09618048.png" />" ''Izv. Vyssh. Uchebn. Zaved. Mat.'' , '''4(29)''' (1962) pp. 134–142 (In Russian)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
Latest revision as of 08:27, 6 June 2020
A method which is a synthesis of Goluzin's method of variations (cf. Internal variations, method of) and Loewner's parametric representation method for the important subclass of univalent functions of class $ S $
mapping the disc $ E = \{ {z } : {| z | < 1 } \} $
onto domains obtained from the plane $ \mathbf C _ {w} $
by cutting along piecewise-continuous arcs. This synthesis is obtained by a special variation which, in the simplest case of one Jordan cut, is determined by the following theorem. Let the function $ w = f ( z) \in S $
map $ E $
onto the domain $ B( 0) $
obtained from $ {\overline{\mathbf C}\; } _ {w} $
by performing the cut
$$ L = \{ {w } : {w = \phi ( t), 0 \leq t \leq \infty } \} ,\ \ \phi ( \infty ) = \infty , $$
where $ \phi ( t) $ is continuous, while the domain $ B( \tau ) = {\overline{\mathbf C}\; } _ {w} \setminus L ( \tau ) $, where $ L( \tau ) = \{ {w } : {w = \phi ( t), 0 \leq \tau \leq t \leq \infty } \} $, is simply connected. A parametrization of the cut $ L $ may be considered such that the function $ z = F( w, \tau ) $, $ F( 0, \tau ) = 0 $, associated to $ f( z) $, which univalently and conformally maps $ B( \tau ) $ onto $ E $, is normalized by the condition $ F _ {w} ^ { \prime } ( 0, \tau ) = e ^ {- \tau } $. Let $ \Psi ( z, \tau ) $ denote the function inverse to $ F( w, \tau ) $ for a fixed $ \tau $. Then, for all points $ z _ {k} \in E $, ( $ k = 1 \dots n $; $ n = 1, 2 ,\dots $) and for all constants $ A _ {k} $, there exists a function $ f _ {*} ( z) $ in $ S $ which may be represented in the form
$$ f _ {*} ( z) = f ( z) + $$
$$ + \lambda \sum _ {k = 1 } ^ { n } \left [ 2A _ {k} H ^ {2} ( z _ {k} , \tau ) \frac{f ^ {2} ( z) }{f ( z) - \Psi ( z _ {k} , \tau ) } \right . + $$
$$ + \left . A _ {k} K ( z, \tau , z _ {k} ) + A bar _ {k} K \left ( z, \tau , \frac{1}{\overline{z}\; _ {k} } \right ) \right ] + \gamma ( \lambda , E). $$
Here
$$ K ( z, \tau , \zeta ) = \ \frac{F ( f ( z), \tau ) }{F _ {w} ^ { \prime } ( f ( z), \tau ) } \cdot \frac{\zeta + F ( f ( z), \tau ) }{\zeta - F ( f ( z), \tau ) } - f ( z), $$
$$ H ( z, \tau ) = \frac{z \Psi _ {z} ^ \prime ( z, \tau ) }{\Psi ( z, \tau ) } , $$
and $ \gamma ( \lambda , E) $ is a holomorphic function in $ E $, the limit of which with respect to $ \lambda $ uniformly tends to zero inside $ E $ as $ \lambda \rightarrow 0 $( $ \lambda > 0 $).
If, in the course of study of extremal problems in $ S $, use is made of the special variation mentioned above and of Loewner's equation
$$ \frac{d \zeta }{d \tau } = \ - \zeta \frac{\mu ( \tau ) + \zeta }{\mu ( \tau ) - \zeta } , $$
$$ \mu ( \tau ) = \Psi ( \phi ( \tau ), \tau ), $$
which is satisfied by a function $ F( w, \tau ) $ subject to the condition $ F( f( z), 0) = z $, two equations are usually obtained for the function which was associated to the extremal function. Irrespective of the constants contained in the equations, which can be expressed as values of the extremal function, further study of these equations frequently yields complete solutions of the problems under consideration, in particular in the problem of the domain of values of a functional which depends analytically on the function, its derivative and their conjugate values in $ S $. The method was proposed by P.P. Kufarev [1]; for subsequent development and applications of the method see [2]–[5].
References
| [1] | P.P. Kufarev, "On one property of extremal domains of coefficient problems" Dokl. Akad. Nauk SSSR , 97 : 3 (1954) pp. 391–393 (In Russian) |
| [2] | I.A. Aleksandrov, Uchen. Zap. Tomsk. Univ. , 32 (1958) pp. 41–57 |
| [3] | I.A. Aleksandrov, "Boundary values of the functional 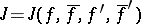 on the class of holomorphic univalent functions in the disc" Sibirsk. Mat. Zh. , 4 : 1 (1963) pp. 17–31 (In Russian) on the class of holomorphic univalent functions in the disc" Sibirsk. Mat. Zh. , 4 : 1 (1963) pp. 17–31 (In Russian) |
| [4] | M.I. Red'kov, "The domains of values of the functional 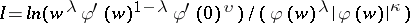 for certain classes of bounded univalent functions" Soviet Math. Dokl. , 1 : 2 (1960) pp. 848–851 Dokl. Akad. Nauk SSSR , 133 : 2 (1960) pp. 284–287 for certain classes of bounded univalent functions" Soviet Math. Dokl. , 1 : 2 (1960) pp. 848–851 Dokl. Akad. Nauk SSSR , 133 : 2 (1960) pp. 284–287 |
| [5] | M.I. Red'kov, "The domain of values of the functional 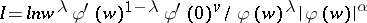 on the class on the class 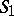 " Izv. Vyssh. Uchebn. Zaved. Mat. , 4(29) (1962) pp. 134–142 (In Russian) " Izv. Vyssh. Uchebn. Zaved. Mat. , 4(29) (1962) pp. 134–142 (In Russian) |
Comments
The idea to combine variational methods and Loewner theory seems to go back to M. Schiffer, cf. [a2], Chapts. 10, 11; see [a2], also for further references.
References
| [a1] | I.A. Aleksandrov, "Parametric extensions in the theory of univalent functions" , Moscow (1976) (In Russian) |
| [a2] | P.L. Duren, "Univalent functions" , Springer (1983) pp. Sect. 10.11 |
Variation-parametric method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Variation-parametric_method&oldid=49112