Difference between revisions of "Uniqueness properties of analytic functions"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | u0954301.png | ||
| + | $#A+1 = 127 n = 3 | ||
| + | $#C+1 = 127 : ~/encyclopedia/old_files/data/U095/U.0905430 Uniqueness properties of analytic functions | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
Properties of analytic functions that say that they are completely determined by their values on certain subsets of their domain of definition, or of its boundary; in this connection one may distinguish interior uniqueness properties and boundary uniqueness properties. | Properties of analytic functions that say that they are completely determined by their values on certain subsets of their domain of definition, or of its boundary; in this connection one may distinguish interior uniqueness properties and boundary uniqueness properties. | ||
==Interior uniqueness properties.== | ==Interior uniqueness properties.== | ||
| − | Let | + | Let $ D $ |
| + | be a domain in the complex plane $ \mathbf C = \mathbf C ^ {1} $. | ||
| + | The classical interior uniqueness theorem for holomorphic (that is, single-valued analytic) functions on $ D $ | ||
| + | states that if two holomorphic functions $ f ( z) $ | ||
| + | and $ g ( z) $ | ||
| + | in $ D $ | ||
| + | coincide on some set $ E \subset D $ | ||
| + | containing at least one limit point in $ D $, | ||
| + | then $ f ( z) \equiv g ( z) $ | ||
| + | everywhere in $ D $. | ||
| + | In other words, if a holomorphic function $ f ( z) $ | ||
| + | in $ D $ | ||
| + | vanishes on a set $ E \subset D $ | ||
| + | having at least one limit point in $ D $, | ||
| + | then $ f ( z) \equiv 0 $. | ||
| + | The proof of this interior uniqueness property of analytic functions shows that it is essentially a uniqueness property of power series in one complex variable $ z $. | ||
| + | The uniqueness property remains valid for meromorphic functions $ f ( z) $ | ||
| + | and $ g ( z) $ | ||
| + | in $ D $ | ||
| + | if one regards the poles of $ f ( z) $ | ||
| + | and $ g ( z) $ | ||
| + | as points at which the functions take the value $ \infty $. | ||
| − | In particular, if two analytic functions | + | In particular, if two analytic functions $ f ( z) $ |
| + | and $ g ( z) $ | ||
| + | coincide in an arbitrarily small neighbourhood of some point or on an arbitrarily small arc of some continuous curve, then $ f ( z) \equiv g ( z) $. | ||
| + | Another corollary: The set of $ A $- | ||
| + | points of an analytic function $ f ( z) $, | ||
| + | that is, the set of points $ z $ | ||
| + | at which $ f ( z) = A $, | ||
| + | cannot have limit points inside the domain of definition $ D $, | ||
| + | provided that $ f ( z) \not\equiv A $. | ||
| − | Two complete analytic functions in the sense of Weierstrass (cf. [[Complete analytic function|Complete analytic function]]) | + | Two complete analytic functions in the sense of Weierstrass (cf. [[Complete analytic function|Complete analytic function]]) $ F ( z) $, |
| + | $ G ( z) $ | ||
| + | are, in general, multiple valued, and have the following interior uniqueness property: Let $ f ( z) $, | ||
| + | $ g ( z) $ | ||
| + | be single-valued elements, or branches, of $ F ( z) $ | ||
| + | and $ G ( z) $, | ||
| + | defined on domains $ D _ {1} $ | ||
| + | and $ D _ {2} $, | ||
| + | respectively, with $ D _ {1} \cap D _ {2} \neq \emptyset $. | ||
| + | If $ f ( z) $ | ||
| + | and $ g ( z) $ | ||
| + | coincide on some set $ E \subset D _ {1} \cap D _ {2} $ | ||
| + | having at least one limit point $ z _ {0} \in D _ {1} \cap D _ {2} $, | ||
| + | then $ F ( z) $ | ||
| + | and $ G ( z) $ | ||
| + | have the same domain of existence and coincide everywhere as complete analytic functions. | ||
| − | These formulations of uniqueness properties do not carry over to the case of functions | + | These formulations of uniqueness properties do not carry over to the case of functions $ f ( z) $ |
| + | of several complex variables $ z = ( z _ {1} \dots z _ {n} ) $, | ||
| + | $ n > 1 $. | ||
| + | For example, the analytic function $ f ( z) = z _ {1} z _ {2} $ | ||
| + | is not identically zero, but vanishes on the analytic planes $ z _ {1} = 0 $ | ||
| + | and $ z _ {2} = 0 $ | ||
| + | of complex dimension $ n - 1 $. | ||
| + | The following uniqueness properties hold for such functions: | ||
| − | 1) If | + | 1) If $ f ( z) $ |
| + | is an analytic function on a domain $ D $ | ||
| + | of the complex space $ \mathbf C ^ {n} $ | ||
| + | and vanishes at all points of some non-empty open subset $ U \subset D $, | ||
| + | then $ f ( z) \equiv 0 $ | ||
| + | on $ D $. | ||
| − | 2) If | + | 2) If $ f ( z) $ |
| + | is an analytic function on a domain $ D \subset \mathbf C ^ {n} $ | ||
| + | that vanishes at some point $ z ^ {0} \in D $ | ||
| + | together with all its partial derivatives $ \partial ^ {k} f / \partial z _ {1} ^ {k _ {1} } \dots \partial z _ {n} ^ {k _ {n} } $, | ||
| + | $ k = k _ {1} + \dots + k _ {n} $; | ||
| + | $ k _ {j} = 0 , 1 ,\dots $; | ||
| + | $ j = 1 \dots n $, | ||
| + | then $ f ( z) \equiv 0 $ | ||
| + | on $ D $. | ||
| − | 3) If | + | 3) If $ f ( z) $ |
| + | is an analytic function on a domain $ D \subset \mathbf C ^ {n} $ | ||
| + | that vanishes in a real neighbourhood $ U _ \partial $ | ||
| + | of a point $ z ^ {0} = x ^ {0} + iy ^ {0} \in D $, | ||
| + | that is, on a set $ U _ \partial = \{ {z = x + iy \in \mathbf C ^ {n} } : {| x - x ^ {0} | < r, y = y ^ {0} } \} $, | ||
| + | then $ f ( z) \equiv 0 $ | ||
| + | on $ D $. | ||
| − | The difference between interior uniqueness properties in the cases | + | The difference between interior uniqueness properties in the cases $ n = 1 $ |
| + | and $ n > 1 $ | ||
| + | is caused by the different behaviour of power series in one and in several variables. | ||
==Boundary uniqueness properties.== | ==Boundary uniqueness properties.== | ||
| − | The uniqueness theorem stated above for an analytic function | + | The uniqueness theorem stated above for an analytic function $ f ( z) $ |
| + | of a single complex variable admits several generalizations to the case when the zeros of $ f ( z) $ | ||
| + | do not lie in the interior of the domain $ D $ | ||
| + | of analyticity, but on its boundary $ \Gamma $. | ||
| + | The most general and deepest boundary uniqueness theorems were obtained by N.N. Luzin and I.I. Privalov in 1925 (cf. also [[Luzin–Privalov theorems|Luzin–Privalov theorems]]). Let $ D $ | ||
| + | be a domain in the $ z $- | ||
| + | plane bounded by a rectifiable curve $ \Gamma $, | ||
| + | and let $ f ( z) $ | ||
| + | be a meromorphic function in $ D $. | ||
| + | Let $ \zeta _ {0} $ | ||
| + | be a point of $ \Gamma $ | ||
| + | at which the tangent to $ \Gamma $ | ||
| + | exists; almost-all points of a rectifiable curve have this property. One says that $ f ( z) $ | ||
| + | has an angular boundary value $ A $ | ||
| + | at $ \zeta _ {0} $ | ||
| + | if $ f ( z) $ | ||
| + | tends to $ A $ | ||
| + | as $ z $ | ||
| + | tends to $ \zeta _ {0} $ | ||
| + | remaining within the intersection of the domain $ D $ | ||
| + | and the interior of any angle less than $ \pi $ | ||
| + | with vertex $ \zeta _ {0} $ | ||
| + | having the normal to $ \Gamma $ | ||
| + | at $ \zeta _ {0} $ | ||
| + | as its bisector. | ||
| − | The Luzin–Privalov boundary uniqueness theorem for angular boundary values then holds: If | + | The Luzin–Privalov boundary uniqueness theorem for angular boundary values then holds: If $ f ( z) $ |
| + | is meromorphic in a domain $ D $ | ||
| + | bounded by a rectifiable curve $ \Gamma $ | ||
| + | and takes angular boundary values zero on a set $ E \subset \Gamma $ | ||
| + | of positive Lebesgue measure, then $ f ( z) \equiv 0 $. | ||
| + | In general, a meromorphic function need not have boundary values on $ \Gamma $. | ||
| + | But for a fairly large class of meromorphic functions, for example, for functions of bounded characteristic, the existence of angular boundary values almost everywhere on $ \Gamma $ | ||
| + | has been established. | ||
| − | Along with these, there are examples of bounded analytic functions in the unit disc | + | Along with these, there are examples of bounded analytic functions in the unit disc $ D $ |
| + | that converge to zero in all senses on a given set of points $ E $ | ||
| + | of measure zero on the unit circle $ \Gamma $. | ||
| + | Moreover, Luzin and Privalov have also constructed examples of analytic functions in the unit disc $ D $ | ||
| + | having zero radial boundary values, that is, tending to zero along radii, everywhere on a set $ E \subset \Gamma $ | ||
| + | of full measure $ 2 \pi $. | ||
| + | It turns out that in uniqueness problems the concept of the Baire category of a set is also very important. In fact, there is a Luzin–Privalov boundary uniqueness theorem for radial boundary values: If the function $ f ( z) $ | ||
| + | is meromorphic in the unit disc $ D $, | ||
| + | has radial boundary values zero on a set $ E $ | ||
| + | situated on an arc $ \sigma $ | ||
| + | of the unit circle $ \Gamma $, | ||
| + | and if $ E $ | ||
| + | is metrically dense and of the second Baire category in $ \sigma $, | ||
| + | then $ f ( z) \equiv 0 $. | ||
| + | (A set $ E $ | ||
| + | is called metrically dense in $ \sigma $ | ||
| + | if the intersection of $ E $ | ||
| + | with each subarc of $ \sigma $ | ||
| + | has positive measure.) | ||
See also [[Boundary properties of analytic functions|Boundary properties of analytic functions]]; [[Limit set|Limit set]]. | See also [[Boundary properties of analytic functions|Boundary properties of analytic functions]]; [[Limit set|Limit set]]. | ||
| Line 31: | Line 164: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.I. Markushevich, "Theory of functions of a complex variable" , '''1''' , Chelsea (1977) pp. Chapt. 3 (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> B.V. Shabat, "Introduction of complex analysis" , '''1–2''' , Moscow (1976) pp. Chapt. 2 (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> W. Rudin, "Function theory in the polydisc" , Benjamin (1969)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> G.M. [G.M. Khenkin] Henkin, E.M. [E.M. Chirka] Čirka, "Boundary properties of holomorphic functions of several complex variables" ''J. Soviet Math.'' , '''5''' (1976) pp. 612–687 ''Itogi Nauk. Sovrem. Probl. Mat.'' , '''4''' (1975) pp. 13–142</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> W. Rudin, "Function theory in the unit ball in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095430/u095430128.png" />" , Springer (1980)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> P. Koosis, "Introduction to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095430/u095430129.png" />-spaces. With an appendix on Wolff's proof of the corona theorem" , Cambridge Univ. Press (1980)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.I. Markushevich, "Theory of functions of a complex variable" , '''1''' , Chelsea (1977) pp. Chapt. 3 (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> B.V. Shabat, "Introduction of complex analysis" , '''1–2''' , Moscow (1976) pp. Chapt. 2 (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> W. Rudin, "Function theory in the polydisc" , Benjamin (1969)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> G.M. [G.M. Khenkin] Henkin, E.M. [E.M. Chirka] Čirka, "Boundary properties of holomorphic functions of several complex variables" ''J. Soviet Math.'' , '''5''' (1976) pp. 612–687 ''Itogi Nauk. Sovrem. Probl. Mat.'' , '''4''' (1975) pp. 13–142</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> W. Rudin, "Function theory in the unit ball in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095430/u095430128.png" />" , Springer (1980)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> P. Koosis, "Introduction to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095430/u095430129.png" />-spaces. With an appendix on Wolff's proof of the corona theorem" , Cambridge Univ. Press (1980)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | Analogues of the Luzin–Privalov examples of holomorphic functions, not identically equal to zero and with radial boundary values zero almost everywhere, have been found for the unit ball in | + | Analogues of the Luzin–Privalov examples of holomorphic functions, not identically equal to zero and with radial boundary values zero almost everywhere, have been found for the unit ball in $ \mathbf C ^ {n} $ |
| + | too, see [[#References|[a1]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> M. Hakim, N. Sibony, "Boundary properties of holomorphic functions in the ball in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095430/u095430131.png" />" ''Math. Ann.'' , '''276''' (1987) pp. 549–555</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> M. Hakim, N. Sibony, "Boundary properties of holomorphic functions in the ball in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095430/u095430131.png" />" ''Math. Ann.'' , '''276''' (1987) pp. 549–555</TD></TR></table> | ||
Latest revision as of 08:27, 6 June 2020
Properties of analytic functions that say that they are completely determined by their values on certain subsets of their domain of definition, or of its boundary; in this connection one may distinguish interior uniqueness properties and boundary uniqueness properties.
Interior uniqueness properties.
Let $ D $ be a domain in the complex plane $ \mathbf C = \mathbf C ^ {1} $. The classical interior uniqueness theorem for holomorphic (that is, single-valued analytic) functions on $ D $ states that if two holomorphic functions $ f ( z) $ and $ g ( z) $ in $ D $ coincide on some set $ E \subset D $ containing at least one limit point in $ D $, then $ f ( z) \equiv g ( z) $ everywhere in $ D $. In other words, if a holomorphic function $ f ( z) $ in $ D $ vanishes on a set $ E \subset D $ having at least one limit point in $ D $, then $ f ( z) \equiv 0 $. The proof of this interior uniqueness property of analytic functions shows that it is essentially a uniqueness property of power series in one complex variable $ z $. The uniqueness property remains valid for meromorphic functions $ f ( z) $ and $ g ( z) $ in $ D $ if one regards the poles of $ f ( z) $ and $ g ( z) $ as points at which the functions take the value $ \infty $.
In particular, if two analytic functions $ f ( z) $ and $ g ( z) $ coincide in an arbitrarily small neighbourhood of some point or on an arbitrarily small arc of some continuous curve, then $ f ( z) \equiv g ( z) $. Another corollary: The set of $ A $- points of an analytic function $ f ( z) $, that is, the set of points $ z $ at which $ f ( z) = A $, cannot have limit points inside the domain of definition $ D $, provided that $ f ( z) \not\equiv A $.
Two complete analytic functions in the sense of Weierstrass (cf. Complete analytic function) $ F ( z) $, $ G ( z) $ are, in general, multiple valued, and have the following interior uniqueness property: Let $ f ( z) $, $ g ( z) $ be single-valued elements, or branches, of $ F ( z) $ and $ G ( z) $, defined on domains $ D _ {1} $ and $ D _ {2} $, respectively, with $ D _ {1} \cap D _ {2} \neq \emptyset $. If $ f ( z) $ and $ g ( z) $ coincide on some set $ E \subset D _ {1} \cap D _ {2} $ having at least one limit point $ z _ {0} \in D _ {1} \cap D _ {2} $, then $ F ( z) $ and $ G ( z) $ have the same domain of existence and coincide everywhere as complete analytic functions.
These formulations of uniqueness properties do not carry over to the case of functions $ f ( z) $ of several complex variables $ z = ( z _ {1} \dots z _ {n} ) $, $ n > 1 $. For example, the analytic function $ f ( z) = z _ {1} z _ {2} $ is not identically zero, but vanishes on the analytic planes $ z _ {1} = 0 $ and $ z _ {2} = 0 $ of complex dimension $ n - 1 $. The following uniqueness properties hold for such functions:
1) If $ f ( z) $ is an analytic function on a domain $ D $ of the complex space $ \mathbf C ^ {n} $ and vanishes at all points of some non-empty open subset $ U \subset D $, then $ f ( z) \equiv 0 $ on $ D $.
2) If $ f ( z) $ is an analytic function on a domain $ D \subset \mathbf C ^ {n} $ that vanishes at some point $ z ^ {0} \in D $ together with all its partial derivatives $ \partial ^ {k} f / \partial z _ {1} ^ {k _ {1} } \dots \partial z _ {n} ^ {k _ {n} } $, $ k = k _ {1} + \dots + k _ {n} $; $ k _ {j} = 0 , 1 ,\dots $; $ j = 1 \dots n $, then $ f ( z) \equiv 0 $ on $ D $.
3) If $ f ( z) $ is an analytic function on a domain $ D \subset \mathbf C ^ {n} $ that vanishes in a real neighbourhood $ U _ \partial $ of a point $ z ^ {0} = x ^ {0} + iy ^ {0} \in D $, that is, on a set $ U _ \partial = \{ {z = x + iy \in \mathbf C ^ {n} } : {| x - x ^ {0} | < r, y = y ^ {0} } \} $, then $ f ( z) \equiv 0 $ on $ D $.
The difference between interior uniqueness properties in the cases $ n = 1 $ and $ n > 1 $ is caused by the different behaviour of power series in one and in several variables.
Boundary uniqueness properties.
The uniqueness theorem stated above for an analytic function $ f ( z) $ of a single complex variable admits several generalizations to the case when the zeros of $ f ( z) $ do not lie in the interior of the domain $ D $ of analyticity, but on its boundary $ \Gamma $. The most general and deepest boundary uniqueness theorems were obtained by N.N. Luzin and I.I. Privalov in 1925 (cf. also Luzin–Privalov theorems). Let $ D $ be a domain in the $ z $- plane bounded by a rectifiable curve $ \Gamma $, and let $ f ( z) $ be a meromorphic function in $ D $. Let $ \zeta _ {0} $ be a point of $ \Gamma $ at which the tangent to $ \Gamma $ exists; almost-all points of a rectifiable curve have this property. One says that $ f ( z) $ has an angular boundary value $ A $ at $ \zeta _ {0} $ if $ f ( z) $ tends to $ A $ as $ z $ tends to $ \zeta _ {0} $ remaining within the intersection of the domain $ D $ and the interior of any angle less than $ \pi $ with vertex $ \zeta _ {0} $ having the normal to $ \Gamma $ at $ \zeta _ {0} $ as its bisector.
The Luzin–Privalov boundary uniqueness theorem for angular boundary values then holds: If $ f ( z) $ is meromorphic in a domain $ D $ bounded by a rectifiable curve $ \Gamma $ and takes angular boundary values zero on a set $ E \subset \Gamma $ of positive Lebesgue measure, then $ f ( z) \equiv 0 $. In general, a meromorphic function need not have boundary values on $ \Gamma $. But for a fairly large class of meromorphic functions, for example, for functions of bounded characteristic, the existence of angular boundary values almost everywhere on $ \Gamma $ has been established.
Along with these, there are examples of bounded analytic functions in the unit disc $ D $ that converge to zero in all senses on a given set of points $ E $ of measure zero on the unit circle $ \Gamma $. Moreover, Luzin and Privalov have also constructed examples of analytic functions in the unit disc $ D $ having zero radial boundary values, that is, tending to zero along radii, everywhere on a set $ E \subset \Gamma $ of full measure $ 2 \pi $. It turns out that in uniqueness problems the concept of the Baire category of a set is also very important. In fact, there is a Luzin–Privalov boundary uniqueness theorem for radial boundary values: If the function $ f ( z) $ is meromorphic in the unit disc $ D $, has radial boundary values zero on a set $ E $ situated on an arc $ \sigma $ of the unit circle $ \Gamma $, and if $ E $ is metrically dense and of the second Baire category in $ \sigma $, then $ f ( z) \equiv 0 $. (A set $ E $ is called metrically dense in $ \sigma $ if the intersection of $ E $ with each subarc of $ \sigma $ has positive measure.)
See also Boundary properties of analytic functions; Limit set.
The investigation of boundary uniqueness properties of analytic functions of several complex variables has not yet achieved the same degree of completeness as for functions of a single variable (see [5], [6]).
References
| [1] | A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) pp. Chapt. 3 (Translated from Russian) |
| [2] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) pp. Chapt. 2 (In Russian) |
| [3] | I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
| [4] | E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) |
| [5] | W. Rudin, "Function theory in the polydisc" , Benjamin (1969) |
| [6] | G.M. [G.M. Khenkin] Henkin, E.M. [E.M. Chirka] Čirka, "Boundary properties of holomorphic functions of several complex variables" J. Soviet Math. , 5 (1976) pp. 612–687 Itogi Nauk. Sovrem. Probl. Mat. , 4 (1975) pp. 13–142 |
| [7] | W. Rudin, "Function theory in the unit ball in 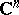 " , Springer (1980) " , Springer (1980) |
| [8] | P. Koosis, "Introduction to 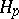 -spaces. With an appendix on Wolff's proof of the corona theorem" , Cambridge Univ. Press (1980) -spaces. With an appendix on Wolff's proof of the corona theorem" , Cambridge Univ. Press (1980) |
Comments
Analogues of the Luzin–Privalov examples of holomorphic functions, not identically equal to zero and with radial boundary values zero almost everywhere, have been found for the unit ball in $ \mathbf C ^ {n} $ too, see [a1].
References
| [a1] | M. Hakim, N. Sibony, "Boundary properties of holomorphic functions in the ball in 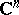 " Math. Ann. , 276 (1987) pp. 549–555 " Math. Ann. , 276 (1987) pp. 549–555 |
Uniqueness properties of analytic functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Uniqueness_properties_of_analytic_functions&oldid=49082