Difference between revisions of "Stickelberger ideal"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | s1102801.png | ||
| + | $#A+1 = 92 n = 2 | ||
| + | $#C+1 = 92 : ~/encyclopedia/old_files/data/S110/S.1100280 Stickelberger ideal | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | Let $ m $ | |
| + | be a fixed natural number and $ K _ {m} $ | ||
| + | the [[Cyclotomic field|cyclotomic field]] generated by a primitive $ m $ | ||
| + | th root of unity over the rational number field $ \mathbf Q $. | ||
| + | Let $ G \simeq ( \mathbf Z/m \mathbf Z ) ^ \times $ | ||
| + | be its [[Galois group|Galois group]] and $ \mathbf Z [ G ] $ | ||
| + | the group ring of $ G $( | ||
| + | cf. also [[Group algebra|Group algebra]]; [[Cross product|Cross product]]) over the rational integers $ \mathbf Z $. | ||
| + | They act on ideals and on the ideal class group $ C $ | ||
| + | of $ K _ {m} $( | ||
| + | cf. [[Class field theory|Class field theory]]). The Stickelberger ideal $ S $ | ||
| + | is an ideal in $ \mathbf Z [ G ] $ | ||
| + | annihilating $ C $ | ||
| + | and related with the relative class number $ h ^ {-} $ | ||
| + | of $ K _ {m} $. | ||
| + | It is defined as follows. | ||
| − | + | Let $ O $ | |
| + | be the ring of integers of $ K _ {m} $ | ||
| + | and $ \mathfrak p $ | ||
| + | a [[Prime ideal|prime ideal]] of $ O $ | ||
| + | that is prime to $ m $. | ||
| + | Let $ p $ | ||
| + | be a prime integer satisfying $ ( p ) = \mathfrak p \cap \mathbf Z $ | ||
| + | and let $ \mathbf F _ {p} = \mathbf Z/p \mathbf Z $ | ||
| + | be the [[Prime field|prime field]]. Define a mapping $ {\psi _ {0} } : {\mathbf F _ {p} } \rightarrow {\mathbf C ^ \times = \mathbf C \setminus \{ 0 \} } $ | ||
| + | by | ||
| − | + | $$ | |
| + | \psi _ {0} ( a ) = { \mathop{\rm exp} } \left ( { | ||
| + | \frac{2 \pi i }{p} | ||
| + | } a \right ) , | ||
| + | $$ | ||
| − | + | where $ \mathbf C $ | |
| + | is the complex number field. Let $ F = O/ \mathfrak p $ | ||
| + | be the residue field and define $ {\psi _ {\mathfrak p} } : F \rightarrow {\mathbf C ^ \times } $ | ||
| + | by composition of $ \psi _ {0} $ | ||
| + | and the trace mapping $ T : F \rightarrow {\mathbf F _ {p} } $, | ||
| + | i.e., $ \psi _ {\mathfrak p} = \psi _ {0} \circ T $. | ||
| + | Let $ W _ {m} $ | ||
| + | be the group of unities in $ K _ {m} $. | ||
| + | Then there is an injection | ||
| − | + | $$ | |
| + | W _ {m} \rightarrow O \setminus \mathfrak p \rightarrow ( O/ \mathfrak p ) ^ \times = F ^ \times , | ||
| + | $$ | ||
| − | + | so that $ m $ | |
| + | divides $ q - 1 $ | ||
| + | with $ q = N ( \mathfrak p ) = | F | $. | ||
| + | This induces a bijection $ f : {W _ {m} } \rightarrow {( F ^ \times ) ^ {( q - 1 ) /m } } $. | ||
| + | Define a character $ {\chi _ {\mathfrak p} } : {F ^ \times } \rightarrow {W _ {m} } $ | ||
| + | of order $ m $ | ||
| + | by | ||
| − | + | $$ | |
| + | \chi _ {\mathfrak p} ( x ) = f ^ {- 1 } ( x ^ {( q - 1 ) /m } ) | ||
| + | $$ | ||
| − | for | + | for $ x \in F ^ \times $. |
| + | One can now make up the [[Gauss sum|Gauss sum]] | ||
| − | + | $$ | |
| + | g _ {a} ( \mathfrak p ) = - \sum _ {x \in F ^ \times } \chi _ {\mathfrak p} ( x ) ^ {a} \cdot \psi _ {\mathfrak p} ( x ) | ||
| + | $$ | ||
| − | + | for $ a \in \mathbf Z $. | |
| + | For a real number $ x $, | ||
| + | let $ \langle x \rangle $ | ||
| + | be the number uniquely determined by $ x \equiv \langle x \rangle ( { \mathop{\rm mod} } \mathbf Z ) $ | ||
| + | and $ 0 \leq \langle x \rangle < 1 $. | ||
| + | For $ t ( { \mathop{\rm mod} } m ) $ | ||
| + | with $ { \mathop{\rm gcd} } ( t,m ) = 1 $, | ||
| + | let $ \sigma _ {t} $ | ||
| + | be the element of $ G $ | ||
| + | corresponding to $ t ( { \mathop{\rm mod} } m ) $ | ||
| + | by $ G \simeq ( \mathbf Z/m \mathbf Z ) ^ \times $. | ||
| + | For $ a \in \mathbf Z $, | ||
| + | let $ \theta ( a ) \in \mathbf Q [ G ] $ | ||
| + | be the element | ||
| − | + | $$ | |
| + | \theta ( a ) = \sum _ {t ( { \mathop{\rm mod} } m ) } \left \langle {- { | ||
| + | \frac{at }{m} | ||
| + | } } \right \rangle \sigma _ {t} ^ {- 1 } . | ||
| + | $$ | ||
| − | For a | + | L. Stickelberger proved the following theorem: For $ r \geq 1 $, |
| + | $ a _ {1} \dots a _ {r} ,b _ {1} \dots b _ {r} \in \mathbf Z $ | ||
| + | one has $ \sum _ {i = 1 } ^ {r} a _ {i} \theta ( b _ {i} ) \in \mathbf Z [ G ] $ | ||
| + | if and only if $ \sum a _ {i} b _ {i} \equiv 0 ( { \mathop{\rm mod} } m ) $. | ||
| + | In this case, for any prime ideal $ \mathfrak p $ | ||
| + | prime to $ m $ | ||
| + | one has $ \prod _ {i = 1 } ^ {m} g _ {b _ {i} } ( \mathfrak p ) ^ {a _ {i} } \in K _ {m} $ | ||
| + | and $ \mathfrak p ^ {\sum _ {i = 1 } ^ {r} a _ {i} \theta ( b _ {i} ) } $ | ||
| + | is the principal ideal generated by $ \prod _ {i = 1 } ^ {m} g _ {b _ {i} } ( \mathfrak p ) ^ {a _ {i} } $. | ||
| − | + | The ideal $ S = \{ {\sum _ {i = 1 } ^ {r} a _ {i} \theta ( b _ {i} ) } : {\sum a _ {i} b _ {i} \equiv 0 ( { \mathop{\rm mod} } m ) } \} $ | |
| + | in $ \mathbf Z [ G ] $ | ||
| + | is called the Stickelberger ideal for $ K _ {m} $, | ||
| + | and an element of $ S $ | ||
| + | is called a Stickelberger operator for $ K _ {m} $. | ||
| + | Since any class of $ C $ | ||
| + | contains a prime ideal $ \mathfrak p $ | ||
| + | prime to $ m $, | ||
| + | Stickelberger's theorem implies that $ S $ | ||
| + | annihilates $ C $: | ||
| + | $ S \cdot C = 0 $. | ||
| − | 1) | + | For a $ \mathbf Z [ G ] $- |
| + | module $ A $, | ||
| + | one defines $ A ^ {-} = \{ {a \in A } : {( 1 + J ) a = 0 } \} $, | ||
| + | where $ J = \sigma _ {- 1 } $ | ||
| + | corresponds to complex conjugation. | ||
| − | + | Let $ g $ | |
| + | be the number of primes that ramify in $ K _ {m} $. | ||
| + | Now, | ||
| − | These results have, to some extent, been generalized to absolute Abelian fields. Stickelberger ideals are also used to construct a | + | 1) if $ g = 1 $, |
| + | then $ [ \mathbf Z [ G ] ^ {-} :S ^ {-} ] = h ^ {-} $, | ||
| + | where $ h ^ {-} $ | ||
| + | is the relative class number of $ K _ {m} $( | ||
| + | Iwasawa's theorem); | ||
| + | |||
| + | 2) if $ g \geq 2 $, | ||
| + | then $ [ \mathbf Z [ G ] ^ {-} :S ^ {-} ] = 2 ^ {a} \cdot h ^ {-} $, | ||
| + | where $ a = 2 ^ {g - 2 } - 1 $( | ||
| + | Sinnott's theorem). | ||
| + | |||
| + | These results have, to some extent, been generalized to absolute Abelian fields. Stickelberger ideals are also used to construct a $ p $- | ||
| + | adic $ L $- | ||
| + | function [[#References|[a3]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L. Stickelberger, "Über eine Verallgemeinerung der Kreistheilung" ''Math. Ann.'' , '''37''' (1890) pp. 321–367</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> K. Iwasawa, "A class number formula for cyclotomic fields" ''Ann. of Math. (2)'' , '''76''' (1962) pp. 171–179</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> K. Iwasawa, "Lectures on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110280/s11028093.png" />-adic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110280/s11028094.png" />-functions" , ''Ann. Math. Studies'' , '''74''' , Princeton Univ. Press (1972)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> W. Sinnott, "On the Stickelberger ideal and the circular units of a cyclotomic field" ''Ann. of Math. (2)'' , '''108''' (1978) pp. 107–134</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> W. Sinnott, "On the Stickelberger ideal and the circular units of an abelian field" ''Invent. Math.'' , '''62''' (1980/1) pp. 181–234</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> T. Kimura, K. Horie, "On the Stickelberger ideal and the relative class number" ''Trans. Amer. Math. Soc.'' , '''302''' (1987) pp. 727–739</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> S. Lang, "Cyclotomic fields" , '''1–2''' , Springer (1990)</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> L.C. Washington, "Introduction to cyclotomic fields" , Springer (1982)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L. Stickelberger, "Über eine Verallgemeinerung der Kreistheilung" ''Math. Ann.'' , '''37''' (1890) pp. 321–367</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> K. Iwasawa, "A class number formula for cyclotomic fields" ''Ann. of Math. (2)'' , '''76''' (1962) pp. 171–179</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> K. Iwasawa, "Lectures on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110280/s11028093.png" />-adic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110280/s11028094.png" />-functions" , ''Ann. Math. Studies'' , '''74''' , Princeton Univ. Press (1972)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> W. Sinnott, "On the Stickelberger ideal and the circular units of a cyclotomic field" ''Ann. of Math. (2)'' , '''108''' (1978) pp. 107–134</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> W. Sinnott, "On the Stickelberger ideal and the circular units of an abelian field" ''Invent. Math.'' , '''62''' (1980/1) pp. 181–234</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> T. Kimura, K. Horie, "On the Stickelberger ideal and the relative class number" ''Trans. Amer. Math. Soc.'' , '''302''' (1987) pp. 727–739</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> S. Lang, "Cyclotomic fields" , '''1–2''' , Springer (1990)</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> L.C. Washington, "Introduction to cyclotomic fields" , Springer (1982)</TD></TR></table> | ||
Revision as of 08:23, 6 June 2020
Let $ m $
be a fixed natural number and $ K _ {m} $
the cyclotomic field generated by a primitive $ m $
th root of unity over the rational number field $ \mathbf Q $.
Let $ G \simeq ( \mathbf Z/m \mathbf Z ) ^ \times $
be its Galois group and $ \mathbf Z [ G ] $
the group ring of $ G $(
cf. also Group algebra; Cross product) over the rational integers $ \mathbf Z $.
They act on ideals and on the ideal class group $ C $
of $ K _ {m} $(
cf. Class field theory). The Stickelberger ideal $ S $
is an ideal in $ \mathbf Z [ G ] $
annihilating $ C $
and related with the relative class number $ h ^ {-} $
of $ K _ {m} $.
It is defined as follows.
Let $ O $ be the ring of integers of $ K _ {m} $ and $ \mathfrak p $ a prime ideal of $ O $ that is prime to $ m $. Let $ p $ be a prime integer satisfying $ ( p ) = \mathfrak p \cap \mathbf Z $ and let $ \mathbf F _ {p} = \mathbf Z/p \mathbf Z $ be the prime field. Define a mapping $ {\psi _ {0} } : {\mathbf F _ {p} } \rightarrow {\mathbf C ^ \times = \mathbf C \setminus \{ 0 \} } $ by
$$ \psi _ {0} ( a ) = { \mathop{\rm exp} } \left ( { \frac{2 \pi i }{p} } a \right ) , $$
where $ \mathbf C $ is the complex number field. Let $ F = O/ \mathfrak p $ be the residue field and define $ {\psi _ {\mathfrak p} } : F \rightarrow {\mathbf C ^ \times } $ by composition of $ \psi _ {0} $ and the trace mapping $ T : F \rightarrow {\mathbf F _ {p} } $, i.e., $ \psi _ {\mathfrak p} = \psi _ {0} \circ T $. Let $ W _ {m} $ be the group of unities in $ K _ {m} $. Then there is an injection
$$ W _ {m} \rightarrow O \setminus \mathfrak p \rightarrow ( O/ \mathfrak p ) ^ \times = F ^ \times , $$
so that $ m $ divides $ q - 1 $ with $ q = N ( \mathfrak p ) = | F | $. This induces a bijection $ f : {W _ {m} } \rightarrow {( F ^ \times ) ^ {( q - 1 ) /m } } $. Define a character $ {\chi _ {\mathfrak p} } : {F ^ \times } \rightarrow {W _ {m} } $ of order $ m $ by
$$ \chi _ {\mathfrak p} ( x ) = f ^ {- 1 } ( x ^ {( q - 1 ) /m } ) $$
for $ x \in F ^ \times $. One can now make up the Gauss sum
$$ g _ {a} ( \mathfrak p ) = - \sum _ {x \in F ^ \times } \chi _ {\mathfrak p} ( x ) ^ {a} \cdot \psi _ {\mathfrak p} ( x ) $$
for $ a \in \mathbf Z $. For a real number $ x $, let $ \langle x \rangle $ be the number uniquely determined by $ x \equiv \langle x \rangle ( { \mathop{\rm mod} } \mathbf Z ) $ and $ 0 \leq \langle x \rangle < 1 $. For $ t ( { \mathop{\rm mod} } m ) $ with $ { \mathop{\rm gcd} } ( t,m ) = 1 $, let $ \sigma _ {t} $ be the element of $ G $ corresponding to $ t ( { \mathop{\rm mod} } m ) $ by $ G \simeq ( \mathbf Z/m \mathbf Z ) ^ \times $. For $ a \in \mathbf Z $, let $ \theta ( a ) \in \mathbf Q [ G ] $ be the element
$$ \theta ( a ) = \sum _ {t ( { \mathop{\rm mod} } m ) } \left \langle {- { \frac{at }{m} } } \right \rangle \sigma _ {t} ^ {- 1 } . $$
L. Stickelberger proved the following theorem: For $ r \geq 1 $, $ a _ {1} \dots a _ {r} ,b _ {1} \dots b _ {r} \in \mathbf Z $ one has $ \sum _ {i = 1 } ^ {r} a _ {i} \theta ( b _ {i} ) \in \mathbf Z [ G ] $ if and only if $ \sum a _ {i} b _ {i} \equiv 0 ( { \mathop{\rm mod} } m ) $. In this case, for any prime ideal $ \mathfrak p $ prime to $ m $ one has $ \prod _ {i = 1 } ^ {m} g _ {b _ {i} } ( \mathfrak p ) ^ {a _ {i} } \in K _ {m} $ and $ \mathfrak p ^ {\sum _ {i = 1 } ^ {r} a _ {i} \theta ( b _ {i} ) } $ is the principal ideal generated by $ \prod _ {i = 1 } ^ {m} g _ {b _ {i} } ( \mathfrak p ) ^ {a _ {i} } $.
The ideal $ S = \{ {\sum _ {i = 1 } ^ {r} a _ {i} \theta ( b _ {i} ) } : {\sum a _ {i} b _ {i} \equiv 0 ( { \mathop{\rm mod} } m ) } \} $ in $ \mathbf Z [ G ] $ is called the Stickelberger ideal for $ K _ {m} $, and an element of $ S $ is called a Stickelberger operator for $ K _ {m} $. Since any class of $ C $ contains a prime ideal $ \mathfrak p $ prime to $ m $, Stickelberger's theorem implies that $ S $ annihilates $ C $: $ S \cdot C = 0 $.
For a $ \mathbf Z [ G ] $- module $ A $, one defines $ A ^ {-} = \{ {a \in A } : {( 1 + J ) a = 0 } \} $, where $ J = \sigma _ {- 1 } $ corresponds to complex conjugation.
Let $ g $ be the number of primes that ramify in $ K _ {m} $. Now,
1) if $ g = 1 $, then $ [ \mathbf Z [ G ] ^ {-} :S ^ {-} ] = h ^ {-} $, where $ h ^ {-} $ is the relative class number of $ K _ {m} $( Iwasawa's theorem);
2) if $ g \geq 2 $, then $ [ \mathbf Z [ G ] ^ {-} :S ^ {-} ] = 2 ^ {a} \cdot h ^ {-} $, where $ a = 2 ^ {g - 2 } - 1 $( Sinnott's theorem).
These results have, to some extent, been generalized to absolute Abelian fields. Stickelberger ideals are also used to construct a $ p $- adic $ L $- function [a3].
References
| [a1] | L. Stickelberger, "Über eine Verallgemeinerung der Kreistheilung" Math. Ann. , 37 (1890) pp. 321–367 |
| [a2] | K. Iwasawa, "A class number formula for cyclotomic fields" Ann. of Math. (2) , 76 (1962) pp. 171–179 |
| [a3] | K. Iwasawa, "Lectures on 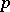 -adic -adic 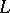 -functions" , Ann. Math. Studies , 74 , Princeton Univ. Press (1972) -functions" , Ann. Math. Studies , 74 , Princeton Univ. Press (1972) |
| [a4] | W. Sinnott, "On the Stickelberger ideal and the circular units of a cyclotomic field" Ann. of Math. (2) , 108 (1978) pp. 107–134 |
| [a5] | W. Sinnott, "On the Stickelberger ideal and the circular units of an abelian field" Invent. Math. , 62 (1980/1) pp. 181–234 |
| [a6] | T. Kimura, K. Horie, "On the Stickelberger ideal and the relative class number" Trans. Amer. Math. Soc. , 302 (1987) pp. 727–739 |
| [a7] | S. Lang, "Cyclotomic fields" , 1–2 , Springer (1990) |
| [a8] | L.C. Washington, "Introduction to cyclotomic fields" , Springer (1982) |
Stickelberger ideal. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stickelberger_ideal&oldid=48836