Stickelberger ideal
Let 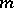 be a fixed natural number and
be a fixed natural number and 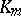 the cyclotomic field generated by a primitive
the cyclotomic field generated by a primitive 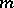 th root of unity over the rational number field
th root of unity over the rational number field 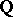 . Let
. Let 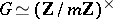 be its Galois group and
be its Galois group and  the group ring of
the group ring of  (cf. also Group algebra; Cross product) over the rational integers
(cf. also Group algebra; Cross product) over the rational integers 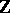 . They act on ideals and on the ideal class group
. They act on ideals and on the ideal class group 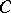 of
of 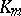 (cf. Class field theory). The Stickelberger ideal
(cf. Class field theory). The Stickelberger ideal 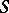 is an ideal in
is an ideal in 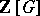 annihilating
annihilating 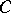 and related with the relative class number
and related with the relative class number 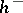 of
of 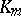 . It is defined as follows.
. It is defined as follows.
Let 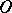 be the ring of integers of
be the ring of integers of 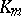 and
and 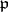 a prime ideal of
a prime ideal of 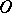 that is prime to
that is prime to 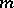 . Let
. Let  be a prime integer satisfying
be a prime integer satisfying 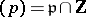 and let
and let 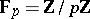 be the prime field. Define a mapping
be the prime field. Define a mapping 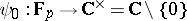 by
by
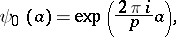 |
where 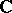 is the complex number field. Let
is the complex number field. Let  be the residue field and define
be the residue field and define  by composition of
by composition of 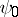 and the trace mapping
and the trace mapping  , i.e.,
, i.e., 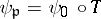 . Let
. Let  be the group of unities in
be the group of unities in 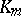 . Then there is an injection
. Then there is an injection
 |
so that 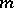 divides
divides 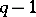 with
with  . This induces a bijection
. This induces a bijection 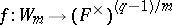 . Define a character
. Define a character 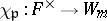 of order
of order 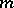 by
by
 |
for  . One can now make up the Gauss sum
. One can now make up the Gauss sum
 |
for  . For a real number
. For a real number  , let
, let  be the number uniquely determined by
be the number uniquely determined by 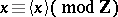 and
and 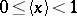 . For
. For  with
with 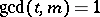 , let
, let  be the element of
be the element of  corresponding to
corresponding to 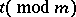 by
by 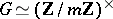 . For
. For  , let
, let 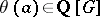 be the element
be the element
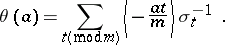 |
L. Stickelberger proved the following theorem: For 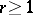 ,
, 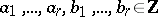 one has
one has 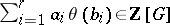 if and only if
if and only if  . In this case, for any prime ideal
. In this case, for any prime ideal 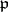 prime to
prime to 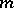 one has
one has 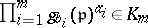 and
and  is the principal ideal generated by
is the principal ideal generated by 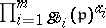 .
.
The ideal 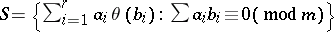 in
in 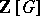 is called the Stickelberger ideal for
is called the Stickelberger ideal for 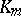 , and an element of
, and an element of 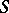 is called a Stickelberger operator for
is called a Stickelberger operator for 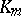 . Since any class of
. Since any class of 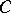 contains a prime ideal
contains a prime ideal 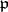 prime to
prime to  , Stickelberger's theorem implies that
, Stickelberger's theorem implies that 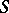 annihilates
annihilates 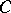 :
: 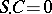 .
.
For a 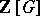 -module
-module  , one defines
, one defines  , where
, where  corresponds to complex conjugation.
corresponds to complex conjugation.
Let 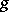 be the number of primes that ramify in
be the number of primes that ramify in 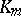 . Now,
. Now,
1) if 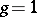 , then
, then 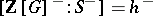 , where
, where 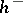 is the relative class number of
is the relative class number of 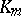 (Iwasawa's theorem);
(Iwasawa's theorem);
2) if 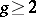 , then
, then 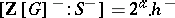 , where
, where  (Sinnott's theorem).
(Sinnott's theorem).
These results have, to some extent, been generalized to absolute Abelian fields. Stickelberger ideals are also used to construct a 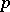 -adic
-adic 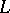 -function [a3].
-function [a3].
References
| [a1] | L. Stickelberger, "Über eine Verallgemeinerung der Kreistheilung" Math. Ann. , 37 (1890) pp. 321–367 |
| [a2] | K. Iwasawa, "A class number formula for cyclotomic fields" Ann. of Math. (2) , 76 (1962) pp. 171–179 |
| [a3] | K. Iwasawa, "Lectures on 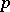 -adic -adic 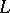 -functions" , Ann. Math. Studies , 74 , Princeton Univ. Press (1972) -functions" , Ann. Math. Studies , 74 , Princeton Univ. Press (1972) |
| [a4] | W. Sinnott, "On the Stickelberger ideal and the circular units of a cyclotomic field" Ann. of Math. (2) , 108 (1978) pp. 107–134 |
| [a5] | W. Sinnott, "On the Stickelberger ideal and the circular units of an abelian field" Invent. Math. , 62 (1980/1) pp. 181–234 |
| [a6] | T. Kimura, K. Horie, "On the Stickelberger ideal and the relative class number" Trans. Amer. Math. Soc. , 302 (1987) pp. 727–739 |
| [a7] | S. Lang, "Cyclotomic fields" , 1–2 , Springer (1990) |
| [a8] | L.C. Washington, "Introduction to cyclotomic fields" , Springer (1982) |
Stickelberger ideal. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stickelberger_ideal&oldid=18373