Difference between revisions of "Spectral theory of differential operators"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | s0865301.png | ||
| + | $#A+1 = 270 n = 2 | ||
| + | $#C+1 = 270 : ~/encyclopedia/old_files/data/S086/S.0806530 Spectral theory of differential operators | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
The branch of the general [[Spectral theory|spectral theory]] of operators in which one investigates the spectral properties of differential operators on various function spaces, especially on Hilbert spaces of measurable functions. | The branch of the general [[Spectral theory|spectral theory]] of operators in which one investigates the spectral properties of differential operators on various function spaces, especially on Hilbert spaces of measurable functions. | ||
| − | Let | + | Let $ \Omega _ {n} $ |
| + | be a domain in $ \mathbf R ^ {n} $, | ||
| + | let $ \Gamma $ | ||
| + | be its boundary, let | ||
| − | + | $$ \tag{1 } | |
| + | l ( x , D ) = \sum _ {| \alpha | \leq m } | ||
| + | a _ \alpha ( x) D ^ \alpha | ||
| + | $$ | ||
be a linear differential operator, and let | be a linear differential operator, and let | ||
| − | + | $$ \tag{2 } | |
| + | l _ {j} ( u) = \sum _ {| \alpha | \leq m _ {1} } | ||
| + | b _ {\alpha , j } ( x) D ^ \alpha u \mid _ \Gamma = 0 ,\ \ | ||
| + | 1 \leq j \leq N , | ||
| + | $$ | ||
| − | be the boundary conditions, defined by linear differential operators | + | be the boundary conditions, defined by linear differential operators $ l _ {j} $. |
Here | Here | ||
| − | + | $$ | |
| + | x = ( x _ {1} \dots x _ {n} ) ,\ \ | ||
| + | D = ( D _ {1} \dots D _ {n} ) ,\ \ | ||
| + | D _ {j} = | ||
| + | \frac \partial {\partial x _ {j} } | ||
| + | , | ||
| + | $$ | ||
| − | + | $$ | |
| + | \alpha = ( \alpha _ {1} \dots \alpha _ {n} ) , | ||
| + | $$ | ||
| − | the | + | the $ \alpha _ {j} $ |
| + | are non-negative integers, $ | \alpha | = \alpha _ {1} + \dots + \alpha _ {n} $, | ||
| + | $ D ^ \alpha = D _ {1} ^ {\alpha _ {1} } \dots D _ {n} ^ {\alpha _ {n} } $, | ||
| + | and $ a _ \alpha $ | ||
| + | and $ b _ {\alpha , j } $ | ||
| + | are functions defined in $ \Omega _ {n} $ | ||
| + | and on $ \Gamma $, | ||
| + | respectively. Unless otherwise stated, in the sequel it is assumed that $ a _ \alpha $ | ||
| + | and $ b _ {\alpha , j } $ | ||
| + | are sufficiently smooth functions when $ n > 1 $, | ||
| + | and that $ a _ {m} ( x) \neq 0 $ | ||
| + | for all $ x \in ( a , b ) $, | ||
| + | where $ \Omega _ {1} = ( a , b ) $ | ||
| + | if $ n = 1 $. | ||
==Self-adjoint extensions of differential operators.== | ==Self-adjoint extensions of differential operators.== | ||
| − | Let | + | Let $ L _ {0} ^ \prime $ |
| + | be the differential operator given by (1) on functions in $ C _ {0} ^ \infty ( \Omega _ {n} ) $, | ||
| + | that is, functions having derivatives of arbitrary order and vanishing outside a compact set lying inside $ \Omega _ {n} $. | ||
| + | If | ||
| − | + | $$ \tag{3 } | |
| + | \int\limits _ {\Omega _ {n} } l ( x, D) u \overline{v}\; dx = \ | ||
| + | \int\limits _ {\Omega _ {n} } u \overline{ {l ( x, D) v }}\; dx | ||
| + | $$ | ||
| − | for any pair of functions | + | for any pair of functions $ u $ |
| + | and $ v $ | ||
| + | in $ C _ {0} ^ \infty ( \Omega _ {n} ) $, | ||
| + | then $ L _ {0} ^ \prime $ | ||
| + | is called a symmetric differential operator, and $ l $ | ||
| + | a formally self-adjoint differential operator (cf. also [[Self-adjoint differential equation|Self-adjoint differential equation]]; [[Self-adjoint operator|Self-adjoint operator]]). Let $ L _ {0} $ | ||
| + | be the closure of $ L _ {0} ^ \prime $ | ||
| + | in $ L _ {2} ( \Omega _ {n} ) $( | ||
| + | cf. [[Closed operator|Closed operator]]). Then $ L _ {0} $ | ||
| + | and its adjoint $ L _ {0} ^ {*} $( | ||
| + | cf. [[Adjoint operator|Adjoint operator]]) are called the minimal and maximal operators, respectively, generated by $ l ( x , D ) $; | ||
| + | $ L _ {0} ^ {*} $ | ||
| + | is an extension of $ L _ {0} $. | ||
| + | An important problem in the theory of differential operators is to describe $ L _ {0} $ | ||
| + | and $ L _ {0} ^ {*} $, | ||
| + | and also to describe all self-adjoint extensions of $ L _ {0} $( | ||
| + | cf. [[Self-adjoint operator|Self-adjoint operator]]). | ||
Here one can apply the abstract theory of extensions of symmetric operators (cf. [[Extension of an operator|Extension of an operator]]). However, for differential operators, self-adjoint extensions can often be successfully described in terms of boundary conditions. | Here one can apply the abstract theory of extensions of symmetric operators (cf. [[Extension of an operator|Extension of an operator]]). However, for differential operators, self-adjoint extensions can often be successfully described in terms of boundary conditions. | ||
| Line 30: | Line 95: | ||
Let | Let | ||
| − | + | $$ \tag{4 } | |
| + | H _ \pm = \{ {u ( x) } : { | ||
| + | u ( x) \in D ( L _ {0} ^ {*} ) ,\ | ||
| + | L _ {0} ^ {*} u = \pm i u } \} | ||
| + | $$ | ||
| − | be the deficiency subspaces (cf. [[Deficiency subspace|Deficiency subspace]]) of the operator | + | be the deficiency subspaces (cf. [[Deficiency subspace|Deficiency subspace]]) of the operator $ L _ {0} $. |
| + | If $ \mathop{\rm dim} H _ \pm = 0 $, | ||
| + | then $ L _ {0} = L _ {0} ^ {*} $, | ||
| + | and $ L _ {0} ^ \prime $ | ||
| + | is said to be essentially self-adjoint. Any of the following conditions are sufficient for $ L _ {0} ^ \prime $ | ||
| + | to be essentially self-adjoint on $ L _ {2} ( \mathbf R ^ {n} ) $: | ||
| + | The formally self-adjoint differential operator $ l ( x , D ) $ | ||
| + | has the form | ||
| − | + | $$ \tag{5 } | |
| + | - \sum _ {k , j = 1 } ^ { n } | ||
| + | D _ {k} a _ {kj} ( x) D _ {j} + | ||
| + | q ( x) ,\ x \in \mathbf R ^ {n} , | ||
| + | $$ | ||
| − | with real coefficients, and | + | with real coefficients, and $ L _ {0} ^ \prime $ |
| + | is bounded from below; it has the form (5), is elliptic, the $ a _ {kj} $ | ||
| + | are constants, and $ q ( x) \geq - Q ( | x | ) $, | ||
| + | where $ Q ( r) $ | ||
| + | does not decrease monotonically, while the integral | ||
| − | + | $$ | |
| + | \int\limits ^ \infty Q ^ {-} 1/2 ( r) d r = \infty ; | ||
| + | $$ | ||
it has constant real coefficients; it has bounded coefficients and the principal part is of elliptic type with real constant coefficients (cf. [[Principal part of a differential operator|Principal part of a differential operator]]). | it has constant real coefficients; it has bounded coefficients and the principal part is of elliptic type with real constant coefficients (cf. [[Principal part of a differential operator|Principal part of a differential operator]]). | ||
| − | Let | + | Let $ L _ {0} $ |
| + | have finite deficiency indices $ n _ \pm = \mathop{\rm dim} H _ \pm $, | ||
| + | which is typical for ordinary differential operators. In this case the numbers $ n _ \pm $ | ||
| + | coincide with the dimensions of the subspaces of solutions of the equations $ l ( u) = \pm i u $ | ||
| + | in $ L _ {2} ( a , b ) $. | ||
| + | Therefore $ n _ \pm < m $, | ||
| + | and the calculation of the deficiency indices of a differential operator is connected with the qualitative theory and asymptotic methods of ordinary differential equations. | ||
| − | Let | + | Let $ n = 1 $ |
| + | and $ x \in ( a , b ) $. | ||
| + | If $ n _ {+} \neq n _ {-} $, | ||
| + | then $ L _ {0} ^ \prime $ | ||
| + | does not even have one self-adjoint extension. If $ n _ {+} = n _ {-} = k $, | ||
| + | then for the self-adjointness of extensions of $ L _ {0} ^ \prime $ | ||
| + | it is necessary to give $ k $ | ||
| + | boundary conditions, and these have been completely described. Boundary value problems take a simple form when the expression $ L _ {0} ^ \prime $ | ||
| + | has two regular end-points, or has one regular end-point but $ m = 2 k $ | ||
| + | and $ n _ \pm = k $. | ||
| + | An end-point $ a $ | ||
| + | is called regular if $ a > - \infty $ | ||
| + | and $ 1 / a _ {m} ( x) $, | ||
| + | $ a _ {j} ( x) $, | ||
| + | $ 0 \leq j \leq m - 1 $, | ||
| + | are summable on $ [ a , \beta ] $ | ||
| + | for any $ \beta < b $. | ||
| − | There are examples of partial differential operators on | + | There are examples of partial differential operators on $ L _ {2} ( \mathbf R ^ {n} ) $, |
| + | $ n \geq 3 $, | ||
| + | with discontinuous coefficients and with finite deficiency indices, but their theory is still underdeveloped. Not all self-adjoint extensions of symmetric partial differential operators in a bounded domain have been described in terms of boundary conditions, but various extensions with given properties have been described. | ||
| − | Let | + | Let $ l $ |
| + | be a formally self-adjoint elliptic differential operator of even order $ m = 2 k $ | ||
| + | with real coefficients, and let $ C _ {k} ^ \infty ( \Omega _ {n} ) $ | ||
| + | be the set of all functions having derivatives of arbitrary order in the bounded closed domain $ \overline \Omega \; _ {n} $ | ||
| + | and satisfying Dirichlet-type boundary conditions $ D ^ \alpha u = 0 $, | ||
| + | $ x \in \Gamma $, | ||
| + | $ | \alpha | \leq k - 1 $. | ||
| + | Then the differential operator defined by $ l $ | ||
| + | with domain of definition $ C _ {k} ^ \infty ( \Omega _ {n} ) $ | ||
| + | is symmetric, and its closure $ L _ {m} $ | ||
| + | is self-adjoint. There are other examples of concrete self-adjoint boundary conditions for differential operators. Most complete studies have been made in the case of second-order differential operators with boundary conditions of Dirichlet-type, von Neumann-type or of the third kind. | ||
==Spectral analysis of self-adjoint differential operators.== | ==Spectral analysis of self-adjoint differential operators.== | ||
| − | Every self-adjoint differential operator | + | Every self-adjoint differential operator $ L $ |
| + | admits a spectral decomposition of the form | ||
| − | + | $$ \tag{6 } | |
| + | L = \int\limits _ {- \infty } ^ { {+ } \infty } \lambda d E _ \lambda , | ||
| + | $$ | ||
| − | where | + | where $ E _ \lambda $ |
| + | is a [[Resolution of the identity|resolution of the identity]] (into an orthogonal family of projectors). However, the general formula does not give a direct expansion with respect to the eigenfunctions of a concrete self-adjoint differential operator, and so it is important to be able to express the family $ E _ \lambda $ | ||
| + | in terms of eigenfunctions. If a self-adjoint differential operator $ L $ | ||
| + | has discrete spectrum $ \{ \lambda _ {k} \} $ | ||
| + | with corresponding orthonormalized eigenfunctions $ \{ \phi _ {k} ( x) \} $, | ||
| + | then $ E _ \lambda $ | ||
| + | is an integral operator with (spectral) kernel | ||
| − | + | $$ \tag{7 } | |
| + | E ( x , y , \lambda ) = \ | ||
| + | \sum _ {\lambda _ {k} \in ( 0 , \lambda ] } | ||
| + | \phi _ {k} ( x) \overline{ {\phi _ {k} ( y ) }}\; . | ||
| + | $$ | ||
| − | In the case of a continuous spectrum of a differential operator, the question becomes complicated: For continuous spectra there are no eigenfunctions in | + | In the case of a continuous spectrum of a differential operator, the question becomes complicated: For continuous spectra there are no eigenfunctions in $ L _ {2} ( \Omega _ {n} ) $. |
| + | However, the following results are true. | ||
| − | Let | + | Let $ L $ |
| + | be an ordinary self-adjoint differential operator of the form (1) on $ L _ {2} ( - \infty , \infty ) $, | ||
| + | and let $ \phi _ {1} ( x , \lambda ) \dots \phi _ {m} ( x , \lambda ) $ | ||
| + | be a fundamental system of solutions of the equations $ l u = \lambda u $. | ||
| + | Then there is a monotone matrix function $ \sigma ( \lambda ) = \| \sigma _ {ij} ( \lambda ) \| _ {i , j = 1 } ^ {m} $( | ||
| + | a spectral measure) such that the resolution of the identity $ E _ \lambda $ | ||
| + | of $ L $ | ||
| + | is given by the kernel | ||
| − | + | $$ \tag{8 } | |
| + | E ( x , y , \lambda ) = \int\limits _ { 0 } ^ \lambda | ||
| + | \sum _ {i , j = 1 } ^ { m } | ||
| + | \phi _ {i} ( x , \lambda ) {\phi _ {j} ( y , \lambda ) } bar d \sigma _ {ij} ( \lambda ) . | ||
| + | $$ | ||
| − | Moreover, for any function | + | Moreover, for any function $ f $ |
| + | in $ L _ {2} ( - \infty , \infty ) $ | ||
| + | the integral | ||
| − | + | $$ \tag{9 } | |
| + | \{ F _ {j} ( \lambda ) \} = \ | ||
| + | \left \{ \int\limits _ {- \infty } ^ { {+ } \infty } | ||
| + | \overline{ {\phi _ {j} ( x , \lambda ) }}\; f ( x) d x \right \} | ||
| + | $$ | ||
| − | converges in the space of vector functions | + | converges in the space of vector functions $ L _ {2} ( - \infty , \infty ; d \sigma ( \lambda ) ) $ |
| + | generated by the measure $ \sigma ( \lambda ) $, | ||
| + | and, conversely, the integral | ||
| − | + | $$ | |
| + | \int\limits _ {- \infty } ^ { {+ } \infty } \ | ||
| + | \sum _ {i , j = 1 } ^ { m } | ||
| + | F _ {i} ( \lambda ) \phi _ {j} ( x , \lambda ) d \sigma _ {ij} ( \lambda ) | ||
| + | $$ | ||
| − | converges to | + | converges to $ f ( x) $ |
| + | in $ L _ {2} ( - \infty , \infty ) $. | ||
| + | If (1) has a regular end-point $ a $ | ||
| + | and $ m = 2 k $, | ||
| + | and the deficiency indices $ n _ \pm = k $, | ||
| + | then the functions $ \phi _ {1} ( x , \lambda ) \dots \phi _ {k} ( x , \lambda ) $ | ||
| + | can be chosen to form a fundamental system in the class of solutions of the equation $ l u = \lambda u $ | ||
| + | satisfying boundary conditions at $ a $, | ||
| + | and in this case the order of the spectral measure is equal to $ k $. | ||
| − | Let | + | Let $ L $ |
| + | be a self-adjoint elliptic differential operator on $ L _ {2} ( \Omega _ {n} ) $. | ||
| + | Then its resolution of the identity $ E $ | ||
| + | is an integral operator with kernel $ E ( x , y , \lambda ) $, | ||
| + | and there is a non-decreasing function $ \rho ( \lambda ) $ | ||
| + | such that for all numbers $ \lambda _ {1} $ | ||
| + | and $ \lambda _ {2} $, | ||
| − | + | $$ \tag{10 } | |
| + | E ( x , y , \lambda _ {1} ) - | ||
| + | E ( x , y , \lambda _ {2} ) = \ | ||
| + | \int\limits _ { \lambda _ {1} } ^ { {\lambda _ 2 } } | ||
| + | \phi ( x , y , \lambda ) d \rho ( \lambda ) , | ||
| + | $$ | ||
| − | where, for every | + | where, for every $ \lambda $, |
| + | there is a finite or infinite system $ \{ \phi _ {j} ( x , \lambda ) \} $ | ||
| + | of solutions of the equation $ l u = \lambda u $ | ||
| + | and | ||
| − | + | $$ \tag{11 } | |
| + | \phi ( x , y , \lambda ) = \ | ||
| + | \sum _ { j } \phi _ {j} ( x , \lambda ) \overline{ {\phi _ {j} ( y , \lambda ) }}\; . | ||
| + | $$ | ||
| − | For the Schrödinger operator | + | For the Schrödinger operator $ L u = - \Delta u + q ( x) u $, |
| + | $ x \in \mathbf R ^ {3} $, | ||
| + | under the condition $ | q ( x) | \leq c ( 1 + | x | ) ^ {- 2 - \epsilon } $, | ||
| + | the kernel $ E ( x , y , \lambda ) $ | ||
| + | can be explicitly expressed in terms of the solutions of the [[Dispersion equation|dispersion equation]]. | ||
| − | The formulas (10), (11) also hold for arbitrary self-adjoint partial differential operators, and in this case the | + | The formulas (10), (11) also hold for arbitrary self-adjoint partial differential operators, and in this case the $ \{ \phi _ {j} ( x , \lambda ) \} $ |
| + | may be generalized functions, but they are of finite order. | ||
The nature of the convergence of the expansion into eigenfunctions and the asymptotic properties of the spectral kernel help to justify the [[Fourier method|Fourier method]] for solving the equations of mathematical physics. For ordinary differential operators, there is the following final result, the so-called equiconvergence theorem: The expansion of a given summable function into the eigenfunctions of a differential operator which is bounded from below and the Fourier integral are both convergent or both divergent (i.e. equi-convergent) at any point. For partial differential operators, the question becomes complicated. | The nature of the convergence of the expansion into eigenfunctions and the asymptotic properties of the spectral kernel help to justify the [[Fourier method|Fourier method]] for solving the equations of mathematical physics. For ordinary differential operators, there is the following final result, the so-called equiconvergence theorem: The expansion of a given summable function into the eigenfunctions of a differential operator which is bounded from below and the Fourier integral are both convergent or both divergent (i.e. equi-convergent) at any point. For partial differential operators, the question becomes complicated. | ||
| Line 92: | Line 279: | ||
This theory is concerned with the study of the nature of the spectrum in relation to the behaviour of the coefficients, the geometry of the domain and the boundary conditions. | This theory is concerned with the study of the nature of the spectrum in relation to the behaviour of the coefficients, the geometry of the domain and the boundary conditions. | ||
| − | There is a series of tests for the discreteness of the spectrum of a differential operator. The most general are the following criterion and its generalizations: If | + | There is a series of tests for the discreteness of the spectrum of a differential operator. The most general are the following criterion and its generalizations: If $ q ( x) \geq 1 $, |
| + | then the spectrum of the differential operator generated by the expression $ l u = - u ^ {\prime\prime} + q ( x ) u $ | ||
| + | on $ L _ {2} ( - \infty , \infty ) $ | ||
| + | is discrete if and only if for any $ j > 0 $, | ||
| − | + | $$ | |
| + | \lim\limits _ {| x | \rightarrow \infty } \ | ||
| + | \int\limits _ { x } ^ { {x } + j } q ( t) d t = \infty . | ||
| + | $$ | ||
| − | The generalization of this criterion to partial differential operators takes a more complicated form. There are other, simpler, tests for discreteness of the spectrum of a differential operator. For example, the self-adjoint differential operator generated by (5) has discrete spectrum if | + | The generalization of this criterion to partial differential operators takes a more complicated form. There are other, simpler, tests for discreteness of the spectrum of a differential operator. For example, the self-adjoint differential operator generated by (5) has discrete spectrum if $ q ( x) \rightarrow \infty $ |
| + | as $ | x | \rightarrow \infty $. | ||
| + | The self-adjoint differential operator $ L _ {m} $ | ||
| + | has discrete spectrum. | ||
| − | The study of the nature of a spectrum when there is a continuous part is a difficult problem. Here are some results: 1) if an ordinary differential operator is defined by a formally self-adjoint expression (1) with periodic coefficients on | + | The study of the nature of a spectrum when there is a continuous part is a difficult problem. Here are some results: 1) if an ordinary differential operator is defined by a formally self-adjoint expression (1) with periodic coefficients on $ ( - \infty , \infty ) $ |
| + | having a common period, then its spectrum is continuous and consists of a sequence of disjoint intervals whose end-points tend to $ - \infty $ | ||
| + | or $ + \infty $; | ||
| + | 2) if a differential operator is defined by the expression $ ( - 1 ) ^ {k} ( D _ {1} ^ {2} + \dots + D _ {n} ^ {2} ) ^ {k} + q ( x ) $ | ||
| + | on $ L _ {2} ( \mathbf R ^ {n} ) $ | ||
| + | and $ \lim\limits q ( x) = 0 $ | ||
| + | as $ | x | \rightarrow + \infty $, | ||
| + | then its continuous spectrum fills $ [ 0 , \infty ] $, | ||
| + | while its negative spectrum is discrete and can have a limit point at zero only. If $ k = 1 $, | ||
| + | $ | q ( x) | \leq M ( | x | ) $ | ||
| + | and | ||
| − | < | + | $$ |
| + | \int\limits ^ \infty r M ( r) d r < \infty \ \ | ||
| + | ( M ( r) = O ( r ^ {-} 1 ) ) , | ||
| + | $$ | ||
then the negative spectrum is finite (there are no eigenvalues in the continuous spectrum). | then the negative spectrum is finite (there are no eigenvalues in the continuous spectrum). | ||
| Line 107: | Line 316: | ||
==Functions of a self-adjoint differential operator.== | ==Functions of a self-adjoint differential operator.== | ||
| − | These are studied with the aim of solving mixed problems for differential equations, and also for problems in the theory of differential operators. Let | + | These are studied with the aim of solving mixed problems for differential equations, and also for problems in the theory of differential operators. Let $ l $ |
| + | be an elliptic differential operator of order $ m $. | ||
| + | The [[Resolvent|resolvent]] $ ( L + \lambda ) ^ {-} 1 $ | ||
| + | when $ \lambda > 0 $, | ||
| + | and the functions $ \mathop{\rm exp} ( - L t ) $ | ||
| + | and $ \mathop{\rm exp} ( i L ^ {1/m} t ) $ | ||
| + | when $ t > 0 $, | ||
| + | have been thoroughly studied. The latter are solution operators for the generalized heat equation $ u _ {t} = - L u $, | ||
| + | $ u ( 0 , x ) = f ( x) $, | ||
| + | and the generalized wave equation $ u _ {t} = i L ^ {1/m} u $, | ||
| + | $ u ( 0 , x ) = f ( x) $, | ||
| + | respectively. All three operator-functions are integral functions, and have kernels $ R ( x , y , \lambda ) $, | ||
| + | $ K ( x , y , \lambda ) $, | ||
| + | $ G ( x , y , t ) $( | ||
| + | Green functions), respectively. The formula | ||
| − | + | $$ \tag{12 } | |
| + | R ( x , y , \lambda ) = \int\limits _ { 0 } ^ \infty | ||
| + | e ^ {- \lambda t } K ( x , y , t ) d t | ||
| + | $$ | ||
| − | establishes a connection between | + | establishes a connection between $ R $ |
| + | and $ K $. | ||
| + | Some properties of $ R ( x , y , \lambda ) $ | ||
| + | are: If $ L $ | ||
| + | is an elliptic self-adjoint differential operator of order $ m $ | ||
| + | on $ L _ {2} ( \Omega _ {n} ) $, | ||
| + | then to $ ( L + \lambda ) ^ {-} p $ | ||
| + | there corresponds a kernel of Carleman type when $ p > n / 2 m $; | ||
| + | when $ p > n / m $, | ||
| + | $ ( L _ {m} + \lambda ) ^ {-} p $ | ||
| + | is nuclear, and therefore | ||
| − | + | $$ \tag{13 } | |
| + | S _ {p} ( L + \lambda ) ^ {-} p = \ | ||
| + | \sum _ { k= } 1 ^ \infty ( \lambda _ {k} + \lambda ) ^ {-} p , | ||
| + | $$ | ||
| − | where | + | where $ \{ \lambda _ {k} \} $ |
| + | are the eigenvalues of $ L _ {m} $. | ||
| + | There are also other tests of nuclearity for $ ( L + \lambda ) ^ {-} p $ | ||
| + | on $ L _ {2} ( \mathbf R ^ {n} ) $. | ||
| − | The analytic and asymptotic properties of Green functions give useful information about the spectral nature of a differential operator | + | The analytic and asymptotic properties of Green functions give useful information about the spectral nature of a differential operator $ L $. |
| + | For example, if in (13) the behaviour of $ S _ {p} ( L + \lambda ) ^ {-} p $ | ||
| + | as $ \lambda \rightarrow \infty $ | ||
| + | is known, then the application of Tauberian theorems enables one to find the asymptotics of $ \lambda _ {k} $. | ||
| + | The same can be done if one knows the asymptotics of $ S _ {p} \mathop{\rm exp} ( - L t ) $ | ||
| + | as $ t \rightarrow + 0 $. | ||
| + | The asymptotics of $ R ( x , y , \lambda ) $ | ||
| + | and $ K ( x , y , \lambda ) $ | ||
| + | can be established, for example, by the method of parametrics, by the method of potentials, etc. The asymptotics of $ \lambda _ {k} $ | ||
| + | have thus been found for an extensive class of elliptic differential operators. To determine the asymptotics of the spectral kernel $ E ( x , y , \lambda ) $ | ||
| + | of an elliptic differential operator, the study of the asymptotics of the kernel $ G ( x , y , t ) $ | ||
| + | as $ t \rightarrow 0 $ | ||
| + | has proved effective in conjunction with subsequent application of various Tauberian theorems. In particular, when $ x = y $, | ||
| + | $ x \notin \Gamma $, | ||
| − | + | $$ | |
| + | E ( x , x , \lambda ) = ( 2 \pi ) ^ {-} n | ||
| + | \int\limits _ {l _ {0} ( x , \xi ) < \lambda } \ | ||
| + | d \xi + O ( \lambda ^ {( n - 1 ) / m } ) . | ||
| + | $$ | ||
==Non-self-adjoint differential operators.== | ==Non-self-adjoint differential operators.== | ||
| − | Most complete results have been obtained for ordinary differential operators on a finite interval. Let | + | Most complete results have been obtained for ordinary differential operators on a finite interval. Let $ L $ |
| + | be the differential operator defined by (1) when $ n = 1 $ | ||
| + | and $ a _ {m} ( x) \equiv 1 $ | ||
| + | on functions having $ m - 1 $ | ||
| + | absolutely-continuous derivatives and satisfying the boundary conditions: | ||
| − | + | $$ | |
| + | l _ { \nu _ {0} } ( u) + l _ {\nu _ {1} } | ||
| + | ( u) \equiv \alpha _ \nu u ^ {( k _ \nu ) } | ||
| + | ( 0) + \sum _ { j= } 0 ^ { {k _ \nu } - 1 } \alpha _ {\nu _ {j} } u ^ {(} j) ( 0) + | ||
| + | $$ | ||
| − | + | $$ | |
| + | + | ||
| + | \beta _ \nu u ^ {( k _ \nu ) } ( 1) + \sum _ { j= } 0 ^ { { } | ||
| + | k _ \nu - 1 } \beta _ {\nu _ {j} } u ^ {(} j) ( 1) = 0 ,\ 1 \leq \nu \leq m . | ||
| + | $$ | ||
| − | Here | + | Here $ m - 1 \geq k _ {1} \geq \dots \geq k _ {m} \geq 0 $, |
| + | $ k _ {\nu - 2 } < k _ \nu $ | ||
| + | and $ \alpha _ \nu , \beta _ \nu $ | ||
| + | do not simultaneously vanish. Let the boundary conditions (2) be regular. This holds for boundary conditions of Sturm–Liouville type ( $ m = 2 k $, | ||
| + | $ l _ {\nu 0 } ( u) = l _ {\nu 1 } ( u) = 0 $, | ||
| + | $ 1 \leq \nu \leq m - 1 $), | ||
| + | and also for periodic-type boundary conditions $ ( \alpha _ \nu = \beta _ \nu = 1 ) $. | ||
| + | Then $ L $ | ||
| + | has an infinite number of eigenvalues, which have precise asymptotics; the system consisting of the eigenfunctions of $ L $ | ||
| + | and of their associates is complete in $ L _ {p} ( 0 , 1 ) $; | ||
| + | the expansion of functions $ f $ | ||
| + | in $ D ( L) $ | ||
| + | into eigenfunctions of $ L $ | ||
| + | and their associates converges uniformly on $ ( 0 , 1 ] $. | ||
| + | The system of eigenfunctions and their associates may also be complete under certain non-regular boundary conditions, in particular of splitting type ( $ l _ {\nu 0 } ( u) = 0 $, | ||
| + | $ 1 \leq \nu \leq m _ {1} $, | ||
| + | $ l _ {\nu 1 } ( u) = 0 $, | ||
| + | $ 1 \leq \nu = m _ {2} $, | ||
| + | $ m _ {1} \neq m _ {2} $, | ||
| + | $ m _ {1} + m _ {2} = m $). | ||
| + | However, the convergence of the expansion into a series of eigenfunctions and their associates holds only for a narrow class of ( $ l $- | ||
| + | analytic) functions. | ||
| − | Let | + | Let $ L _ {0} $ |
| + | be a self-adjoint operator on a separable Hilbert space $ H $ | ||
| + | with eigenvalues $ \{ \lambda _ {k} \} $, | ||
| + | and suppose that the operator $ L _ {0} ^ {-} p $ | ||
| + | is nuclear for a certain $ p > 0 $. | ||
| + | Let $ L _ {1} $ | ||
| + | be another operator such that $ L _ {1} L _ {0} ^ {-} 1 $ | ||
| + | is compact. Then the system consisting of the eigenvectors of $ L _ {0} + L _ {1} $ | ||
| + | and of their associates is complete in $ H $( | ||
| + | Keldysh' theorem). The application of this theorem gives classes of differential operators which have a complete system of eigenfunctions and their associates. | ||
| − | Let | + | Let $ L _ {m} $ |
| + | be a differential operator on $ L _ {2} ( \Omega _ {n} ) $ | ||
| + | and let | ||
| − | + | $$ | |
| + | L _ {1} u = \sum _ {| \alpha | \leq m - 1 } | ||
| + | d _ \alpha ( x) D ^ \alpha u . | ||
| + | $$ | ||
| − | Then the system consisting of the eigenfunctions of | + | Then the system consisting of the eigenfunctions of $ L _ {m} + L _ {1} $ |
| + | and of their associates is complete in $ L _ {2} ( \Omega _ {n} ) $. | ||
| + | However, the expansion of a function into a series with respect to this system is divergent, in general, and is conditionally summable by the generalized Abel method. | ||
| − | If | + | If $ \Omega _ {n} $ |
| + | is an unbounded domain, then to satisfy the conditions of Keldysh' theorem one must impose further conditions on the growth of the coefficient functions of the differential operator. | ||
| − | Non-self-adjoint differential operators with a continuous part in their spectrum have not been studied much. This is connected with the fact that no analogue of the spectral decomposition theorem exists in this case. An exception is the differential operator generated by the expression | + | Non-self-adjoint differential operators with a continuous part in their spectrum have not been studied much. This is connected with the fact that no analogue of the spectral decomposition theorem exists in this case. An exception is the differential operator generated by the expression $ - d ^ {2} u / d x ^ {2} + q ( x) $ |
| + | where $ x \in [ 0 , \infty ) $ | ||
| + | or $ x \in ( - \infty , \infty ) $ | ||
| + | and $ q ( x) $ | ||
| + | is a complex-valued function. Let $ \phi ( x , k ) $ | ||
| + | be the solution of the equation $ - u ^ {(} 2) + q ( x ) u = k ^ {2} u $ | ||
| + | for $ 0 \leq x < \infty $ | ||
| + | satisfying the initial conditions $ \phi ( 0 , k ) = 1 $, | ||
| + | $ \phi ^ \prime ( 0 , k ) = 0 $. | ||
| + | Let $ f _ {1} $ | ||
| + | and $ f _ {2} $ | ||
| + | be functions in $ L _ {2} ( 0 , \infty ) $ | ||
| + | of compact support and let | ||
| − | + | $$ | |
| + | F _ {j} ( k) = \int\limits _ { 0 } ^ \infty | ||
| + | f _ {j} ( x) \phi ( x , k ) d x . | ||
| + | $$ | ||
| − | Then there is a linear functional | + | Then there is a linear functional $ R $ |
| + | on a linear topological space $ G $ | ||
| + | such that $ F _ {1} F _ {2} \in G $ | ||
| + | and | ||
| − | + | $$ | |
| + | ( R , F _ {1} F _ {2} ) = \ | ||
| + | \int\limits _ { 0 } ^ \infty f _ {1} ( x) f _ {2} ( x) d x . | ||
| + | $$ | ||
| − | The space | + | The space $ G $ |
| + | is the set of all even entire functions of order of growth one and of finite type that are summable on the real axis. If $ x q ( x) \in L _ {1} ( 0 , \infty ) $, | ||
| + | then $ R $ | ||
| + | can be explicitly calculated. In this case, spectral singularities, that is, poles of the kernel of the resolvent, appear in the continuous spectrum, and these are not eigenvalues of the differential operator. Spectral singularities are inherent in non-self-adjoint operators, and because of them, questions of the expansion into eigenfunctions (and convergence problems) become more complicated. For the differential operator | ||
| − | + | $$ | |
| + | L u \equiv ( - D _ {1} ^ {2} - | ||
| + | D _ {2} ^ {2} - D _ {3} ^ {2} + q ( x) ) u | ||
| + | $$ | ||
| − | on | + | on $ L _ {2} ( \mathbf R ^ {3} ) $, |
| + | where $ q ( x) $ | ||
| + | is a complex-valued function that decreases exponentially, a form of spectral decomposition has also been found by solving a problem in dispersion theory, taking the influence of spectral singularities into account. | ||
==Inverse problems of spectral analysis.== | ==Inverse problems of spectral analysis.== | ||
| Line 161: | Line 499: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> Yu.M. [Yu.M. Berezanskii] Berezanskiy, "Expansion in eigenfunctions of selfadjoint operators" , Amer. Math. Soc. (1968) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I.M. Glazman, "Direct methods of qualitative spectral analysis of singular differential operators" , Israel Program Sci. Transl. (1965) (Translated from Russian) {{MR|0190800}} {{ZBL|0143.36505}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> N. Dunford, J.T. Schwartz, "Linear operators. Spectral theory" , '''2''' , Interscience (1963) {{MR|0188745}} {{ZBL|}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> T. Kato, "Perturbation theory for linear operators" , Springer (1976) {{MR|0407617}} {{ZBL|0342.47009}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> B.M. Levitan, I.S. Sargsyan, "Introduction to spectral theory: selfadjoint ordinary differential operators" , Amer. Math. Soc. (1975) (Translated from Russian) {{MR|0369797}} {{ZBL|0302.47036}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> V.A. Marchenko, "Sturm–Liouville operators and applications" , Birkhäuser (1986) (Translated from Russian) {{MR|0897106}} {{ZBL|0592.34011}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> M.A. Naimark, "Linear differential operators" , '''1–2''' , F. Ungar (1967–1968) (Translated from Russian) {{MR|2814127}} {{MR|0353061}} {{MR|0262880}} {{MR|0216050}} {{MR|0067292}} {{MR|0050109}} {{ZBL|1221.47085}} {{ZBL|0227.34020}} {{ZBL|0219.34001}} {{ZBL|0057.07102}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> E.C. Titchmarsh, "Eigenfunction expansions associated with second-order differential equations" , '''1''' , Clarendon Press (1962) pp. Chapts. 1; 2 {{MR|0176151}} {{ZBL|0099.05201}} </TD></TR><TR><TD valign="top">[9a]</TD> <TD valign="top"> L.D. Faddeev, "Mathematical aspects of the three-body problem in the quantum scattering theory" , Israel Program Sci. Transl. (1965) (Translated from Russian) {{MR|0221828}} {{ZBL|0131.43504}} </TD></TR><TR><TD valign="top">[9b]</TD> <TD valign="top"> L.D. Faddeev, "Properties of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086530/s086530271.png" />-matrix of the one-dimensional Schrödinger equation" ''Trudy. Mat. Inst. Steklov.'' , '''73''' (1964) pp. 314–336 (In Russian) {{MR|178188}} {{ZBL|}} </TD></TR><TR><TD valign="top">[10a]</TD> <TD valign="top"> Sh.A. Alimov, V.A. Il'in, E.M. Nikishin, "Convergence problems of multiple trigonometric series and spectral decompositions I" ''Russian Math. Surveys'' , '''31''' : 6 (1976) pp. 29–86 ''Uspekhi Mat. Nauk'' , '''31''' : 6 (1976) pp. 28–83 {{MR|}} {{ZBL|0367.42008}} </TD></TR><TR><TD valign="top">[10b]</TD> <TD valign="top"> Sh.A. Alimov, V.A. Il'in, E.M. Nikishin, "Problems of convergence of multiple trigonometric series and spectral decompositions II" ''Russian Math. Surveys'' , '''32''' : 1 (1977) pp. 115–139 ''Uspekhi Mat. Nauk'' , '''32''' : 1 (1977) pp. 107–130 {{MR|}} {{ZBL|0376.42002}} </TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> Yu.M. Berezanskii, "Self-conjugate elliptic operators with singular potential" ''Ukr. Math. J.'' , '''26''' : 5 (1974) pp. 475–483 ''Ukrain. Mat. Zh.'' , '''26''' : 5 (1974) pp. 579–590 {{MR|352725}} {{ZBL|}} </TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> M.G. Gasymov, "The inverse scattering problem for a system of Dirac equations of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086530/s086530272.png" />" ''Trans. Moscow Math. Soc.'' , '''19''' (1968) pp. 41–120 ''Trudy Moskov. Mat. Obshch.'' , '''19''' (1968) pp. 41–112 {{MR|0208944}} {{ZBL|0197.26102}} </TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> B.M. Levitan, M.G. Gasymov, "Determination of a differential equation by two of its spectra" ''Russian Math. Surveys'' , '''19''' : 2 (1964) pp. 1–63 ''Uspekhi Mat. Nauk'' , '''19''' : 2 (1964) pp. 3–63 {{MR|162996}} {{ZBL|0145.10903}} </TD></TR><TR><TD valign="top">[14]</TD> <TD valign="top"> B.A. Dubrovin, V.B. Matveev, S.P. Novikov, "Non-linear equations of Korteweg–de Vries type, finite-zone linear operators, and abelian varieties" ''Russian Math. Surveys'' , '''31''' : 1 (1976) pp. 59–146 ''Uspekhi Mat. Nauk'' , '''31''' : 1 (1976) pp. 55–136 {{MR|}} {{ZBL|0461.35074}} </TD></TR><TR><TD valign="top">[15]</TD> <TD valign="top"> A.G. Kostyuchenko, "Asymptotic behavior of the spectral function of self-adjoint elliptic operators" , ''4-th Math. Summer School'' , Kiev (1968) pp. 42–117 (In Russian)</TD></TR><TR><TD valign="top">[16]</TD> <TD valign="top"> L. Hörmander, "The spectral function of an elliptic operator" ''Acta Math.'' , '''121''' (1968) pp. 193–218 {{MR|0609014}} {{ZBL|0164.13201}} </TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> Yu.M. [Yu.M. Berezanskii] Berezanskiy, "Expansion in eigenfunctions of selfadjoint operators" , Amer. Math. Soc. (1968) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I.M. Glazman, "Direct methods of qualitative spectral analysis of singular differential operators" , Israel Program Sci. Transl. (1965) (Translated from Russian) {{MR|0190800}} {{ZBL|0143.36505}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> N. Dunford, J.T. Schwartz, "Linear operators. Spectral theory" , '''2''' , Interscience (1963) {{MR|0188745}} {{ZBL|}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> T. Kato, "Perturbation theory for linear operators" , Springer (1976) {{MR|0407617}} {{ZBL|0342.47009}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> B.M. Levitan, I.S. Sargsyan, "Introduction to spectral theory: selfadjoint ordinary differential operators" , Amer. Math. Soc. (1975) (Translated from Russian) {{MR|0369797}} {{ZBL|0302.47036}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> V.A. Marchenko, "Sturm–Liouville operators and applications" , Birkhäuser (1986) (Translated from Russian) {{MR|0897106}} {{ZBL|0592.34011}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> M.A. Naimark, "Linear differential operators" , '''1–2''' , F. Ungar (1967–1968) (Translated from Russian) {{MR|2814127}} {{MR|0353061}} {{MR|0262880}} {{MR|0216050}} {{MR|0067292}} {{MR|0050109}} {{ZBL|1221.47085}} {{ZBL|0227.34020}} {{ZBL|0219.34001}} {{ZBL|0057.07102}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> E.C. Titchmarsh, "Eigenfunction expansions associated with second-order differential equations" , '''1''' , Clarendon Press (1962) pp. Chapts. 1; 2 {{MR|0176151}} {{ZBL|0099.05201}} </TD></TR><TR><TD valign="top">[9a]</TD> <TD valign="top"> L.D. Faddeev, "Mathematical aspects of the three-body problem in the quantum scattering theory" , Israel Program Sci. Transl. (1965) (Translated from Russian) {{MR|0221828}} {{ZBL|0131.43504}} </TD></TR><TR><TD valign="top">[9b]</TD> <TD valign="top"> L.D. Faddeev, "Properties of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086530/s086530271.png" />-matrix of the one-dimensional Schrödinger equation" ''Trudy. Mat. Inst. Steklov.'' , '''73''' (1964) pp. 314–336 (In Russian) {{MR|178188}} {{ZBL|}} </TD></TR><TR><TD valign="top">[10a]</TD> <TD valign="top"> Sh.A. Alimov, V.A. Il'in, E.M. Nikishin, "Convergence problems of multiple trigonometric series and spectral decompositions I" ''Russian Math. Surveys'' , '''31''' : 6 (1976) pp. 29–86 ''Uspekhi Mat. Nauk'' , '''31''' : 6 (1976) pp. 28–83 {{MR|}} {{ZBL|0367.42008}} </TD></TR><TR><TD valign="top">[10b]</TD> <TD valign="top"> Sh.A. Alimov, V.A. Il'in, E.M. Nikishin, "Problems of convergence of multiple trigonometric series and spectral decompositions II" ''Russian Math. Surveys'' , '''32''' : 1 (1977) pp. 115–139 ''Uspekhi Mat. Nauk'' , '''32''' : 1 (1977) pp. 107–130 {{MR|}} {{ZBL|0376.42002}} </TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> Yu.M. Berezanskii, "Self-conjugate elliptic operators with singular potential" ''Ukr. Math. J.'' , '''26''' : 5 (1974) pp. 475–483 ''Ukrain. Mat. Zh.'' , '''26''' : 5 (1974) pp. 579–590 {{MR|352725}} {{ZBL|}} </TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> M.G. Gasymov, "The inverse scattering problem for a system of Dirac equations of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086530/s086530272.png" />" ''Trans. Moscow Math. Soc.'' , '''19''' (1968) pp. 41–120 ''Trudy Moskov. Mat. Obshch.'' , '''19''' (1968) pp. 41–112 {{MR|0208944}} {{ZBL|0197.26102}} </TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> B.M. Levitan, M.G. Gasymov, "Determination of a differential equation by two of its spectra" ''Russian Math. Surveys'' , '''19''' : 2 (1964) pp. 1–63 ''Uspekhi Mat. Nauk'' , '''19''' : 2 (1964) pp. 3–63 {{MR|162996}} {{ZBL|0145.10903}} </TD></TR><TR><TD valign="top">[14]</TD> <TD valign="top"> B.A. Dubrovin, V.B. Matveev, S.P. Novikov, "Non-linear equations of Korteweg–de Vries type, finite-zone linear operators, and abelian varieties" ''Russian Math. Surveys'' , '''31''' : 1 (1976) pp. 59–146 ''Uspekhi Mat. Nauk'' , '''31''' : 1 (1976) pp. 55–136 {{MR|}} {{ZBL|0461.35074}} </TD></TR><TR><TD valign="top">[15]</TD> <TD valign="top"> A.G. Kostyuchenko, "Asymptotic behavior of the spectral function of self-adjoint elliptic operators" , ''4-th Math. Summer School'' , Kiev (1968) pp. 42–117 (In Russian)</TD></TR><TR><TD valign="top">[16]</TD> <TD valign="top"> L. Hörmander, "The spectral function of an elliptic operator" ''Acta Math.'' , '''121''' (1968) pp. 193–218 {{MR|0609014}} {{ZBL|0164.13201}} </TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
Latest revision as of 08:22, 6 June 2020
The branch of the general spectral theory of operators in which one investigates the spectral properties of differential operators on various function spaces, especially on Hilbert spaces of measurable functions.
Let $ \Omega _ {n} $ be a domain in $ \mathbf R ^ {n} $, let $ \Gamma $ be its boundary, let
$$ \tag{1 } l ( x , D ) = \sum _ {| \alpha | \leq m } a _ \alpha ( x) D ^ \alpha $$
be a linear differential operator, and let
$$ \tag{2 } l _ {j} ( u) = \sum _ {| \alpha | \leq m _ {1} } b _ {\alpha , j } ( x) D ^ \alpha u \mid _ \Gamma = 0 ,\ \ 1 \leq j \leq N , $$
be the boundary conditions, defined by linear differential operators $ l _ {j} $.
Here
$$ x = ( x _ {1} \dots x _ {n} ) ,\ \ D = ( D _ {1} \dots D _ {n} ) ,\ \ D _ {j} = \frac \partial {\partial x _ {j} } , $$
$$ \alpha = ( \alpha _ {1} \dots \alpha _ {n} ) , $$
the $ \alpha _ {j} $ are non-negative integers, $ | \alpha | = \alpha _ {1} + \dots + \alpha _ {n} $, $ D ^ \alpha = D _ {1} ^ {\alpha _ {1} } \dots D _ {n} ^ {\alpha _ {n} } $, and $ a _ \alpha $ and $ b _ {\alpha , j } $ are functions defined in $ \Omega _ {n} $ and on $ \Gamma $, respectively. Unless otherwise stated, in the sequel it is assumed that $ a _ \alpha $ and $ b _ {\alpha , j } $ are sufficiently smooth functions when $ n > 1 $, and that $ a _ {m} ( x) \neq 0 $ for all $ x \in ( a , b ) $, where $ \Omega _ {1} = ( a , b ) $ if $ n = 1 $.
Self-adjoint extensions of differential operators.
Let $ L _ {0} ^ \prime $ be the differential operator given by (1) on functions in $ C _ {0} ^ \infty ( \Omega _ {n} ) $, that is, functions having derivatives of arbitrary order and vanishing outside a compact set lying inside $ \Omega _ {n} $. If
$$ \tag{3 } \int\limits _ {\Omega _ {n} } l ( x, D) u \overline{v}\; dx = \ \int\limits _ {\Omega _ {n} } u \overline{ {l ( x, D) v }}\; dx $$
for any pair of functions $ u $ and $ v $ in $ C _ {0} ^ \infty ( \Omega _ {n} ) $, then $ L _ {0} ^ \prime $ is called a symmetric differential operator, and $ l $ a formally self-adjoint differential operator (cf. also Self-adjoint differential equation; Self-adjoint operator). Let $ L _ {0} $ be the closure of $ L _ {0} ^ \prime $ in $ L _ {2} ( \Omega _ {n} ) $( cf. Closed operator). Then $ L _ {0} $ and its adjoint $ L _ {0} ^ {*} $( cf. Adjoint operator) are called the minimal and maximal operators, respectively, generated by $ l ( x , D ) $; $ L _ {0} ^ {*} $ is an extension of $ L _ {0} $. An important problem in the theory of differential operators is to describe $ L _ {0} $ and $ L _ {0} ^ {*} $, and also to describe all self-adjoint extensions of $ L _ {0} $( cf. Self-adjoint operator).
Here one can apply the abstract theory of extensions of symmetric operators (cf. Extension of an operator). However, for differential operators, self-adjoint extensions can often be successfully described in terms of boundary conditions.
Let
$$ \tag{4 } H _ \pm = \{ {u ( x) } : { u ( x) \in D ( L _ {0} ^ {*} ) ,\ L _ {0} ^ {*} u = \pm i u } \} $$
be the deficiency subspaces (cf. Deficiency subspace) of the operator $ L _ {0} $. If $ \mathop{\rm dim} H _ \pm = 0 $, then $ L _ {0} = L _ {0} ^ {*} $, and $ L _ {0} ^ \prime $ is said to be essentially self-adjoint. Any of the following conditions are sufficient for $ L _ {0} ^ \prime $ to be essentially self-adjoint on $ L _ {2} ( \mathbf R ^ {n} ) $: The formally self-adjoint differential operator $ l ( x , D ) $ has the form
$$ \tag{5 } - \sum _ {k , j = 1 } ^ { n } D _ {k} a _ {kj} ( x) D _ {j} + q ( x) ,\ x \in \mathbf R ^ {n} , $$
with real coefficients, and $ L _ {0} ^ \prime $ is bounded from below; it has the form (5), is elliptic, the $ a _ {kj} $ are constants, and $ q ( x) \geq - Q ( | x | ) $, where $ Q ( r) $ does not decrease monotonically, while the integral
$$ \int\limits ^ \infty Q ^ {-} 1/2 ( r) d r = \infty ; $$
it has constant real coefficients; it has bounded coefficients and the principal part is of elliptic type with real constant coefficients (cf. Principal part of a differential operator).
Let $ L _ {0} $ have finite deficiency indices $ n _ \pm = \mathop{\rm dim} H _ \pm $, which is typical for ordinary differential operators. In this case the numbers $ n _ \pm $ coincide with the dimensions of the subspaces of solutions of the equations $ l ( u) = \pm i u $ in $ L _ {2} ( a , b ) $. Therefore $ n _ \pm < m $, and the calculation of the deficiency indices of a differential operator is connected with the qualitative theory and asymptotic methods of ordinary differential equations.
Let $ n = 1 $ and $ x \in ( a , b ) $. If $ n _ {+} \neq n _ {-} $, then $ L _ {0} ^ \prime $ does not even have one self-adjoint extension. If $ n _ {+} = n _ {-} = k $, then for the self-adjointness of extensions of $ L _ {0} ^ \prime $ it is necessary to give $ k $ boundary conditions, and these have been completely described. Boundary value problems take a simple form when the expression $ L _ {0} ^ \prime $ has two regular end-points, or has one regular end-point but $ m = 2 k $ and $ n _ \pm = k $. An end-point $ a $ is called regular if $ a > - \infty $ and $ 1 / a _ {m} ( x) $, $ a _ {j} ( x) $, $ 0 \leq j \leq m - 1 $, are summable on $ [ a , \beta ] $ for any $ \beta < b $.
There are examples of partial differential operators on $ L _ {2} ( \mathbf R ^ {n} ) $, $ n \geq 3 $, with discontinuous coefficients and with finite deficiency indices, but their theory is still underdeveloped. Not all self-adjoint extensions of symmetric partial differential operators in a bounded domain have been described in terms of boundary conditions, but various extensions with given properties have been described.
Let $ l $ be a formally self-adjoint elliptic differential operator of even order $ m = 2 k $ with real coefficients, and let $ C _ {k} ^ \infty ( \Omega _ {n} ) $ be the set of all functions having derivatives of arbitrary order in the bounded closed domain $ \overline \Omega \; _ {n} $ and satisfying Dirichlet-type boundary conditions $ D ^ \alpha u = 0 $, $ x \in \Gamma $, $ | \alpha | \leq k - 1 $. Then the differential operator defined by $ l $ with domain of definition $ C _ {k} ^ \infty ( \Omega _ {n} ) $ is symmetric, and its closure $ L _ {m} $ is self-adjoint. There are other examples of concrete self-adjoint boundary conditions for differential operators. Most complete studies have been made in the case of second-order differential operators with boundary conditions of Dirichlet-type, von Neumann-type or of the third kind.
Spectral analysis of self-adjoint differential operators.
Every self-adjoint differential operator $ L $ admits a spectral decomposition of the form
$$ \tag{6 } L = \int\limits _ {- \infty } ^ { {+ } \infty } \lambda d E _ \lambda , $$
where $ E _ \lambda $ is a resolution of the identity (into an orthogonal family of projectors). However, the general formula does not give a direct expansion with respect to the eigenfunctions of a concrete self-adjoint differential operator, and so it is important to be able to express the family $ E _ \lambda $ in terms of eigenfunctions. If a self-adjoint differential operator $ L $ has discrete spectrum $ \{ \lambda _ {k} \} $ with corresponding orthonormalized eigenfunctions $ \{ \phi _ {k} ( x) \} $, then $ E _ \lambda $ is an integral operator with (spectral) kernel
$$ \tag{7 } E ( x , y , \lambda ) = \ \sum _ {\lambda _ {k} \in ( 0 , \lambda ] } \phi _ {k} ( x) \overline{ {\phi _ {k} ( y ) }}\; . $$
In the case of a continuous spectrum of a differential operator, the question becomes complicated: For continuous spectra there are no eigenfunctions in $ L _ {2} ( \Omega _ {n} ) $. However, the following results are true.
Let $ L $ be an ordinary self-adjoint differential operator of the form (1) on $ L _ {2} ( - \infty , \infty ) $, and let $ \phi _ {1} ( x , \lambda ) \dots \phi _ {m} ( x , \lambda ) $ be a fundamental system of solutions of the equations $ l u = \lambda u $. Then there is a monotone matrix function $ \sigma ( \lambda ) = \| \sigma _ {ij} ( \lambda ) \| _ {i , j = 1 } ^ {m} $( a spectral measure) such that the resolution of the identity $ E _ \lambda $ of $ L $ is given by the kernel
$$ \tag{8 } E ( x , y , \lambda ) = \int\limits _ { 0 } ^ \lambda \sum _ {i , j = 1 } ^ { m } \phi _ {i} ( x , \lambda ) {\phi _ {j} ( y , \lambda ) } bar d \sigma _ {ij} ( \lambda ) . $$
Moreover, for any function $ f $ in $ L _ {2} ( - \infty , \infty ) $ the integral
$$ \tag{9 } \{ F _ {j} ( \lambda ) \} = \ \left \{ \int\limits _ {- \infty } ^ { {+ } \infty } \overline{ {\phi _ {j} ( x , \lambda ) }}\; f ( x) d x \right \} $$
converges in the space of vector functions $ L _ {2} ( - \infty , \infty ; d \sigma ( \lambda ) ) $ generated by the measure $ \sigma ( \lambda ) $, and, conversely, the integral
$$ \int\limits _ {- \infty } ^ { {+ } \infty } \ \sum _ {i , j = 1 } ^ { m } F _ {i} ( \lambda ) \phi _ {j} ( x , \lambda ) d \sigma _ {ij} ( \lambda ) $$
converges to $ f ( x) $ in $ L _ {2} ( - \infty , \infty ) $. If (1) has a regular end-point $ a $ and $ m = 2 k $, and the deficiency indices $ n _ \pm = k $, then the functions $ \phi _ {1} ( x , \lambda ) \dots \phi _ {k} ( x , \lambda ) $ can be chosen to form a fundamental system in the class of solutions of the equation $ l u = \lambda u $ satisfying boundary conditions at $ a $, and in this case the order of the spectral measure is equal to $ k $.
Let $ L $ be a self-adjoint elliptic differential operator on $ L _ {2} ( \Omega _ {n} ) $. Then its resolution of the identity $ E $ is an integral operator with kernel $ E ( x , y , \lambda ) $, and there is a non-decreasing function $ \rho ( \lambda ) $ such that for all numbers $ \lambda _ {1} $ and $ \lambda _ {2} $,
$$ \tag{10 } E ( x , y , \lambda _ {1} ) - E ( x , y , \lambda _ {2} ) = \ \int\limits _ { \lambda _ {1} } ^ { {\lambda _ 2 } } \phi ( x , y , \lambda ) d \rho ( \lambda ) , $$
where, for every $ \lambda $, there is a finite or infinite system $ \{ \phi _ {j} ( x , \lambda ) \} $ of solutions of the equation $ l u = \lambda u $ and
$$ \tag{11 } \phi ( x , y , \lambda ) = \ \sum _ { j } \phi _ {j} ( x , \lambda ) \overline{ {\phi _ {j} ( y , \lambda ) }}\; . $$
For the Schrödinger operator $ L u = - \Delta u + q ( x) u $, $ x \in \mathbf R ^ {3} $, under the condition $ | q ( x) | \leq c ( 1 + | x | ) ^ {- 2 - \epsilon } $, the kernel $ E ( x , y , \lambda ) $ can be explicitly expressed in terms of the solutions of the dispersion equation.
The formulas (10), (11) also hold for arbitrary self-adjoint partial differential operators, and in this case the $ \{ \phi _ {j} ( x , \lambda ) \} $ may be generalized functions, but they are of finite order.
The nature of the convergence of the expansion into eigenfunctions and the asymptotic properties of the spectral kernel help to justify the Fourier method for solving the equations of mathematical physics. For ordinary differential operators, there is the following final result, the so-called equiconvergence theorem: The expansion of a given summable function into the eigenfunctions of a differential operator which is bounded from below and the Fourier integral are both convergent or both divergent (i.e. equi-convergent) at any point. For partial differential operators, the question becomes complicated.
Qualitative theory of the spectrum of a differential operator.
This theory is concerned with the study of the nature of the spectrum in relation to the behaviour of the coefficients, the geometry of the domain and the boundary conditions.
There is a series of tests for the discreteness of the spectrum of a differential operator. The most general are the following criterion and its generalizations: If $ q ( x) \geq 1 $, then the spectrum of the differential operator generated by the expression $ l u = - u ^ {\prime\prime} + q ( x ) u $ on $ L _ {2} ( - \infty , \infty ) $ is discrete if and only if for any $ j > 0 $,
$$ \lim\limits _ {| x | \rightarrow \infty } \ \int\limits _ { x } ^ { {x } + j } q ( t) d t = \infty . $$
The generalization of this criterion to partial differential operators takes a more complicated form. There are other, simpler, tests for discreteness of the spectrum of a differential operator. For example, the self-adjoint differential operator generated by (5) has discrete spectrum if $ q ( x) \rightarrow \infty $ as $ | x | \rightarrow \infty $. The self-adjoint differential operator $ L _ {m} $ has discrete spectrum.
The study of the nature of a spectrum when there is a continuous part is a difficult problem. Here are some results: 1) if an ordinary differential operator is defined by a formally self-adjoint expression (1) with periodic coefficients on $ ( - \infty , \infty ) $ having a common period, then its spectrum is continuous and consists of a sequence of disjoint intervals whose end-points tend to $ - \infty $ or $ + \infty $; 2) if a differential operator is defined by the expression $ ( - 1 ) ^ {k} ( D _ {1} ^ {2} + \dots + D _ {n} ^ {2} ) ^ {k} + q ( x ) $ on $ L _ {2} ( \mathbf R ^ {n} ) $ and $ \lim\limits q ( x) = 0 $ as $ | x | \rightarrow + \infty $, then its continuous spectrum fills $ [ 0 , \infty ] $, while its negative spectrum is discrete and can have a limit point at zero only. If $ k = 1 $, $ | q ( x) | \leq M ( | x | ) $ and
$$ \int\limits ^ \infty r M ( r) d r < \infty \ \ ( M ( r) = O ( r ^ {-} 1 ) ) , $$
then the negative spectrum is finite (there are no eigenvalues in the continuous spectrum).
The nature of the spectrum also depends on the boundary conditions. In a bounded domain, concrete boundary conditions have been described whose fulfillment guarantees that the spectrum of a self-adjoint Laplace operator has a continuous part. This is a consequence of the deficiency indices of the minimal Laplace operator being infinite in a domain with boundary.
Functions of a self-adjoint differential operator.
These are studied with the aim of solving mixed problems for differential equations, and also for problems in the theory of differential operators. Let $ l $ be an elliptic differential operator of order $ m $. The resolvent $ ( L + \lambda ) ^ {-} 1 $ when $ \lambda > 0 $, and the functions $ \mathop{\rm exp} ( - L t ) $ and $ \mathop{\rm exp} ( i L ^ {1/m} t ) $ when $ t > 0 $, have been thoroughly studied. The latter are solution operators for the generalized heat equation $ u _ {t} = - L u $, $ u ( 0 , x ) = f ( x) $, and the generalized wave equation $ u _ {t} = i L ^ {1/m} u $, $ u ( 0 , x ) = f ( x) $, respectively. All three operator-functions are integral functions, and have kernels $ R ( x , y , \lambda ) $, $ K ( x , y , \lambda ) $, $ G ( x , y , t ) $( Green functions), respectively. The formula
$$ \tag{12 } R ( x , y , \lambda ) = \int\limits _ { 0 } ^ \infty e ^ {- \lambda t } K ( x , y , t ) d t $$
establishes a connection between $ R $ and $ K $. Some properties of $ R ( x , y , \lambda ) $ are: If $ L $ is an elliptic self-adjoint differential operator of order $ m $ on $ L _ {2} ( \Omega _ {n} ) $, then to $ ( L + \lambda ) ^ {-} p $ there corresponds a kernel of Carleman type when $ p > n / 2 m $; when $ p > n / m $, $ ( L _ {m} + \lambda ) ^ {-} p $ is nuclear, and therefore
$$ \tag{13 } S _ {p} ( L + \lambda ) ^ {-} p = \ \sum _ { k= } 1 ^ \infty ( \lambda _ {k} + \lambda ) ^ {-} p , $$
where $ \{ \lambda _ {k} \} $ are the eigenvalues of $ L _ {m} $. There are also other tests of nuclearity for $ ( L + \lambda ) ^ {-} p $ on $ L _ {2} ( \mathbf R ^ {n} ) $.
The analytic and asymptotic properties of Green functions give useful information about the spectral nature of a differential operator $ L $. For example, if in (13) the behaviour of $ S _ {p} ( L + \lambda ) ^ {-} p $ as $ \lambda \rightarrow \infty $ is known, then the application of Tauberian theorems enables one to find the asymptotics of $ \lambda _ {k} $. The same can be done if one knows the asymptotics of $ S _ {p} \mathop{\rm exp} ( - L t ) $ as $ t \rightarrow + 0 $. The asymptotics of $ R ( x , y , \lambda ) $ and $ K ( x , y , \lambda ) $ can be established, for example, by the method of parametrics, by the method of potentials, etc. The asymptotics of $ \lambda _ {k} $ have thus been found for an extensive class of elliptic differential operators. To determine the asymptotics of the spectral kernel $ E ( x , y , \lambda ) $ of an elliptic differential operator, the study of the asymptotics of the kernel $ G ( x , y , t ) $ as $ t \rightarrow 0 $ has proved effective in conjunction with subsequent application of various Tauberian theorems. In particular, when $ x = y $, $ x \notin \Gamma $,
$$ E ( x , x , \lambda ) = ( 2 \pi ) ^ {-} n \int\limits _ {l _ {0} ( x , \xi ) < \lambda } \ d \xi + O ( \lambda ^ {( n - 1 ) / m } ) . $$
Non-self-adjoint differential operators.
Most complete results have been obtained for ordinary differential operators on a finite interval. Let $ L $ be the differential operator defined by (1) when $ n = 1 $ and $ a _ {m} ( x) \equiv 1 $ on functions having $ m - 1 $ absolutely-continuous derivatives and satisfying the boundary conditions:
$$ l _ { \nu _ {0} } ( u) + l _ {\nu _ {1} } ( u) \equiv \alpha _ \nu u ^ {( k _ \nu ) } ( 0) + \sum _ { j= } 0 ^ { {k _ \nu } - 1 } \alpha _ {\nu _ {j} } u ^ {(} j) ( 0) + $$
$$ + \beta _ \nu u ^ {( k _ \nu ) } ( 1) + \sum _ { j= } 0 ^ { { } k _ \nu - 1 } \beta _ {\nu _ {j} } u ^ {(} j) ( 1) = 0 ,\ 1 \leq \nu \leq m . $$
Here $ m - 1 \geq k _ {1} \geq \dots \geq k _ {m} \geq 0 $, $ k _ {\nu - 2 } < k _ \nu $ and $ \alpha _ \nu , \beta _ \nu $ do not simultaneously vanish. Let the boundary conditions (2) be regular. This holds for boundary conditions of Sturm–Liouville type ( $ m = 2 k $, $ l _ {\nu 0 } ( u) = l _ {\nu 1 } ( u) = 0 $, $ 1 \leq \nu \leq m - 1 $), and also for periodic-type boundary conditions $ ( \alpha _ \nu = \beta _ \nu = 1 ) $. Then $ L $ has an infinite number of eigenvalues, which have precise asymptotics; the system consisting of the eigenfunctions of $ L $ and of their associates is complete in $ L _ {p} ( 0 , 1 ) $; the expansion of functions $ f $ in $ D ( L) $ into eigenfunctions of $ L $ and their associates converges uniformly on $ ( 0 , 1 ] $. The system of eigenfunctions and their associates may also be complete under certain non-regular boundary conditions, in particular of splitting type ( $ l _ {\nu 0 } ( u) = 0 $, $ 1 \leq \nu \leq m _ {1} $, $ l _ {\nu 1 } ( u) = 0 $, $ 1 \leq \nu = m _ {2} $, $ m _ {1} \neq m _ {2} $, $ m _ {1} + m _ {2} = m $). However, the convergence of the expansion into a series of eigenfunctions and their associates holds only for a narrow class of ( $ l $- analytic) functions.
Let $ L _ {0} $ be a self-adjoint operator on a separable Hilbert space $ H $ with eigenvalues $ \{ \lambda _ {k} \} $, and suppose that the operator $ L _ {0} ^ {-} p $ is nuclear for a certain $ p > 0 $. Let $ L _ {1} $ be another operator such that $ L _ {1} L _ {0} ^ {-} 1 $ is compact. Then the system consisting of the eigenvectors of $ L _ {0} + L _ {1} $ and of their associates is complete in $ H $( Keldysh' theorem). The application of this theorem gives classes of differential operators which have a complete system of eigenfunctions and their associates.
Let $ L _ {m} $ be a differential operator on $ L _ {2} ( \Omega _ {n} ) $ and let
$$ L _ {1} u = \sum _ {| \alpha | \leq m - 1 } d _ \alpha ( x) D ^ \alpha u . $$
Then the system consisting of the eigenfunctions of $ L _ {m} + L _ {1} $ and of their associates is complete in $ L _ {2} ( \Omega _ {n} ) $. However, the expansion of a function into a series with respect to this system is divergent, in general, and is conditionally summable by the generalized Abel method.
If $ \Omega _ {n} $ is an unbounded domain, then to satisfy the conditions of Keldysh' theorem one must impose further conditions on the growth of the coefficient functions of the differential operator.
Non-self-adjoint differential operators with a continuous part in their spectrum have not been studied much. This is connected with the fact that no analogue of the spectral decomposition theorem exists in this case. An exception is the differential operator generated by the expression $ - d ^ {2} u / d x ^ {2} + q ( x) $ where $ x \in [ 0 , \infty ) $ or $ x \in ( - \infty , \infty ) $ and $ q ( x) $ is a complex-valued function. Let $ \phi ( x , k ) $ be the solution of the equation $ - u ^ {(} 2) + q ( x ) u = k ^ {2} u $ for $ 0 \leq x < \infty $ satisfying the initial conditions $ \phi ( 0 , k ) = 1 $, $ \phi ^ \prime ( 0 , k ) = 0 $. Let $ f _ {1} $ and $ f _ {2} $ be functions in $ L _ {2} ( 0 , \infty ) $ of compact support and let
$$ F _ {j} ( k) = \int\limits _ { 0 } ^ \infty f _ {j} ( x) \phi ( x , k ) d x . $$
Then there is a linear functional $ R $ on a linear topological space $ G $ such that $ F _ {1} F _ {2} \in G $ and
$$ ( R , F _ {1} F _ {2} ) = \ \int\limits _ { 0 } ^ \infty f _ {1} ( x) f _ {2} ( x) d x . $$
The space $ G $ is the set of all even entire functions of order of growth one and of finite type that are summable on the real axis. If $ x q ( x) \in L _ {1} ( 0 , \infty ) $, then $ R $ can be explicitly calculated. In this case, spectral singularities, that is, poles of the kernel of the resolvent, appear in the continuous spectrum, and these are not eigenvalues of the differential operator. Spectral singularities are inherent in non-self-adjoint operators, and because of them, questions of the expansion into eigenfunctions (and convergence problems) become more complicated. For the differential operator
$$ L u \equiv ( - D _ {1} ^ {2} - D _ {2} ^ {2} - D _ {3} ^ {2} + q ( x) ) u $$
on $ L _ {2} ( \mathbf R ^ {3} ) $, where $ q ( x) $ is a complex-valued function that decreases exponentially, a form of spectral decomposition has also been found by solving a problem in dispersion theory, taking the influence of spectral singularities into account.
Inverse problems of spectral analysis.
These arise when one asks for the determination of differential operators by certain spectral characteristics. The problems of determining one-dimensional Schrödinger equations and systems of Dirac type have been completely solved, given the spectra of various extensions, the spectral measure, scattering data (that is, the asymptotic behaviour of normalized eigenfunctions), or other properties. Inverse problems have found applications in the integration of non-linear equations.
The spectral theory of differential operators arose in connection with investigations on vibrating strings and gave birth to the theory of orthogonal expansions (18th century and 19th century). The systematic study of self-adjoint differential operators of the second order on a finite interval dates from 1830 (the Sturm–Liouville problem) and was the subject of intensive study in the 19th century, in particular in connection with the theory of special functions. However, the completeness of the system of eigenfunctions of the Sturm–Liouville operator was not proved until 1896, when the nature of the convergence of the expansion into eigenfunctions was also investigated. The theory of singular differential operators began in 1909–1910, when the spectral decomposition of a self-adjoint unbounded differential operator of the second order with an arbitrary spectral structure was discovered, and when, in principle, the concept of a deficiency index was introduced, and the first results in the theory of extensions were obtained. Interest in singular differential operators grew from 1920 onwards, along with the rise of quantum mechanics. The systematic investigation of non-self-adjoint singular differential operators began in 1950, when the foundations of the theory of operator pencils were expounded and a method was found for proving the completeness of the system consisting of the eigenfunctions of a differential operator and of their associates.
References
| [1] | Yu.M. [Yu.M. Berezanskii] Berezanskiy, "Expansion in eigenfunctions of selfadjoint operators" , Amer. Math. Soc. (1968) (Translated from Russian) |
| [2] | I.M. Glazman, "Direct methods of qualitative spectral analysis of singular differential operators" , Israel Program Sci. Transl. (1965) (Translated from Russian) MR0190800 Zbl 0143.36505 |
| [3] | N. Dunford, J.T. Schwartz, "Linear operators. Spectral theory" , 2 , Interscience (1963) MR0188745 |
| [4] | T. Kato, "Perturbation theory for linear operators" , Springer (1976) MR0407617 Zbl 0342.47009 |
| [5] | B.M. Levitan, I.S. Sargsyan, "Introduction to spectral theory: selfadjoint ordinary differential operators" , Amer. Math. Soc. (1975) (Translated from Russian) MR0369797 Zbl 0302.47036 |
| [6] | V.A. Marchenko, "Sturm–Liouville operators and applications" , Birkhäuser (1986) (Translated from Russian) MR0897106 Zbl 0592.34011 |
| [7] | M.A. Naimark, "Linear differential operators" , 1–2 , F. Ungar (1967–1968) (Translated from Russian) MR2814127 MR0353061 MR0262880 MR0216050 MR0067292 MR0050109 Zbl 1221.47085 Zbl 0227.34020 Zbl 0219.34001 Zbl 0057.07102 |
| [8] | E.C. Titchmarsh, "Eigenfunction expansions associated with second-order differential equations" , 1 , Clarendon Press (1962) pp. Chapts. 1; 2 MR0176151 Zbl 0099.05201 |
| [9a] | L.D. Faddeev, "Mathematical aspects of the three-body problem in the quantum scattering theory" , Israel Program Sci. Transl. (1965) (Translated from Russian) MR0221828 Zbl 0131.43504 |
| [9b] | L.D. Faddeev, "Properties of the 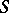 -matrix of the one-dimensional Schrödinger equation" Trudy. Mat. Inst. Steklov. , 73 (1964) pp. 314–336 (In Russian) MR178188 -matrix of the one-dimensional Schrödinger equation" Trudy. Mat. Inst. Steklov. , 73 (1964) pp. 314–336 (In Russian) MR178188 |
| [10a] | Sh.A. Alimov, V.A. Il'in, E.M. Nikishin, "Convergence problems of multiple trigonometric series and spectral decompositions I" Russian Math. Surveys , 31 : 6 (1976) pp. 29–86 Uspekhi Mat. Nauk , 31 : 6 (1976) pp. 28–83 Zbl 0367.42008 |
| [10b] | Sh.A. Alimov, V.A. Il'in, E.M. Nikishin, "Problems of convergence of multiple trigonometric series and spectral decompositions II" Russian Math. Surveys , 32 : 1 (1977) pp. 115–139 Uspekhi Mat. Nauk , 32 : 1 (1977) pp. 107–130 Zbl 0376.42002 |
| [11] | Yu.M. Berezanskii, "Self-conjugate elliptic operators with singular potential" Ukr. Math. J. , 26 : 5 (1974) pp. 475–483 Ukrain. Mat. Zh. , 26 : 5 (1974) pp. 579–590 MR352725 |
| [12] | M.G. Gasymov, "The inverse scattering problem for a system of Dirac equations of order 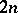 " Trans. Moscow Math. Soc. , 19 (1968) pp. 41–120 Trudy Moskov. Mat. Obshch. , 19 (1968) pp. 41–112 MR0208944 Zbl 0197.26102 " Trans. Moscow Math. Soc. , 19 (1968) pp. 41–120 Trudy Moskov. Mat. Obshch. , 19 (1968) pp. 41–112 MR0208944 Zbl 0197.26102 |
| [13] | B.M. Levitan, M.G. Gasymov, "Determination of a differential equation by two of its spectra" Russian Math. Surveys , 19 : 2 (1964) pp. 1–63 Uspekhi Mat. Nauk , 19 : 2 (1964) pp. 3–63 MR162996 Zbl 0145.10903 |
| [14] | B.A. Dubrovin, V.B. Matveev, S.P. Novikov, "Non-linear equations of Korteweg–de Vries type, finite-zone linear operators, and abelian varieties" Russian Math. Surveys , 31 : 1 (1976) pp. 59–146 Uspekhi Mat. Nauk , 31 : 1 (1976) pp. 55–136 Zbl 0461.35074 |
| [15] | A.G. Kostyuchenko, "Asymptotic behavior of the spectral function of self-adjoint elliptic operators" , 4-th Math. Summer School , Kiev (1968) pp. 42–117 (In Russian) |
| [16] | L. Hörmander, "The spectral function of an elliptic operator" Acta Math. , 121 (1968) pp. 193–218 MR0609014 Zbl 0164.13201 |
Comments
An important recent development is the study of the spectral asymptotics of elliptic operators, see [a1], Chapt. XXIX, and [a4] as an introduction; cf. also [a5].
References
| [a1] | L.V. Hörmander, "The analysis of linear partial differential operators" , II, IV , Springer (1983–1985) pp. Chapts. XIV, XXIX, XXX MR2512677 MR2304165 MR2108588 MR1996773 MR1481433 MR1313500 MR1065993 MR1065136 MR0961959 MR0925821 MR0881605 MR0862624 MR1540773 MR0781537 MR0781536 MR0717035 MR0705278 Zbl 1178.35003 Zbl 1115.35005 Zbl 1062.35004 Zbl 1028.35001 Zbl 0712.35001 Zbl 0687.35002 Zbl 0619.35002 Zbl 0619.35001 Zbl 0612.35001 Zbl 0601.35001 Zbl 0521.35002 Zbl 0521.35001 |
| [a2] | M. Schechter, "Spectra of partial differential operators" , North-Holland (1971) MR0447834 Zbl 0225.35001 |
| [a3] | F. Calogero, A. Degasperis, "Nonlinear evolution equations solvable by the inverse spectral transform II" Nuovo Cimento , 39B (1977) pp. 1–54 MR0456025 |
| [a4] | M.A. Shubin, "Pseudodifferential operators and spectral theory" , Springer (1980) (Translated from Russian) MR1852334 MR0883081 MR0509034 Zbl 0980.35180 Zbl 0616.47040 Zbl 0451.47064 |
| [a5] | S. Levendorskii, "Asymptotic distribution of eigenvalues of differential operators" , Kluwer (1991) (Translated from Russian) MR1079317 |
Spectral theory of differential operators. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spectral_theory_of_differential_operators&oldid=48766