Difference between revisions of "Space with an indefinite metric"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | s0862302.png | ||
| + | $#A+1 = 138 n = 3 | ||
| + | $#C+1 = 138 : ~/encyclopedia/old_files/data/S086/S.0806230 Space with an indefinite metric, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | A pair of objects | + | {{TEX|auto}} |
| + | {{TEX|done}} | ||
| + | |||
| + | '' $ G $- | ||
| + | space'' | ||
| + | |||
| + | A pair of objects $ ( E , G ) $, | ||
| + | the first of which is a vector space $ E $ | ||
| + | over the field of complex numbers, while the second is a bilinear (more precisely, sesquilinear) form $ G $ | ||
| + | on $ E $; | ||
| + | this form is also called a $ G $- | ||
| + | metric. If $ G $ | ||
| + | is a positive-definite (a so-called definite) form, then it is a scalar product in $ E $, | ||
| + | and one can use it to canonically introduce (cf., e.g., [[Hilbert space with an indefinite metric|Hilbert space with an indefinite metric]]) a norm and a distance (i.e. an ordinary metric) for the elements of $ E $. | ||
| + | In the case of a general sesquilinear form $ G $ | ||
| + | there is neither a norm nor a metric canonically related to $ G $, | ||
| + | and the phrase "G-metric" only recalls the close relation of definite sesquilinear forms with certain metrics in vector spaces. | ||
The theory of finite-dimensional spaces with an indefinite metric, more often called bilinear metric spaces, or spaces with a bilinear metric, was developed already by G. Frobenius, and is expounded in courses on linear algebra (cf. [[#References|[1]]]). | The theory of finite-dimensional spaces with an indefinite metric, more often called bilinear metric spaces, or spaces with a bilinear metric, was developed already by G. Frobenius, and is expounded in courses on linear algebra (cf. [[#References|[1]]]). | ||
| Line 9: | Line 32: | ||
The theory of spaces with an indefinite metric has been developed in two directions — their geometry and linear operations on them. | The theory of spaces with an indefinite metric has been developed in two directions — their geometry and linear operations on them. | ||
| − | In the geometry of spaces with an indefinite metric one basically studies: a) the relation between the | + | In the geometry of spaces with an indefinite metric one basically studies: a) the relation between the $ G $- |
| + | metric and various topologies on $ E $; | ||
| + | b) the classification of vector subspaces (linear manifolds) in $ E $ | ||
| + | relative to the $ G $- | ||
| + | metric (especially, the so-called definite subspaces, see below); c) the properties of $ G $- | ||
| + | projections; and d) bases of $ G $- | ||
| + | spaces. | ||
| − | In the case of a Hermitian | + | In the case of a Hermitian $ G $- |
| + | metric (a $ G ^ {H} $- | ||
| + | metric), i.e. such that $ G ( x , y ) = \overline{ {G ( y , x ) }}\; $ | ||
| + | for all $ x , y \in E $, | ||
| + | the most important results and concepts in the geometry of spaces with an indefinite metric are as follows. Suppose that each vector $ y \in E $ | ||
| + | is put in correspondence with a linear functional $ G _ {y} : x \rightarrow G ( x , y ) $, | ||
| + | $ x \in E $. | ||
| + | A topology $ \tau $ | ||
| + | on $ E $ | ||
| + | is called subordinate to the $ G $- | ||
| + | metric if $ G _ {y} $ | ||
| + | is continuous in $ \tau $ | ||
| + | for all $ y \in E $; | ||
| + | $ \tau $ | ||
| + | is called compatible with the $ G $- | ||
| + | metric if it is subordinate to $ G $ | ||
| + | and if every $ \tau $- | ||
| + | continuous functional has the form $ G _ {y} $, | ||
| + | $ y \in E $. | ||
| + | In a space $ E $ | ||
| + | with an indefinite metric one cannot specify more than one Fréchet topology subordinate to $ G $, | ||
| + | and not every $ G $- | ||
| + | metric allows such a topology (cf. [[#References|[4]]]). If a topology, subordinate to the $ G $- | ||
| + | metric, is a pre-Hilbert topology on $ E $ | ||
| + | and is given by a scalar product $ H ( \cdot , \cdot ) $ | ||
| + | in $ E $, | ||
| + | then $ H $ | ||
| + | is called a Hermitian non-negative majorant of $ G $; | ||
| + | in this case | ||
| − | + | $$ | |
| + | | G ( x , y ) | ^ {2} \leq CH ( x , x ) H ( y , y ) ,\ \ | ||
| + | C = \textrm{ const } ,\ \ | ||
| + | x , y \in E . | ||
| + | $$ | ||
| − | After completing in the | + | After completing in the $ H $- |
| + | norm one obtains a Hilbert space with indefinite metric $ ( \widetilde{E} , \widetilde{G} ) $, | ||
| + | where $ \widetilde{G} $ | ||
| + | is the continuous extension of $ G $ | ||
| + | to the entire space $ \widetilde{E} $. | ||
| + | Here, $ \widetilde{G} $ | ||
| + | may turn out to be a degenerate metric, even if $ G $ | ||
| + | is non-degenerate. This degeneration does not occur if $ G $ | ||
| + | is a non-degenerate metric and if the largest of the dimensions $ \kappa $ | ||
| + | of the positive subspaces of $ E $ | ||
| + | is finite. In the latter case one obtains the Pontryagin space $ \Pi _ \kappa $. | ||
| − | A subspace | + | A subspace $ L $ |
| + | in a space $ ( E , G ) $ | ||
| + | with an indefinite metric is called a positive subspace, a negative subspace (a more general name is: a definite subspace) or a neutral subspace, depending on whether $ G ( x , x ) > 0 $, | ||
| + | $ G ( x , x ) < 0 $ | ||
| + | or $ G ( x , x ) = 0 $ | ||
| + | for all $ x \in L $. | ||
| + | A subspace is called maximally positive if it is positive and cannot be extended with preservation of this property. Every subspace of the type indicated above is contained in a maximal subspace of the same type. | ||
| − | An important part in the classification of subspaces in spaces with an indefinite metric is played by the notions of a canonical decomposition and a | + | An important part in the classification of subspaces in spaces with an indefinite metric is played by the notions of a canonical decomposition and a $ G $- |
| + | orthogonal projection. | ||
| − | A vector | + | A vector $ x \in E $ |
| + | is called $ G $- | ||
| + | orthogonal to a subspace $ L \subset E $( | ||
| + | is isotropic with respect to $ L $) | ||
| + | if $ G ( x , y ) = 0 $ | ||
| + | for all $ y \in L $. | ||
| + | A subspace $ L $ | ||
| + | is called degenerate if it contains at least one non-zero vector that is isotropic with respect to $ L $. | ||
| − | If | + | If $ L $ |
| + | is a subspace in a space $ E $ | ||
| + | with an indefinite metric, then $ L ^ \prime = \{ {y } : {G ( x , y ) = 0 \textrm{ for all } x \in L } \} $ | ||
| + | is its $ G $- | ||
| + | orthogonal complement. Always $ L ^ {\prime\prime} = L ^ \tau $, | ||
| + | where $ \tau $ | ||
| + | is any topology compatible with $ G $. | ||
| + | The $ G $- | ||
| + | orthogonal complement $ L ^ \prime $ | ||
| + | of a degenerate vector subspace $ L $ | ||
| + | is a degenerate vector subspace that is closed in a topology $ \tau $ | ||
| + | compatible with $ G $, | ||
| + | and $ L \cap L ^ \prime $ | ||
| + | is the vector subspace of isotropic elements. A subspace $ L $ | ||
| + | is called projection complete if each $ y \in E $ | ||
| + | has a $ G $- | ||
| + | projection on $ L $, | ||
| + | i.e. if there is an $ y _ {0} \in L $ | ||
| + | for which $ G ( x , y - y _ {0} ) = 0 $ | ||
| + | for every $ x \in L $. | ||
| + | Uniqueness of a $ G $- | ||
| + | projection on $ L $ | ||
| + | is equivalent with $ L $ | ||
| + | being a non-degenerate subspace, while its existence depends on the continuity of the functional $ G _ {y} $ | ||
| + | in topologies on $ L $ | ||
| + | compatible with $ G $. | ||
| + | If $ N $ | ||
| + | and $ M $ | ||
| + | are $ G $- | ||
| + | orthogonal subspaces and $ M + N = E $, | ||
| + | then $ M $ | ||
| + | and $ N $ | ||
| + | are projection complete; if $ L $ | ||
| + | is a projection-complete subspace, then $ L + L ^ \prime = E $; | ||
| + | the sum is the direct sum if $ E $ | ||
| + | is a non-degenerate space with an indefinite metric. | ||
| − | Suppose that | + | Suppose that $ L $ |
| + | is a definite subspace in a space with an indefinite metric $ E $. | ||
| + | It is called regular if every functional $ G _ {y} $, | ||
| + | $ y \in E $, | ||
| + | is continuous on $ E $ | ||
| + | in the norm $ \| x \| _ {G} = | G ( x , x ) | ^ {1/2 } $. | ||
| + | Otherwise it is called singular. Every non-degenerate infinite-dimensional space with an indefinite metric contains singular subspaces. A definite subspace $ L $ | ||
| + | is projection complete if and only if it is regular and if for every $ y \in E $ | ||
| + | there is an $ x \in L $ | ||
| + | such that | ||
| − | + | $$ | |
| + | \| x \| _ {G} ^ {2} = \| G _ {y} \| _ {G} ^ {2} = G ( x , y ) . | ||
| + | $$ | ||
Linear operators in spaces with an indefinite metric have been studied mainly in Hilbert spaces with an indefinite metric; for Banach analogues there is a survey in [[#References|[8]]]. | Linear operators in spaces with an indefinite metric have been studied mainly in Hilbert spaces with an indefinite metric; for Banach analogues there is a survey in [[#References|[8]]]. | ||
| − | As in the case of Hilbert spaces with an indefinite metric, an important tool in the study of the geometry of spaces with an indefinite metric and of linear operators in spaces | + | As in the case of Hilbert spaces with an indefinite metric, an important tool in the study of the geometry of spaces with an indefinite metric and of linear operators in spaces $ ( E , G ) $ |
| + | endowed with some topology compatible with $ G $, | ||
| + | are the so-called $ G $- | ||
| + | orthogonal bases in $ E $, | ||
| + | i.e. bases $ \{ e _ {n} \} $ | ||
| + | of the topological vector space $ E $ | ||
| + | for which $ G( e _ {k} , e _ {n} ) = \pm \delta _ {kn} $, | ||
| + | $ k , n = 1 , 2 , . . . $( | ||
| + | cf. [[#References|[4]]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.I. Mal'tsev, "Foundations of linear algebra" , Freeman (1963) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> L.S. Pontryagin, "Hermitian operators in spaces with indefinite metric" ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''8''' (1944) pp. 243–280 (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I.S. Iokhvidov, M.G. Krein, "Spectral theory in spaces with an indefinite metric I" ''Transl. Amer. Math. Soc.'' , '''13''' (1960) pp. 105–176 ''Trudy Moskov. Mat. Obshch.'' , '''5''' (1956) pp. 367–432</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> Yu.P. Ginzburg, I.S. Iokhvidov, "The geometry of infinite-dimensional spaces with a bilinear metric" ''Russian Math. Surveys'' , '''17''' : 4 (1962) pp. 1–51 ''Uspekhi Mat. Nauk'' , '''17''' : 4 (1962) pp. 3–56</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> M.G. Krein, "Introduction to the geometry of indefinite <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086230/s086230140.png" />-spaces and the theory of operators in these spaces" , ''Second Math. Summer School'' , '''1''' , Kiev (1965) pp. 15–92 (In Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> T.Ya. Azizov, I.S. Iokhvidov, "Linear operators in Hilbert spaces with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086230/s086230141.png" />-metric" ''Russian Math. Surveys'' , '''26''' : 4 (1971) pp. 45–97 ''Uspekhi Mat. Nauk'' , '''26''' : 4 (1971) pp. 43–92</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> K.L. Nagy, "State vector spaces with indefinite metric in quantum field theory" , Noordhoff (1966)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> I.S. Iokhvidov, "Banach spaces with a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086230/s086230142.png" />-metric and certain classes of linear operators in these spaces" ''Izv. Akad. Nauk MoldavSSR'' , '''1''' (1968) pp. 60–80 (In Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.I. Mal'tsev, "Foundations of linear algebra" , Freeman (1963) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> L.S. Pontryagin, "Hermitian operators in spaces with indefinite metric" ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''8''' (1944) pp. 243–280 (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I.S. Iokhvidov, M.G. Krein, "Spectral theory in spaces with an indefinite metric I" ''Transl. Amer. Math. Soc.'' , '''13''' (1960) pp. 105–176 ''Trudy Moskov. Mat. Obshch.'' , '''5''' (1956) pp. 367–432</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> Yu.P. Ginzburg, I.S. Iokhvidov, "The geometry of infinite-dimensional spaces with a bilinear metric" ''Russian Math. Surveys'' , '''17''' : 4 (1962) pp. 1–51 ''Uspekhi Mat. Nauk'' , '''17''' : 4 (1962) pp. 3–56</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> M.G. Krein, "Introduction to the geometry of indefinite <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086230/s086230140.png" />-spaces and the theory of operators in these spaces" , ''Second Math. Summer School'' , '''1''' , Kiev (1965) pp. 15–92 (In Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> T.Ya. Azizov, I.S. Iokhvidov, "Linear operators in Hilbert spaces with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086230/s086230141.png" />-metric" ''Russian Math. Surveys'' , '''26''' : 4 (1971) pp. 45–97 ''Uspekhi Mat. Nauk'' , '''26''' : 4 (1971) pp. 43–92</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> K.L. Nagy, "State vector spaces with indefinite metric in quantum field theory" , Noordhoff (1966)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> I.S. Iokhvidov, "Banach spaces with a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086230/s086230142.png" />-metric and certain classes of linear operators in these spaces" ''Izv. Akad. Nauk MoldavSSR'' , '''1''' (1968) pp. 60–80 (In Russian)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | A topology | + | A topology $ \tau $ |
| + | that is compatible with the $ G $- | ||
| + | metric is also called an admissible topology. For an admissible topology, $ L ^ \tau $ | ||
| + | denotes the $ \tau $- | ||
| + | closure of $ L $ | ||
| + | in $ E $. | ||
| + | The $ G $- | ||
| + | orthogonal complement is called the orthogonal companion in [[#References|[a2]]]. The weak topology on the $ G $- | ||
| + | space $ E $ | ||
| + | is the locally convex topology defined by the family of semi-norms (cf. [[Semi-norm|Semi-norm]]) | ||
| − | + | $$ | |
| + | p _ {y} ( x) = | G ( x , y) | . | ||
| + | $$ | ||
| − | It is an admissible topology, and the weakest such. As a consequence of the double orthogonal complement theorem, | + | It is an admissible topology, and the weakest such. As a consequence of the double orthogonal complement theorem, $ L ^ {\prime\prime} = L ^ \tau $, |
| + | one thus has that $ L ^ {\prime\prime} = L $ | ||
| + | if and only if $ L $ | ||
| + | is weakly closed. | ||
For additional information about spaces with an indefinite metric see [[Krein space|Krein space]] and [[#References|[a1]]]–[[#References|[a4]]]. | For additional information about spaces with an indefinite metric see [[Krein space|Krein space]] and [[#References|[a1]]]–[[#References|[a4]]]. | ||
Latest revision as of 08:22, 6 June 2020
$ G $-
space
A pair of objects $ ( E , G ) $, the first of which is a vector space $ E $ over the field of complex numbers, while the second is a bilinear (more precisely, sesquilinear) form $ G $ on $ E $; this form is also called a $ G $- metric. If $ G $ is a positive-definite (a so-called definite) form, then it is a scalar product in $ E $, and one can use it to canonically introduce (cf., e.g., Hilbert space with an indefinite metric) a norm and a distance (i.e. an ordinary metric) for the elements of $ E $. In the case of a general sesquilinear form $ G $ there is neither a norm nor a metric canonically related to $ G $, and the phrase "G-metric" only recalls the close relation of definite sesquilinear forms with certain metrics in vector spaces.
The theory of finite-dimensional spaces with an indefinite metric, more often called bilinear metric spaces, or spaces with a bilinear metric, was developed already by G. Frobenius, and is expounded in courses on linear algebra (cf. [1]).
The main purpose of the general theory of spaces with an indefinite metric is the separation and study of relatively simple, but for applications important, classes of non-self-adjoint operators in a Hilbert space (cf. Non-self-adjoint operator). Spaces with an indefinite metric were for the first time introduced by L.S. Pontryagin [2] (for more detail, see Pontryagin space).
The theory of spaces with an indefinite metric has been developed in two directions — their geometry and linear operations on them.
In the geometry of spaces with an indefinite metric one basically studies: a) the relation between the $ G $- metric and various topologies on $ E $; b) the classification of vector subspaces (linear manifolds) in $ E $ relative to the $ G $- metric (especially, the so-called definite subspaces, see below); c) the properties of $ G $- projections; and d) bases of $ G $- spaces.
In the case of a Hermitian $ G $- metric (a $ G ^ {H} $- metric), i.e. such that $ G ( x , y ) = \overline{ {G ( y , x ) }}\; $ for all $ x , y \in E $, the most important results and concepts in the geometry of spaces with an indefinite metric are as follows. Suppose that each vector $ y \in E $ is put in correspondence with a linear functional $ G _ {y} : x \rightarrow G ( x , y ) $, $ x \in E $. A topology $ \tau $ on $ E $ is called subordinate to the $ G $- metric if $ G _ {y} $ is continuous in $ \tau $ for all $ y \in E $; $ \tau $ is called compatible with the $ G $- metric if it is subordinate to $ G $ and if every $ \tau $- continuous functional has the form $ G _ {y} $, $ y \in E $. In a space $ E $ with an indefinite metric one cannot specify more than one Fréchet topology subordinate to $ G $, and not every $ G $- metric allows such a topology (cf. [4]). If a topology, subordinate to the $ G $- metric, is a pre-Hilbert topology on $ E $ and is given by a scalar product $ H ( \cdot , \cdot ) $ in $ E $, then $ H $ is called a Hermitian non-negative majorant of $ G $; in this case
$$ | G ( x , y ) | ^ {2} \leq CH ( x , x ) H ( y , y ) ,\ \ C = \textrm{ const } ,\ \ x , y \in E . $$
After completing in the $ H $- norm one obtains a Hilbert space with indefinite metric $ ( \widetilde{E} , \widetilde{G} ) $, where $ \widetilde{G} $ is the continuous extension of $ G $ to the entire space $ \widetilde{E} $. Here, $ \widetilde{G} $ may turn out to be a degenerate metric, even if $ G $ is non-degenerate. This degeneration does not occur if $ G $ is a non-degenerate metric and if the largest of the dimensions $ \kappa $ of the positive subspaces of $ E $ is finite. In the latter case one obtains the Pontryagin space $ \Pi _ \kappa $.
A subspace $ L $ in a space $ ( E , G ) $ with an indefinite metric is called a positive subspace, a negative subspace (a more general name is: a definite subspace) or a neutral subspace, depending on whether $ G ( x , x ) > 0 $, $ G ( x , x ) < 0 $ or $ G ( x , x ) = 0 $ for all $ x \in L $. A subspace is called maximally positive if it is positive and cannot be extended with preservation of this property. Every subspace of the type indicated above is contained in a maximal subspace of the same type.
An important part in the classification of subspaces in spaces with an indefinite metric is played by the notions of a canonical decomposition and a $ G $- orthogonal projection.
A vector $ x \in E $ is called $ G $- orthogonal to a subspace $ L \subset E $( is isotropic with respect to $ L $) if $ G ( x , y ) = 0 $ for all $ y \in L $. A subspace $ L $ is called degenerate if it contains at least one non-zero vector that is isotropic with respect to $ L $.
If $ L $ is a subspace in a space $ E $ with an indefinite metric, then $ L ^ \prime = \{ {y } : {G ( x , y ) = 0 \textrm{ for all } x \in L } \} $ is its $ G $- orthogonal complement. Always $ L ^ {\prime\prime} = L ^ \tau $, where $ \tau $ is any topology compatible with $ G $. The $ G $- orthogonal complement $ L ^ \prime $ of a degenerate vector subspace $ L $ is a degenerate vector subspace that is closed in a topology $ \tau $ compatible with $ G $, and $ L \cap L ^ \prime $ is the vector subspace of isotropic elements. A subspace $ L $ is called projection complete if each $ y \in E $ has a $ G $- projection on $ L $, i.e. if there is an $ y _ {0} \in L $ for which $ G ( x , y - y _ {0} ) = 0 $ for every $ x \in L $. Uniqueness of a $ G $- projection on $ L $ is equivalent with $ L $ being a non-degenerate subspace, while its existence depends on the continuity of the functional $ G _ {y} $ in topologies on $ L $ compatible with $ G $. If $ N $ and $ M $ are $ G $- orthogonal subspaces and $ M + N = E $, then $ M $ and $ N $ are projection complete; if $ L $ is a projection-complete subspace, then $ L + L ^ \prime = E $; the sum is the direct sum if $ E $ is a non-degenerate space with an indefinite metric.
Suppose that $ L $ is a definite subspace in a space with an indefinite metric $ E $. It is called regular if every functional $ G _ {y} $, $ y \in E $, is continuous on $ E $ in the norm $ \| x \| _ {G} = | G ( x , x ) | ^ {1/2 } $. Otherwise it is called singular. Every non-degenerate infinite-dimensional space with an indefinite metric contains singular subspaces. A definite subspace $ L $ is projection complete if and only if it is regular and if for every $ y \in E $ there is an $ x \in L $ such that
$$ \| x \| _ {G} ^ {2} = \| G _ {y} \| _ {G} ^ {2} = G ( x , y ) . $$
Linear operators in spaces with an indefinite metric have been studied mainly in Hilbert spaces with an indefinite metric; for Banach analogues there is a survey in [8].
As in the case of Hilbert spaces with an indefinite metric, an important tool in the study of the geometry of spaces with an indefinite metric and of linear operators in spaces $ ( E , G ) $ endowed with some topology compatible with $ G $, are the so-called $ G $- orthogonal bases in $ E $, i.e. bases $ \{ e _ {n} \} $ of the topological vector space $ E $ for which $ G( e _ {k} , e _ {n} ) = \pm \delta _ {kn} $, $ k , n = 1 , 2 , . . . $( cf. [4]).
References
| [1] | A.I. Mal'tsev, "Foundations of linear algebra" , Freeman (1963) (Translated from Russian) |
| [2] | L.S. Pontryagin, "Hermitian operators in spaces with indefinite metric" Izv. Akad. Nauk SSSR Ser. Mat. , 8 (1944) pp. 243–280 (In Russian) |
| [3] | I.S. Iokhvidov, M.G. Krein, "Spectral theory in spaces with an indefinite metric I" Transl. Amer. Math. Soc. , 13 (1960) pp. 105–176 Trudy Moskov. Mat. Obshch. , 5 (1956) pp. 367–432 |
| [4] | Yu.P. Ginzburg, I.S. Iokhvidov, "The geometry of infinite-dimensional spaces with a bilinear metric" Russian Math. Surveys , 17 : 4 (1962) pp. 1–51 Uspekhi Mat. Nauk , 17 : 4 (1962) pp. 3–56 |
| [5] | M.G. Krein, "Introduction to the geometry of indefinite 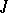 -spaces and the theory of operators in these spaces" , Second Math. Summer School , 1 , Kiev (1965) pp. 15–92 (In Russian) -spaces and the theory of operators in these spaces" , Second Math. Summer School , 1 , Kiev (1965) pp. 15–92 (In Russian) |
| [6] | T.Ya. Azizov, I.S. Iokhvidov, "Linear operators in Hilbert spaces with 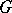 -metric" Russian Math. Surveys , 26 : 4 (1971) pp. 45–97 Uspekhi Mat. Nauk , 26 : 4 (1971) pp. 43–92 -metric" Russian Math. Surveys , 26 : 4 (1971) pp. 45–97 Uspekhi Mat. Nauk , 26 : 4 (1971) pp. 43–92 |
| [7] | K.L. Nagy, "State vector spaces with indefinite metric in quantum field theory" , Noordhoff (1966) |
| [8] | I.S. Iokhvidov, "Banach spaces with a 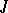 -metric and certain classes of linear operators in these spaces" Izv. Akad. Nauk MoldavSSR , 1 (1968) pp. 60–80 (In Russian) -metric and certain classes of linear operators in these spaces" Izv. Akad. Nauk MoldavSSR , 1 (1968) pp. 60–80 (In Russian) |
Comments
A topology $ \tau $ that is compatible with the $ G $- metric is also called an admissible topology. For an admissible topology, $ L ^ \tau $ denotes the $ \tau $- closure of $ L $ in $ E $. The $ G $- orthogonal complement is called the orthogonal companion in [a2]. The weak topology on the $ G $- space $ E $ is the locally convex topology defined by the family of semi-norms (cf. Semi-norm)
$$ p _ {y} ( x) = | G ( x , y) | . $$
It is an admissible topology, and the weakest such. As a consequence of the double orthogonal complement theorem, $ L ^ {\prime\prime} = L ^ \tau $, one thus has that $ L ^ {\prime\prime} = L $ if and only if $ L $ is weakly closed.
For additional information about spaces with an indefinite metric see Krein space and [a1]–[a4].
References
| [a1] | T.Ya. Azizov, I.S. [I.S. Iokhvidov] Iohidov, "Linear operators in spaces with an indefinite metric" , Wiley (1989) (Translated from Russian) |
| [a2] | J. Bognár, "Indefinite inner product spaces" , Springer (1974) |
| [a3] | I. [I. Gokhberg] Gohberg, P. Lancaster, L. Rodman, "Matrices and indefinite scalar products" , Birkhäuser (1983) |
| [a4] | I.S. [I.S. Iokhvidov] Iohidov, M.G. Krein, H. Langer, "Introduction to the spectral theory of operators in spaces with an indefinite metric" , Akademie Verlag (1982) |
Space with an indefinite metric. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Space_with_an_indefinite_metric&oldid=48753