Difference between revisions of "Siegel disc"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | s1101201.png | ||
| + | $#A+1 = 51 n = 1 | ||
| + | $#C+1 = 51 : ~/encyclopedia/old_files/data/S110/S.1100120 Siegel disc | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | Consider a holomorphic [[Vector field|vector field]] with a singularity, i.e. of the form $ {\dot{x} } = Ax + \dots $ | |
| + | with $ x \in \mathbf R ^ {b} $ | ||
| + | or $ x \in \mathbf C $. | ||
| + | The eigenvalues $ \lambda _ {1} \dots \lambda _ {n} $ | ||
| + | are said to be resonant if among the eigenvalues there exists a relation of the form $ \lambda _ {s} = ( m , \lambda ) $, | ||
| + | where $ \lambda = ( \lambda _ {1} \dots \lambda _ {n} ) $, | ||
| + | $ m = ( m _ {1} \dots m _ {n} ) $ | ||
| + | with $ m _ {i} \geq 0 $, | ||
| + | $ \sum m _ {i} = | m | \geq 2 $ | ||
| + | and $ ( m , \lambda ) $ | ||
| + | is the usual inner product. H. Poincaré proved in his dissertation that if the eigenvalues of $ A $ | ||
| + | are non-resonant, then $ {\dot{x} } = Ax + \dots $ | ||
| + | can be reduced to the linear equation $ {\dot{y} } = Ay $ | ||
| + | by a formal change of variable $ x = y + \dots $. | ||
| + | The $ | m | $ | ||
| + | th order term of this change of variable is given in terms of lower-order terms divided by a term of the form $ ( m , \lambda ) - \lambda _ {s} $. | ||
| + | Since, in general, such terms can be either zero (in the resonant case) or arbitrarily close to zero (in which case one says that one has [[Small denominators|small denominators]]), the power series $ x = y + \dots $ | ||
| + | in general does not converge. An example that divergence can occur was already given by L. Euler. The eigenvalue vector $ \lambda $ | ||
| + | belongs to the Poincaré domain if zero is not in the convex hull of the eigenvalues $ \lambda _ {j} \in \mathbf C $; | ||
| + | its complement is called the Siegel domain. When the vector of eigenvalues $ \lambda $ | ||
| + | is in the Poincaré domain, the vector field can be reduced to a polynomial vector field (called the normal form) by a biholomorphic change of variables in a neighbourhood of the singularity. If, in addition, there are no resonances, then one can choose the polynomial normal form to be linear. If $ \lambda $ | ||
| + | is in the Siegel domain, then one says it satisfies a Diophantine condition if there exist $ C > 0 $, | ||
| + | $ \nu > 0 $ | ||
| + | such that $ | {\lambda _ {s} - ( m , \lambda ) } | \geq {C / {| m | ^ \nu } } $ | ||
| + | for all $ m _ {i} \geq 0 $ | ||
| + | with $ \sum m _ {i} = | m | \geq 2 $. | ||
| + | Siegel's theorem states that, in this case, the vector field can be reduced to its linear part by a holomorphic change of coordinates in a neighbourhood of the singularity. Siegel sketched a proof of this result in 1942, but only in the 1970s complete proofs of this theorem were given (by A.N. Kolmogorov, J. Moser, V.I. Arnol'd, M.R. Herman, J.-C. Yoccoz and many others in various settings, e.g. in the $ C ^ {k} $ | ||
| + | category). Many problems concerning invariant tori are based on similar small denominator estimates. | ||
| − | + | In the discrete case, when one considers a mapping $ F ( x ) = Ax + \dots $, | |
| + | the analogous results also holds. In that case, the vector of eigenvalues $ \lambda $ | ||
| + | is in the Poincaré domain if the norm of all the eigenvalues $ \lambda _ {i} $ | ||
| + | are all smaller or all greater than one. The complement is again called the Siegel domain. If the dimension $ n = 1 $, | ||
| + | then this reduces to the unit circle $ | \lambda | = 1 $. | ||
| − | i) the | + | In fact, in one-dimension the Siegel case is completely understood. So, assume that $ | \lambda | = 1 $ |
| + | and that $ \lambda $ | ||
| + | is not a root of unity. Write $ \lambda = { \mathop{\rm exp} } ( 2 \pi i \alpha ) $ | ||
| + | and let $ { {p _ {n} } / {q _ {n} } } $ | ||
| + | be the [[Continued fraction|continued fraction]] expansion of $ \alpha $. | ||
| + | If $ \sup _ {n \geq 0 } { {( { \mathop{\rm log} } q _ {n + 1 } ) } / {q _ {n} } } = \infty $, | ||
| + | then the formal power series of the linearizing coordinates need not converge (Cremer's theorem). Around 1965, A.D. Bryuno proved that if $ \sum { {( { \mathop{\rm log} } q _ {n + 1 } ) } / {q _ {n} } } < \infty $, | ||
| + | then this power series converges. In the late 1980s, Yoccoz proved the converse: if the Bryuno condition is not satisfied, then there exists a holomorphic diffeomorphism with linear part $ z \mapsto \lambda z $ | ||
| + | which is not holomorphically linearizable. In 1994, Yoccoz was awarded the Field Medal for this achievement. | ||
| − | + | If $ f $ | |
| + | is a rational mapping on the [[Riemann sphere|Riemann sphere]], then Siegel domains appear in the Fatou–Sullivan classification theorem. Let $ J ( f ) $ | ||
| + | be the closure of the set of repelling periodic points (cf. also [[Repelling set|Repelling set]]) and let $ F ( f ) $ | ||
| + | be its complement. $ F ( f ) $ | ||
| + | is also the set of points that have a neighbourhood $ U $ | ||
| + | such that $ f ^ {n} \mid _ {U} $ | ||
| + | forms a [[Normal family|normal family]]. Many properties of these sets were already obtained by G. Julia and P. Fatou in the 1920s and 1930s. Using the measurable Riemann mapping theorem (cf. also [[Quasi-conformal mapping|Quasi-conformal mapping]]), D. Sullivan proved in the 1980s that each connected component of $ F ( f ) $ | ||
| + | is eventually mapped onto a periodic component, and that the periodic components can be of four types: | ||
| − | iii) a Siegel domain (when | + | i) the basin of an attracting periodic point (where the eigenvalue $ \lambda $ |
| + | of the linear part satisfies $ | \lambda | < 1 $); | ||
| + | |||
| + | ii) the basin of a parabolic periodic point (when $ \lambda $ | ||
| + | is a root of unity); | ||
| + | |||
| + | iii) a Siegel domain (when $ \lambda $ | ||
| + | has norm one but is not a root of unity, but still the mapping is holomorphically linearizable on some neighbourhood of the fixed point); | ||
iv) a Herman ring (when the component is an annulus on which the mapping is conjugate to a rotation). | iv) a Herman ring (when the component is an annulus on which the mapping is conjugate to a rotation). | ||
Latest revision as of 08:13, 6 June 2020
Consider a holomorphic vector field with a singularity, i.e. of the form $ {\dot{x} } = Ax + \dots $
with $ x \in \mathbf R ^ {b} $
or $ x \in \mathbf C $.
The eigenvalues $ \lambda _ {1} \dots \lambda _ {n} $
are said to be resonant if among the eigenvalues there exists a relation of the form $ \lambda _ {s} = ( m , \lambda ) $,
where $ \lambda = ( \lambda _ {1} \dots \lambda _ {n} ) $,
$ m = ( m _ {1} \dots m _ {n} ) $
with $ m _ {i} \geq 0 $,
$ \sum m _ {i} = | m | \geq 2 $
and $ ( m , \lambda ) $
is the usual inner product. H. Poincaré proved in his dissertation that if the eigenvalues of $ A $
are non-resonant, then $ {\dot{x} } = Ax + \dots $
can be reduced to the linear equation $ {\dot{y} } = Ay $
by a formal change of variable $ x = y + \dots $.
The $ | m | $
th order term of this change of variable is given in terms of lower-order terms divided by a term of the form $ ( m , \lambda ) - \lambda _ {s} $.
Since, in general, such terms can be either zero (in the resonant case) or arbitrarily close to zero (in which case one says that one has small denominators), the power series $ x = y + \dots $
in general does not converge. An example that divergence can occur was already given by L. Euler. The eigenvalue vector $ \lambda $
belongs to the Poincaré domain if zero is not in the convex hull of the eigenvalues $ \lambda _ {j} \in \mathbf C $;
its complement is called the Siegel domain. When the vector of eigenvalues $ \lambda $
is in the Poincaré domain, the vector field can be reduced to a polynomial vector field (called the normal form) by a biholomorphic change of variables in a neighbourhood of the singularity. If, in addition, there are no resonances, then one can choose the polynomial normal form to be linear. If $ \lambda $
is in the Siegel domain, then one says it satisfies a Diophantine condition if there exist $ C > 0 $,
$ \nu > 0 $
such that $ | {\lambda _ {s} - ( m , \lambda ) } | \geq {C / {| m | ^ \nu } } $
for all $ m _ {i} \geq 0 $
with $ \sum m _ {i} = | m | \geq 2 $.
Siegel's theorem states that, in this case, the vector field can be reduced to its linear part by a holomorphic change of coordinates in a neighbourhood of the singularity. Siegel sketched a proof of this result in 1942, but only in the 1970s complete proofs of this theorem were given (by A.N. Kolmogorov, J. Moser, V.I. Arnol'd, M.R. Herman, J.-C. Yoccoz and many others in various settings, e.g. in the $ C ^ {k} $
category). Many problems concerning invariant tori are based on similar small denominator estimates.
In the discrete case, when one considers a mapping $ F ( x ) = Ax + \dots $, the analogous results also holds. In that case, the vector of eigenvalues $ \lambda $ is in the Poincaré domain if the norm of all the eigenvalues $ \lambda _ {i} $ are all smaller or all greater than one. The complement is again called the Siegel domain. If the dimension $ n = 1 $, then this reduces to the unit circle $ | \lambda | = 1 $.
In fact, in one-dimension the Siegel case is completely understood. So, assume that $ | \lambda | = 1 $ and that $ \lambda $ is not a root of unity. Write $ \lambda = { \mathop{\rm exp} } ( 2 \pi i \alpha ) $ and let $ { {p _ {n} } / {q _ {n} } } $ be the continued fraction expansion of $ \alpha $. If $ \sup _ {n \geq 0 } { {( { \mathop{\rm log} } q _ {n + 1 } ) } / {q _ {n} } } = \infty $, then the formal power series of the linearizing coordinates need not converge (Cremer's theorem). Around 1965, A.D. Bryuno proved that if $ \sum { {( { \mathop{\rm log} } q _ {n + 1 } ) } / {q _ {n} } } < \infty $, then this power series converges. In the late 1980s, Yoccoz proved the converse: if the Bryuno condition is not satisfied, then there exists a holomorphic diffeomorphism with linear part $ z \mapsto \lambda z $ which is not holomorphically linearizable. In 1994, Yoccoz was awarded the Field Medal for this achievement.
If $ f $ is a rational mapping on the Riemann sphere, then Siegel domains appear in the Fatou–Sullivan classification theorem. Let $ J ( f ) $ be the closure of the set of repelling periodic points (cf. also Repelling set) and let $ F ( f ) $ be its complement. $ F ( f ) $ is also the set of points that have a neighbourhood $ U $ such that $ f ^ {n} \mid _ {U} $ forms a normal family. Many properties of these sets were already obtained by G. Julia and P. Fatou in the 1920s and 1930s. Using the measurable Riemann mapping theorem (cf. also Quasi-conformal mapping), D. Sullivan proved in the 1980s that each connected component of $ F ( f ) $ is eventually mapped onto a periodic component, and that the periodic components can be of four types:
i) the basin of an attracting periodic point (where the eigenvalue $ \lambda $ of the linear part satisfies $ | \lambda | < 1 $);
ii) the basin of a parabolic periodic point (when $ \lambda $ is a root of unity);
iii) a Siegel domain (when $ \lambda $ has norm one but is not a root of unity, but still the mapping is holomorphically linearizable on some neighbourhood of the fixed point);
iv) a Herman ring (when the component is an annulus on which the mapping is conjugate to a rotation).
References
| [a1] | V.I. Arnol'd, "Geometrical methods in the theory of ordinary differential equations" , Grundlehren math. Wiss. , 250 , Springer (1983) (In Russian) |
| [a2] | A.D. Bryuno, "Analytical form of differential equations" Trans. Moscow Math. Soc. , 25 (1971) pp. 131–288 (In Russian) (Also: 26 (1972), 199–239) |
| [a3] | M.R. Herman, "Recent results and some open questions on Siegel's linearisation theorem of germs of complex analytic diffeomorphisms of 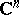 near a fixed point" , Proc. VIII Int. Conf. Math. Phys. , World Sci. (1987) near a fixed point" , Proc. VIII Int. Conf. Math. Phys. , World Sci. (1987) |
| [a4] | C.L. Siegel, "Iteration of analytic functions" Ann. of Math. , 43 (1942) pp. 807–812 |
| [a5] | C.L. Siegel, J. Moser, "Lectures on celestial mechanics" , Springer (1971) |
| [a6] | J.-C. Yoccoz, "Théorème de Siegel, polynômes quadratiques et nombres de Brjuno" Astérisque , 231 (1995) |
Siegel disc. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Siegel_disc&oldid=48692