Difference between revisions of "Semi-group of non-linear operators"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | s0841301.png | ||
| + | $#A+1 = 218 n = 1 | ||
| + | $#C+1 = 218 : ~/encyclopedia/old_files/data/S084/S.0804130 Semi\AAhgroup of non\AAhlinear operators | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A one-parameter family of operators $ S ( t ) $, | |
| + | $ 0 \leq t < \infty $, | ||
| + | defined and acting on a closed subset $ G $ | ||
| + | of a [[Banach space|Banach space]] $ X $, | ||
| + | with the following properties: | ||
| − | + | 1) $ S ( t + \tau ) x = S ( t ) ( S ( \tau ) x ) $ | |
| + | for $ x \in C $, | ||
| + | $ t , \tau > 0 $; | ||
| − | + | 2) $ S ( 0 ) x = x $ | |
| + | for any $ x \in C $; | ||
| − | + | 3) for any $ x \in C $, | |
| + | the function $ S ( t ) x $( | ||
| + | with values in $ X $) | ||
| + | is continuous with respect to $ t $ | ||
| + | on $ [ 0 , \infty ) $. | ||
| − | A semi-group of type | + | A semi-group $ S ( t ) $ |
| + | is of type $ \omega $ | ||
| + | if | ||
| − | + | $$ | |
| + | \| S ( t ) x - S ( t ) y \| \leq e ^ {\omega t } \| x - y \| ,\ \ | ||
| + | x , y \in C ,\ t> 0 . | ||
| + | $$ | ||
| − | + | A semi-group of type $ 0 $ | |
| + | is called a contraction semi-group. | ||
| − | + | As in the case of semi-groups of linear operators (cf. [[Semi-group of operators|Semi-group of operators]]), one introduces the concept of the generating operator (or infinitesimal generator) $ A _ {0} $ | |
| + | of the semi-group $ S ( t ) $: | ||
| − | + | $$ | |
| + | A _ {0} x = \lim\limits _ {h \rightarrow 0 } | ||
| + | \frac{S ( h ) x - x }{h} | ||
| − | + | $$ | |
| − | + | for those elements $ x \in C $ | |
| + | for which the limit exists. If $ S ( t ) $ | ||
| + | is a contraction semi-group, $ A _ {0} $ | ||
| + | is a dissipative operator. Recall that an operator $ A $ | ||
| + | on a Banach space $ X $ | ||
| + | is dissipative if $ \| x - y - \lambda ( Ax - Ay ) \| \geq \| x - y \| $ | ||
| + | for $ x , y \in \overline{ {D ( A) }}\; $, | ||
| + | $ \lambda > 0 $. | ||
| + | A dissipative operator may be multi-valued, in which case $ Ax $ | ||
| + | in the definition stands for any of its values at $ x $. | ||
| + | A dissipative operator is said to be $ m $- | ||
| + | dissipative if $ \mathop{\rm Range} ( I - \lambda A ) = X $ | ||
| + | for $ \lambda > 0 $. | ||
| + | If $ S ( t ) $ | ||
| + | is of type $ \omega $, | ||
| + | then $ A _ {0} - \omega I $ | ||
| + | is dissipative. | ||
| − | + | The fundamental theorem on the generation of semi-groups: If $ A - \omega I $ | |
| + | is a dissipative operator and $ \mathop{\rm Range} ( I - \lambda A ) $ | ||
| + | contains $ D ( A ) $ | ||
| + | for sufficiently small $ \lambda > 0 $, | ||
| + | then there exists a semi-group $ S _ {A} ( t ) $ | ||
| + | of type $ \omega $ | ||
| + | on $ \overline{ {D ( A ) }}\; $ | ||
| + | such that | ||
| − | + | $$ | |
| + | S _ {A} ( t ) x = \lim\limits _ {n \rightarrow \infty } \ | ||
| + | \left ( I - | ||
| + | \frac{t}{n} | ||
| + | A \right ) ^ {-} n x , | ||
| + | $$ | ||
| − | + | where $ x \in \overline{ {D ( A ) }}\; $ | |
| + | and the convergence is uniform on any finite $ t $- | ||
| + | interval. (The existence of $ S _ {A} ( t ) $ | ||
| + | can also be proved if one replaces the condition $ \mathop{\rm Range} ( I - \lambda A ) \supset \overline{ {D ( A ) }}\; $ | ||
| + | by the weaker condition | ||
| − | + | $$ | |
| + | \lim\limits _ {\overline{ {\lambda \downarrow 0 }}\; } \ | ||
| + | \lambda ^ {-} 1 d ( \mathop{\rm Range} ( I - \lambda A ) , x ) = 0 , | ||
| + | $$ | ||
| − | + | where $ d $ | |
| + | is the distance between sets.) | ||
| − | + | For any operator $ A $ | |
| + | one has a corresponding Cauchy problem | ||
| − | + | $$ \tag{* } | |
| − | + | \frac{du}{dt} | |
| + | ( t) \in Au ( t ) ,\ t > 0 ,\ u ( 0) = x . | ||
| + | $$ | ||
| − | + | If the problem (*) has a strong solution, i.e. if there exists a function $ u ( t ) $ | |
| + | which is continuous on $ [ 0 , \infty ) $, | ||
| + | absolutely continuous on any compact subset of $ ( 0, \infty ) $, | ||
| + | takes values in $ D ( A ) $ | ||
| + | for almost all $ t > 0 $, | ||
| + | has a strong derivative for almost all $ t > 0 $, | ||
| + | and satisfies the relation (*), then $ u ( t ) = S _ {A} ( t ) x $. | ||
| + | Any function $ S _ {A} ( t ) x $ | ||
| + | is a unique integral solution of the problem (*). | ||
| − | + | Under the assumptions of the fundamental theorem, if $ X $ | |
| + | is a [[Reflexive space|reflexive space]] and $ A $ | ||
| + | is closed (cf. [[Closed operator|Closed operator]]), then the function $ u ( t ) = S _ {A} ( t ) x $ | ||
| + | yields a strong solution of the Cauchy problem (*) for $ x \in D ( A) $, | ||
| + | with $ ( du / dt) ( t) \in A ^ {0} u ( t ) $ | ||
| + | almost everywhere, where $ A ^ {0} z $ | ||
| + | is the set of elements of minimal norm in $ Az $. | ||
| + | In that case the generating operator $ A _ {0} $ | ||
| + | of the semi-group $ S _ {A} ( t ) $ | ||
| + | is densely defined: $ \overline{ {D ( A _ {0} ) }}\; = \overline{ {D ( A ) }}\; $. | ||
| + | If, moreover, $ X $ | ||
| + | and $ X ^ \prime $ | ||
| + | are uniformly convex, then the operator $ A ^ {0} $ | ||
| + | is single-valued and for all $ t \geq 0 $ | ||
| + | there exists a right derivative $ d ^ {+} u / dt = A ^ {0} u ( t ) $; | ||
| + | this function is continuous from the right on $ [ 0, \infty ) $, | ||
| + | and continuous at all points with the possible exception of a countable set; in this case $ D ( A _ {0} ) = D ( A ) $ | ||
| + | and $ A _ {0} = A ^ {0} $. | ||
| − | + | If $ X $ | |
| + | is reflexive (or $ X = Y ^ \prime $, | ||
| + | where $ Y $ | ||
| + | is separable) and $ A $ | ||
| + | is a single-valued operator and has the property that $ x _ {n} \rightarrow x $ | ||
| + | in $ X $ | ||
| + | and $ Ax _ {n} \rightarrow y $ | ||
| + | in the [[Weak topology|weak topology]] $ \sigma ( X , X ^ \prime ) $( | ||
| + | respectively, in $ \sigma ( X , Y ) $) | ||
| + | imply $ y = Ax $, | ||
| + | then $ u ( t) \in D ( A ) $, | ||
| + | $ t \geq 0 $, | ||
| + | and $ u ( t ) $ | ||
| + | is a weakly (weak- $ * $) | ||
| + | continuously-differentiable solution of the problem (*). In the non-reflexive case, examples are known where the assumptions of the fundamental theorem hold with $ \overline{ {D ( A) }}\; = X $ | ||
| + | and the functions $ u ( t ) = S _ {A} ( t ) x $ | ||
| + | do not even have weak derivatives on $ X $ | ||
| + | at any $ x \in X $, | ||
| + | $ t \geq 0 $. | ||
| − | + | Let $ A $ | |
| + | be a continuous operator, defined on all of $ X $, | ||
| + | such that $ A - \omega I $ | ||
| + | is dissipative. Then $ \mathop{\rm Range} ( I - \lambda A ) = X $ | ||
| + | for $ \lambda > 0 $, | ||
| + | $ \lambda \omega < 1 $, | ||
| + | and for any $ x \in X $ | ||
| + | the problem (*) has a unique continuously-differentiable solution on $ [ 0 , \infty ) $, | ||
| + | given by $ u ( t ) = S _ {A} ( t ) x $. | ||
| + | If $ A $ | ||
| + | is continuous on its closed domain $ D ( A ) $, | ||
| + | then it will be the generating operator of a semi-group of type $ \omega $ | ||
| + | on $ D ( A) $ | ||
| + | if only and only if $ A - \omega I $ | ||
| + | is dissipative and $ \lim\limits _ {\lambda \rightarrow 0 } \lambda ^ {-} 1 d ( x + \lambda Ax , D ( A ) ) = 0 $ | ||
| + | for $ x \in D ( A) $. | ||
| − | + | In a [[Hilbert space|Hilbert space]] $ H $, | |
| + | a contraction semi-group on a set $ C $ | ||
| + | may be extended to a contraction semi-group on a closed convex subset $ \widetilde{C} $ | ||
| + | of $ H $. | ||
| + | Moreover, the generating operator $ A _ {0} $ | ||
| + | of the extended semi-group is defined on a set dense in $ \widetilde{C} $. | ||
| + | There exists a unique $ m $- | ||
| + | dissipative operator such that $ \overline{ {D ( A) }}\; = C $ | ||
| + | and $ A _ {0} = A ^ {0} $. | ||
| + | If $ A $ | ||
| + | is $ m $- | ||
| + | dissipative, then $ \overline{ {D ( A) }}\; $ | ||
| + | is convex and there exists a unique contraction semi-group $ S ( t ) = S _ {A} ( t) $ | ||
| + | on $ \overline{ {D ( A) }}\; $ | ||
| + | such that $ A _ {0} = A ^ {0} $. | ||
| − | + | Let $ \phi $ | |
| + | be a convex semi-continuous functional defined on a real Hilbert space $ H $ | ||
| + | and let $ \partial \phi $ | ||
| + | be its [[Subdifferential|subdifferential]]; then the operator $ Ax = - \partial \phi ( x) $( | ||
| + | for all $ x $ | ||
| + | such that $ \partial \phi ( x) $ | ||
| + | is non-empty) is dissipative. The semi-group $ S _ {A} ( t ) $ | ||
| + | possesses properties similar to those of a linear analytic semi-group. In particular, $ S _ {A} ( t) x \in D ( A) $( | ||
| + | $ t> 0 $) | ||
| + | for any $ x \in \overline{ {D ( A) }}\; $, | ||
| + | and $ u ( t ) = S _ {A} ( t) x $ | ||
| + | is a strong solution of the Cauchy problem (*), with | ||
| − | + | $$ | |
| + | \left \| | ||
| + | \frac{d ^ {+} u }{dt} | ||
| + | ( t) \right \| = \ | ||
| + | \| A ^ {0} u ( t ) \| \leq | ||
| + | \frac{2}{t} | ||
| + | \ | ||
| + | \| x - v \| + 2 \| A ^ {0} v \| | ||
| + | $$ | ||
| − | + | for all $ t > 0 $, | |
| + | $ v \in D ( A) $. | ||
| + | If $ \phi $ | ||
| + | attains its minimum, then $ u ( t ) $ | ||
| + | converges weakly to some minimum point as $ t \rightarrow \infty $. | ||
| + | |||
| + | Theorems about the approximation of semi-groups play an essential role in the approximate solution of Cauchy problems. Let $ X $, | ||
| + | $ X _ {n} $, | ||
| + | $ n = 1 , 2 \dots $ | ||
| + | be Banach spaces; let $ A $, | ||
| + | $ A _ {n} $ | ||
| + | be operators defined and single-valued on $ X $, | ||
| + | $ X _ {n} $, | ||
| + | respectively, satisfying the assumptions of the fundamental theorem for the same type $ \omega $; | ||
| + | let $ p _ {n} : X \rightarrow X _ {n} $ | ||
| + | be linear operators, $ \| p _ {n} \| _ {X \rightarrow X _ {n} } \leq \textrm{ const } $. | ||
| + | Then convergence of the resolvents (cf. [[Resolvent|Resolvent]]) ( $ \lambda > 0 $, | ||
| + | $ \lambda \omega < 1 $) | ||
| + | |||
| + | $$ | ||
| + | \| ( I - \lambda A _ {n} ) ^ {-} 1 p _ {n} x - p _ {n} ( I - \lambda A ) ^ {-} 1 | ||
| + | x \| _ {X _ {n} } \rightarrow 0 | ||
| + | $$ | ||
| + | |||
| + | for $ x \in \overline{ {D ( A) }}\; $ | ||
| + | implies convergence of the semi-groups | ||
| + | |||
| + | $$ | ||
| + | \| S _ {A _ {n} } ( t) p _ {n} x - p _ {n} S _ {A} ( t) x \| _ {X _ {n} } | ||
| + | \rightarrow 0 ,\ x \in \overline{ {D ( A) }}\; , | ||
| + | $$ | ||
uniformly on any finite closed interval. | uniformly on any finite closed interval. | ||
| − | The multiplicative formulas developed by S. Lie in the finite-dimensional linear case can be generalized to the non-linear case. If | + | The multiplicative formulas developed by S. Lie in the finite-dimensional linear case can be generalized to the non-linear case. If $ A $, |
| + | $ B $ | ||
| + | and $ A + B $ | ||
| + | are single-valued $ m $- | ||
| + | dissipative operators on a Hilbert space and the closed convex set $ C \subset \overline{ {D ( A) }}\; \cap \overline{ {D ( B) }}\; $ | ||
| + | is invariant under $ ( I - \lambda A ) ^ {-} 1 $ | ||
| + | and $ ( I - \lambda B ) ^ {-} 1 $, | ||
| + | then, for any $ x \in C \cap \overline{ {D ( A) \cap D ( B) }}\; $, | ||
| − | + | $$ \tag{** } | |
| + | S _ {A + B } ( t) x = \lim\limits _ {n \rightarrow \infty } \ | ||
| + | \left [ S _ {A} \left ( | ||
| − | + | \frac{t}{n} | |
| + | \right ) S _ {B} \left ( | ||
| + | \frac{t}{n} | ||
| + | \right ) \right ] ^ {n} x . | ||
| + | $$ | ||
| − | + | This formula is also valid in an arbitrary Banach space $ X $ | |
| + | for any $ x \in X $, | ||
| + | provided $ A $ | ||
| + | is a densely-defined $ m $- | ||
| + | dissipative linear operator and $ B $ | ||
| + | is a continuous dissipative operator defined on all of $ X $. | ||
| + | In both cases | ||
| − | + | $$ | |
| + | S _ {A + B } ( t) x = \lim\limits \ | ||
| + | \left [ \left ( I - | ||
| + | \frac{t}{n} | ||
| + | B \right ) ^ {-} 1 | ||
| + | \left ( I - | ||
| + | \frac{t}{n} | ||
| + | A \right ) ^ {-} 1 \right ] ^ {n} x , | ||
| + | $$ | ||
| − | Examples of non-linear differential operators satisfying the conditions of the fundamental theorem on the generation of semi-groups are given below. In each case only the space | + | $$ |
| + | x \in \overline{ {D ( A) \cap D ( B) }}\; . | ||
| + | $$ | ||
| + | |||
| + | Examples of non-linear differential operators satisfying the conditions of the fundamental theorem on the generation of semi-groups are given below. In each case only the space $ X $ | ||
| + | and the boundary conditions are indicated, while $ D ( A) $ | ||
| + | is not described. In all examples, $ \Omega $ | ||
| + | is a bounded domain in $ \mathbf R ^ {n} $ | ||
| + | with smooth boundary; $ \beta , \gamma $ | ||
| + | are multi-valued maximal monotone mappings $ \mathbf R \rightarrow \mathbf R $, | ||
| + | $ \beta ( 0) \ni 0 $, | ||
| + | $ \gamma ( 0) \ni 0 $; | ||
| + | and $ \psi : \mathbf R \rightarrow \mathbf R $ | ||
| + | is a continuous strictly-increasing function, $ \psi ( 0) = 0 $. | ||
==Example 1.== | ==Example 1.== | ||
| − | + | $ X = L _ {p} ( \Omega ) $, | |
| + | $ 1 \leq p \leq \infty $, | ||
| + | $ Au = \Delta u - \beta ( u) $, | ||
| + | $ - \partial u / \partial n \in \gamma ( u) $ | ||
| + | on $ \Gamma $. | ||
==Example 2.== | ==Example 2.== | ||
| − | + | $ X = L _ {1} ( \Omega ) $, | |
| + | $ Au = \Delta \psi ( u) $, | ||
| + | $ - \partial u / \partial n \in \gamma ( u) $ | ||
| + | on $ \Gamma $. | ||
==Example 3.== | ==Example 3.== | ||
| − | + | $ X = W _ {2} ^ {-} 1 ( \Omega ) $, | |
| + | $ Au = \Delta \psi ( u) $, | ||
| + | $ u = 0 $ | ||
| + | on $ \Gamma $. | ||
==Example 4.== | ==Example 4.== | ||
| − | + | $ X = C ( \overline \Omega \; ) $ | |
| + | or $ X = L _ \infty ( \Omega ) $, | ||
| + | $ Au = \psi ( \Delta u ) $, | ||
| + | $ u = 0 $ | ||
| + | on $ \Gamma $. | ||
==Example 5.== | ==Example 5.== | ||
| − | + | $ X = L _ {1} ( \mathbf R ^ {n} ) $, | |
| + | $ Au = \mathop{\rm div} f ( u) $, | ||
| + | where $ f \in C ^ {1} ( \mathbf R ) $ | ||
| + | with values in $ \mathbf R ^ {n} $, | ||
| + | $ f ( 0) = 0 $. | ||
==Example 6.== | ==Example 6.== | ||
| − | + | $ X = L _ \infty ( \mathbf R ) $, | |
| + | $ Au = f ( u _ {x} ) $, | ||
| + | where $ f : \mathbf R \rightarrow \mathbf R $ | ||
| + | is continuous. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> V. Barbu, "Nonlinear semigroups and differential equations in Banach spaces" , Ed. Academici (1976) (Translated from Rumanian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H. Brézis, "Opérateurs maximaux monotones et semigroups de contractions dans les espaces de Hilbert" , North-Holland (1973)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> H. Brézis, A. Pazy, "Convergence and approximation of semigroups of nonlinear operators in Banach spaces" ''J. Funct. Anal.'' , '''9''' : 1 (1972) pp. 63–74</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> M.G. Crandall, T.M. Liggett, "Generation of semi-groups of nonlinear transformations on general Banach spaces" ''Amer. J. Math.'' , '''93''' : 2 (1971) pp. 265–298</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> Y. Kobayashi, "Difference approximation of Gauchy problems for quasi-dissipative operators and generation of nonlinear semigroups" ''J. Math. Soc. Japan'' , '''27''' : 4 (1975) pp. 640–665</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> Y. Konishi, "On the uniform convergence of a finite difference scheme for a nonlinear heat equation" ''Proc. Japan. Acad.'' , '''48''' : 2 (1972) pp. 62–66</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> R.H. Martin, "Differential equations on closed subsets of a Banach space" ''Trans. Amer. Math. Soc.'' , '''179''' (1973) pp. 399–414</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> G.F. Webb, "Continuous nonlinear perturbations of linear accretive operators in Banach spaces" ''J. Funct. Anal.'' , '''10''' : 2 (1972) pp. 191–203</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> M.I. [M.I. Khazan] Hazan, "Nonlinear evolution equations in locally convex spaces" ''Soviet Math. Dokl.'' , '''14''' : 5 (1973) pp. 1608–1614 ''Dokl. Akad. Nauk SSSR'' , '''212''' : 6 (1973) pp. 1309–1312</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> M.I. [M.I. Khazan] Hazan, "Differentiability of nonlinear semigroups and the classical solvability of nonlinear boundary value problems for the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084130/s084130217.png" />" ''Soviet Math. Dokl.'' , '''17''' : 3 (1976) pp. 839–843 ''Dokl. Akad. Nauk SSSR'' , '''228''' : 4 (1976) pp. 805–808</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> V. Barbu, "Nonlinear semigroups and differential equations in Banach spaces" , Ed. Academici (1976) (Translated from Rumanian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H. Brézis, "Opérateurs maximaux monotones et semigroups de contractions dans les espaces de Hilbert" , North-Holland (1973)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> H. Brézis, A. Pazy, "Convergence and approximation of semigroups of nonlinear operators in Banach spaces" ''J. Funct. Anal.'' , '''9''' : 1 (1972) pp. 63–74</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> M.G. Crandall, T.M. Liggett, "Generation of semi-groups of nonlinear transformations on general Banach spaces" ''Amer. J. Math.'' , '''93''' : 2 (1971) pp. 265–298</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> Y. Kobayashi, "Difference approximation of Gauchy problems for quasi-dissipative operators and generation of nonlinear semigroups" ''J. Math. Soc. Japan'' , '''27''' : 4 (1975) pp. 640–665</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> Y. Konishi, "On the uniform convergence of a finite difference scheme for a nonlinear heat equation" ''Proc. Japan. Acad.'' , '''48''' : 2 (1972) pp. 62–66</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> R.H. Martin, "Differential equations on closed subsets of a Banach space" ''Trans. Amer. Math. Soc.'' , '''179''' (1973) pp. 399–414</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> G.F. Webb, "Continuous nonlinear perturbations of linear accretive operators in Banach spaces" ''J. Funct. Anal.'' , '''10''' : 2 (1972) pp. 191–203</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> M.I. [M.I. Khazan] Hazan, "Nonlinear evolution equations in locally convex spaces" ''Soviet Math. Dokl.'' , '''14''' : 5 (1973) pp. 1608–1614 ''Dokl. Akad. Nauk SSSR'' , '''212''' : 6 (1973) pp. 1309–1312</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> M.I. [M.I. Khazan] Hazan, "Differentiability of nonlinear semigroups and the classical solvability of nonlinear boundary value problems for the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084130/s084130217.png" />" ''Soviet Math. Dokl.'' , '''17''' : 3 (1976) pp. 839–843 ''Dokl. Akad. Nauk SSSR'' , '''228''' : 4 (1976) pp. 805–808</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| Line 99: | Line 346: | ||
The formula (**) above, especially in the form | The formula (**) above, especially in the form | ||
| − | + | $$ | |
| + | e ^ {it ( A+ B) } = {s - \lim\limits } _ {n \rightarrow \infty } \ | ||
| + | ( e ^ {itA/n } e ^ {itB/n } ) ^ {n} , | ||
| + | $$ | ||
| − | which holds, e.g., when | + | which holds, e.g., when $ A, B $ |
| + | are self-adjoint operators on a separable Hilbert space so that $ A+ B $, | ||
| + | defined on $ D ( A) \cap D ( B) $, | ||
| + | is self-adjoint, is known as the Trotter product formula, [[#References|[a5]]], [[#References|[a4]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> Ph. Clément, H.J.A.M. Heijmans, S. Angenent, C.J. van Duijn, B. de Pagter, "One-parameter semigroups" , ''CWI Monographs'' , '''5''' , North-Holland (1987)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A. Pazy, "Semigroups of linear operators and applications to partial differential equations" , Springer (1983)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> R.H. Martin, "Nonlinear operators and differential equations in Banach spaces" , Wiley (1976)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> B. Simon, "Functional integration and quantum physics" , Acad. Press (1979) pp. 4–6</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> H. Trotter, "On the product of semigroups of operators" ''Proc. Amer. Math. Soc.'' , '''10''' (1959) pp. 545–551</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> Ph. Clément, H.J.A.M. Heijmans, S. Angenent, C.J. van Duijn, B. de Pagter, "One-parameter semigroups" , ''CWI Monographs'' , '''5''' , North-Holland (1987)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A. Pazy, "Semigroups of linear operators and applications to partial differential equations" , Springer (1983)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> R.H. Martin, "Nonlinear operators and differential equations in Banach spaces" , Wiley (1976)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> B. Simon, "Functional integration and quantum physics" , Acad. Press (1979) pp. 4–6</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> H. Trotter, "On the product of semigroups of operators" ''Proc. Amer. Math. Soc.'' , '''10''' (1959) pp. 545–551</TD></TR></table> | ||
Latest revision as of 08:13, 6 June 2020
A one-parameter family of operators $ S ( t ) $,
$ 0 \leq t < \infty $,
defined and acting on a closed subset $ G $
of a Banach space $ X $,
with the following properties:
1) $ S ( t + \tau ) x = S ( t ) ( S ( \tau ) x ) $ for $ x \in C $, $ t , \tau > 0 $;
2) $ S ( 0 ) x = x $ for any $ x \in C $;
3) for any $ x \in C $, the function $ S ( t ) x $( with values in $ X $) is continuous with respect to $ t $ on $ [ 0 , \infty ) $.
A semi-group $ S ( t ) $ is of type $ \omega $ if
$$ \| S ( t ) x - S ( t ) y \| \leq e ^ {\omega t } \| x - y \| ,\ \ x , y \in C ,\ t> 0 . $$
A semi-group of type $ 0 $ is called a contraction semi-group.
As in the case of semi-groups of linear operators (cf. Semi-group of operators), one introduces the concept of the generating operator (or infinitesimal generator) $ A _ {0} $ of the semi-group $ S ( t ) $:
$$ A _ {0} x = \lim\limits _ {h \rightarrow 0 } \frac{S ( h ) x - x }{h} $$
for those elements $ x \in C $ for which the limit exists. If $ S ( t ) $ is a contraction semi-group, $ A _ {0} $ is a dissipative operator. Recall that an operator $ A $ on a Banach space $ X $ is dissipative if $ \| x - y - \lambda ( Ax - Ay ) \| \geq \| x - y \| $ for $ x , y \in \overline{ {D ( A) }}\; $, $ \lambda > 0 $. A dissipative operator may be multi-valued, in which case $ Ax $ in the definition stands for any of its values at $ x $. A dissipative operator is said to be $ m $- dissipative if $ \mathop{\rm Range} ( I - \lambda A ) = X $ for $ \lambda > 0 $. If $ S ( t ) $ is of type $ \omega $, then $ A _ {0} - \omega I $ is dissipative.
The fundamental theorem on the generation of semi-groups: If $ A - \omega I $ is a dissipative operator and $ \mathop{\rm Range} ( I - \lambda A ) $ contains $ D ( A ) $ for sufficiently small $ \lambda > 0 $, then there exists a semi-group $ S _ {A} ( t ) $ of type $ \omega $ on $ \overline{ {D ( A ) }}\; $ such that
$$ S _ {A} ( t ) x = \lim\limits _ {n \rightarrow \infty } \ \left ( I - \frac{t}{n} A \right ) ^ {-} n x , $$
where $ x \in \overline{ {D ( A ) }}\; $ and the convergence is uniform on any finite $ t $- interval. (The existence of $ S _ {A} ( t ) $ can also be proved if one replaces the condition $ \mathop{\rm Range} ( I - \lambda A ) \supset \overline{ {D ( A ) }}\; $ by the weaker condition
$$ \lim\limits _ {\overline{ {\lambda \downarrow 0 }}\; } \ \lambda ^ {-} 1 d ( \mathop{\rm Range} ( I - \lambda A ) , x ) = 0 , $$
where $ d $ is the distance between sets.)
For any operator $ A $ one has a corresponding Cauchy problem
$$ \tag{* } \frac{du}{dt} ( t) \in Au ( t ) ,\ t > 0 ,\ u ( 0) = x . $$
If the problem (*) has a strong solution, i.e. if there exists a function $ u ( t ) $ which is continuous on $ [ 0 , \infty ) $, absolutely continuous on any compact subset of $ ( 0, \infty ) $, takes values in $ D ( A ) $ for almost all $ t > 0 $, has a strong derivative for almost all $ t > 0 $, and satisfies the relation (*), then $ u ( t ) = S _ {A} ( t ) x $. Any function $ S _ {A} ( t ) x $ is a unique integral solution of the problem (*).
Under the assumptions of the fundamental theorem, if $ X $ is a reflexive space and $ A $ is closed (cf. Closed operator), then the function $ u ( t ) = S _ {A} ( t ) x $ yields a strong solution of the Cauchy problem (*) for $ x \in D ( A) $, with $ ( du / dt) ( t) \in A ^ {0} u ( t ) $ almost everywhere, where $ A ^ {0} z $ is the set of elements of minimal norm in $ Az $. In that case the generating operator $ A _ {0} $ of the semi-group $ S _ {A} ( t ) $ is densely defined: $ \overline{ {D ( A _ {0} ) }}\; = \overline{ {D ( A ) }}\; $. If, moreover, $ X $ and $ X ^ \prime $ are uniformly convex, then the operator $ A ^ {0} $ is single-valued and for all $ t \geq 0 $ there exists a right derivative $ d ^ {+} u / dt = A ^ {0} u ( t ) $; this function is continuous from the right on $ [ 0, \infty ) $, and continuous at all points with the possible exception of a countable set; in this case $ D ( A _ {0} ) = D ( A ) $ and $ A _ {0} = A ^ {0} $.
If $ X $ is reflexive (or $ X = Y ^ \prime $, where $ Y $ is separable) and $ A $ is a single-valued operator and has the property that $ x _ {n} \rightarrow x $ in $ X $ and $ Ax _ {n} \rightarrow y $ in the weak topology $ \sigma ( X , X ^ \prime ) $( respectively, in $ \sigma ( X , Y ) $) imply $ y = Ax $, then $ u ( t) \in D ( A ) $, $ t \geq 0 $, and $ u ( t ) $ is a weakly (weak- $ * $) continuously-differentiable solution of the problem (*). In the non-reflexive case, examples are known where the assumptions of the fundamental theorem hold with $ \overline{ {D ( A) }}\; = X $ and the functions $ u ( t ) = S _ {A} ( t ) x $ do not even have weak derivatives on $ X $ at any $ x \in X $, $ t \geq 0 $.
Let $ A $ be a continuous operator, defined on all of $ X $, such that $ A - \omega I $ is dissipative. Then $ \mathop{\rm Range} ( I - \lambda A ) = X $ for $ \lambda > 0 $, $ \lambda \omega < 1 $, and for any $ x \in X $ the problem (*) has a unique continuously-differentiable solution on $ [ 0 , \infty ) $, given by $ u ( t ) = S _ {A} ( t ) x $. If $ A $ is continuous on its closed domain $ D ( A ) $, then it will be the generating operator of a semi-group of type $ \omega $ on $ D ( A) $ if only and only if $ A - \omega I $ is dissipative and $ \lim\limits _ {\lambda \rightarrow 0 } \lambda ^ {-} 1 d ( x + \lambda Ax , D ( A ) ) = 0 $ for $ x \in D ( A) $.
In a Hilbert space $ H $, a contraction semi-group on a set $ C $ may be extended to a contraction semi-group on a closed convex subset $ \widetilde{C} $ of $ H $. Moreover, the generating operator $ A _ {0} $ of the extended semi-group is defined on a set dense in $ \widetilde{C} $. There exists a unique $ m $- dissipative operator such that $ \overline{ {D ( A) }}\; = C $ and $ A _ {0} = A ^ {0} $. If $ A $ is $ m $- dissipative, then $ \overline{ {D ( A) }}\; $ is convex and there exists a unique contraction semi-group $ S ( t ) = S _ {A} ( t) $ on $ \overline{ {D ( A) }}\; $ such that $ A _ {0} = A ^ {0} $.
Let $ \phi $ be a convex semi-continuous functional defined on a real Hilbert space $ H $ and let $ \partial \phi $ be its subdifferential; then the operator $ Ax = - \partial \phi ( x) $( for all $ x $ such that $ \partial \phi ( x) $ is non-empty) is dissipative. The semi-group $ S _ {A} ( t ) $ possesses properties similar to those of a linear analytic semi-group. In particular, $ S _ {A} ( t) x \in D ( A) $( $ t> 0 $) for any $ x \in \overline{ {D ( A) }}\; $, and $ u ( t ) = S _ {A} ( t) x $ is a strong solution of the Cauchy problem (*), with
$$ \left \| \frac{d ^ {+} u }{dt} ( t) \right \| = \ \| A ^ {0} u ( t ) \| \leq \frac{2}{t} \ \| x - v \| + 2 \| A ^ {0} v \| $$
for all $ t > 0 $, $ v \in D ( A) $. If $ \phi $ attains its minimum, then $ u ( t ) $ converges weakly to some minimum point as $ t \rightarrow \infty $.
Theorems about the approximation of semi-groups play an essential role in the approximate solution of Cauchy problems. Let $ X $, $ X _ {n} $, $ n = 1 , 2 \dots $ be Banach spaces; let $ A $, $ A _ {n} $ be operators defined and single-valued on $ X $, $ X _ {n} $, respectively, satisfying the assumptions of the fundamental theorem for the same type $ \omega $; let $ p _ {n} : X \rightarrow X _ {n} $ be linear operators, $ \| p _ {n} \| _ {X \rightarrow X _ {n} } \leq \textrm{ const } $. Then convergence of the resolvents (cf. Resolvent) ( $ \lambda > 0 $, $ \lambda \omega < 1 $)
$$ \| ( I - \lambda A _ {n} ) ^ {-} 1 p _ {n} x - p _ {n} ( I - \lambda A ) ^ {-} 1 x \| _ {X _ {n} } \rightarrow 0 $$
for $ x \in \overline{ {D ( A) }}\; $ implies convergence of the semi-groups
$$ \| S _ {A _ {n} } ( t) p _ {n} x - p _ {n} S _ {A} ( t) x \| _ {X _ {n} } \rightarrow 0 ,\ x \in \overline{ {D ( A) }}\; , $$
uniformly on any finite closed interval.
The multiplicative formulas developed by S. Lie in the finite-dimensional linear case can be generalized to the non-linear case. If $ A $, $ B $ and $ A + B $ are single-valued $ m $- dissipative operators on a Hilbert space and the closed convex set $ C \subset \overline{ {D ( A) }}\; \cap \overline{ {D ( B) }}\; $ is invariant under $ ( I - \lambda A ) ^ {-} 1 $ and $ ( I - \lambda B ) ^ {-} 1 $, then, for any $ x \in C \cap \overline{ {D ( A) \cap D ( B) }}\; $,
$$ \tag{** } S _ {A + B } ( t) x = \lim\limits _ {n \rightarrow \infty } \ \left [ S _ {A} \left ( \frac{t}{n} \right ) S _ {B} \left ( \frac{t}{n} \right ) \right ] ^ {n} x . $$
This formula is also valid in an arbitrary Banach space $ X $ for any $ x \in X $, provided $ A $ is a densely-defined $ m $- dissipative linear operator and $ B $ is a continuous dissipative operator defined on all of $ X $. In both cases
$$ S _ {A + B } ( t) x = \lim\limits \ \left [ \left ( I - \frac{t}{n} B \right ) ^ {-} 1 \left ( I - \frac{t}{n} A \right ) ^ {-} 1 \right ] ^ {n} x , $$
$$ x \in \overline{ {D ( A) \cap D ( B) }}\; . $$
Examples of non-linear differential operators satisfying the conditions of the fundamental theorem on the generation of semi-groups are given below. In each case only the space $ X $ and the boundary conditions are indicated, while $ D ( A) $ is not described. In all examples, $ \Omega $ is a bounded domain in $ \mathbf R ^ {n} $ with smooth boundary; $ \beta , \gamma $ are multi-valued maximal monotone mappings $ \mathbf R \rightarrow \mathbf R $, $ \beta ( 0) \ni 0 $, $ \gamma ( 0) \ni 0 $; and $ \psi : \mathbf R \rightarrow \mathbf R $ is a continuous strictly-increasing function, $ \psi ( 0) = 0 $.
Example 1.
$ X = L _ {p} ( \Omega ) $, $ 1 \leq p \leq \infty $, $ Au = \Delta u - \beta ( u) $, $ - \partial u / \partial n \in \gamma ( u) $ on $ \Gamma $.
Example 2.
$ X = L _ {1} ( \Omega ) $, $ Au = \Delta \psi ( u) $, $ - \partial u / \partial n \in \gamma ( u) $ on $ \Gamma $.
Example 3.
$ X = W _ {2} ^ {-} 1 ( \Omega ) $, $ Au = \Delta \psi ( u) $, $ u = 0 $ on $ \Gamma $.
Example 4.
$ X = C ( \overline \Omega \; ) $ or $ X = L _ \infty ( \Omega ) $, $ Au = \psi ( \Delta u ) $, $ u = 0 $ on $ \Gamma $.
Example 5.
$ X = L _ {1} ( \mathbf R ^ {n} ) $, $ Au = \mathop{\rm div} f ( u) $, where $ f \in C ^ {1} ( \mathbf R ) $ with values in $ \mathbf R ^ {n} $, $ f ( 0) = 0 $.
Example 6.
$ X = L _ \infty ( \mathbf R ) $, $ Au = f ( u _ {x} ) $, where $ f : \mathbf R \rightarrow \mathbf R $ is continuous.
References
| [1] | V. Barbu, "Nonlinear semigroups and differential equations in Banach spaces" , Ed. Academici (1976) (Translated from Rumanian) |
| [2] | H. Brézis, "Opérateurs maximaux monotones et semigroups de contractions dans les espaces de Hilbert" , North-Holland (1973) |
| [3] | H. Brézis, A. Pazy, "Convergence and approximation of semigroups of nonlinear operators in Banach spaces" J. Funct. Anal. , 9 : 1 (1972) pp. 63–74 |
| [4] | M.G. Crandall, T.M. Liggett, "Generation of semi-groups of nonlinear transformations on general Banach spaces" Amer. J. Math. , 93 : 2 (1971) pp. 265–298 |
| [5] | Y. Kobayashi, "Difference approximation of Gauchy problems for quasi-dissipative operators and generation of nonlinear semigroups" J. Math. Soc. Japan , 27 : 4 (1975) pp. 640–665 |
| [6] | Y. Konishi, "On the uniform convergence of a finite difference scheme for a nonlinear heat equation" Proc. Japan. Acad. , 48 : 2 (1972) pp. 62–66 |
| [7] | R.H. Martin, "Differential equations on closed subsets of a Banach space" Trans. Amer. Math. Soc. , 179 (1973) pp. 399–414 |
| [8] | G.F. Webb, "Continuous nonlinear perturbations of linear accretive operators in Banach spaces" J. Funct. Anal. , 10 : 2 (1972) pp. 191–203 |
| [9] | M.I. [M.I. Khazan] Hazan, "Nonlinear evolution equations in locally convex spaces" Soviet Math. Dokl. , 14 : 5 (1973) pp. 1608–1614 Dokl. Akad. Nauk SSSR , 212 : 6 (1973) pp. 1309–1312 |
| [10] | M.I. [M.I. Khazan] Hazan, "Differentiability of nonlinear semigroups and the classical solvability of nonlinear boundary value problems for the equation 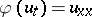 " Soviet Math. Dokl. , 17 : 3 (1976) pp. 839–843 Dokl. Akad. Nauk SSSR , 228 : 4 (1976) pp. 805–808 " Soviet Math. Dokl. , 17 : 3 (1976) pp. 839–843 Dokl. Akad. Nauk SSSR , 228 : 4 (1976) pp. 805–808 |
Comments
See also Semi-group of operators; One-parameter semi-group.
The formula (**) above, especially in the form
$$ e ^ {it ( A+ B) } = {s - \lim\limits } _ {n \rightarrow \infty } \ ( e ^ {itA/n } e ^ {itB/n } ) ^ {n} , $$
which holds, e.g., when $ A, B $ are self-adjoint operators on a separable Hilbert space so that $ A+ B $, defined on $ D ( A) \cap D ( B) $, is self-adjoint, is known as the Trotter product formula, [a5], [a4].
References
| [a1] | Ph. Clément, H.J.A.M. Heijmans, S. Angenent, C.J. van Duijn, B. de Pagter, "One-parameter semigroups" , CWI Monographs , 5 , North-Holland (1987) |
| [a2] | A. Pazy, "Semigroups of linear operators and applications to partial differential equations" , Springer (1983) |
| [a3] | R.H. Martin, "Nonlinear operators and differential equations in Banach spaces" , Wiley (1976) |
| [a4] | B. Simon, "Functional integration and quantum physics" , Acad. Press (1979) pp. 4–6 |
| [a5] | H. Trotter, "On the product of semigroups of operators" Proc. Amer. Math. Soc. , 10 (1959) pp. 545–551 |
Semi-group of non-linear operators. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-group_of_non-linear_operators&oldid=48659