Difference between revisions of "Schur index"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | s0834401.png | ||
| + | $#A+1 = 53 n = 2 | ||
| + | $#C+1 = 53 : ~/encyclopedia/old_files/data/S083/S.0803440 Schur index | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | The Schur index of a central simple algebra $ A $ | |
| + | over a field $ K $( | ||
| + | cf. [[Central simple algebra|Central simple algebra]]) is the degree of the division algebra $ D $ | ||
| + | such that $ A $ | ||
| + | is a full matrix algebra $ M _ {n} ( D) $ | ||
| + | over $ D $. | ||
| − | + | Let $ G $ | |
| + | be a [[Finite group|finite group]], $ K $ | ||
| + | a [[Field|field]] and $ \overline{K}\; $ | ||
| + | the [[Algebraic closure|algebraic closure]] of $ K $. | ||
| + | Let $ V $ | ||
| + | be an irreducible $ \overline{K}\; [ G] $- | ||
| + | module with character $ \rho $( | ||
| + | cf. [[Irreducible module|Irreducible module]]). Let $ K( \rho ) $ | ||
| + | be obtained from $ K $ | ||
| + | by adjoining the values $ \rho ( g) $, | ||
| + | $ g \in G $. | ||
| + | The Schur index of the module $ V $, | ||
| + | $ m _ {K} ( V) $, | ||
| + | (or the Schur index of the character $ \rho $) | ||
| + | is the minimal degree of a field $ S $ | ||
| + | extending $ K( \rho ) $ | ||
| + | such that $ V $ | ||
| + | descends to $ S $, | ||
| + | i.e. such that there is an $ S[ G] $- | ||
| + | module $ W $ | ||
| + | for which $ V \simeq \overline{K}\; \otimes _ {S} W $. | ||
| − | + | For a finite field $ K $ | |
| + | the Schur index is always $ 1 $, | ||
| + | [[#References|[a1]]]. | ||
| − | The | + | A basic result on the Schur index is that for each $ K[ G] $- |
| + | module $ W $ | ||
| + | the multiplicity of $ V $ | ||
| + | in $ \overline{K}\; \otimes _ {K} W $ | ||
| + | is a multiple of $ m _ {K} ( V) $. | ||
| + | |||
| + | A field $ S \subset \overline{K}\; $ | ||
| + | is a splitting field for a finite group $ G $ | ||
| + | if each irreducible $ S[ G] $- | ||
| + | module is absolutely irreducible, i.e. if $ \overline{K}\; \otimes _ {S} V $ | ||
| + | is irreducible. The basic result on the Schur index quoted above readily leads to a proof of R. Brauer's result [[#References|[a1]]] that if $ d $ | ||
| + | is the exponent of a finite group $ G $( | ||
| + | i.e. $ d $ | ||
| + | is the smallest integer such that $ g ^ {d} = e $ | ||
| + | for all $ g \in G $), | ||
| + | then $ \mathbf Q ( 1 ^ {1/d} ) $ | ||
| + | is a splitting field for $ G $. | ||
| + | |||
| + | The set $ S( K) $ | ||
| + | of classes of central simple algebras over $ K $ | ||
| + | which occur as components of a group algebra $ K[ G] $ | ||
| + | for some finite group $ G $ | ||
| + | is a subgroup of the [[Brauer group|Brauer group]] $ \mathop{\rm Br} ( K) $ | ||
| + | of $ K $, | ||
| + | and is known as the Schur subgroup of $ \mathop{\rm Br} ( K) $. | ||
| + | Cf. [[#References|[a4]]] for results on the structure of $ S( K) $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Brauer, "On the representation of a group of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083440/s08344054.png" /> in the field of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083440/s08344055.png" />-th roots of unity" ''Amer. J. Math.'' , '''67''' (1945) pp. 461–471</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962) pp. §90, §41</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> B. Huppert, "Finite groups" , '''2''' , Springer (1982) pp. §1</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> T. Yamada, "The Schur subgroup of the Brauer group" , Springer (1974)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Brauer, "On the representation of a group of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083440/s08344054.png" /> in the field of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083440/s08344055.png" />-th roots of unity" ''Amer. J. Math.'' , '''67''' (1945) pp. 461–471</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962) pp. §90, §41</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> B. Huppert, "Finite groups" , '''2''' , Springer (1982) pp. §1</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> T. Yamada, "The Schur subgroup of the Brauer group" , Springer (1974)</TD></TR></table> | ||
Latest revision as of 08:12, 6 June 2020
The Schur index of a central simple algebra $ A $
over a field $ K $(
cf. Central simple algebra) is the degree of the division algebra $ D $
such that $ A $
is a full matrix algebra $ M _ {n} ( D) $
over $ D $.
Let $ G $ be a finite group, $ K $ a field and $ \overline{K}\; $ the algebraic closure of $ K $. Let $ V $ be an irreducible $ \overline{K}\; [ G] $- module with character $ \rho $( cf. Irreducible module). Let $ K( \rho ) $ be obtained from $ K $ by adjoining the values $ \rho ( g) $, $ g \in G $. The Schur index of the module $ V $, $ m _ {K} ( V) $, (or the Schur index of the character $ \rho $) is the minimal degree of a field $ S $ extending $ K( \rho ) $ such that $ V $ descends to $ S $, i.e. such that there is an $ S[ G] $- module $ W $ for which $ V \simeq \overline{K}\; \otimes _ {S} W $.
For a finite field $ K $ the Schur index is always $ 1 $, [a1].
A basic result on the Schur index is that for each $ K[ G] $- module $ W $ the multiplicity of $ V $ in $ \overline{K}\; \otimes _ {K} W $ is a multiple of $ m _ {K} ( V) $.
A field $ S \subset \overline{K}\; $ is a splitting field for a finite group $ G $ if each irreducible $ S[ G] $- module is absolutely irreducible, i.e. if $ \overline{K}\; \otimes _ {S} V $ is irreducible. The basic result on the Schur index quoted above readily leads to a proof of R. Brauer's result [a1] that if $ d $ is the exponent of a finite group $ G $( i.e. $ d $ is the smallest integer such that $ g ^ {d} = e $ for all $ g \in G $), then $ \mathbf Q ( 1 ^ {1/d} ) $ is a splitting field for $ G $.
The set $ S( K) $ of classes of central simple algebras over $ K $ which occur as components of a group algebra $ K[ G] $ for some finite group $ G $ is a subgroup of the Brauer group $ \mathop{\rm Br} ( K) $ of $ K $, and is known as the Schur subgroup of $ \mathop{\rm Br} ( K) $. Cf. [a4] for results on the structure of $ S( K) $.
References
| [a1] | R. Brauer, "On the representation of a group of order  in the field of 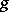 -th roots of unity" Amer. J. Math. , 67 (1945) pp. 461–471 |
| [a2] | C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962) pp. §90, §41 |
| [a3] | B. Huppert, "Finite groups" , 2 , Springer (1982) pp. §1 |
| [a4] | T. Yamada, "The Schur subgroup of the Brauer group" , Springer (1974) |
How to Cite This Entry:
Schur index. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Schur_index&oldid=48623
Schur index. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Schur_index&oldid=48623