Difference between revisions of "Rank of a module"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | r0774701.png | ||
| + | $#A+1 = 29 n = 1 | ||
| + | $#C+1 = 29 : ~/encyclopedia/old_files/data/R077/R.0707470 Rank of a module | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| + | |||
| + | The rank of a left module $ M $ | ||
| + | over a ring $ R $ | ||
| + | imbeddable in a skew-field $ k $ | ||
| + | is the dimension of the tensor product $ k \otimes _ {R} M $, | ||
| + | regarded as a vector space over $ k $. | ||
| + | If $ R = \mathbf Z $, | ||
| + | the ring of integers, the definition coincides with the usual definition of the rank of an Abelian group (cf. [[Rank of a group|Rank of a group]]). If $ k $ | ||
| + | is a flat $ R $- | ||
| + | module (say, $ k $ | ||
| + | is the skew-field of fractions of $ R $, | ||
| + | cf. [[Flat module|Flat module]]), then the ranks of the modules in an exact sequence | ||
| + | |||
| + | $$ | ||
| + | 0 \rightarrow M ^ \prime \rightarrow M \rightarrow M ^ {\prime\prime} \rightarrow 0 | ||
| + | $$ | ||
satisfy the equality | satisfy the equality | ||
| − | + | $$ | |
| + | \mathop{\rm rk} M = \mathop{\rm rk} M ^ \prime + \mathop{\rm rk} M ^ {\prime\prime} . | ||
| + | $$ | ||
| − | The rank of a free module | + | The rank of a free module $ M $ |
| + | over an arbitrary ring $ R $( | ||
| + | cf. [[Free module|Free module]]) is defined as the number of its free generators. For rings that can be imbedded into skew-fields this definition coincides with that in 1). In general, the rank of a free module is not uniquely defined. There are rings (called $ n $- | ||
| + | FI-rings) such that any free module over such a ring with at most $ n $ | ||
| + | free generators has a uniquely-defined rank, while for free modules with more than $ n $ | ||
| + | generators this property does not hold. A sufficient condition for the rank of a free module over a ring $ R $ | ||
| + | to be uniquely defined is the existence of a homomorphism $ \phi : R \rightarrow k $ | ||
| + | into a skew-field $ k $. | ||
| + | In this case the concept of the rank of a module can be extended to projective modules as follows. The homomorphism $ \phi $ | ||
| + | induces a homomorphism of the groups of projective classes $ \phi ^ {*} : K _ {0} R \rightarrow K _ {0} k \approx \mathbf Z $, | ||
| + | and the rank of a projective module $ P $ | ||
| + | is by definition the image of a representative of $ P $ | ||
| + | in $ \mathbf Z $. | ||
| + | Such a homomorphism $ \phi $ | ||
| + | exists for any commutative ring $ R $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> P.M. Cohn, "Free rings and their relations" , Acad. Press (1971)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.W. Milnor, "Introduction to algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077470/r07747029.png" />-theory" , Princeton Univ. Press (1971)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> P.M. Cohn, "Free rings and their relations" , Acad. Press (1971)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.W. Milnor, "Introduction to algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077470/r07747029.png" />-theory" , Princeton Univ. Press (1971)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | The rank of a projective module | + | The rank of a projective module $ P $, |
| + | as defined here, depends on the choice of $ \phi $. | ||
Latest revision as of 08:09, 6 June 2020
The rank of a left module $ M $
over a ring $ R $
imbeddable in a skew-field $ k $
is the dimension of the tensor product $ k \otimes _ {R} M $,
regarded as a vector space over $ k $.
If $ R = \mathbf Z $,
the ring of integers, the definition coincides with the usual definition of the rank of an Abelian group (cf. Rank of a group). If $ k $
is a flat $ R $-
module (say, $ k $
is the skew-field of fractions of $ R $,
cf. Flat module), then the ranks of the modules in an exact sequence
$$ 0 \rightarrow M ^ \prime \rightarrow M \rightarrow M ^ {\prime\prime} \rightarrow 0 $$
satisfy the equality
$$ \mathop{\rm rk} M = \mathop{\rm rk} M ^ \prime + \mathop{\rm rk} M ^ {\prime\prime} . $$
The rank of a free module $ M $ over an arbitrary ring $ R $( cf. Free module) is defined as the number of its free generators. For rings that can be imbedded into skew-fields this definition coincides with that in 1). In general, the rank of a free module is not uniquely defined. There are rings (called $ n $- FI-rings) such that any free module over such a ring with at most $ n $ free generators has a uniquely-defined rank, while for free modules with more than $ n $ generators this property does not hold. A sufficient condition for the rank of a free module over a ring $ R $ to be uniquely defined is the existence of a homomorphism $ \phi : R \rightarrow k $ into a skew-field $ k $. In this case the concept of the rank of a module can be extended to projective modules as follows. The homomorphism $ \phi $ induces a homomorphism of the groups of projective classes $ \phi ^ {*} : K _ {0} R \rightarrow K _ {0} k \approx \mathbf Z $, and the rank of a projective module $ P $ is by definition the image of a representative of $ P $ in $ \mathbf Z $. Such a homomorphism $ \phi $ exists for any commutative ring $ R $.
References
| [1] | P.M. Cohn, "Free rings and their relations" , Acad. Press (1971) |
| [2] | J.W. Milnor, "Introduction to algebraic 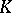 -theory" , Princeton Univ. Press (1971) -theory" , Princeton Univ. Press (1971) |
Comments
The rank of a projective module $ P $, as defined here, depends on the choice of $ \phi $.
Rank of a module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rank_of_a_module&oldid=48433