Difference between revisions of "Projective module"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | p0752801.png | ||
| + | $#A+1 = 76 n = 1 | ||
| + | $#C+1 = 76 : ~/encyclopedia/old_files/data/P075/P.0705280 Projective module | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | Kaplansky's theorem [[#References|[2]]], asserting that every projective module is a direct sum of projective modules with countably many generators, reduces the study of the structure of projective modules to the countable case. Projective modules with finitely many generators are studied in [[Algebraic K-theory|algebraic | + | {{TEX|auto}} |
| + | {{TEX|done}} | ||
| + | |||
| + | A [[Module|module]] $ P $ | ||
| + | satisfying any of the following equivalent conditions: 1) for any [[Epimorphism|epimorphism]] $ \alpha : B \rightarrow C $ | ||
| + | of modules and any homomorphism $ \beta : P \rightarrow C $ | ||
| + | there is a homomorphism $ \gamma : P \rightarrow B $ | ||
| + | such that $ \beta = \alpha \gamma $; | ||
| + | 2) the module $ P $ | ||
| + | is a direct summand of a [[Free module|free module]]; 3) the [[Functor|functor]] $ \mathop{\rm Hom} ( P , - ) $ | ||
| + | is exact (cf. [[Exact functor|Exact functor]]); or 4) any epimorphism $ A \rightarrow P $ | ||
| + | of modules splits. | ||
| + | |||
| + | Kaplansky's theorem [[#References|[2]]], asserting that every projective module is a direct sum of projective modules with countably many generators, reduces the study of the structure of projective modules to the countable case. Projective modules with finitely many generators are studied in [[Algebraic K-theory|algebraic $ K $- | ||
| + | theory]]. The simplest example of a projective module is a free module. Over rings decomposable into a direct sum there always exist projective modules different from free ones. The coincidence of the class of projective modules and that of free modules has been proved for local rings [[#References|[2]]], and for rings of polynomials in several variables over a field (see [[#References|[3]]], [[#References|[4]]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956) {{MR|0077480}} {{ZBL|0075.24305}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J. Kaplansky, "Projective modules" ''Ann. of Math.'' , '''68''' : 2 (1958) pp. 372–377 {{MR|0100017}} {{ZBL|0083.25802}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A.A. Suslin, "Projective modules over a polynomial ring are free" ''Soviet Math. Dokl.'' , '''17''' : 4 (1976) pp. 1160–1164 ''Dokl. Akad. Nauk SSSR'' , '''229''' : 5 (1976) pp. 1063–1066 {{MR|469905}} {{ZBL|0354.13010}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> D. Quillen, "Projective modules over polynomial rings" ''Invent. Math.'' , '''36''' (1976) pp. 167–171 {{MR|0427303}} {{ZBL|0337.13011}} </TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956) {{MR|0077480}} {{ZBL|0075.24305}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J. Kaplansky, "Projective modules" ''Ann. of Math.'' , '''68''' : 2 (1958) pp. 372–377 {{MR|0100017}} {{ZBL|0083.25802}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A.A. Suslin, "Projective modules over a polynomial ring are free" ''Soviet Math. Dokl.'' , '''17''' : 4 (1976) pp. 1160–1164 ''Dokl. Akad. Nauk SSSR'' , '''229''' : 5 (1976) pp. 1063–1066 {{MR|469905}} {{ZBL|0354.13010}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> D. Quillen, "Projective modules over polynomial rings" ''Invent. Math.'' , '''36''' (1976) pp. 167–171 {{MR|0427303}} {{ZBL|0337.13011}} </TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | The theorem that over a ring | + | The theorem that over a ring $ F [ X _ {1} \dots X _ {n} ] $ |
| + | of polynomials in several variables over a field every finitely-generated projective module is free is known as the Quillen–Suslin theorem. The question was raised by J.P. Serre in 1955, [[#References|[a2]]], and the statement is also still known as Serre's conjecture. For a complete and detailed discussion, cf. [[#References|[a3]]]. | ||
| − | In [[#References|[a5]]], the Quillen–Suslin theorem is formulated as: If | + | In [[#References|[a5]]], the Quillen–Suslin theorem is formulated as: If $ M $ |
| + | is a finitely-generated projective $ R [ X ] $- | ||
| + | module and $ f \in R [ X ] $ | ||
| + | is a monic polynomial such that $ M _ {f} $ | ||
| + | is a free $ R [ X ] _ {f} $- | ||
| + | module, then $ M $ | ||
| + | is a free $ R [ X ] $- | ||
| + | module. | ||
| − | Quillen's proof of the Quillen–Suslin theorem uses Horrock's theorem: Let | + | Quillen's proof of the Quillen–Suslin theorem uses Horrock's theorem: Let $ R $ |
| + | be a commutative local ring and $ P $ | ||
| + | a finitely-generated projective module over $ R [ t ] $. | ||
| + | Then if $ R( t) \otimes _ {R [ t ] } P $ | ||
| + | is a free $ R( t) $- | ||
| + | module, $ P $ | ||
| + | is a free $ R[ t] $- | ||
| + | module. A second main ingredient is Quillen's patching theorem. Let $ R $ | ||
| + | be a ring. An $ R [ X _ {1} \dots X _ {n} ] $- | ||
| + | module $ M $ | ||
| + | is extended (from $ R $) | ||
| + | if there exists an $ R $- | ||
| + | module $ M _ {0} $ | ||
| + | such that $ M \simeq R [ X _ {1} \dots X _ {n} ] \otimes _ {R} M _ {0} $. | ||
| + | The patching theorem now says that if $ R $ | ||
| + | is a commutative ring and $ M $ | ||
| + | is a finitely-presented $ R [ X _ {1} \dots X _ {n} ] $- | ||
| + | module, then $ M $ | ||
| + | is extended from $ R $ | ||
| + | if and only if for every maximal ideal $ \mathfrak m $ | ||
| + | of $ R $ | ||
| + | the localization $ M _ {\mathfrak m } $ | ||
| + | is extended from $ R _ {\mathfrak m } $. | ||
| + | In this terminology one has a generalized Quillen–Suslin theorem: If $ k $ | ||
| + | is a commutative regular ring of Krull dimension 2, then every finitely-generated projective module over $ k [ X _ {1} \dots X _ {n} ] $ | ||
| + | is extended from $ k $. | ||
| − | The Murthy–Horrock theorem says that every finitely-generated projective module over | + | The Murthy–Horrock theorem says that every finitely-generated projective module over $ R [ t] $ |
| + | is free if $ R $ | ||
| + | is a commutative regular local ring of Krull dimension 2. | ||
| − | The Suslin monic polynomial theorem played a major role in the study of cancellation theorems over | + | The Suslin monic polynomial theorem played a major role in the study of cancellation theorems over $ k [ X _ {1} \dots X _ {n} ] $. |
| + | (Cancellation theorems are theorems of the type: If $ M \otimes Q \simeq N \oplus Q $, | ||
| + | then $ M \simeq N $. | ||
| + | For instance, there is the Bass cancellation theorem, which says that if $ R $ | ||
| + | is a commutative Noetherian ring of Krull dimension $ d < \infty $ | ||
| + | and $ Q , Q ^ \prime $ | ||
| + | are finitely-generated projective modules which are stably isomorphic, i.e. $ Q \oplus R ^ {s} \simeq Q ^ \prime \oplus R ^ {s} $ | ||
| + | for some $ s $, | ||
| + | and the rank of $ Q $ | ||
| + | is $ > d $, | ||
| + | then $ Q \simeq Q ^ \prime $.) | ||
| + | The monic polynomial theorem says that if $ R $ | ||
| + | is a commutative Noetherian ring of Krull dimension $ d < \infty $ | ||
| + | and $ \mathfrak a $ | ||
| + | is an ideal in $ A = R [ X _ {1} \dots X _ {n} ] $ | ||
| + | of height $ > d $, | ||
| + | then there exist new variables $ Y _ {1} \dots Y _ {n} $ | ||
| + | in $ A $ | ||
| + | such that $ A = R[ Y _ {1} \dots Y _ {n} ] $ | ||
| + | and such that $ \mathfrak a $ | ||
| + | contains a polynomial which is monic as a polynomial in $ Y _ {1} $. | ||
| + | For $ R $ | ||
| + | a field this essentially becomes the Noether normalization theorem. | ||
| − | A commutative ring | + | A commutative ring $ R $ |
| + | is said to be a Hermite ring if every finitely-generated stably free module $ P $( | ||
| + | i.e. $ P \oplus R ^ {s} \simeq R ^ {t} $ | ||
| + | for some $ s, t $) | ||
| + | is free. | ||
| − | Serre's conjecture does not necessarily hold for | + | Serre's conjecture does not necessarily hold for $ D [ X _ {1} \dots X _ {n} ] $ |
| + | if $ n \geq 2 $ | ||
| + | and $ D $ | ||
| + | is a (non-commutation) division ring, [[#References|[a4]]]. The quadratic analogue of Serre's conjecture asks whether a finitely-generated projective module over $ k [ X _ {1} \dots X _ {n} ] $ | ||
| + | equipped with a quadratic, symmetric bilinear, or symplectic form is necessarily extended from a similar object over $ k $. | ||
| + | This is not always the case, cf. [[#References|[a3]]], Chapt. VI, for more details. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H. Bass, "Algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075280/p07528077.png" />-theory" , Benjamin (1968) {{MR|249491}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.-P. Serre, "Faisceaux algébriques cohérents" ''Ann. of Math.'' , '''61''' (1975) pp. 197–278 {{MR|0068874}} {{ZBL|0067.16201}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> T.Y. Lam, "Serre's conjecture" , Springer (1978)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M. Ojanguran, R. Sridharan, "Cancellation of Azumaya algebras" ''J. of Algebra'' , '''18''' (1971) pp. 501–505 {{MR|276271}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> E. Kunz, "Introduction to commutative algebra and algebraic geometry" , Birkhäuser (1985) {{MR|0789602}} {{ZBL|0563.13001}} </TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H. Bass, "Algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075280/p07528077.png" />-theory" , Benjamin (1968) {{MR|249491}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.-P. Serre, "Faisceaux algébriques cohérents" ''Ann. of Math.'' , '''61''' (1975) pp. 197–278 {{MR|0068874}} {{ZBL|0067.16201}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> T.Y. Lam, "Serre's conjecture" , Springer (1978)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M. Ojanguran, R. Sridharan, "Cancellation of Azumaya algebras" ''J. of Algebra'' , '''18''' (1971) pp. 501–505 {{MR|276271}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> E. Kunz, "Introduction to commutative algebra and algebraic geometry" , Birkhäuser (1985) {{MR|0789602}} {{ZBL|0563.13001}} </TD></TR></table> | ||
Latest revision as of 08:08, 6 June 2020
A module $ P $
satisfying any of the following equivalent conditions: 1) for any epimorphism $ \alpha : B \rightarrow C $
of modules and any homomorphism $ \beta : P \rightarrow C $
there is a homomorphism $ \gamma : P \rightarrow B $
such that $ \beta = \alpha \gamma $;
2) the module $ P $
is a direct summand of a free module; 3) the functor $ \mathop{\rm Hom} ( P , - ) $
is exact (cf. Exact functor); or 4) any epimorphism $ A \rightarrow P $
of modules splits.
Kaplansky's theorem [2], asserting that every projective module is a direct sum of projective modules with countably many generators, reduces the study of the structure of projective modules to the countable case. Projective modules with finitely many generators are studied in algebraic $ K $- theory. The simplest example of a projective module is a free module. Over rings decomposable into a direct sum there always exist projective modules different from free ones. The coincidence of the class of projective modules and that of free modules has been proved for local rings [2], and for rings of polynomials in several variables over a field (see [3], [4]).
References
| [1] | H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956) MR0077480 Zbl 0075.24305 |
| [2] | J. Kaplansky, "Projective modules" Ann. of Math. , 68 : 2 (1958) pp. 372–377 MR0100017 Zbl 0083.25802 |
| [3] | A.A. Suslin, "Projective modules over a polynomial ring are free" Soviet Math. Dokl. , 17 : 4 (1976) pp. 1160–1164 Dokl. Akad. Nauk SSSR , 229 : 5 (1976) pp. 1063–1066 MR469905 Zbl 0354.13010 |
| [4] | D. Quillen, "Projective modules over polynomial rings" Invent. Math. , 36 (1976) pp. 167–171 MR0427303 Zbl 0337.13011 |
Comments
The theorem that over a ring $ F [ X _ {1} \dots X _ {n} ] $ of polynomials in several variables over a field every finitely-generated projective module is free is known as the Quillen–Suslin theorem. The question was raised by J.P. Serre in 1955, [a2], and the statement is also still known as Serre's conjecture. For a complete and detailed discussion, cf. [a3].
In [a5], the Quillen–Suslin theorem is formulated as: If $ M $ is a finitely-generated projective $ R [ X ] $- module and $ f \in R [ X ] $ is a monic polynomial such that $ M _ {f} $ is a free $ R [ X ] _ {f} $- module, then $ M $ is a free $ R [ X ] $- module.
Quillen's proof of the Quillen–Suslin theorem uses Horrock's theorem: Let $ R $ be a commutative local ring and $ P $ a finitely-generated projective module over $ R [ t ] $. Then if $ R( t) \otimes _ {R [ t ] } P $ is a free $ R( t) $- module, $ P $ is a free $ R[ t] $- module. A second main ingredient is Quillen's patching theorem. Let $ R $ be a ring. An $ R [ X _ {1} \dots X _ {n} ] $- module $ M $ is extended (from $ R $) if there exists an $ R $- module $ M _ {0} $ such that $ M \simeq R [ X _ {1} \dots X _ {n} ] \otimes _ {R} M _ {0} $. The patching theorem now says that if $ R $ is a commutative ring and $ M $ is a finitely-presented $ R [ X _ {1} \dots X _ {n} ] $- module, then $ M $ is extended from $ R $ if and only if for every maximal ideal $ \mathfrak m $ of $ R $ the localization $ M _ {\mathfrak m } $ is extended from $ R _ {\mathfrak m } $. In this terminology one has a generalized Quillen–Suslin theorem: If $ k $ is a commutative regular ring of Krull dimension 2, then every finitely-generated projective module over $ k [ X _ {1} \dots X _ {n} ] $ is extended from $ k $.
The Murthy–Horrock theorem says that every finitely-generated projective module over $ R [ t] $ is free if $ R $ is a commutative regular local ring of Krull dimension 2.
The Suslin monic polynomial theorem played a major role in the study of cancellation theorems over $ k [ X _ {1} \dots X _ {n} ] $. (Cancellation theorems are theorems of the type: If $ M \otimes Q \simeq N \oplus Q $, then $ M \simeq N $. For instance, there is the Bass cancellation theorem, which says that if $ R $ is a commutative Noetherian ring of Krull dimension $ d < \infty $ and $ Q , Q ^ \prime $ are finitely-generated projective modules which are stably isomorphic, i.e. $ Q \oplus R ^ {s} \simeq Q ^ \prime \oplus R ^ {s} $ for some $ s $, and the rank of $ Q $ is $ > d $, then $ Q \simeq Q ^ \prime $.) The monic polynomial theorem says that if $ R $ is a commutative Noetherian ring of Krull dimension $ d < \infty $ and $ \mathfrak a $ is an ideal in $ A = R [ X _ {1} \dots X _ {n} ] $ of height $ > d $, then there exist new variables $ Y _ {1} \dots Y _ {n} $ in $ A $ such that $ A = R[ Y _ {1} \dots Y _ {n} ] $ and such that $ \mathfrak a $ contains a polynomial which is monic as a polynomial in $ Y _ {1} $. For $ R $ a field this essentially becomes the Noether normalization theorem.
A commutative ring $ R $ is said to be a Hermite ring if every finitely-generated stably free module $ P $( i.e. $ P \oplus R ^ {s} \simeq R ^ {t} $ for some $ s, t $) is free.
Serre's conjecture does not necessarily hold for $ D [ X _ {1} \dots X _ {n} ] $ if $ n \geq 2 $ and $ D $ is a (non-commutation) division ring, [a4]. The quadratic analogue of Serre's conjecture asks whether a finitely-generated projective module over $ k [ X _ {1} \dots X _ {n} ] $ equipped with a quadratic, symmetric bilinear, or symplectic form is necessarily extended from a similar object over $ k $. This is not always the case, cf. [a3], Chapt. VI, for more details.
References
| [a1] | H. Bass, "Algebraic 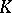 -theory" , Benjamin (1968) MR249491 -theory" , Benjamin (1968) MR249491 |
| [a2] | J.-P. Serre, "Faisceaux algébriques cohérents" Ann. of Math. , 61 (1975) pp. 197–278 MR0068874 Zbl 0067.16201 |
| [a3] | T.Y. Lam, "Serre's conjecture" , Springer (1978) |
| [a4] | M. Ojanguran, R. Sridharan, "Cancellation of Azumaya algebras" J. of Algebra , 18 (1971) pp. 501–505 MR276271 |
| [a5] | E. Kunz, "Introduction to commutative algebra and algebraic geometry" , Birkhäuser (1985) MR0789602 Zbl 0563.13001 |
Projective module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Projective_module&oldid=48322