Difference between revisions of "Profinite group"
m (link) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | A topological group that is the [[Projective limit|projective limit]] of an inverse system of finite discrete groups | + | <!-- |
| + | p0750501.png | ||
| + | $#A+1 = 56 n = 1 | ||
| + | $#C+1 = 56 : ~/encyclopedia/old_files/data/P075/P.0705050 Profinite group | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
| + | A topological group that is the [[Projective limit|projective limit]] of an inverse system of finite discrete groups $ G _ {i} $, | ||
| + | $ i \in I $( | ||
| + | where $ I $ | ||
| + | is a pre-ordered directed set). The profinite group $ G $ | ||
| + | is denoted by $ \lim\limits _ \leftarrow G _ {i} $. | ||
| + | As a subspace of the direct product $ \prod _ {i \in I } G _ {i} $, | ||
| + | endowed with the compact topology (a neighbourhood base of the identity is given by the system of kernels of the projections $ \prod _ {i \in I } G _ {i} \rightarrow G _ {j} $), | ||
| + | it is closed and hence compact. | ||
===Examples.=== | ===Examples.=== | ||
| + | 1) Let $ I $ | ||
| + | be the set of integers larger than zero with the natural order relation, and let $ G _ {i} = \mathbf Z / p ^ {i} \mathbf Z $. | ||
| + | Suppose that $ \tau _ {i} ^ {i+} 1 : G _ {i+} 1 \rightarrow G _ {i} $ | ||
| + | is the natural epimorphism, and put | ||
| − | + | $$ | |
| − | + | \tau _ {i} ^ {j} = \tau _ {i} ^ {i+} 1 \tau _ {i+} 1 ^ {i+} 2 \dots \tau _ {j-} 1 ^ {j} | |
| − | + | $$ | |
| − | for all < | + | for all $ i < j $. |
| + | Then $ \lim\limits _ \leftarrow G _ {i} $ | ||
| + | is the (additive) group of the ring $ \mathbf Z _ {p} $ | ||
| + | of $ p $- | ||
| + | adic integers. | ||
| − | 2) Every compact analytic group over a | + | 2) Every compact analytic group over a $ p $- |
| + | adic number field (e.g. $ \mathop{\rm SL} _ {n} ( \mathbf Z _ {p} ) $) | ||
| + | is profinite as a topological group. | ||
| − | 3) Let | + | 3) Let $ G $ |
| + | be an abstract group and let $ \{ {H _ {i} } : {i \in I } \} $ | ||
| + | be the family of its normal subgroups of finite index. On $ I $ | ||
| + | one introduces the relation $ \leq $, | ||
| + | putting $ i \leq j $ | ||
| + | if $ H _ {i} \supseteq H _ {j} $. | ||
| + | This relation turns $ I $ | ||
| + | into a pre-ordered directed set. Associate to $ i \in I $ | ||
| + | the group $ G / H _ {i} $, | ||
| + | and to each pair $ ( i , j ) $, | ||
| + | $ i \leq j $, | ||
| + | the natural homomorphism $ \tau _ {i} ^ {j} : G / H _ {j} \rightarrow G / H _ {i} $. | ||
| + | One obtains the profinite group $ \widehat{G} = \lim\limits _ \leftarrow G / H _ {i} $, | ||
| + | called the profinite group completion of $ G $. | ||
| + | It is the separable completion of $ G $( | ||
| + | cf. [[Separable completion of a ring|Separable completion of a ring]]) for the topology defined by the subgroups of finite index. The kernel of the natural homomorphism $ G \rightarrow \widehat{G} $ | ||
| + | is the intersection of all subgroups of finite index. In this construction one can consider, instead of the family of all normal subgroups of finite index, only those whose index is a fixed power of a prime number $ p $. | ||
| + | The corresponding group is denoted by $ \widehat{G} _ {p} $, | ||
| + | and is a [[Pro-p group|pro- $ p $- | ||
| + | group]]. | ||
| − | 4) Profinite groups naturally arise in Galois theory of (not necessarily finite) algebraic extensions of fields in the following way. Let | + | 4) Profinite groups naturally arise in Galois theory of (not necessarily finite) algebraic extensions of fields in the following way. Let $ K / k $ |
| + | be a [[Galois extension|Galois extension]] and suppose that $ \{ {K _ {i} / k } : {i \in I } \} $ | ||
| + | is the family of all finite Galois extensions of $ k $ | ||
| + | lying in $ K $. | ||
| + | Then $ K = \cup _ {i \in I } K _ {i} $, | ||
| + | and one can introduce on $ I $ | ||
| + | the relation $ \leq $ | ||
| + | by putting $ i \leq j $ | ||
| + | if $ K _ {i} \subseteq K _ {j} $. | ||
| + | The set $ I $ | ||
| + | then becomes pre-ordered. Let $ \mathop{\rm Gal} ( K _ {i} / k ) $ | ||
| + | be the Galois group of $ K _ {i} / k $. | ||
| + | To every pair $ ( i , j ) \in I \times I $, | ||
| + | $ i \leq j $, | ||
| + | one naturally associates the homomorphism | ||
| − | + | $$ | |
| + | \tau _ {i} ^ {j} : \mathop{\rm Gal} K _ {j} / k \rightarrow \mathop{\rm Gal} K _ {i} / k . | ||
| + | $$ | ||
| − | The corresponding profinite group | + | The corresponding profinite group $ \lim\limits _ \leftarrow \mathop{\rm Gal} ( K _ {i} / k ) $ |
| + | is isomorphic to $ \mathop{\rm Gal} ( K / k ) $, | ||
| + | thus $ \mathop{\rm Gal} ( K / k ) $ | ||
| + | can be considered as a profinite group. The system $ \{ \mathop{\rm Gal} ( K _ {i} / k ) \} _ {i} $ | ||
| + | forms in $ \mathop{\rm Gal} ( K / k ) $ | ||
| + | a neighbourhood base of the identity (cf. [[Galois topological group|Galois topological group]]). This construction has a generalization in algebraic geometry in the definition of the fundamental group of a scheme. | ||
A profinite group can be characterized as a compact totally-disconnected group (cf. [[Compact group|Compact group]]), as well as a compact group that has a system of open normal subgroups forming a [[neighbourhood base]] of the identity. The cohomology theory of profinite groups (cf. [[Cohomology of groups|Cohomology of groups]]; [[Galois cohomology|Galois cohomology]]) plays an important role in modern Galois theory. | A profinite group can be characterized as a compact totally-disconnected group (cf. [[Compact group|Compact group]]), as well as a compact group that has a system of open normal subgroups forming a [[neighbourhood base]] of the identity. The cohomology theory of profinite groups (cf. [[Cohomology of groups|Cohomology of groups]]; [[Galois cohomology|Galois cohomology]]) plays an important role in modern Galois theory. | ||
Revision as of 08:07, 6 June 2020
A topological group that is the projective limit of an inverse system of finite discrete groups $ G _ {i} $,
$ i \in I $(
where $ I $
is a pre-ordered directed set). The profinite group $ G $
is denoted by $ \lim\limits _ \leftarrow G _ {i} $.
As a subspace of the direct product $ \prod _ {i \in I } G _ {i} $,
endowed with the compact topology (a neighbourhood base of the identity is given by the system of kernels of the projections $ \prod _ {i \in I } G _ {i} \rightarrow G _ {j} $),
it is closed and hence compact.
Examples.
1) Let $ I $ be the set of integers larger than zero with the natural order relation, and let $ G _ {i} = \mathbf Z / p ^ {i} \mathbf Z $. Suppose that $ \tau _ {i} ^ {i+} 1 : G _ {i+} 1 \rightarrow G _ {i} $ is the natural epimorphism, and put
$$ \tau _ {i} ^ {j} = \tau _ {i} ^ {i+} 1 \tau _ {i+} 1 ^ {i+} 2 \dots \tau _ {j-} 1 ^ {j} $$
for all $ i < j $. Then $ \lim\limits _ \leftarrow G _ {i} $ is the (additive) group of the ring $ \mathbf Z _ {p} $ of $ p $- adic integers.
2) Every compact analytic group over a $ p $- adic number field (e.g. $ \mathop{\rm SL} _ {n} ( \mathbf Z _ {p} ) $) is profinite as a topological group.
3) Let $ G $ be an abstract group and let $ \{ {H _ {i} } : {i \in I } \} $ be the family of its normal subgroups of finite index. On $ I $ one introduces the relation $ \leq $, putting $ i \leq j $ if $ H _ {i} \supseteq H _ {j} $. This relation turns $ I $ into a pre-ordered directed set. Associate to $ i \in I $ the group $ G / H _ {i} $, and to each pair $ ( i , j ) $, $ i \leq j $, the natural homomorphism $ \tau _ {i} ^ {j} : G / H _ {j} \rightarrow G / H _ {i} $. One obtains the profinite group $ \widehat{G} = \lim\limits _ \leftarrow G / H _ {i} $, called the profinite group completion of $ G $. It is the separable completion of $ G $( cf. Separable completion of a ring) for the topology defined by the subgroups of finite index. The kernel of the natural homomorphism $ G \rightarrow \widehat{G} $ is the intersection of all subgroups of finite index. In this construction one can consider, instead of the family of all normal subgroups of finite index, only those whose index is a fixed power of a prime number $ p $. The corresponding group is denoted by $ \widehat{G} _ {p} $, and is a pro- $ p $- group.
4) Profinite groups naturally arise in Galois theory of (not necessarily finite) algebraic extensions of fields in the following way. Let $ K / k $ be a Galois extension and suppose that $ \{ {K _ {i} / k } : {i \in I } \} $ is the family of all finite Galois extensions of $ k $ lying in $ K $. Then $ K = \cup _ {i \in I } K _ {i} $, and one can introduce on $ I $ the relation $ \leq $ by putting $ i \leq j $ if $ K _ {i} \subseteq K _ {j} $. The set $ I $ then becomes pre-ordered. Let $ \mathop{\rm Gal} ( K _ {i} / k ) $ be the Galois group of $ K _ {i} / k $. To every pair $ ( i , j ) \in I \times I $, $ i \leq j $, one naturally associates the homomorphism
$$ \tau _ {i} ^ {j} : \mathop{\rm Gal} K _ {j} / k \rightarrow \mathop{\rm Gal} K _ {i} / k . $$
The corresponding profinite group $ \lim\limits _ \leftarrow \mathop{\rm Gal} ( K _ {i} / k ) $ is isomorphic to $ \mathop{\rm Gal} ( K / k ) $, thus $ \mathop{\rm Gal} ( K / k ) $ can be considered as a profinite group. The system $ \{ \mathop{\rm Gal} ( K _ {i} / k ) \} _ {i} $ forms in $ \mathop{\rm Gal} ( K / k ) $ a neighbourhood base of the identity (cf. Galois topological group). This construction has a generalization in algebraic geometry in the definition of the fundamental group of a scheme.
A profinite group can be characterized as a compact totally-disconnected group (cf. Compact group), as well as a compact group that has a system of open normal subgroups forming a neighbourhood base of the identity. The cohomology theory of profinite groups (cf. Cohomology of groups; Galois cohomology) plays an important role in modern Galois theory.
References
| [1] | J.-P. Serre, "Cohomologie Galoisienne" , Springer (1964) MR0180551 Zbl 0128.26303 |
| [2] | H. Koch, "Galoissche Theorie der 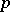 -Erweiterungen" , Deutsch. Verlag Wissenschaft. (1970) -Erweiterungen" , Deutsch. Verlag Wissenschaft. (1970) |
| [3] | J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1986) MR0911121 Zbl 0645.12001 Zbl 0153.07403 |
Profinite group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Profinite_group&oldid=48307