Difference between revisions of "Plus-construction"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | p1101401.png | ||
| + | $#A+1 = 33 n = 10 | ||
| + | $#C+1 = 33 : ~/encyclopedia/old_files/data/P110/P.1100140 Plus\AAhconstruction, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''Quillen plus-construction'' | ''Quillen plus-construction'' | ||
| − | A mapping | + | A mapping $ {q _ {N} } : X \rightarrow {X _ {N} ^ {+} } $ |
| + | between spaces of the [[Homotopy type|homotopy type]] of connected CW-complexes (cf. also [[CW-complex|CW-complex]]), which has $ { \mathop{\rm Ker} } \pi _ {1} ( q _ {N} ) = N $( | ||
| + | necessarily a perfect [[Normal subgroup|normal subgroup]] of $ \pi _ {1} ( X ) $) | ||
| + | and is an acyclic mapping. This means that $ q _ {N} $ | ||
| + | satisfies the following, equivalent, conditions: | ||
| − | the homotopy fibre | + | the homotopy fibre $ {\mathcal A} _ {N} X $ |
| + | of $ q _ {N} $ | ||
| + | is acyclic; | ||
| − | + | $ q _ {N} $ | |
| + | induces an isomorphism of integral [[Homology|homology]] and a trivial action of $ \pi _ {1} ( X _ {N} ^ {+} ) $ | ||
| + | on $ H _ {*} ( {\mathcal A} _ {N} X; \mathbf Z ) $; | ||
| − | + | $ q _ {N} $ | |
| + | induces an isomorphism of homology with any local coefficient system of Abelian groups; | ||
| − | if | + | if $ f : X \rightarrow Y $ |
| + | has $ N \leq { \mathop{\rm Ker} } \pi _ {1} ( f ) $, | ||
| + | then there is a mapping $ g : {X _ {N} ^ {+} } \rightarrow Y $, | ||
| + | unique up to homotopy, such that $ f \simeq g \circ q _ {N} $. | ||
| − | When | + | When $ N $ |
| + | is always chosen to be the maximum perfect subgroup $ {\mathcal P} \pi _ {1} ( X ) $ | ||
| + | of the [[Fundamental group|fundamental group]] of the domain, and the mapping is taken to be a [[Cofibration|cofibration]] (in fact, it can be taken to be an inclusion in a space formed by the adjunction of 2- and 3-cells), this determines a [[Functor|functor]] $ q : X \rightarrow {X ^ {+} } $. | ||
| + | General references are [[#References|[a6]]], [[#References|[a1]]]. A fibre sequence $ F \rightarrow E \rightarrow B $ | ||
| + | induces a fibre sequence $ F ^ {+} \rightarrow E ^ {+} \rightarrow B ^ {+} $ | ||
| + | if and only if $ {\mathcal P} \pi _ {1} ( B ) $ | ||
| + | acts on $ F ^ {+} $ | ||
| + | by mappings freely homotopic to the identity; when the space $ F ^ {+} $ | ||
| + | is nilpotent, this condition reduces to $ {\mathcal P} \pi _ {1} ( B ) $ | ||
| + | acting trivially on $ H _ {*} ( F; \mathbf Z ) $[[#References|[a2]]]. | ||
| − | The construction, first used in [[#References|[a10]]], was developed by D. Quillen [[#References|[a15]]] in order to define the higher [[Algebraic K-theory|algebraic | + | The construction, first used in [[#References|[a10]]], was developed by D. Quillen [[#References|[a15]]] in order to define the higher [[Algebraic K-theory|algebraic $ K $- |
| + | theory]] of a ring $ R $ | ||
| + | as $ K _ {i} ( R ) = \pi _ {i} ( B { \mathop{\rm GL} } ( R ^ {+} ) ) $, | ||
| + | where the infinite general linear group $ { \mathop{\rm GL} } ( R ) $ | ||
| + | is the direct limit of the finite-dimensional groups $ { \mathop{\rm GL} } _ {n} ( R ) $, | ||
| + | and the plus-construction is applied to its classifying space $ B { \mathop{\rm GL} } ( R ) $ | ||
| + | to obtain an infinite [[Loop space|loop space]] (hence spectrum) [[#References|[a16]]]. General references are [[#References|[a12]]], [[#References|[a1]]]. Reconciliation with other approaches to higher $ K $- | ||
| + | theory is found in [[#References|[a5]]], [[#References|[a13]]]. Subsequently, similar procedures have been employed for $ C ^ {*} $- | ||
| + | algebras [[#References|[a8]]] and $ A _ \infty $ | ||
| + | ring spaces [[#References|[a4]]]. | ||
Every connected space can be obtained by the plus-construction on the [[Classifying space|classifying space]] of a discrete group [[#References|[a9]]]. Thus, the construction has also been studied for its effect on the classifying spaces of other groups, for example in connection with knot theory [[#References|[a14]]] and finite group theory [[#References|[a11]]]. Relations with [[Surgery|surgery]] theory can be found in [[#References|[a7]]]. For links to localization theory in [[Algebraic topology|algebraic topology]], see [[#References|[a3]]]. | Every connected space can be obtained by the plus-construction on the [[Classifying space|classifying space]] of a discrete group [[#References|[a9]]]. Thus, the construction has also been studied for its effect on the classifying spaces of other groups, for example in connection with knot theory [[#References|[a14]]] and finite group theory [[#References|[a11]]]. Relations with [[Surgery|surgery]] theory can be found in [[#References|[a7]]]. For links to localization theory in [[Algebraic topology|algebraic topology]], see [[#References|[a3]]]. | ||
Revision as of 08:06, 6 June 2020
Quillen plus-construction
A mapping $ {q _ {N} } : X \rightarrow {X _ {N} ^ {+} } $ between spaces of the homotopy type of connected CW-complexes (cf. also CW-complex), which has $ { \mathop{\rm Ker} } \pi _ {1} ( q _ {N} ) = N $( necessarily a perfect normal subgroup of $ \pi _ {1} ( X ) $) and is an acyclic mapping. This means that $ q _ {N} $ satisfies the following, equivalent, conditions:
the homotopy fibre $ {\mathcal A} _ {N} X $ of $ q _ {N} $ is acyclic;
$ q _ {N} $ induces an isomorphism of integral homology and a trivial action of $ \pi _ {1} ( X _ {N} ^ {+} ) $ on $ H _ {*} ( {\mathcal A} _ {N} X; \mathbf Z ) $;
$ q _ {N} $ induces an isomorphism of homology with any local coefficient system of Abelian groups;
if $ f : X \rightarrow Y $ has $ N \leq { \mathop{\rm Ker} } \pi _ {1} ( f ) $, then there is a mapping $ g : {X _ {N} ^ {+} } \rightarrow Y $, unique up to homotopy, such that $ f \simeq g \circ q _ {N} $.
When $ N $ is always chosen to be the maximum perfect subgroup $ {\mathcal P} \pi _ {1} ( X ) $ of the fundamental group of the domain, and the mapping is taken to be a cofibration (in fact, it can be taken to be an inclusion in a space formed by the adjunction of 2- and 3-cells), this determines a functor $ q : X \rightarrow {X ^ {+} } $. General references are [a6], [a1]. A fibre sequence $ F \rightarrow E \rightarrow B $ induces a fibre sequence $ F ^ {+} \rightarrow E ^ {+} \rightarrow B ^ {+} $ if and only if $ {\mathcal P} \pi _ {1} ( B ) $ acts on $ F ^ {+} $ by mappings freely homotopic to the identity; when the space $ F ^ {+} $ is nilpotent, this condition reduces to $ {\mathcal P} \pi _ {1} ( B ) $ acting trivially on $ H _ {*} ( F; \mathbf Z ) $[a2].
The construction, first used in [a10], was developed by D. Quillen [a15] in order to define the higher algebraic $ K $- theory of a ring $ R $ as $ K _ {i} ( R ) = \pi _ {i} ( B { \mathop{\rm GL} } ( R ^ {+} ) ) $, where the infinite general linear group $ { \mathop{\rm GL} } ( R ) $ is the direct limit of the finite-dimensional groups $ { \mathop{\rm GL} } _ {n} ( R ) $, and the plus-construction is applied to its classifying space $ B { \mathop{\rm GL} } ( R ) $ to obtain an infinite loop space (hence spectrum) [a16]. General references are [a12], [a1]. Reconciliation with other approaches to higher $ K $- theory is found in [a5], [a13]. Subsequently, similar procedures have been employed for $ C ^ {*} $- algebras [a8] and $ A _ \infty $ ring spaces [a4].
Every connected space can be obtained by the plus-construction on the classifying space of a discrete group [a9]. Thus, the construction has also been studied for its effect on the classifying spaces of other groups, for example in connection with knot theory [a14] and finite group theory [a11]. Relations with surgery theory can be found in [a7]. For links to localization theory in algebraic topology, see [a3].
References
| [a1] | A.J. Berrick, "An approach to algebraic 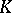 -theory" , Pitman (1982) MR649409 -theory" , Pitman (1982) MR649409 |
| [a2] | A.J. Berrick, "Characterization of plus-constructive fibrations" Adv. in Math. , 48 (1983) pp. 172–176 |
| [a3] | E. Dror Farjoun, "Cellular spaces, null spaces and homotopy localization" , Lecture Notes , 1622 , Springer (1996) MR1392221 Zbl 0842.55001 |
| [a4] | Z. Fiedorowicz, R. Schwänzl, R. Steiner, R.M. Vogt, "Non-connective delooping of 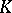 -theory of an -theory of an 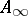 ring space" Math. Z. , 203 (1990) pp. 43–57 MR1030707 ring space" Math. Z. , 203 (1990) pp. 43–57 MR1030707 |
| [a5] | D.R. Grayson, "Higher algebraic 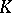 -theory. II (after Daniel Quillen)" , Algebraic -theory. II (after Daniel Quillen)" , Algebraic  -theory (Proc. Conf. Northwestern Univ., Evanston, Ill., 1976) , Lecture Notes in Mathematics , 551 , Springer (1976) pp. 217–240 MR0574096 -theory (Proc. Conf. Northwestern Univ., Evanston, Ill., 1976) , Lecture Notes in Mathematics , 551 , Springer (1976) pp. 217–240 MR0574096 |
| [a6] | J.-C. Hausmann, D. Husemoller, "Acyclic maps" L'Enseign. Math. , 25 (1979) pp. 53–75 MR0543552 Zbl 0412.55008 |
| [a7] | J.-C. Hausmann, P. Vogel, "The plus-construction and lifting maps from manifolds" , Proc. Symp. Pure Math. , 32 , Amer. Math. Soc. (1978) pp. 67–76 MR0520494 Zbl 0409.57036 |
| [a8] | N. Higson, "Algebraic 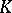 -theory of stable -theory of stable 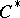 -algebras" Adv. in Math. , 67 (1988) pp. 1–140 MR922140 -algebras" Adv. in Math. , 67 (1988) pp. 1–140 MR922140 |
| [a9] | D.M. Kan, W.P. Thurston, "Every connected space has the homology of a 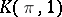 " Topology , 15 (1976) pp. 253–258 MR0413089 Zbl 0355.55004 " Topology , 15 (1976) pp. 253–258 MR0413089 Zbl 0355.55004 |
| [a10] | M. Kervaire, "Smooth homology spheres and their fundamental groups" Trans. Amer. Math. Soc. , 144 (1969) pp. 67–72 MR0253347 Zbl 0187.20401 |
| [a11] | R. Levi, "On finite groups and homotopy theory" , Memoirs , 118 , Amer. Math. Soc. (1995) MR1308466 Zbl 0861.55002 |
| [a12] | J.-L. Loday, "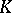 -théorie algébrique et représentations de groupes" Ann. Sci. École Norm. Sup. , 9 (1976) pp. 309–377 MR0447373 Zbl 0362.18014 -théorie algébrique et représentations de groupes" Ann. Sci. École Norm. Sup. , 9 (1976) pp. 309–377 MR0447373 Zbl 0362.18014 |
| [a13] | D. McDuff, G.B. Segal, "Homotopy fibrations and the "group completion" theorem" Invent. Math. , 31 (1976) pp. 279–284 |
| [a14] | W. Meier, "Acyclic maps and knot complements" Math. Ann. , 243 (1979) pp. 247–259 MR0548805 Zbl 0401.57034 |
| [a15] | D. Quillen, "Cohomology of groups" , Actes Congrès Internat. Math. , 2 , Gauthier-Villars (1973) pp. 47–51 MR0488054 MR0488055 Zbl 0249.18022 Zbl 0245.18010 Zbl 0225.55015 Zbl 0225.18011 |
| [a16] | J.B. Wagoner, "Developping classifying spaces in algebraic 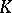 -theory" Topology , 11 (1972) pp. 349–370 -theory" Topology , 11 (1972) pp. 349–370 |
Plus-construction. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Plus-construction&oldid=48193