Difference between revisions of "Parallel straight lines"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | p0713801.png | ||
| + | $#A+1 = 19 n = 0 | ||
| + | $#C+1 = 19 : ~/encyclopedia/old_files/data/P071/P.0701380 Parallel straight lines | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''in Euclidean geometry'' | ''in Euclidean geometry'' | ||
| − | Lines that lie in one plane and that do not intersect. In [[Absolute geometry|absolute geometry]] there passes through a point not lying on a given line at least one line that does not intersect the given one. In [[Euclidean geometry|Euclidean geometry]] there is only one such line. This fact is equivalent to Euclid's [[Fifth postulate|fifth postulate]] (on parallels). In [[Lobachevskii geometry|Lobachevskii geometry]] in the plane there pass through a point | + | Lines that lie in one plane and that do not intersect. In [[Absolute geometry|absolute geometry]] there passes through a point not lying on a given line at least one line that does not intersect the given one. In [[Euclidean geometry|Euclidean geometry]] there is only one such line. This fact is equivalent to Euclid's [[Fifth postulate|fifth postulate]] (on parallels). In [[Lobachevskii geometry|Lobachevskii geometry]] in the plane there pass through a point $ C $( |
| + | see Fig.) outside a given line $ AB $ | ||
| + | infinitely-many lines that do not intersect $ AB $. | ||
| + | Of these only two are called parallel to $ AB $. | ||
| + | A line $ CE $ | ||
| + | is said to be parallel to $ AB $ | ||
| + | in the direction from $ A $ | ||
| + | to $ B $ | ||
| + | if: 1) $ B $ | ||
| + | and $ E $ | ||
| + | lie on the same side of $ AC $; | ||
| + | 2) $ CE $ | ||
| + | does not intersect $ AB $; | ||
| + | and 3) every ray within the angle $ ACE $ | ||
| + | intersects the line $ AB $. | ||
| + | The line $ CF $ | ||
| + | parallel to $ AB $ | ||
| + | in the direction from $ B $ | ||
| + | to $ A $ | ||
| + | is defined similarly. | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/p071380a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/p071380a.gif" /> | ||
Figure: p071380a | Figure: p071380a | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H.S.M. Coxeter, "Parallel lines" ''Canad. Math. Bulletin'' , '''21''' : 4 (1978) pp. 385–397</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Greenberg, "Euclidean and non-Euclidean geometries" , Freeman (1974)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> D. Hilbert, "Grundlagen der Geometrie" , Teubner, reprint (1968)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H.S.M. Coxeter, "Parallel lines" ''Canad. Math. Bulletin'' , '''21''' : 4 (1978) pp. 385–397</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Greenberg, "Euclidean and non-Euclidean geometries" , Freeman (1974)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> D. Hilbert, "Grundlagen der Geometrie" , Teubner, reprint (1968)</TD></TR></table> | ||
Latest revision as of 08:05, 6 June 2020
in Euclidean geometry
Lines that lie in one plane and that do not intersect. In absolute geometry there passes through a point not lying on a given line at least one line that does not intersect the given one. In Euclidean geometry there is only one such line. This fact is equivalent to Euclid's fifth postulate (on parallels). In Lobachevskii geometry in the plane there pass through a point $ C $( see Fig.) outside a given line $ AB $ infinitely-many lines that do not intersect $ AB $. Of these only two are called parallel to $ AB $. A line $ CE $ is said to be parallel to $ AB $ in the direction from $ A $ to $ B $ if: 1) $ B $ and $ E $ lie on the same side of $ AC $; 2) $ CE $ does not intersect $ AB $; and 3) every ray within the angle $ ACE $ intersects the line $ AB $. The line $ CF $ parallel to $ AB $ in the direction from $ B $ to $ A $ is defined similarly.
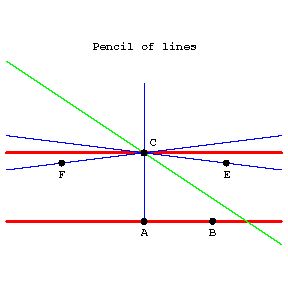
Figure: p071380a
Comments
References
| [a1] | H.S.M. Coxeter, "Parallel lines" Canad. Math. Bulletin , 21 : 4 (1978) pp. 385–397 |
| [a2] | M. Greenberg, "Euclidean and non-Euclidean geometries" , Freeman (1974) |
| [a3] | D. Hilbert, "Grundlagen der Geometrie" , Teubner, reprint (1968) |
How to Cite This Entry:
Parallel straight lines. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Parallel_straight_lines&oldid=48117
Parallel straight lines. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Parallel_straight_lines&oldid=48117
This article was adapted from an original article by BSE-3 (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article