Difference between revisions of "Parallel field"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
|||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | p0713501.png | ||
| + | $#A+1 = 76 n = 1 | ||
| + | $#C+1 = 76 : ~/encyclopedia/old_files/data/P071/P.0701350 Parallel field, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''covariantly-constant field'' | ''covariantly-constant field'' | ||
| − | A tensor field | + | A tensor field $ A $( |
| + | cf. [[Tensor analysis|Tensor analysis]]) on a [[Manifold|manifold]] $ M $ | ||
| + | with a [[Linear connection|linear connection]] $ \nabla $ | ||
| + | that is invariant under [[Parallel displacement(2)|parallel displacement]] along curves on $ M $. | ||
| + | This means that for any points $ p, q \in M $ | ||
| + | the tensor $ A _ {p} $( | ||
| + | the value of the tensor field $ A $ | ||
| + | at the point $ p $) | ||
| + | under the parallel displacement to $ q $ | ||
| + | along any smooth curve joining $ p $ | ||
| + | and $ q $ | ||
| + | transforms to the tensor $ A _ {q} $. | ||
| − | A tensor field | + | A tensor field $ A $ |
| + | is parallel if and only if its [[Covariant derivative|covariant derivative]] in the direction of any vector field $ X $ | ||
| + | vanishes identically: $ \nabla _ {X} A = 0 $ | ||
| + | or, in other words, if the [[Covariant differential|covariant differential]] $ DA $ | ||
| + | of $ A $ | ||
| + | vanishes. | ||
| − | The set | + | The set $ \Pi ( M, \nabla ) $ |
| + | of parallel fields forms a subalgebra of the algebra of all tensor fields on $ M $ | ||
| + | that is invariant under contraction of tensor fields and permutation of their indices. The algebra $ \Pi ( M, \nabla ) $ | ||
| + | is naturally isomorphic to the algebra of tensors at a fixed point $ p $ | ||
| + | of $ M $ | ||
| + | that are invariant under the homogeneous [[Holonomy group|holonomy group]] $ M _ {p} $ | ||
| + | of $ \nabla $ | ||
| + | at $ p $. | ||
| + | For a connection with full holonomy group $ \Gamma = \mathop{\rm GL} ( n, \mathbf R ) $, | ||
| + | where $ n = \mathop{\rm dim} M $, | ||
| + | the algebra $ \Pi ( M, \nabla ) $ | ||
| + | is generated by the Kronecker symbol $ \delta _ {j} ^ {i} $; | ||
| + | for a [[Riemannian connection|Riemannian connection]] with holonomy group $ \textrm{ O } ( n) $— | ||
| + | by the metric tensor $ g = ( g _ {ij} ) $ | ||
| + | and its inverse $ g ^ {-} 1 = ( g ^ {ij} ) $, | ||
| + | and for a Riemannian connection with holonomy group $ \mathop{\rm SO} ( n) $— | ||
| + | by the tensors $ g $ | ||
| + | and $ g ^ {-} 1 $ | ||
| + | and the volume $ n $- | ||
| + | form. There are also descriptions of the generators of the algebra of parallel differential forms on an arbitrary space with a torsion-free linear connection with an arbitrary irreducible holonomy group [[#References|[5]]]. | ||
| − | Of special interest are the parallel fields of differential forms on a Riemannian manifold with a [[Levi-Civita connection|Levi-Civita connection]]. With every such form | + | Of special interest are the parallel fields of differential forms on a Riemannian manifold with a [[Levi-Civita connection|Levi-Civita connection]]. With every such form $ \omega $ |
| + | there is associated (by means of the tensor product with respect to $ \omega $ | ||
| + | and contractions) a number of linear operators in the space of differential forms that commute with the Laplace–Beltrami operator $ \Delta $, | ||
| + | for example, the operator of interior and exterior multiplication by $ \omega $ | ||
| + | or the operator of orthogonal projection onto subspaces of the space of differential forms that are invariant relative to the holonomy group. The study of these operators makes it possible to obtain estimates for the dimensions of the spaces of harmonic forms of various degrees, that is, (in the compact case) for the Betti numbers of $ M $( | ||
| + | see [[#References|[4]]]). The most substantial theory (see [[Hodge theorem|Hodge theorem]]) has been developed for Kähler and for quaternion Kähler manifolds (cf. [[Kähler manifold|Kähler manifold]]), in which there always is a parallel field of $ 2 $- | ||
| + | forms, respectively, of $ 4 $- | ||
| + | forms. Any parallel differential form in a Riemannian space is harmonic. In a compact symmetric Riemannian space the converse is true: Any [[Harmonic form|harmonic form]] is parallel. Therefore, the real cohomology ring of a compact symmetric space is isomorphic to the ring of parallel differential forms. | ||
| − | A tensor field | + | A tensor field $ A $ |
| + | is a parallel field, relative to some linear connection $ \nabla $, | ||
| + | if and only if it is infinitesimally homogeneous, that is, if at every point $ p $ | ||
| + | of $ M $ | ||
| + | there is a frame relative to which the tensor $ A _ {p} $ | ||
| + | has fixed components $ A _ {j _ {1} \dots j _ {l} } ^ {i _ {1} \dots i _ {k} } $ | ||
| + | independent of $ p $. | ||
| + | In this case the set of frames relative to which the tensors $ A _ {p} $, | ||
| + | $ p \in M $, | ||
| + | have the components $ A _ {j _ {1} \dots j _ {l} } ^ {i _ {1} \dots i _ {k} } $ | ||
| + | form a [[G-structure| $ G $- | ||
| + | structure]], that is, the principal subbundle $ P( A) $ | ||
| + | of the bundle of frames with the structure group $ G $, | ||
| + | where $ G $ | ||
| + | is the stabilizer of $ A _ {p} $ | ||
| + | under the action of the group $ \mathop{\rm GL} ( n, \mathbf R ) $ | ||
| + | on the tensor space. The field $ A $ | ||
| + | is parallel relative to any connection in the $ G $- | ||
| + | structure $ P( A) $. | ||
| + | In particular, any section of $ P( A) $( | ||
| + | if it exists) gives a connection with zero curvature relative to which $ A $ | ||
| + | is a parallel field. | ||
| − | More complicated is the problem of the existence of torsion-free connections relative to which a given infinitesimally-homogeneous field is parallel. If | + | More complicated is the problem of the existence of torsion-free connections relative to which a given infinitesimally-homogeneous field is parallel. If $ A $ |
| + | has a pseudo-Riemannian metric, then such a connection (a Levi-Civita connection) always exists, and is unique. It turns out that this case is exceptional: If for any infinitesimally-homogeneous tensor field $ A $ | ||
| + | of certain type there exists a unique torsion-free connection relative to which it is parallel, then the structure group $ G $ | ||
| + | of the $ G $- | ||
| + | structure $ P( A) $ | ||
| + | is pseudo-orthogonal, and consequently a pseudo-Riemannian metric is canonically associated with $ A $[[#References|[7]]]. For a broad class of infinitesimally-homogeneous tensor fields $ A $ | ||
| + | the presence of a torsion-free connection relative to which the field is parallel implies the integrability of $ A $, | ||
| + | that is, the existence of a local coordinate system in which the components of $ A $ | ||
| + | are constant. This is so, for example, for an almost-complex structure, for an almost-symplectic structure and for any field $ A $ | ||
| + | for which the structure group $ G $ | ||
| + | of the bundle $ P( A) $ | ||
| + | is irreducible and does not belong to the known list of irreducible holonomy groups of spaces with a torsion-free linear connection. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , '''1–2''' , Interscience (1963–1969) {{MR|1393941}} {{MR|1393940}} {{MR|0238225}} {{MR|1533559}} {{MR|0152974}} {{ZBL|0526.53001}} {{ZBL|0508.53002}} {{ZBL|0175.48504}} {{ZBL|0119.37502}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A. Lichnerowicz, "Global theory of connections and holonomy groups" , Noordhoff (1976) (Translated from French) {{MR|0413000}} {{ZBL|0337.53031}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S.S. Chern, "Complex manifolds without potential theory" , Springer (1979) {{MR|0533884}} {{ZBL|0444.32004}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> S.-S. Chern, "On a generalization of Kähler geometry" R.H. Fox (ed.) D.C. Spencer (ed.) A.W. Tucker (ed.) , ''Algebraic geometry and topology (Symp. in honor of S. Lefschetz)'' , Princeton Univ. Press (1957) pp. 103–121 {{MR|0087172}} {{ZBL|0078.14103}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> M. Berger, "Sur les groupes d'holonomie homogène des variétés à connexion affine et des variétés riemanniennes" ''Bull. Soc. Math. France'' , '''83''' (1955) pp. 279–330 {{MR|0079806}} {{ZBL|}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> S. Kobayashi, "Transformation groups in differential geometry" , Springer (1972) {{MR|0355886}} {{ZBL|0246.53031}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> S. Kobayashi, T. Nagano, "On a fundamental theorem of Weyl–Cartan on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071350/p07135077.png" />-structures" ''J. Math. Soc. Japan'' , '''17''' (1965) pp. 84–101 {{MR|192438}} {{ZBL|}} </TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , '''1–2''' , Interscience (1963–1969) {{MR|1393941}} {{MR|1393940}} {{MR|0238225}} {{MR|1533559}} {{MR|0152974}} {{ZBL|0526.53001}} {{ZBL|0508.53002}} {{ZBL|0175.48504}} {{ZBL|0119.37502}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A. Lichnerowicz, "Global theory of connections and holonomy groups" , Noordhoff (1976) (Translated from French) {{MR|0413000}} {{ZBL|0337.53031}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S.S. Chern, "Complex manifolds without potential theory" , Springer (1979) {{MR|0533884}} {{ZBL|0444.32004}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> S.-S. Chern, "On a generalization of Kähler geometry" R.H. Fox (ed.) D.C. Spencer (ed.) A.W. Tucker (ed.) , ''Algebraic geometry and topology (Symp. in honor of S. Lefschetz)'' , Princeton Univ. Press (1957) pp. 103–121 {{MR|0087172}} {{ZBL|0078.14103}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> M. Berger, "Sur les groupes d'holonomie homogène des variétés à connexion affine et des variétés riemanniennes" ''Bull. Soc. Math. France'' , '''83''' (1955) pp. 279–330 {{MR|0079806}} {{ZBL|}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> S. Kobayashi, "Transformation groups in differential geometry" , Springer (1972) {{MR|0355886}} {{ZBL|0246.53031}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> S. Kobayashi, T. Nagano, "On a fundamental theorem of Weyl–Cartan on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071350/p07135077.png" />-structures" ''J. Math. Soc. Japan'' , '''17''' (1965) pp. 84–101 {{MR|192438}} {{ZBL|}} </TD></TR></table> | ||
Latest revision as of 08:05, 6 June 2020
covariantly-constant field
A tensor field $ A $( cf. Tensor analysis) on a manifold $ M $ with a linear connection $ \nabla $ that is invariant under parallel displacement along curves on $ M $. This means that for any points $ p, q \in M $ the tensor $ A _ {p} $( the value of the tensor field $ A $ at the point $ p $) under the parallel displacement to $ q $ along any smooth curve joining $ p $ and $ q $ transforms to the tensor $ A _ {q} $.
A tensor field $ A $ is parallel if and only if its covariant derivative in the direction of any vector field $ X $ vanishes identically: $ \nabla _ {X} A = 0 $ or, in other words, if the covariant differential $ DA $ of $ A $ vanishes.
The set $ \Pi ( M, \nabla ) $ of parallel fields forms a subalgebra of the algebra of all tensor fields on $ M $ that is invariant under contraction of tensor fields and permutation of their indices. The algebra $ \Pi ( M, \nabla ) $ is naturally isomorphic to the algebra of tensors at a fixed point $ p $ of $ M $ that are invariant under the homogeneous holonomy group $ M _ {p} $ of $ \nabla $ at $ p $. For a connection with full holonomy group $ \Gamma = \mathop{\rm GL} ( n, \mathbf R ) $, where $ n = \mathop{\rm dim} M $, the algebra $ \Pi ( M, \nabla ) $ is generated by the Kronecker symbol $ \delta _ {j} ^ {i} $; for a Riemannian connection with holonomy group $ \textrm{ O } ( n) $— by the metric tensor $ g = ( g _ {ij} ) $ and its inverse $ g ^ {-} 1 = ( g ^ {ij} ) $, and for a Riemannian connection with holonomy group $ \mathop{\rm SO} ( n) $— by the tensors $ g $ and $ g ^ {-} 1 $ and the volume $ n $- form. There are also descriptions of the generators of the algebra of parallel differential forms on an arbitrary space with a torsion-free linear connection with an arbitrary irreducible holonomy group [5].
Of special interest are the parallel fields of differential forms on a Riemannian manifold with a Levi-Civita connection. With every such form $ \omega $ there is associated (by means of the tensor product with respect to $ \omega $ and contractions) a number of linear operators in the space of differential forms that commute with the Laplace–Beltrami operator $ \Delta $, for example, the operator of interior and exterior multiplication by $ \omega $ or the operator of orthogonal projection onto subspaces of the space of differential forms that are invariant relative to the holonomy group. The study of these operators makes it possible to obtain estimates for the dimensions of the spaces of harmonic forms of various degrees, that is, (in the compact case) for the Betti numbers of $ M $( see [4]). The most substantial theory (see Hodge theorem) has been developed for Kähler and for quaternion Kähler manifolds (cf. Kähler manifold), in which there always is a parallel field of $ 2 $- forms, respectively, of $ 4 $- forms. Any parallel differential form in a Riemannian space is harmonic. In a compact symmetric Riemannian space the converse is true: Any harmonic form is parallel. Therefore, the real cohomology ring of a compact symmetric space is isomorphic to the ring of parallel differential forms.
A tensor field $ A $ is a parallel field, relative to some linear connection $ \nabla $, if and only if it is infinitesimally homogeneous, that is, if at every point $ p $ of $ M $ there is a frame relative to which the tensor $ A _ {p} $ has fixed components $ A _ {j _ {1} \dots j _ {l} } ^ {i _ {1} \dots i _ {k} } $ independent of $ p $. In this case the set of frames relative to which the tensors $ A _ {p} $, $ p \in M $, have the components $ A _ {j _ {1} \dots j _ {l} } ^ {i _ {1} \dots i _ {k} } $ form a $ G $- structure, that is, the principal subbundle $ P( A) $ of the bundle of frames with the structure group $ G $, where $ G $ is the stabilizer of $ A _ {p} $ under the action of the group $ \mathop{\rm GL} ( n, \mathbf R ) $ on the tensor space. The field $ A $ is parallel relative to any connection in the $ G $- structure $ P( A) $. In particular, any section of $ P( A) $( if it exists) gives a connection with zero curvature relative to which $ A $ is a parallel field.
More complicated is the problem of the existence of torsion-free connections relative to which a given infinitesimally-homogeneous field is parallel. If $ A $ has a pseudo-Riemannian metric, then such a connection (a Levi-Civita connection) always exists, and is unique. It turns out that this case is exceptional: If for any infinitesimally-homogeneous tensor field $ A $ of certain type there exists a unique torsion-free connection relative to which it is parallel, then the structure group $ G $ of the $ G $- structure $ P( A) $ is pseudo-orthogonal, and consequently a pseudo-Riemannian metric is canonically associated with $ A $[7]. For a broad class of infinitesimally-homogeneous tensor fields $ A $ the presence of a torsion-free connection relative to which the field is parallel implies the integrability of $ A $, that is, the existence of a local coordinate system in which the components of $ A $ are constant. This is so, for example, for an almost-complex structure, for an almost-symplectic structure and for any field $ A $ for which the structure group $ G $ of the bundle $ P( A) $ is irreducible and does not belong to the known list of irreducible holonomy groups of spaces with a torsion-free linear connection.
References
| [1] | S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 1–2 , Interscience (1963–1969) MR1393941 MR1393940 MR0238225 MR1533559 MR0152974 Zbl 0526.53001 Zbl 0508.53002 Zbl 0175.48504 Zbl 0119.37502 |
| [2] | A. Lichnerowicz, "Global theory of connections and holonomy groups" , Noordhoff (1976) (Translated from French) MR0413000 Zbl 0337.53031 |
| [3] | S.S. Chern, "Complex manifolds without potential theory" , Springer (1979) MR0533884 Zbl 0444.32004 |
| [4] | S.-S. Chern, "On a generalization of Kähler geometry" R.H. Fox (ed.) D.C. Spencer (ed.) A.W. Tucker (ed.) , Algebraic geometry and topology (Symp. in honor of S. Lefschetz) , Princeton Univ. Press (1957) pp. 103–121 MR0087172 Zbl 0078.14103 |
| [5] | M. Berger, "Sur les groupes d'holonomie homogène des variétés à connexion affine et des variétés riemanniennes" Bull. Soc. Math. France , 83 (1955) pp. 279–330 MR0079806 |
| [6] | S. Kobayashi, "Transformation groups in differential geometry" , Springer (1972) MR0355886 Zbl 0246.53031 |
| [7] | S. Kobayashi, T. Nagano, "On a fundamental theorem of Weyl–Cartan on 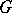 -structures" J. Math. Soc. Japan , 17 (1965) pp. 84–101 MR192438 -structures" J. Math. Soc. Japan , 17 (1965) pp. 84–101 MR192438 |
Parallel field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Parallel_field&oldid=48116