Difference between revisions of "Non-central chi-squared distribution"
Ulf Rehmann (talk | contribs) m (dead link removed) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | n0669602.png | ||
| + | $#A+1 = 26 n = 2 | ||
| + | $#C+1 = 26 : ~/encyclopedia/old_files/data/N066/N.0606960 Non\AAhcentral \BQT chi\AAhsquared\EQT distribution, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | ''non-central $ \chi ^ {2} $- | |
| + | distribution'' | ||
| − | + | A continuous probability distribution concentrated on the positive semi-axis $ 0 < x < \infty $ | |
| + | with density | ||
| − | + | $$ | |
| − | + | \frac{e ^ {- ( x + \lambda ) / 2 } x ^ {( n - 2 ) / 2 } }{2 ^ {n / 2 } \Gamma ( 1 / 2 ) } | |
| − | + | \sum _ {r = 0 } ^ \infty | |
| − | + | \frac{\lambda ^ {r} x ^ {r} }{( 2 r ) ! } | |
| − | + | \frac{\Gamma ( r + 1 / 2 ) }{\Gamma ( r + n / 2 ) } | |
| + | , | ||
| + | $$ | ||
| − | + | where $ n $ | |
| + | is the number of degrees of freedom and $ \lambda $ | ||
| + | the parameter of non-centrality. For $ \lambda = 0 $ | ||
| + | this density is that of the ordinary (central) [[Chi-squared distribution| "chi-squared" distribution]]. The [[Characteristic function|characteristic function]] of a non-central "chi-squared" distribution is | ||
| − | + | $$ | |
| + | \phi ( t) = ( 1 - 2 i t ) ^ {-} n/2 \mathop{\rm exp} | ||
| + | \left \{ | ||
| + | \frac{\lambda i t }{1 - 2 i t } | ||
| + | \right \} ; | ||
| + | $$ | ||
| + | |||
| + | the [[Mathematical expectation|mathematical expectation]] and variance (cf. [[Dispersion|Dispersion]]) are $ n + \lambda $ | ||
| + | and $ 2 ( n + 2 \lambda ) $, | ||
| + | respectively. A non-central "chi-squared" distribution belongs to the class of infinitely-divisible distributions (cf. [[Infinitely-divisible distribution|Infinitely-divisible distribution]]). | ||
| + | |||
| + | As a rule, a non-central "chi-squared" distribution appears as the distribution of the sum of squares of independent random variables $ X _ {1} \dots X _ {n} $ | ||
| + | having normal distributions with non-zero means $ m _ {i} $ | ||
| + | and unit variance; more precisely, the sum $ X _ {1} ^ {2} + \dots X _ {n} ^ {2} $ | ||
| + | has a non-central "chi-squared" distribution with $ n $ | ||
| + | degrees of freedom and non-centrality parameter $ \lambda = \sum _ {i=} 1 ^ {n} m _ {i} ^ {2} $. | ||
| + | The sum of several mutually independent random variables with a non-central "chi-squared" distribution has a distribution of the same type and its parameters are the sums of the corresponding parameters of the summands. | ||
| + | |||
| + | If $ n $ | ||
| + | is even, then the distribution function of a non-central "chi-squared" distribution $ F _ {n} ( x ; \lambda ) $ | ||
| + | is given by $ F _ {n} ( x ; \lambda ) = 0 $ | ||
| + | for $ x \leq 0 $ | ||
| + | and for $ x > 0 $ | ||
| + | by | ||
| + | |||
| + | $$ | ||
| + | F _ {n} ( x ; \lambda ) = \ | ||
| + | \sum _ { m= } 0 ^ \infty \ | ||
| + | \sum _ {k = m + n / 2 } ^ \infty | ||
| + | |||
| + | \frac{( \lambda / 2 ) ^ {m} ( x / 2 ) ^ {k} }{m ! k ! } | ||
| + | |||
| + | e ^ {- ( \lambda + x ) / 2 } . | ||
| + | $$ | ||
| + | |||
| + | This formula establishes a link between a non-central "chi-squared" distribution and a [[Poisson distribution|Poisson distribution]]. Namely, if $ X $ | ||
| + | and $ Y $ | ||
| + | have Poisson distributions with parameters $ x / 2 $ | ||
| + | and $ \lambda / 2 $, | ||
| + | respectively, then for any positive integer $ s > 0 $, | ||
| + | |||
| + | $$ | ||
| + | {\mathsf P} \{ X - Y \geq s \} = F _ {2s} ( x ; \lambda ) . | ||
| + | $$ | ||
A non-central "chi-squared" distribution often arises in problems of mathematical statistics concerned with the study of the power of tests of "chi-squared" type. Since tables of non-central "chi-squared" distributions are fairly complete, various approximations by means of a "chi-squared" and a normal distribution are widely used in statistical applications. | A non-central "chi-squared" distribution often arises in problems of mathematical statistics concerned with the study of the power of tests of "chi-squared" type. Since tables of non-central "chi-squared" distributions are fairly complete, various approximations by means of a "chi-squared" and a normal distribution are widely used in statistical applications. | ||
| Line 25: | Line 83: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , ''Libr. math. tables'' , '''46''' , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M.G. Kendall, A. Stuart, "The advanced theory of statistics" , '''2. Inference and relationship''' , Griffin (1979)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> P.B. Patnaik, "The non-central <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066960/n06696028.png" />- and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066960/n06696029.png" />-distributions and their applications" ''Biometrica'' , '''36''' (1949) pp. 202–232</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , ''Libr. math. tables'' , '''46''' , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M.G. Kendall, A. Stuart, "The advanced theory of statistics" , '''2. Inference and relationship''' , Griffin (1979)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> P.B. Patnaik, "The non-central <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066960/n06696028.png" />- and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066960/n06696029.png" />-distributions and their applications" ''Biometrica'' , '''36''' (1949) pp. 202–232</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> N.L. Johnson, S. Kotz, "Distributions in statistics" , '''2. Continuous univariate distributions''' , Wiley (1970)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> N.L. Johnson, S. Kotz, "Distributions in statistics" , '''2. Continuous univariate distributions''' , Wiley (1970)</TD></TR></table> | ||
Revision as of 08:03, 6 June 2020
non-central $ \chi ^ {2} $-
distribution
A continuous probability distribution concentrated on the positive semi-axis $ 0 < x < \infty $ with density
$$ \frac{e ^ {- ( x + \lambda ) / 2 } x ^ {( n - 2 ) / 2 } }{2 ^ {n / 2 } \Gamma ( 1 / 2 ) } \sum _ {r = 0 } ^ \infty \frac{\lambda ^ {r} x ^ {r} }{( 2 r ) ! } \frac{\Gamma ( r + 1 / 2 ) }{\Gamma ( r + n / 2 ) } , $$
where $ n $ is the number of degrees of freedom and $ \lambda $ the parameter of non-centrality. For $ \lambda = 0 $ this density is that of the ordinary (central) "chi-squared" distribution. The characteristic function of a non-central "chi-squared" distribution is
$$ \phi ( t) = ( 1 - 2 i t ) ^ {-} n/2 \mathop{\rm exp} \left \{ \frac{\lambda i t }{1 - 2 i t } \right \} ; $$
the mathematical expectation and variance (cf. Dispersion) are $ n + \lambda $ and $ 2 ( n + 2 \lambda ) $, respectively. A non-central "chi-squared" distribution belongs to the class of infinitely-divisible distributions (cf. Infinitely-divisible distribution).
As a rule, a non-central "chi-squared" distribution appears as the distribution of the sum of squares of independent random variables $ X _ {1} \dots X _ {n} $ having normal distributions with non-zero means $ m _ {i} $ and unit variance; more precisely, the sum $ X _ {1} ^ {2} + \dots X _ {n} ^ {2} $ has a non-central "chi-squared" distribution with $ n $ degrees of freedom and non-centrality parameter $ \lambda = \sum _ {i=} 1 ^ {n} m _ {i} ^ {2} $. The sum of several mutually independent random variables with a non-central "chi-squared" distribution has a distribution of the same type and its parameters are the sums of the corresponding parameters of the summands.
If $ n $ is even, then the distribution function of a non-central "chi-squared" distribution $ F _ {n} ( x ; \lambda ) $ is given by $ F _ {n} ( x ; \lambda ) = 0 $ for $ x \leq 0 $ and for $ x > 0 $ by
$$ F _ {n} ( x ; \lambda ) = \ \sum _ { m= } 0 ^ \infty \ \sum _ {k = m + n / 2 } ^ \infty \frac{( \lambda / 2 ) ^ {m} ( x / 2 ) ^ {k} }{m ! k ! } e ^ {- ( \lambda + x ) / 2 } . $$
This formula establishes a link between a non-central "chi-squared" distribution and a Poisson distribution. Namely, if $ X $ and $ Y $ have Poisson distributions with parameters $ x / 2 $ and $ \lambda / 2 $, respectively, then for any positive integer $ s > 0 $,
$$ {\mathsf P} \{ X - Y \geq s \} = F _ {2s} ( x ; \lambda ) . $$
A non-central "chi-squared" distribution often arises in problems of mathematical statistics concerned with the study of the power of tests of "chi-squared" type. Since tables of non-central "chi-squared" distributions are fairly complete, various approximations by means of a "chi-squared" and a normal distribution are widely used in statistical applications.
References
| [1] | L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova) |
| [2] | M.G. Kendall, A. Stuart, "The advanced theory of statistics" , 2. Inference and relationship , Griffin (1979) |
| [3] | P.B. Patnaik, "The non-central 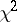 - and - and 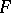 -distributions and their applications" Biometrica , 36 (1949) pp. 202–232 -distributions and their applications" Biometrica , 36 (1949) pp. 202–232 |
Comments
References
| [a1] | N.L. Johnson, S. Kotz, "Distributions in statistics" , 2. Continuous univariate distributions , Wiley (1970) |
Non-central chi-squared distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Non-central_chi-squared_distribution&oldid=47985