|
|
| Line 1: |
Line 1: |
| | + | <!-- |
| | + | m0652401.png |
| | + | $#A+1 = 90 n = 1 |
| | + | $#C+1 = 90 : ~/encyclopedia/old_files/data/M065/M.0605240 Multi\AAhvalued mapping, |
| | + | Automatically converted into TeX, above some diagnostics. |
| | + | Please remove this comment and the {{TEX|auto}} line below, |
| | + | if TeX found to be correct. |
| | + | --> |
| | + | |
| | + | {{TEX|auto}} |
| | + | {{TEX|done}} |
| | + | |
| | ''point-to-set mapping'' | | ''point-to-set mapping'' |
| | | | |
| − | A mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m0652401.png" /> associating with each element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m0652402.png" /> of a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m0652403.png" /> a subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m0652404.png" /> of a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m0652405.png" />. If for each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m0652406.png" /> the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m0652407.png" /> consists of one element, then the mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m0652408.png" /> is called single-valued. A multi-valued mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m0652409.png" /> can be treated as a single-valued mapping of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524010.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524011.png" />, that is, into the set of all subsets of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524012.png" />. | + | A mapping $ \Gamma : X \rightarrow Y $ |
| | + | associating with each element $ x $ |
| | + | of a set $ X $ |
| | + | a subset $ \Gamma ( x) $ |
| | + | of a set $ Y $. |
| | + | If for each $ x \in X $ |
| | + | the set $ \Gamma ( x) $ |
| | + | consists of one element, then the mapping $ \Gamma $ |
| | + | is called single-valued. A multi-valued mapping $ \Gamma $ |
| | + | can be treated as a single-valued mapping of $ X $ |
| | + | into $ 2 ^ {Y} $, |
| | + | that is, into the set of all subsets of $ Y $. |
| | | | |
| − | For two multi-valued mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524013.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524014.png" />, their inclusion is naturally defined: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524015.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524016.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524017.png" />. For any family of multi-valued mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524018.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524019.png" />, the union and intersection are defined: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524020.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524021.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524022.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524023.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524024.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524025.png" />. For any family of multi-valued mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524026.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524027.png" />, the multi-valued mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524028.png" /> is called the Cartesian product of the multi-valued mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524029.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524030.png" />. A section of a multi-valued mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524031.png" /> is a single-valued mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524032.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524033.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524034.png" />. The graph of a multi-valued mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524035.png" /> is the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524036.png" />. | + | For two multi-valued mappings $ \Gamma _ {i} : X \rightarrow Y $, |
| | + | $ i = 1 , 2 $, |
| | + | their inclusion is naturally defined: $ \Gamma _ {1} \subset \Gamma _ {2} $ |
| | + | if $ \Gamma _ {1} ( x) \subset \Gamma _ {2} ( x) $ |
| | + | for all $ x \in X $. |
| | + | For any family of multi-valued mappings $ \Gamma _ \alpha : X \rightarrow Y $, |
| | + | $ \alpha \in A $, |
| | + | the union and intersection are defined: $ \Gamma = \cup _ {\alpha \in A } \Gamma _ \alpha $ |
| | + | if $ \Gamma ( x) = \cup _ {\alpha \in A } \Gamma _ \alpha ( x) $ |
| | + | for all $ x \in X $ |
| | + | and $ \Gamma = \cap _ {\alpha \in A } \Gamma _ \alpha $ |
| | + | if $ \Gamma ( x) = \cap _ {\alpha \in A } \Gamma _ \alpha ( x) $ |
| | + | for all $ x \in X $. |
| | + | For any family of multi-valued mappings $ \Gamma _ \alpha : X \rightarrow Y _ \alpha $, |
| | + | $ \alpha \in A $, |
| | + | the multi-valued mapping $ \Gamma = \prod _ {\alpha \in A } \Gamma _ \alpha : X \rightarrow \prod _ {\alpha \in A } Y _ \alpha $ |
| | + | is called the Cartesian product of the multi-valued mappings $ \Gamma _ \alpha $ |
| | + | if $ \Gamma ( x) = \prod _ {\alpha \in A } \Gamma _ \alpha ( x) $. |
| | + | A section of a multi-valued mapping $ \Gamma $ |
| | + | is a single-valued mapping $ f : X \rightarrow Y $ |
| | + | such that $ f ( x) \in \Gamma ( x) $ |
| | + | for all $ x \in X $. |
| | + | The graph of a multi-valued mapping $ \Gamma $ |
| | + | is the set $ G ( \Gamma ) = \{ {( x , y ) \in X \times Y } : {y \in \Gamma ( x) } \} $. |
| | | | |
| − | A multi-valued mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524037.png" /> of a topological space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524038.png" /> into a topological space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524039.png" /> is called upper semi-continuous if for every open set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524040.png" /> the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524041.png" /> is open in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524042.png" />, or equivalently: For any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524043.png" /> and any neighbourhood <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524044.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524045.png" /> there is a neighbourhood <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524046.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524047.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524048.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524049.png" />. A multi-valued mapping from a topological space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524050.png" /> to a topological space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524051.png" /> is called lower semi-continuous if for any open set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524052.png" /> the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524053.png" /> is open in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524054.png" />. If a multi-valued mapping satisfies both properties simultaneously, then it is called a continuous multi-valued mapping. | + | A multi-valued mapping $ \Gamma $ |
| | + | of a topological space $ X $ |
| | + | into a topological space $ Y $ |
| | + | is called upper semi-continuous if for every open set $ U \subset Y $ |
| | + | the set $ \Gamma ^ {+} ( u) = \{ {x \in X } : {\Gamma ( x) \subset U, \Gamma ( x) \neq \emptyset } \} $ |
| | + | is open in $ X $, |
| | + | or equivalently: For any $ x \in X $ |
| | + | and any neighbourhood $ U $ |
| | + | of $ \Gamma ( x) $ |
| | + | there is a neighbourhood $ O x $ |
| | + | of $ x $ |
| | + | such that $ \Gamma ( Ox) \subset U $, |
| | + | where $ \Gamma ( Ox ) = \cup \{ {\Gamma ( y) } : {y \in Ox } \} $. |
| | + | A multi-valued mapping from a topological space $ X $ |
| | + | to a topological space $ Y $ |
| | + | is called lower semi-continuous if for any open set $ U \subset Y $ |
| | + | the set $ \Gamma ^ {-} ( U) = \{ {x \in X } : {\Gamma ( x) \cap U \neq \emptyset } \} $ |
| | + | is open in $ X $. |
| | + | If a multi-valued mapping satisfies both properties simultaneously, then it is called a continuous multi-valued mapping. |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524055.png" /> be a topological vector space. A multi-valued mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524056.png" /> is called convex-compact valued if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524057.png" /> is a convex compact set for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524058.png" />. For a finite set of multi-valued mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524059.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524060.png" />, the algebraic sum <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524061.png" /> is defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524062.png" />. The intersection of any (finite) family of upper semi-continuous (respectively, continuous) multi-valued mappings is upper semi-continuous (respectively, continuous). The Cartesian product of a finite family of upper semi-continuous multi-valued mappings is upper semi-continuous. The algebraic sum of a finite family of upper semi-continuous (convex-compact valued) mappings is upper semi-continuous (convex-compact valued). The intersection and Cartesian product of any family of convex-compact valued mappings is convex-compact valued. | + | Let $ Y $ |
| | + | be a topological vector space. A multi-valued mapping $ \Gamma : X\rightarrow Y $ |
| | + | is called convex-compact valued if $ \Gamma ( x) $ |
| | + | is a convex compact set for all $ x \in X $. |
| | + | For a finite set of multi-valued mappings $ \Gamma _ {i} : X \rightarrow Y $, |
| | + | $ i \in I $, |
| | + | the algebraic sum $ \Gamma = \sum _ {i \in I } \Gamma _ {i} $ |
| | + | is defined by $ \Gamma ( x) = \sum _ {i \in I } \Gamma _ {i} ( x) $. |
| | + | The intersection of any (finite) family of upper semi-continuous (respectively, continuous) multi-valued mappings is upper semi-continuous (respectively, continuous). The Cartesian product of a finite family of upper semi-continuous multi-valued mappings is upper semi-continuous. The algebraic sum of a finite family of upper semi-continuous (convex-compact valued) mappings is upper semi-continuous (convex-compact valued). The intersection and Cartesian product of any family of convex-compact valued mappings is convex-compact valued. |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524063.png" /> be a [[Paracompact space|paracompact space]] and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524064.png" /> a locally convex metric linear space (cf. [[Locally convex space|Locally convex space]]; [[Linear space|Linear space]]; [[Metric space|Metric space]]). Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524065.png" /> be a multi-valued mapping which is upper semi-continuous and is such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524066.png" /> is closed in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524067.png" /> for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524068.png" />. Then the multi-valued mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524069.png" /> admits continuous sections. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524070.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524071.png" /> be spaces with given <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524072.png" />-algebras <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524073.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524074.png" />; a multi-valued mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524075.png" /> is called measurable if the graph <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524076.png" /> belongs to the smallest <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524077.png" />-algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524078.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524079.png" /> containing all sets of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524080.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524081.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524082.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524083.png" /> is a measurable multi-valued mapping from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524084.png" /> to a complete separable metric space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524085.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524086.png" /> is the Borel <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524087.png" />-algebra of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524088.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524089.png" /> has measurable sections <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065240/m06524090.png" />. | + | Let $ X $ |
| | + | be a [[Paracompact space|paracompact space]] and $ Y $ |
| | + | a locally convex metric linear space (cf. [[Locally convex space|Locally convex space]]; [[Linear space|Linear space]]; [[Metric space|Metric space]]). Let $ \Gamma : X \rightarrow Y $ |
| | + | be a multi-valued mapping which is upper semi-continuous and is such that $ \Gamma ( x) $ |
| | + | is closed in $ Y $ |
| | + | for every $ x \in X $. |
| | + | Then the multi-valued mapping $ \Gamma $ |
| | + | admits continuous sections. Let $ ( X , \mathfrak A ) $ |
| | + | and $ ( Y , \mathfrak B ) $ |
| | + | be spaces with given $ \sigma $- |
| | + | algebras $ \mathfrak A $ |
| | + | and $ \mathfrak B $; |
| | + | a multi-valued mapping $ \Gamma : ( X , \mathfrak A ) \rightarrow ( Y , \mathfrak B ) $ |
| | + | is called measurable if the graph $ G ( \Gamma ) $ |
| | + | belongs to the smallest $ \sigma $- |
| | + | algebra $ \mathfrak A \times \mathfrak B $ |
| | + | of $ X \times Y $ |
| | + | containing all sets of the form $ A \times B $, |
| | + | where $ A \in \mathfrak A $ |
| | + | and $ B \in \mathfrak B $. |
| | + | If $ \Gamma $ |
| | + | is a measurable multi-valued mapping from $ ( X , \mathfrak A ) $ |
| | + | to a complete separable metric space $ ( Y , \mathfrak B ) $, |
| | + | where $ \mathfrak B $ |
| | + | is the Borel $ \sigma $- |
| | + | algebra of $ Y $, |
| | + | then $ \Gamma $ |
| | + | has measurable sections $ f $. |
| | | | |
| | ====References==== | | ====References==== |
| | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> K. Kuratowski, "Topology" , '''1–2''' , Acad. Press (1966–1968) (Translated from French)</TD></TR></table> | | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> K. Kuratowski, "Topology" , '''1–2''' , Acad. Press (1966–1968) (Translated from French)</TD></TR></table> |
| − |
| |
| − |
| |
| | | | |
| | ====Comments==== | | ====Comments==== |
point-to-set mapping
A mapping $ \Gamma : X \rightarrow Y $
associating with each element $ x $
of a set $ X $
a subset $ \Gamma ( x) $
of a set $ Y $.
If for each $ x \in X $
the set $ \Gamma ( x) $
consists of one element, then the mapping $ \Gamma $
is called single-valued. A multi-valued mapping $ \Gamma $
can be treated as a single-valued mapping of $ X $
into $ 2 ^ {Y} $,
that is, into the set of all subsets of $ Y $.
For two multi-valued mappings $ \Gamma _ {i} : X \rightarrow Y $,
$ i = 1 , 2 $,
their inclusion is naturally defined: $ \Gamma _ {1} \subset \Gamma _ {2} $
if $ \Gamma _ {1} ( x) \subset \Gamma _ {2} ( x) $
for all $ x \in X $.
For any family of multi-valued mappings $ \Gamma _ \alpha : X \rightarrow Y $,
$ \alpha \in A $,
the union and intersection are defined: $ \Gamma = \cup _ {\alpha \in A } \Gamma _ \alpha $
if $ \Gamma ( x) = \cup _ {\alpha \in A } \Gamma _ \alpha ( x) $
for all $ x \in X $
and $ \Gamma = \cap _ {\alpha \in A } \Gamma _ \alpha $
if $ \Gamma ( x) = \cap _ {\alpha \in A } \Gamma _ \alpha ( x) $
for all $ x \in X $.
For any family of multi-valued mappings $ \Gamma _ \alpha : X \rightarrow Y _ \alpha $,
$ \alpha \in A $,
the multi-valued mapping $ \Gamma = \prod _ {\alpha \in A } \Gamma _ \alpha : X \rightarrow \prod _ {\alpha \in A } Y _ \alpha $
is called the Cartesian product of the multi-valued mappings $ \Gamma _ \alpha $
if $ \Gamma ( x) = \prod _ {\alpha \in A } \Gamma _ \alpha ( x) $.
A section of a multi-valued mapping $ \Gamma $
is a single-valued mapping $ f : X \rightarrow Y $
such that $ f ( x) \in \Gamma ( x) $
for all $ x \in X $.
The graph of a multi-valued mapping $ \Gamma $
is the set $ G ( \Gamma ) = \{ {( x , y ) \in X \times Y } : {y \in \Gamma ( x) } \} $.
A multi-valued mapping $ \Gamma $
of a topological space $ X $
into a topological space $ Y $
is called upper semi-continuous if for every open set $ U \subset Y $
the set $ \Gamma ^ {+} ( u) = \{ {x \in X } : {\Gamma ( x) \subset U, \Gamma ( x) \neq \emptyset } \} $
is open in $ X $,
or equivalently: For any $ x \in X $
and any neighbourhood $ U $
of $ \Gamma ( x) $
there is a neighbourhood $ O x $
of $ x $
such that $ \Gamma ( Ox) \subset U $,
where $ \Gamma ( Ox ) = \cup \{ {\Gamma ( y) } : {y \in Ox } \} $.
A multi-valued mapping from a topological space $ X $
to a topological space $ Y $
is called lower semi-continuous if for any open set $ U \subset Y $
the set $ \Gamma ^ {-} ( U) = \{ {x \in X } : {\Gamma ( x) \cap U \neq \emptyset } \} $
is open in $ X $.
If a multi-valued mapping satisfies both properties simultaneously, then it is called a continuous multi-valued mapping.
Let $ Y $
be a topological vector space. A multi-valued mapping $ \Gamma : X\rightarrow Y $
is called convex-compact valued if $ \Gamma ( x) $
is a convex compact set for all $ x \in X $.
For a finite set of multi-valued mappings $ \Gamma _ {i} : X \rightarrow Y $,
$ i \in I $,
the algebraic sum $ \Gamma = \sum _ {i \in I } \Gamma _ {i} $
is defined by $ \Gamma ( x) = \sum _ {i \in I } \Gamma _ {i} ( x) $.
The intersection of any (finite) family of upper semi-continuous (respectively, continuous) multi-valued mappings is upper semi-continuous (respectively, continuous). The Cartesian product of a finite family of upper semi-continuous multi-valued mappings is upper semi-continuous. The algebraic sum of a finite family of upper semi-continuous (convex-compact valued) mappings is upper semi-continuous (convex-compact valued). The intersection and Cartesian product of any family of convex-compact valued mappings is convex-compact valued.
Let $ X $
be a paracompact space and $ Y $
a locally convex metric linear space (cf. Locally convex space; Linear space; Metric space). Let $ \Gamma : X \rightarrow Y $
be a multi-valued mapping which is upper semi-continuous and is such that $ \Gamma ( x) $
is closed in $ Y $
for every $ x \in X $.
Then the multi-valued mapping $ \Gamma $
admits continuous sections. Let $ ( X , \mathfrak A ) $
and $ ( Y , \mathfrak B ) $
be spaces with given $ \sigma $-
algebras $ \mathfrak A $
and $ \mathfrak B $;
a multi-valued mapping $ \Gamma : ( X , \mathfrak A ) \rightarrow ( Y , \mathfrak B ) $
is called measurable if the graph $ G ( \Gamma ) $
belongs to the smallest $ \sigma $-
algebra $ \mathfrak A \times \mathfrak B $
of $ X \times Y $
containing all sets of the form $ A \times B $,
where $ A \in \mathfrak A $
and $ B \in \mathfrak B $.
If $ \Gamma $
is a measurable multi-valued mapping from $ ( X , \mathfrak A ) $
to a complete separable metric space $ ( Y , \mathfrak B ) $,
where $ \mathfrak B $
is the Borel $ \sigma $-
algebra of $ Y $,
then $ \Gamma $
has measurable sections $ f $.
References
| [1] | K. Kuratowski, "Topology" , 1–2 , Acad. Press (1966–1968) (Translated from French) |
A multi-valued mapping is also called a set-valued or many-valued mapping. Sections are also called selections.
Theorems which prove that certain kinds of multi-valued mappings admit selections are called selection theorems. The measurable selection theorem stated in the last sentence of the main article above is known as von Neumann's measurable choice theorem. A number of selection theorems and some applications are discussed in [a4].
References
| [a1] | E. Michael, "Continuous selections" Ann. of Math. , 63 (1956) pp. 361–382 |
| [a2] | E.A. Michael, "A survey of continuous selections" W.M. Fleischmann (ed.) , Set valued mappings, selections and topological properties of 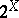 (Proc. Conf. SUNY Buffalo, 1969) , Lect. notes in math. , 171 , Springer (1970) pp. 54–58 (Proc. Conf. SUNY Buffalo, 1969) , Lect. notes in math. , 171 , Springer (1970) pp. 54–58 |
| [a3] | K. Przeslawski, D. Yost, "Continuity properties of selectors and Michael's Theorem" Mich. Math. J. , 36 (1989) pp. 113–134 |
| [a4] | T. Parthasarathy, "Selection theorems and their applications" , Lect. notes in math. , 263 , Springer (1972) |
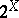 (Proc. Conf. SUNY Buffalo, 1969) , Lect. notes in math. , 171 , Springer (1970) pp. 54–58
(Proc. Conf. SUNY Buffalo, 1969) , Lect. notes in math. , 171 , Springer (1970) pp. 54–58