Difference between revisions of "Motives, theory of"
(Corrected wrong link) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | m0650401.png | ||
| + | $#A+1 = 79 n = 2 | ||
| + | $#C+1 = 79 : ~/encyclopedia/old_files/data/M065/M.0605040 Motives, theory of | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A generalization of the various [[Cohomology|cohomology]] theories of algebraic varieties. The theory of motives systematically generalizes the idea of using the [[Jacobi variety]] of an algebraic curve $ X $ | |
| + | as a replacement for the cohomology group $ H ^ {1} ( X , \mathbf Q ) $ | ||
| + | in the classical theory of correspondences, and the use of this theory in the study of the [[Zeta-function|zeta-function]] of a curve $ X $ | ||
| + | over a finite field. The theory of motives is universal in the sense that every geometric cohomology theory, of the type of the classical singular cohomology for algebraic varieties over $ \mathbf C $ | ||
| + | with constant coefficients, every $ l $- | ||
| + | adic cohomology theory for various prime numbers $ l $ | ||
| + | different from the characteristic of the ground field, every crystalline cohomology theory, etc. (see [[Weil cohomology|Weil cohomology]]) are functors on the category of motives. | ||
| − | + | Let $ V ( k) $ | |
| + | be the category of smooth projective varieties over a field $ k $ | ||
| + | and let $ X \rightarrow C ( X) $ | ||
| + | be a contravariant functor of global [[Intersection theory|intersection theory]] from $ V ( k) $ | ||
| + | into the category of commutative $ \Lambda $- | ||
| + | algebras, where $ \Lambda $ | ||
| + | is a fixed ring. For example, $ C ( X) $ | ||
| + | is the [[Chow ring|Chow ring]] of classes of algebraic cycles (cf. [[Algebraic cycle|Algebraic cycle]]) on $ X $ | ||
| + | modulo a suitable (rational, algebraic, numerical, etc.) equivalence relation, or $ C ( X) = K ( X) $ | ||
| + | is the Grothendieck ring, or $ C ( X) = H ^ {ev} ( X) $ | ||
| + | is the ring of cohomology classes of even dimension, etc. The category $ V ( k) $ | ||
| + | and the functor $ X \rightarrow C ( X) $ | ||
| + | enable one to define a new category, the category of correspondences $ C V ( k) $, | ||
| + | whose objects are varieties $ X \in V ( k) $, | ||
| + | denoted by $ \overline{X}\; $, | ||
| + | and whose morphisms are defined by the formula | ||
| − | + | $$ | |
| + | \mathop{\rm Hom} ( \overline{X}\; , \overline{Y}\; ) = C ( X \times Y ) | ||
| + | $$ | ||
| − | Let | + | with the usual composition law for correspondences (see [[#References|[1]]]). Let the functor $ C $ |
| + | take values in the category of commutative graded $ \Lambda $- | ||
| + | algebras $ A ( \Lambda ) $. | ||
| + | Then $ C V ( k) $ | ||
| + | will be the $ \Lambda $- | ||
| + | additive category of graded correspondences. Moreover, $ C V ( k) $ | ||
| + | will have direct sums and tensor products. | ||
| − | + | The category whose objects are the varieties from $ V ( k) $ | |
| + | and whose morphisms are correspondences of degree $ 0 $ | ||
| + | is denoted by $ C V ^ {0} ( k) $. | ||
| + | A natural functor from $ V ( k) $ | ||
| + | into $ C V ^ {0} ( k) $ | ||
| + | has been defined, and the functor $ C $ | ||
| + | extends to a functor $ T $ | ||
| + | from $ C V ^ {0} ( k) $ | ||
| + | to $ A ( \Lambda ) $. | ||
| + | The category $ C V ^ {0} ( k) $, | ||
| + | like $ C V ( k) $, | ||
| + | is not Abelian. Its pseudo-Abelian completion, the category $ M _ {C} ^ {+} ( k) $, | ||
| + | has been considered. It is obtained from $ C V ^ {0} ( k) $ | ||
| + | by the formal addition of the images of all projections $ p $. | ||
| + | More precisely, the objects of $ M _ {C} ^ {+} ( k) $ | ||
| + | are pairs $ ( \overline{X}\; , p ) $, | ||
| + | where $ \overline{X}\; \in C V ^ {0} ( k) $ | ||
| + | and $ p \in \mathop{\rm Hom} ( \overline{X}\; , \overline{X}\; ) $, | ||
| + | $ p ^ {2} = p $, | ||
| + | and $ H ( ( \overline{X}\; , p ) , ( \overline{Y}\; , q ) ) $ | ||
| + | is the set of correspondences $ f : \overline{X}\; \rightarrow \overline{Y}\; $ | ||
| + | such that $ f \circ p = = q \circ f $ | ||
| + | modulo a correspondence $ g $ | ||
| + | with $ g \circ p = p \circ g = 0 $. | ||
| + | The category $ C V ^ {0} ( k) $ | ||
| + | is imbedded in $ M _ {C} ^ {+} ( k) $ | ||
| + | by means of the functor $ \overline{X}\; \rightarrow ( \overline{X}\; , \mathop{\rm id} ) $. | ||
| + | The natural functor $ h : V ( k) \rightarrow M _ {C} ^ {+} ( k) $ | ||
| + | is called the functor of motive cohomology spaces and $ M _ {C} ^ {+} ( k) $ | ||
| + | is called the category of effective motives. | ||
| − | + | Let $ p = ( 1 \times e ) $, | |
| + | where $ e $ | ||
| + | is the class of any rational point on the projective line $ P ^ {1} $, | ||
| + | and let $ L = ( P ^ {1} , p ) $. | ||
| + | Then | ||
| − | + | $$ | |
| + | h ( P ^ {n} ) = 1 \oplus L \oplus | ||
| + | L ^ {\otimes _ {2} } \oplus \dots \oplus | ||
| + | L ^ {\otimes _ {n} } . | ||
| + | $$ | ||
| + | |||
| + | If $ X = P ( E) $ | ||
| + | is the projectivization of a locally free sheaf $ E $ | ||
| + | of rank $ r $ | ||
| + | on $ Y $, | ||
| + | then | ||
| + | |||
| + | $$ | ||
| + | h ( X) = \oplus _ {i = 0 } ^ { {r } - 1 } | ||
| + | ( h ( Y) \otimes L ^ {\otimes _ {i} } ) . | ||
| + | $$ | ||
Motives of a monodial transformation with a non-singular centre, motives of curves (see [[#References|[1]]]), motives of Abelian manifolds (see [[#References|[2]]]), and motives of Weil hypersurfaces have also been calculated. | Motives of a monodial transformation with a non-singular centre, motives of curves (see [[#References|[1]]]), motives of Abelian manifolds (see [[#References|[2]]]), and motives of Weil hypersurfaces have also been calculated. | ||
| − | The category of motives | + | The category of motives $ M _ {C} ( k) $ |
| + | is obtained from $ M _ {C} ^ {+} ( k) $ | ||
| + | by the formal addition of negative powers of the motives $ L $. | ||
| + | By analogy with [[L-adic-cohomology| $ l $- | ||
| + | adic cohomology]], $ T = L ^ {\otimes _ {-} 1 } $ | ||
| + | is called the Tate motive. Tensor multiplication with $ T $ | ||
| + | is called twisting by the Tate motive. Twisting enables one to define the level of a motive as in an $ l $- | ||
| + | adic cohomology theory. Any functor of the Weil cohomology factors through the functor $ h : V ( k) \rightarrow M _ {C} ( k) $. | ||
| + | There is the conjecture that $ M _ {C} ( k) $ | ||
| + | does not, in some sense, depend on the intersection theory of $ C $, | ||
| + | and that the functor $ X \rightarrow h ( X) $ | ||
| + | is itself a (universal) theory for the Weil cohomology. This conjecture is closely related to the standard Grothendieck conjectures (see [[#References|[5]]]) on algebraic cycles (at present, 1982, not proved). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> Yu.I. Manin, "Correspondences, motives and monoidal transformations" ''Math. USSR Sb.'' , '''6''' : 4 (1968) pp. 439–470 ''Mat. Sb.'' , '''77''' : 4 (1968) pp. 475–507</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.M. Shermenev, "The motif of an abelian variety" ''Uspekhi Mat. Nauk'' , '''26''' : 2 (1971) pp. 215–216 (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> M. Demazure, "Motives des variétés algébrique" , ''Sem. Bourbaki Exp. 365'' , ''Lect. notes in math.'' , '''180''' , Springer (1971) pp. 19–38</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> S.L. Kleiman, "Motives" P. Holm (ed.) , ''Algebraic Geom. Proc. 5-th Nordic Summer School Math. Oslo, 1970'' , Wolters-Noordhoff (1972) pp. 53–96</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> S.L. Kleiman, "Algebraic cycles and the Weil conjectures" A. Grothendieck (ed.) J. Giraud (ed.) et al. (ed.) , ''Dix exposés sur la cohomologie des schémas'' , North-Holland & Masson (1968) pp. 359–386</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> Yu.I. Manin, "Correspondences, motives and monoidal transformations" ''Math. USSR Sb.'' , '''6''' : 4 (1968) pp. 439–470 ''Mat. Sb.'' , '''77''' : 4 (1968) pp. 475–507</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.M. Shermenev, "The motif of an abelian variety" ''Uspekhi Mat. Nauk'' , '''26''' : 2 (1971) pp. 215–216 (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> M. Demazure, "Motives des variétés algébrique" , ''Sem. Bourbaki Exp. 365'' , ''Lect. notes in math.'' , '''180''' , Springer (1971) pp. 19–38</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> S.L. Kleiman, "Motives" P. Holm (ed.) , ''Algebraic Geom. Proc. 5-th Nordic Summer School Math. Oslo, 1970'' , Wolters-Noordhoff (1972) pp. 53–96</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> S.L. Kleiman, "Algebraic cycles and the Weil conjectures" A. Grothendieck (ed.) J. Giraud (ed.) et al. (ed.) , ''Dix exposés sur la cohomologie des schémas'' , North-Holland & Masson (1968) pp. 359–386</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | The theory of motives has been created by A. Grothendieck in the 1960-s. Although the above-mentioned standard conjectures on algebraic cycles have not yet (1989) been proved, the theory of motives has played an important role in various recent developments, for instance: i) as a guide for the Deligne–Hodge theory ([[#References|[a1]]]); ii) in the study of absolute Hodge cycles on Abelian varieties ([[#References|[a2]]]), where a variant of the notion of a motive has been used; iii) in the study of Chow groups on certain varieties over a finite field ([[#References|[a3]]]); and iv) in work on the Beilinson's conjectures on special values of | + | The theory of motives has been created by A. Grothendieck in the 1960-s. Although the above-mentioned standard conjectures on algebraic cycles have not yet (1989) been proved, the theory of motives has played an important role in various recent developments, for instance: i) as a guide for the Deligne–Hodge theory ([[#References|[a1]]]); ii) in the study of absolute Hodge cycles on Abelian varieties ([[#References|[a2]]]), where a variant of the notion of a motive has been used; iii) in the study of Chow groups on certain varieties over a finite field ([[#References|[a3]]]); and iv) in work on the Beilinson's conjectures on special values of $ L $- |
| + | functions (see [[#References|[a4]]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P. Deligne, "Theory de Hodge I" , ''Proc. Internat. Congress Mathematicians (Nice, 1970)'' , '''1''' , Gauthier-Villars (1971) pp. 425–430</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> P. Deligne (ed.) J.S. Milne (ed.) A. Ogus (ed.) K. Shih (ed.) , ''Hodge cycles, motives and Shimura varieties'' , ''Lect. notes in math.'' , '''900''' , Springer (1980)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> C. Soulé, "Groupes de Chow et <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m06504080.png" />-theory des variétés sur un corps fini" ''Math. Ann.'' , '''268''' (1984) pp. 317–345</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M. Rapoport (ed.) N. Schappacher (ed.) P. Schneider (ed.) , ''Beilinson's conjectures on special values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m06504081.png" />-functions'' , Acad. Press (1988)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P. Deligne, "Theory de Hodge I" , ''Proc. Internat. Congress Mathematicians (Nice, 1970)'' , '''1''' , Gauthier-Villars (1971) pp. 425–430</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> P. Deligne (ed.) J.S. Milne (ed.) A. Ogus (ed.) K. Shih (ed.) , ''Hodge cycles, motives and Shimura varieties'' , ''Lect. notes in math.'' , '''900''' , Springer (1980)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> C. Soulé, "Groupes de Chow et <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m06504080.png" />-theory des variétés sur un corps fini" ''Math. Ann.'' , '''268''' (1984) pp. 317–345</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M. Rapoport (ed.) N. Schappacher (ed.) P. Schneider (ed.) , ''Beilinson's conjectures on special values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m06504081.png" />-functions'' , Acad. Press (1988)</TD></TR></table> | ||
Revision as of 08:01, 6 June 2020
A generalization of the various cohomology theories of algebraic varieties. The theory of motives systematically generalizes the idea of using the Jacobi variety of an algebraic curve $ X $
as a replacement for the cohomology group $ H ^ {1} ( X , \mathbf Q ) $
in the classical theory of correspondences, and the use of this theory in the study of the zeta-function of a curve $ X $
over a finite field. The theory of motives is universal in the sense that every geometric cohomology theory, of the type of the classical singular cohomology for algebraic varieties over $ \mathbf C $
with constant coefficients, every $ l $-
adic cohomology theory for various prime numbers $ l $
different from the characteristic of the ground field, every crystalline cohomology theory, etc. (see Weil cohomology) are functors on the category of motives.
Let $ V ( k) $ be the category of smooth projective varieties over a field $ k $ and let $ X \rightarrow C ( X) $ be a contravariant functor of global intersection theory from $ V ( k) $ into the category of commutative $ \Lambda $- algebras, where $ \Lambda $ is a fixed ring. For example, $ C ( X) $ is the Chow ring of classes of algebraic cycles (cf. Algebraic cycle) on $ X $ modulo a suitable (rational, algebraic, numerical, etc.) equivalence relation, or $ C ( X) = K ( X) $ is the Grothendieck ring, or $ C ( X) = H ^ {ev} ( X) $ is the ring of cohomology classes of even dimension, etc. The category $ V ( k) $ and the functor $ X \rightarrow C ( X) $ enable one to define a new category, the category of correspondences $ C V ( k) $, whose objects are varieties $ X \in V ( k) $, denoted by $ \overline{X}\; $, and whose morphisms are defined by the formula
$$ \mathop{\rm Hom} ( \overline{X}\; , \overline{Y}\; ) = C ( X \times Y ) $$
with the usual composition law for correspondences (see [1]). Let the functor $ C $ take values in the category of commutative graded $ \Lambda $- algebras $ A ( \Lambda ) $. Then $ C V ( k) $ will be the $ \Lambda $- additive category of graded correspondences. Moreover, $ C V ( k) $ will have direct sums and tensor products.
The category whose objects are the varieties from $ V ( k) $ and whose morphisms are correspondences of degree $ 0 $ is denoted by $ C V ^ {0} ( k) $. A natural functor from $ V ( k) $ into $ C V ^ {0} ( k) $ has been defined, and the functor $ C $ extends to a functor $ T $ from $ C V ^ {0} ( k) $ to $ A ( \Lambda ) $. The category $ C V ^ {0} ( k) $, like $ C V ( k) $, is not Abelian. Its pseudo-Abelian completion, the category $ M _ {C} ^ {+} ( k) $, has been considered. It is obtained from $ C V ^ {0} ( k) $ by the formal addition of the images of all projections $ p $. More precisely, the objects of $ M _ {C} ^ {+} ( k) $ are pairs $ ( \overline{X}\; , p ) $, where $ \overline{X}\; \in C V ^ {0} ( k) $ and $ p \in \mathop{\rm Hom} ( \overline{X}\; , \overline{X}\; ) $, $ p ^ {2} = p $, and $ H ( ( \overline{X}\; , p ) , ( \overline{Y}\; , q ) ) $ is the set of correspondences $ f : \overline{X}\; \rightarrow \overline{Y}\; $ such that $ f \circ p = = q \circ f $ modulo a correspondence $ g $ with $ g \circ p = p \circ g = 0 $. The category $ C V ^ {0} ( k) $ is imbedded in $ M _ {C} ^ {+} ( k) $ by means of the functor $ \overline{X}\; \rightarrow ( \overline{X}\; , \mathop{\rm id} ) $. The natural functor $ h : V ( k) \rightarrow M _ {C} ^ {+} ( k) $ is called the functor of motive cohomology spaces and $ M _ {C} ^ {+} ( k) $ is called the category of effective motives.
Let $ p = ( 1 \times e ) $, where $ e $ is the class of any rational point on the projective line $ P ^ {1} $, and let $ L = ( P ^ {1} , p ) $. Then
$$ h ( P ^ {n} ) = 1 \oplus L \oplus L ^ {\otimes _ {2} } \oplus \dots \oplus L ^ {\otimes _ {n} } . $$
If $ X = P ( E) $ is the projectivization of a locally free sheaf $ E $ of rank $ r $ on $ Y $, then
$$ h ( X) = \oplus _ {i = 0 } ^ { {r } - 1 } ( h ( Y) \otimes L ^ {\otimes _ {i} } ) . $$
Motives of a monodial transformation with a non-singular centre, motives of curves (see [1]), motives of Abelian manifolds (see [2]), and motives of Weil hypersurfaces have also been calculated.
The category of motives $ M _ {C} ( k) $ is obtained from $ M _ {C} ^ {+} ( k) $ by the formal addition of negative powers of the motives $ L $. By analogy with $ l $- adic cohomology, $ T = L ^ {\otimes _ {-} 1 } $ is called the Tate motive. Tensor multiplication with $ T $ is called twisting by the Tate motive. Twisting enables one to define the level of a motive as in an $ l $- adic cohomology theory. Any functor of the Weil cohomology factors through the functor $ h : V ( k) \rightarrow M _ {C} ( k) $. There is the conjecture that $ M _ {C} ( k) $ does not, in some sense, depend on the intersection theory of $ C $, and that the functor $ X \rightarrow h ( X) $ is itself a (universal) theory for the Weil cohomology. This conjecture is closely related to the standard Grothendieck conjectures (see [5]) on algebraic cycles (at present, 1982, not proved).
References
| [1] | Yu.I. Manin, "Correspondences, motives and monoidal transformations" Math. USSR Sb. , 6 : 4 (1968) pp. 439–470 Mat. Sb. , 77 : 4 (1968) pp. 475–507 |
| [2] | A.M. Shermenev, "The motif of an abelian variety" Uspekhi Mat. Nauk , 26 : 2 (1971) pp. 215–216 (In Russian) |
| [3] | M. Demazure, "Motives des variétés algébrique" , Sem. Bourbaki Exp. 365 , Lect. notes in math. , 180 , Springer (1971) pp. 19–38 |
| [4] | S.L. Kleiman, "Motives" P. Holm (ed.) , Algebraic Geom. Proc. 5-th Nordic Summer School Math. Oslo, 1970 , Wolters-Noordhoff (1972) pp. 53–96 |
| [5] | S.L. Kleiman, "Algebraic cycles and the Weil conjectures" A. Grothendieck (ed.) J. Giraud (ed.) et al. (ed.) , Dix exposés sur la cohomologie des schémas , North-Holland & Masson (1968) pp. 359–386 |
Comments
The theory of motives has been created by A. Grothendieck in the 1960-s. Although the above-mentioned standard conjectures on algebraic cycles have not yet (1989) been proved, the theory of motives has played an important role in various recent developments, for instance: i) as a guide for the Deligne–Hodge theory ([a1]); ii) in the study of absolute Hodge cycles on Abelian varieties ([a2]), where a variant of the notion of a motive has been used; iii) in the study of Chow groups on certain varieties over a finite field ([a3]); and iv) in work on the Beilinson's conjectures on special values of $ L $- functions (see [a4]).
References
| [a1] | P. Deligne, "Theory de Hodge I" , Proc. Internat. Congress Mathematicians (Nice, 1970) , 1 , Gauthier-Villars (1971) pp. 425–430 |
| [a2] | P. Deligne (ed.) J.S. Milne (ed.) A. Ogus (ed.) K. Shih (ed.) , Hodge cycles, motives and Shimura varieties , Lect. notes in math. , 900 , Springer (1980) |
| [a3] | C. Soulé, "Groupes de Chow et 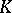 -theory des variétés sur un corps fini" Math. Ann. , 268 (1984) pp. 317–345 -theory des variétés sur un corps fini" Math. Ann. , 268 (1984) pp. 317–345 |
| [a4] | M. Rapoport (ed.) N. Schappacher (ed.) P. Schneider (ed.) , Beilinson's conjectures on special values of 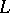 -functions , Acad. Press (1988) -functions , Acad. Press (1988) |
Motives, theory of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Motives,_theory_of&oldid=47909