Difference between revisions of "Krein space"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | k0558401.png | ||
| + | $#A+1 = 401 n = 3 | ||
| + | $#C+1 = 401 : ~/encyclopedia/old_files/data/K055/K.0505840 Kre\Auin space | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | Let $ {\mathcal K} $ | |
| + | be a complex linear space on a which a Hermitian sesquilinear form $ [ \cdot , \cdot ] $ | ||
| + | is defined (i.e. a mapping $ [ \cdot , \cdot ] : {\mathcal K} \times {\mathcal K} \rightarrow \mathbf C $ | ||
| + | such that $ [ \alpha _ {1} x _ {1} + \alpha _ {2} x _ {2} , y ] = \alpha _ {1} [ x _ {1} , y ] + \alpha _ {2} [ x _ {2} , y ] $ | ||
| + | and $ [ x , y ] = \overline{ {[ y , x ] }}\; $ | ||
| + | for all $ x _ {1} , x _ {2} , x , y \in {\mathcal K} $, | ||
| + | $ \alpha _ {1} , \alpha _ {2} \in \mathbf C $). | ||
| + | Then $ {\mathcal K} $( | ||
| + | or, more exactly, $ ( {\mathcal K} , [ \cdot , \cdot ] ) $) | ||
| + | is called a Krein space if in $ {\mathcal K} $ | ||
| + | there are two linear manifolds $ {\mathcal K} _ \pm $ | ||
| + | such that | ||
| + | |||
| + | $$ \tag{a1 } | ||
| + | {\mathcal K} = {\mathcal K} _ {+} \dot{+} {\mathcal K} _ {-} , | ||
| + | $$ | ||
| + | |||
| + | $ ( {\mathcal K} _ {+} , [ \cdot , \cdot ] ) $ | ||
| + | and $ ( {\mathcal K} _ {-} , - [ \cdot , \cdot ] ) $ | ||
| + | are Hilbert spaces (cf. [[Hilbert space|Hilbert space]]) and $ [ {\mathcal K} _ {+} , {\mathcal K} _ {-} ] = \{ 0 \} $. | ||
| + | It is always assumed that $ {\mathcal K} _ {+} , {\mathcal K} _ {-} \neq \{ 0 \} $( | ||
| + | otherwise $ ( {\mathcal K} , [ \cdot , \cdot ] ) $ | ||
| + | or $ ( {\mathcal K} , - [ \cdot , \cdot ] ) $ | ||
| + | is a Hilbert space); $ [ \cdot , \cdot ] $ | ||
| + | is called the indefinite inner product of the Krein space $ {\mathcal K} $. | ||
| + | If, in particular, $ \kappa = \min ( \mathop{\rm dim} {\mathcal K} _ {+} , \mathop{\rm dim} {\mathcal K} _ {-} ) < \infty $, | ||
| + | then $ {\mathcal K} _ {-} $ | ||
| + | is a $ \pi _ \kappa $- | ||
| + | space or Pontryagin space of index $ \kappa $( | ||
| + | cf. also [[Pontryagin space|Pontryagin space]]); in the sequel, for a $ \pi _ \kappa $- | ||
| + | space it is always assumed that $ \kappa = \mathop{\rm dim} {\mathcal K} _ {+} $. | ||
| − | Using the decomposition (a1), on the Krein space | + | Using the decomposition (a1), on the Krein space $ ( {\mathcal K} , [ \cdot , \cdot ] ) $ |
| + | a Hilbert inner product $ ( \cdot , \cdot ) $ | ||
| + | can be defined as follows: | ||
| − | + | $$ \tag{a2 } | |
| + | ( x , y ) = [ x _ {+} , y _ {+} ] - [ x _ {-} , y _ {-} ] , | ||
| + | $$ | ||
| − | + | $$ | |
| + | x = x _ {+} + x _ {-} ,\ y = y _ {+} + y _ {-} ,\ x _ \pm , y _ \pm \in {\mathcal K} _ {+} . | ||
| + | $$ | ||
| − | Although the decomposition (a1) is not unique, the decompositions of the components | + | Although the decomposition (a1) is not unique, the decompositions of the components $ {\mathcal K} _ \pm $ |
| + | are uniquely determined and the Hilbert norms, generated by different decompositions (a1) according to (a2), are equivalent. All topological notions in a Krein space, if not stated explicitly otherwise, refer to this topology. In the Hilbert space $ ( {\mathcal K} , ( \cdot , \cdot ) ) $, | ||
| + | the orthogonal projections onto $ {\mathcal K} _ {+} $ | ||
| + | and $ {\mathcal K} _ {-} $ | ||
| + | are denoted by $ P _ {+} $ | ||
| + | and $ P _ {-} $, | ||
| + | respectively. Then for the operator $ J = P _ {+} - P _ {-} $, | ||
| + | called a fundamental symmetry, one has | ||
| − | + | $$ \tag{a3 } | |
| + | [ x , y ] = ( J x , y ) ,\ \ | ||
| + | x , y \in {\mathcal K} , | ||
| + | $$ | ||
| − | and | + | and $ J $ |
| + | has the properties: $ J ^ {2} = I $, | ||
| + | $ J = J ^ {*} $. | ||
| + | Conversely, given a Hilbert space $ ( {\mathcal K} , ( \cdot , \cdot ) ) $ | ||
| + | and in it an operator $ J $ | ||
| + | with these properties (or, more generally, an operator $ G $ | ||
| + | with $ G = G ^ {*} $, | ||
| + | $ 0 \in \rho ( G) $), | ||
| + | then an indefinite inner product is defined on $ {\mathcal K} $ | ||
| + | by (a3) (or, respectively, by the relation | ||
| − | + | $$ \tag{a4 } | |
| + | [ x , y ] = ( G x , y ) ,\ \ | ||
| + | x , y \in {\mathcal K} \textrm{ ) } , | ||
| + | $$ | ||
| − | and | + | and $ ( {\mathcal K} , [ \cdot , \cdot ] ) $ |
| + | is a Krein space. Because of this construction, Krein spaces are sometimes called $ J $- | ||
| + | spaces. | ||
| − | If, more generally, a Hilbert space | + | If, more generally, a Hilbert space $ ( {\mathcal H} , ( \cdot , \cdot ) ) $ |
| + | and a bounded self-adjoint, not semi-definite, operator $ G $ | ||
| + | in $ {\mathcal H} $ | ||
| + | are given, the relation (a4) with $ x , y \in {\mathcal H} $ | ||
| + | defines a Hermitian sesquilinear form $ [ \cdot , \cdot ] $ | ||
| + | on $ {\mathcal H} $. | ||
| + | This form can be extended by continuity to the completion of the quotient space $ {\mathcal H} / \mathop{\rm Ker} G $ | ||
| + | with respect to the norm $ \| | G | ^ {1/2} x \| $( | ||
| + | $ x \in {\mathcal H} $). | ||
| + | This completion, equipped with $ [ \cdot , \cdot ] $, | ||
| + | is a Krein space containing $ {\mathcal H} / \mathop{\rm Ker} G $ | ||
| + | as a dense subset. | ||
| − | If | + | If $ r $ |
| + | is a real and locally summable function on $ \mathbf R $ | ||
| + | which assumes positive and negative values on sets of positive [[Lebesgue measure|Lebesgue measure]], then the space $ L _ {2,r} $ | ||
| + | of all (classes of) measurable functions (cf. [[Measurable function|Measurable function]]) $ f $ | ||
| + | on $ \mathbf R $ | ||
| + | such that $ \int _ {- \infty } ^ \infty | f | ^ {2} | r | d x < \infty $ | ||
| + | and equipped with the indefinite inner product $ [ f , g ] = \int _ {- \infty } ^ \infty f \overline{g}\; r d x $( | ||
| + | $ f , g \in L _ {2,r} $) | ||
| + | is a Krein space. More generally, if $ \sigma $ | ||
| + | is a real function which is locally of bounded variation and not isotone on $ \mathbf R $ | ||
| + | and $ | \sigma | $ | ||
| + | denotes its total variation, then the space $ L _ {2} ( \sigma ) $, | ||
| + | of all measurable functions $ f $ | ||
| + | such that $ \int _ {- \infty } ^ \infty | f | ^ {2} d | \sigma | < \infty $ | ||
| + | and equipped with the indefinite inner product $ [ f , g ] = \int _ {- \infty } ^ {- \infty } f \overline{g}\; d \sigma $( | ||
| + | $ f , g \in L _ {2} ( \sigma ) $) | ||
| + | is a Krein space. | ||
| − | Further, a complex linear space with a Hermitian sesquilinear form | + | Further, a complex linear space with a Hermitian sesquilinear form $ [ \cdot , \cdot ] $, |
| + | which has $ \kappa $ | ||
| + | negative squares (that is, each linear manifold $ {\mathcal L} \subset {\mathcal K} $ | ||
| + | with $ [ x , x ] < 0 $ | ||
| + | for $ x \in {\mathcal L} $, | ||
| + | $ x \neq 0 $, | ||
| + | is of dimension $ \leq \kappa $ | ||
| + | and at least one such manifold is of dimension $ \kappa $), | ||
| + | can be canonically imbedded into a $ \pi _ \kappa $- | ||
| + | space by taking a quotient space and completing it (see [[#References|[a4]]], [[#References|[a2]]], [[#References|[a9]]], [[#References|[a11]]]). | ||
| − | The indefinite inner product | + | The indefinite inner product $ [ \cdot , \cdot ] $ |
| + | on the Krein space $ {\mathcal K} $ | ||
| + | gives rise to a classification of the elements of $ {\mathcal K} $: | ||
| + | $ x \in {\mathcal K} $ | ||
| + | is called positive, non-negative, neutral, etc. if $ [ x , x ] > 0 $, | ||
| + | $ [ x , x ] < 0 $, | ||
| + | $ [ x , x ] = 0 $, | ||
| + | etc. A linear manifold or a subspace $ {\mathcal L} $ | ||
| + | in $ {\mathcal K} $ | ||
| + | is called positive, non-negative, neutral, etc. if all its non-zero elements are positive, non-negative, neutral, etc. The set of all, e.g., non-negative elements is not linear, but it contains subspaces, and among them maximal ones, called maximal non-negative subspaces. All maximal non-negative subspaces of the Krein space $ {\mathcal K} $ | ||
| + | have the same dimension (as $ {\mathcal K} _ {+} $). | ||
| + | A subspace $ {\mathcal L} $ | ||
| + | of $ {\mathcal K} $( | ||
| + | with the decomposition (a1)) is maximal non-negative if and only if it can be written as $ {\mathcal L} = \{ {x _ {+} + K _ {\mathcal L} x _ {+} } : {x _ {+} \in {\mathcal K} _ {+} } \} $, | ||
| + | where $ K _ {\mathcal L} $, | ||
| + | the angular operator of $ {\mathcal L} $, | ||
| + | is a [[Contraction(2)|contraction]] from $ ( {\mathcal K} _ {+} , [ \cdot , \cdot ] ) $ | ||
| + | into $ ( {\mathcal K} _ {-} , [ \cdot , \cdot ] ) $. | ||
| + | A dual pair $ ( {\mathcal L} _ {+} , {\mathcal L} _ {-} ) $ | ||
| + | of subspaces of $ {\mathcal K} $ | ||
| + | is defined as follows: $ {\mathcal L} _ {+} $ | ||
| + | is a non-negative subspace, $ {\mathcal L} _ {-} $ | ||
| + | is a non-positive subspace and $ [ {\mathcal L} _ {+} , {\mathcal L} _ {-} ] = \{ 0 \} $. | ||
| + | Any dual pairs is contained in a maximal dual pair (maximality of dual pairs is defined in a natural way by inclusion); in a maximal dual pair $ ( {\mathcal L} _ {+} , {\mathcal L} _ {-} ) $ | ||
| + | the subspace $ {\mathcal L} _ {+} $( | ||
| + | respectively, $ {\mathcal L} _ {-} $) | ||
| + | is maximal non-negative (respectively, non-positive) (R.S. Phillips). | ||
| − | Using the indefinite inner product, orthogonality can be defined in | + | Using the indefinite inner product, orthogonality can be defined in $ {\mathcal K} $: |
| + | $ x , y \in {\mathcal K} $ | ||
| + | are called orthogonal if $ [ x , y ] = 0 $; | ||
| + | if $ {\mathcal L} \subset {\mathcal K} $, | ||
| + | then $ {\mathcal L} ^ \perp = \{ {x } : {[ x , {\mathcal L} ] = \{ 0 \} } \} $. | ||
| + | Some properties of orthogonality in a Hilbert space are preserved; however, there are also essential differences; e.g., $ {\mathcal L} \cap {\mathcal L} ^ \perp $ | ||
| + | can contain non-zero vectors; $ {\mathcal L} \cap {\mathcal L} ^ \perp $ | ||
| + | coincides with $ {\mathcal L} $ | ||
| + | if $ {\mathcal L} $ | ||
| + | is neutral, and $ {\mathcal L} \cap {\mathcal L} ^ \perp = \{ 0 \} $ | ||
| + | is equivalent to $ \overline{ {{\mathcal L} + {\mathcal L} ^ \perp }}\; = {\mathcal K} $. | ||
| − | For a densely-defined [[Linear operator|linear operator]] | + | For a densely-defined [[Linear operator|linear operator]] $ T $ |
| + | in the Krein space $ ( {\mathcal K} , [ \cdot , \cdot ] ) $ | ||
| + | an adjoint $ T ^ { + } $( | ||
| + | sometimes called $ J $- | ||
| + | adjoint) is defined by $ [ T x , y ] = [ x , T ^ { + } y ] $( | ||
| + | $ x \in {\mathcal D} ( T) $, | ||
| + | $ y \in {\mathcal D} ( T ^ { + } ) $). | ||
| + | If $ T ^ { * } $ | ||
| + | denotes the adjoint of $ T $ | ||
| + | in the Hilbert space $ ( {\mathcal K} , ( \cdot , \cdot ) ) $( | ||
| + | see (a2)), then evidently $ T ^ { + } = J T ^ { * } J $. | ||
| + | Now in the Krein space $ {\mathcal K} $ | ||
| + | classes of operators are defined more or less similarly to the case of a Hilbert space: $ T $ | ||
| + | is symmetric if $ T \subset T ^ { + } $, | ||
| + | self-adjoint if $ T = T ^ { + } $, | ||
| + | dissipative if $ \mathop{\rm Im} [ T x , x ] \geq 0 $( | ||
| + | $ x \in {\mathcal D} ( T) $), | ||
| + | contractive if $ [ T x , T x ] \leq [ x , x ] $( | ||
| + | $ x \in {\mathcal K} $), | ||
| + | unitary if $ T $ | ||
| + | is bounded, $ {\mathcal D} ( T) = {\mathcal K} $ | ||
| + | and $ T ^ { + } T = I = T T ^ { + } $, | ||
| + | etc. Also, new classes of operators arise: E.g., $ T $ | ||
| + | is a plus-operator if $ [ x , x ] \geq 0 $ | ||
| + | implies $ [ T x , T x ] \geq 0 $, | ||
| + | and a doubly plus-operator if $ T $ | ||
| + | and $ T ^ { + } $ | ||
| + | are plus-operators. In a Krein space a densely-defined [[Isometric operator|isometric operator]] $ T $( | ||
| + | i.e. $ [ T x , T y ] = [ x , y ] $ | ||
| + | for all $ x , y \in {\mathcal D} ( T) $) | ||
| + | need not be continuous. As in a Hilbert space, self-adjoint and unitary, symmetric and isometric, dissipative and contractive operators are related by the [[Cayley transform|Cayley transform]]. E.g., if $ A = A ^ {+} $, | ||
| + | $ z _ {0} \neq \overline{z}\; _ {0} $ | ||
| + | and $ z _ {0} \in \rho ( A) $, | ||
| + | then $ U = ( A - \overline{z}\; _ {0} ) ( A - z _ {0} ) ^ {-} 1 $ | ||
| + | is unitary. | ||
| − | The spectrum of a self-adjoint operator | + | The spectrum of a self-adjoint operator $ A $ |
| + | in a Krein space is not necessarily real (it can even cover the whole plane), but it is symmetric with respect to the real axis. Similarly, the spectrum of a unitary operator is symmetric with respect to the unit circle. | ||
The indefinite inner product sometimes gives a classification of the points of the spectrum of an operator: An eigen value is said to be of positive type (negative type, etc.) if the corresponding eigen space is positive (negative, etc.). | The indefinite inner product sometimes gives a classification of the points of the spectrum of an operator: An eigen value is said to be of positive type (negative type, etc.) if the corresponding eigen space is positive (negative, etc.). | ||
| − | If | + | If $ \lambda $, |
| + | $ \overline \lambda \; $ | ||
| + | are isolated eigen values of the self-adjoint operator $ A $ | ||
| + | in a Krein space, then for the corresponding Riesz projections $ E _ \lambda $, | ||
| + | $ E _ {\overline \lambda \; } $ | ||
| + | one has $ E _ {\overline \lambda \; } = E _ \lambda ^ {+} $, | ||
| + | and if, e.g., $ \mathop{\rm dim} {\mathcal R} ( E _ \lambda ) < \infty $, | ||
| + | then the restrictions $ A \mid _ { {\mathcal R} ( E _ \lambda ) } $ | ||
| + | and $ A \mid _ { {\mathcal R} ( E _ {\overline \lambda \; } ) } $ | ||
| + | have the same Jordan structure. If in a $ \pi _ \kappa $- | ||
| + | space the symmetric operator $ A $ | ||
| + | has a real non-semi-simple eigen value $ \lambda $, | ||
| + | then the corresponding algebraic eigen space $ {\mathcal E} _ \lambda $ | ||
| + | can be decomposed into a direct orthogonal sum: $ {\mathcal E} _ \lambda = {\mathcal E} _ \lambda ^ { \prime } + {\mathcal E} _ \lambda ^ { \prime\prime } $, | ||
| + | where $ {\mathcal E} _ \lambda ^ { \prime\prime } $ | ||
| + | is a positive subspace contained in the geometric eigen space of $ A $ | ||
| + | at $ \lambda $, | ||
| + | and $ {\mathcal E} _ \lambda ^ { \prime } \neq \{ 0 \} $ | ||
| + | is invariant under $ A $ | ||
| + | with $ \mathop{\rm dim} {\mathcal E} _ \lambda ^ { \prime } < \infty $; | ||
| + | if $ d _ {1} \dots d _ {r} $ | ||
| + | are the lengths of the Jordan chains of $ A \mid _ { {\mathcal E} _ \lambda ^ { \prime } } $, | ||
| + | one puts $ \rho ( \lambda )= \sum _ {j=} 1 ^ \kappa [ d _ {j} /2 ] $; | ||
| + | if $ \lambda $ | ||
| + | is a non-real eigen value of $ A $, | ||
| + | one defines $ \rho ( \lambda ) $ | ||
| + | as the dimension of the corresponding algebraic eigen space. Then $ \sum \rho ( \lambda ) \leq \kappa $, | ||
| + | where the sum extends over all eigen values $ \lambda $ | ||
| + | of $ A $ | ||
| + | in the closed upper half-plane. In particular, the length of any Jordan chain of $ A $ | ||
| + | is $ \leq 2 \kappa + 1 $, | ||
| + | and the number of eigen values of $ A $ | ||
| + | in the open upper half-plane, and also the number of non-semi-simple eigen values of $ A $, | ||
| + | does not exceed $ \kappa $. | ||
| − | Specific results for Krein spaces are statements about the existence of maximal non-negative (or maximal non-positive) subspaces, which are invariant under a given operator. The first general result of this type was proved by L.S. Pontryagin in 1944, stating that a self-adjoint operator in a | + | Specific results for Krein spaces are statements about the existence of maximal non-negative (or maximal non-positive) subspaces, which are invariant under a given operator. The first general result of this type was proved by L.S. Pontryagin in 1944, stating that a self-adjoint operator in a $ \pi _ \kappa $- |
| + | space has a $ \kappa $- | ||
| + | dimensional non-positive (that is, a maximal non-positive) invariant subspace. Subsequently, similar results were proved for various classes of operators in Krein spaces. E.g., a bounded linear operator $ T $ | ||
| + | in a Krein space has a maximal non-negative invariant subspace if $ P _ {+} T P _ {-} $ | ||
| + | is compact and, additionally, $ T $ | ||
| + | is self-adjoint or dissipative or unitary or a plus-operator, etc. (see [[#References|[a2]]], [[#References|[a4]]]). One possibility for proving these results, e.g. for a unitary operator $ T $, | ||
| + | is to establish the existence of a fixed point $ K _ {0} $ | ||
| + | of the fractional-linear transformation | ||
| − | + | $$ | |
| + | K \rightarrow ( T _ {21} + T _ {22} K ) ( T _ {11} + T _ {12} K ) ^ {-} 1 , | ||
| + | $$ | ||
| − | where | + | where $ K $ |
| + | is a contraction from $ {\mathcal K} _ {+} $ | ||
| + | into $ {\mathcal K} _ {-} $( | ||
| + | an angular operator) and $ ( T _ {ij} ) _ {1} ^ {2} $ | ||
| + | is the matrix representation of $ T $ | ||
| + | with respect to (a1). By different methods also in other cases the existence of a maximal non-negative invariant subspace has been proved, e.g.: 1) $ T $ | ||
| + | is unitary and $ \| T ^ { n } \| $ | ||
| + | is uniformly bounded for all $ n = 0 , 1 ,\dots $; | ||
| + | 2) $ [ T x , T x ] > [ x , x ] $ | ||
| + | for all $ x \in {\mathcal K} $, | ||
| + | $ x \neq 0 $, | ||
| + | and $ \sigma ( T) \cap \{ | \rho | = 1 \} = \emptyset $; | ||
| + | and 3) $ T $ | ||
| + | is bounded, self-adjoint and there exists a polynomial $ p $ | ||
| + | such that $ [ p ( T) x , x ] \geq 0 $( | ||
| + | $ x \in {\mathcal K} $). | ||
| + | In many cases these maximal non-positive invariant subspaces $ {\mathcal L} $ | ||
| + | can be specified by properties of the spectrum of $ A \mid _ {\mathcal L} $. | ||
| + | E.g., if $ T $ | ||
| + | is bounded, self-adjoint and $ P _ {+} T P _ {-} $ | ||
| + | is compact, then $ {\mathcal L} $ | ||
| + | can be chosen such that $ \mathop{\rm Im} \sigma ( A \mid _ {\mathcal L} ) \geq 0 $. | ||
| + | There are also results about the existence of a common invariant maximal non-positive subspace for a commuting family of operators, e.g.: A commuting family of bounded self-adjoint operators in a $ \pi _ \kappa $- | ||
| + | space has a common maximal non-negative invariant subspace (M.A. Naimark; for applications in the representation theory of groups in $ \pi _ \kappa $- | ||
| + | spaces see [[#References|[a19]]]). Phillips asked ([[#References|[a16]]]) if a dual pair of subspaces of $ {\mathcal K} $ | ||
| + | which are invariant under a commutative algebra $ A $ | ||
| + | of bounded self-adjoint operators in the Krein space $ {\mathcal K} $ | ||
| + | can always be extended to a maximal dual pair whose subspaces are still invariant under $ A $( | ||
| + | which would imply that each bounded self-adjoint operator in $ {\mathcal K} $ | ||
| + | has a maximal non-negative invariant subspace). Only partial solutions to this problem are known (cf. [[#References|[a4]]], [[#References|[a2]]], [[#References|[a14]]]). | ||
| − | A self-adjoint operator | + | A self-adjoint operator $ A $ |
| + | in the Krein space $ {\mathcal K} $ | ||
| + | is called definitizable (positizable in [[#References|[a4]]]) if $ \rho ( A) \neq \emptyset $ | ||
| + | and if there exists a polynomial $ p $ | ||
| + | such that $ [ p ( A) x , x ] \geq 0 $( | ||
| + | $ x \in {\mathcal D} ( p ( A) ) $). | ||
| + | Each self-adjoint operator $ A $ | ||
| + | in a $ \pi _ \kappa $- | ||
| + | space has this property (where $ p $ | ||
| + | can be chosen to be $ q \overline{q}\; $ | ||
| + | with $ q $ | ||
| + | the minimal polynomial of $ A \mid _ {\mathcal L} $, | ||
| + | $ {\mathcal L} $ | ||
| + | being a $ \kappa $- | ||
| + | dimensional non-positive invariant subspace of $ A $); | ||
| + | also, each self-adjoint operator $ A $ | ||
| + | in a Krein space for which $ \rho ( A ) \neq \emptyset $ | ||
| + | and for which the Hermitian sesquilinear form $ [ A x , y ] $( | ||
| + | $ x , y \in {\mathcal D} ( A) $) | ||
| + | has a finite number of negative squares, is definitizable. | ||
| − | The non-real spectrum | + | The non-real spectrum $ \sigma _ {0} ( A) $ |
| + | of the definitizable operator $ A $ | ||
| + | consists of at most finitely many eigen values, and $ A $ | ||
| + | has a [[Spectral function|spectral function]], with possibly certain critical points [[#References|[a13]]], [[#References|[a2]]]. This means that there is a finite set $ c ( A) \subset \mathbf R \cup \{ \infty \} $( | ||
| + | of critical points) such that on the semi-ring $ \mathbf R _ {A} $, | ||
| + | consisting of all bounded intervals of $ \mathbf R $ | ||
| + | with end points not in $ c ( A) $ | ||
| + | and their complements, a homomorphism $ E $ | ||
| + | with values in the set of all self-adjoint projections in the Krein space $ {\mathcal K} $ | ||
| + | is defined, such that for $ \Delta \in \mathbf R _ {A} $: | ||
| + | a) $ E ( \Delta ) {\mathcal K} $ | ||
| + | is a positive (negative) subspace if $ p > 0 $( | ||
| + | respectively, $ p < 0 $) | ||
| + | on $ \overline \Delta \; \cap \sigma ( A) $ | ||
| + | for some definitizing polynomial $ p $ | ||
| + | of $ A $; | ||
| + | b) $ E ( \Delta ) $ | ||
| + | is in the double commutant of the [[Resolvent|resolvent]] of $ A $; | ||
| + | and c) if $ \Delta $ | ||
| + | is bounded, then $ E ( \Delta ) {\mathcal K} \subset {\mathcal D} ( A) $ | ||
| + | and $ \sigma ( A \mid _ {E ( \Delta ) {\mathcal K} } ) \subset \overline \Delta \; $, | ||
| + | $ \sigma ( A \mid _ {( I - E ( \Delta ) ) {\mathcal K} } ) \subset \overline{ {( \mathbf R \setminus \Delta ) }}\; \cup \sigma _ {0} ( A) $. | ||
| + | If, in particular, $ A $ | ||
| + | is bounded and $ [ A x , x ] \geq 0 $( | ||
| + | $ x \in {\mathcal K} $), | ||
| + | then $ c ( A) \subset \{ 0 \} $, | ||
| + | and one has | ||
| − | + | $$ | |
| + | A x = \int\limits _ {- \| A \| } ^ { {\| } A \| } \lambda E ( d \lambda ) x + N x , | ||
| + | $$ | ||
| − | for some bounded operator | + | for some bounded operator $ N $ |
| + | such that $ N = N ^ {+} $, | ||
| + | $ N ^ {2} = 0 $, | ||
| + | $ [ N x , x ] \geq 0 $( | ||
| + | $ x \in {\mathcal K} $). | ||
| − | If the spectrum of a definitizable operator | + | If the spectrum of a definitizable operator $ A $ |
| + | is discrete, then the linear span of its algebraic eigen spaces is dense in $ {\mathcal K} $; | ||
| + | if $ A $ | ||
| + | is compact and self-adjoint in a $ \pi _ \kappa $- | ||
| + | space $ {\mathcal K} $ | ||
| + | and $ 0 \notin \sigma _ {p} ( A) $, | ||
| + | then there is a [[Riesz basis|Riesz basis]] of $ {\mathcal K} $ | ||
| + | consisting of eigen and associated vectors of $ A $( | ||
| + | I.S. Iokhvidov). | ||
| − | There is a theory of extensions of symmetric operators to self-adjoint operators and of generalized resolvents in | + | There is a theory of extensions of symmetric operators to self-adjoint operators and of generalized resolvents in $ \pi _ \kappa $- |
| + | spaces, and also in Krein spaces, which is similar to the Hilbert space situation. The same is true for dilation theory: Each bounded linear operator $ T $ | ||
| + | in a Krein space $ {\mathcal K} $ | ||
| + | has a unitary dilation $ T $ | ||
| + | in some Krein space $ {\mathcal K} tilde \supset {\mathcal K} $([[#References|[a2]]]). In this context one has the following result: Let $ {\mathcal K} _ {1} $, | ||
| + | $ {\mathcal K} _ {2} $ | ||
| + | be Krein spaces, $ {\mathcal D} $ | ||
| + | a simply-connected open domain with smooth boundary such that $ 0 \in {\mathcal D} $, | ||
| + | $ \overline{ {\mathcal D} }\; \subset \{ {z } : {| z | < 1 } \} $, | ||
| + | and let $ \Theta $ | ||
| + | be a function which is holomorphic in $ {\mathcal D} $ | ||
| + | whose values are bounded linear operators from $ {\mathcal K} _ {1} $ | ||
| + | to $ {\mathcal K} _ {2} $. | ||
| + | Then there exists a Krein space $ {\mathcal K} $ | ||
| + | and a unitary operator | ||
| − | + | $$ | |
| + | U = \left ( | ||
| + | \begin{array}{ll} | ||
| + | U _ {11} &U _ {12} \\ | ||
| + | U _ {21} &U _ {22} \\ | ||
| + | \end{array} | ||
| + | \right ) : {\mathcal K} \oplus {\mathcal K} _ {1} \rightarrow {\mathcal K} \oplus {\mathcal K} _ {2} , | ||
| + | $$ | ||
such that | such that | ||
| − | + | $$ | |
| + | \Theta ( z) = U _ {22} + z U _ {21} ( I - z U _ {11} ) ^ {-} 1 U _ {12} \ \ | ||
| + | ( z \in {\mathcal D} ) | ||
| + | $$ | ||
| + | |||
| + | (T.Ya. Azizov, see [[#References|[a2]]], [[#References|[a6]]]; here unitary means that $ U $ | ||
| + | maps the Krein space $ {\mathcal K} \oplus {\mathcal K} _ {1} $ | ||
| + | continuously onto the Krein space $ {\mathcal K} \oplus {\mathcal K} _ {2} $, | ||
| + | preserving the indefinite inner product). | ||
| − | ( | + | Some of the first papers about Krein spaces or, more generally, spaces with indefinite inner product, were stimulated by problems of (quantum) mechanics ([[#References|[a4]]], [[#References|[a2]]]; see also [[#References|[a18]]], [[#References|[a17]]]). Operators in Krein spaces arise also in a natural way in problems in mathematical analysis. Some examples of these are: I) Consider the canonical system of differential equations $ J \dot{x} ( t) = i H ( t) x ( t) $ |
| + | on $ [ 0 , \infty ) $, | ||
| + | where $ H ( t) $, | ||
| + | $ J $ | ||
| + | are $ ( n \times n ) $ | ||
| + | matrices, $ H ( t ) \geq 0 $, | ||
| + | $ J = J ^ {*} = J ^ {-} 1 $, | ||
| + | and let $ U ( t) $ | ||
| + | be the corresponding matrizant (cf. [[Cauchy operator|Cauchy operator]]): $ J \dot{U} ( t) = i H ( t) U ( t) $, | ||
| + | $ U ( 0) = I _ {n} $. | ||
| + | Then $ U ( t) $ | ||
| + | is $ J $- | ||
| + | unitary (that is, unitary with respect to the inner product defined in $ \mathbf C ^ {n} $ | ||
| + | by the matrix $ J $, | ||
| + | see (a3)), and, e.g., in the stability theory for periodic equations $ ( H ( t) = H ( T + t ) ) $ | ||
| + | the classification of the eigen values of $ U ( T) $ | ||
| + | into those of positive or negative type plays an essential role ([[#References|[a5]]], [[#References|[a8]]]). II) The integral operator $ x ( \cdot ) \rightarrow \int _ {a} ^ {b} K ( \cdot , s ) x ( s ) d \sigma ( s) $, | ||
| + | $ \sigma $ | ||
| + | real and of bounded variation on the interval $ [ a , b ] $, | ||
| + | $ K ( s , t ) = \overline{ {K ( t , s ) }}\; $( | ||
| + | $ s , t \in [ a , b ] $), | ||
| + | is self-adjoint in the Krein space $ L _ {2} ( \sigma ) $. | ||
| + | III) The theory of dual pairs of subspaces of a Krein space and their extensions to maximal dual pairs is related to certain questions in the theory of extensions of dissipative operators in a Hilbert space to maximal dissipative ones. Phillips started these investigations in connection with the Cauchy problem for dissipative hyperbolic and parabolic systems (see [[#References|[a2]]], [[#References|[a4]]] for references). IV) With the monic operator polynomial $ L ( \lambda ) = \lambda ^ {n} I + \lambda ^ {n-} 1 B _ {n-} 1 + \dots + \lambda B _ {1} + B _ {0} $, | ||
| + | $ B _ {j} $ | ||
| + | bounded self-adjoint operators in some Hilbert space $ {\mathcal H} $, | ||
| + | one can associate the so-called companion operator | ||
| − | + | $$ | |
| + | A = \left ( | ||
| + | \begin{array}{ccccc} | ||
| + | - B _ {n-} 1 &- B _ {n-} 2 &\dots &- B _ {1} &- B _ {0} \\ | ||
| + | I & 0 &\dots & 0 & 0 \\ | ||
| + | \cdot &\cdot &\dots &\cdot &\cdot \\ | ||
| + | 0 & 0 &\dots & I & 0 \\ | ||
| + | \end{array} | ||
| + | \right ) , | ||
| + | $$ | ||
| − | + | which is self-adjoint in the Krein space $ {\mathcal K} = {\mathcal H} ^ {n} $, | |
| + | $ [ x , y ] = ( G x , y ) $( | ||
| + | $ x , y \in {\mathcal H} ^ {n} $), | ||
| + | where $ ( \cdot , \cdot ) $ | ||
| + | is the inner product in $ {\mathcal H} ^ {n} $ | ||
| + | and | ||
| − | + | $$ | |
| + | G = \left ( | ||
| + | \begin{array}{cccc} | ||
| + | 0 & 0 &\dots & I \\ | ||
| + | 0 & 0 &{} &B _ {n-} 1 \\ | ||
| + | \cdot &\cdot &{} &\cdot \\ | ||
| + | \cdot &\cdot &{} &\cdot \\ | ||
| + | \cdot &\cdot &{} &\cdot \\ | ||
| + | I &B _ {n-} 1 &\dots &B _ {1} \\ | ||
| + | \end{array} | ||
| + | \right ) . | ||
| + | $$ | ||
| − | + | If, e.g., $ n = 2 $ | |
| + | and $ B _ {0} $ | ||
| + | is compact and $ \geq 0 $, | ||
| + | the results about the existence of maximal non-negative invariant subspaces mentioned above imply that there exists a bounded linear operator $ Z $ | ||
| + | in $ {\mathcal H} $ | ||
| + | satisfying $ Z ^ {2} + B _ {1} Z + B _ {0} = 0 $, | ||
| + | $ Z ^ {*} Z \leq B _ {0} $ | ||
| + | and $ \mathop{\rm Im} \sigma ( Z) \geq 0 $[[#References|[a12]]]. In a similar way, if $ B \geq 0 $, | ||
| + | $ C = C ^ {*} $ | ||
| + | and $ A $ | ||
| + | are $ ( n \times n ) $ | ||
| + | matrices such that $ G = ( _ { A } ^ {-} C {} _ {B} ^ {A ^ {*} } ) $ | ||
| + | has $ n $ | ||
| + | positive and $ n $ | ||
| + | negative eigen values, the solutions $ X $ | ||
| + | of the matrix [[Riccati equation|Riccati equation]] | ||
| − | + | $$ | |
| + | X B X + X A + A ^ {*} X - C = 0 | ||
| + | $$ | ||
| − | + | with $ ( X ^ {*} - X ) ( A + B X ) \geq 0 $ | |
| + | are in bijective correspondence with all maximal non-positive subspaces which are invariant under the self-adjoint operator $ T = i ( _ {C} ^ {A} {} _ {- A ^ {*} } ^ { B } ) $ | ||
| + | in the $ 2n $- | ||
| + | dimensional Krein space $ {\mathcal K} = \mathbf C ^ {2n} $, | ||
| + | equipped with the indefinite inner product (a4) (see [[#References|[a8]]]). V) If $ L $ | ||
| + | is a formally-symmetric regular ordinary differential operator on the interval $ [ a , b ] $ | ||
| + | with symmetric boundary conditions at $ a $ | ||
| + | and $ b $, | ||
| + | and $ r $ | ||
| + | is a summable function on $ [ a , b ] $ | ||
| + | which is not of constant sign (a.e.) on $ [ a , b ] $, | ||
| + | then the differential equation $ L y - \lambda r y = r f $ | ||
| + | leads to a self-adjoint operator $ A $ | ||
| + | in the Krein space $ {\mathcal K} = L _ {2,r} $ | ||
| + | with inner product $ [ f , g ] = \int _ {a} ^ {b} f \overline{g}\; r d x $. | ||
| + | If $ L $ | ||
| + | is semi-bounded from below, the operator $ A $ | ||
| + | is definitizable. VI) Krein spaces can be associated with certain eigen value problems for ordinary differential operators containing the eigen value parameters in the boundary conditions. E.g., consider in $ L _ {2} = L _ {2} [ 0 , \infty ) $ | ||
| + | the problem | ||
| − | + | $$ | |
| + | - | ||
| + | \frac{d ^ {2} y }{d x ^ {2} } | ||
| + | + | ||
| + | q y - \lambda y = f , | ||
| + | $$ | ||
| − | + | which is supposed to have a limit point at $ \infty $ | |
| + | and with a boundary condition $ \alpha ( \lambda ) y ( 0) + \beta ( \lambda ) y ^ \prime ( 0) = 0 $ | ||
| + | at $ x = 0 $( | ||
| + | $ \alpha $, | ||
| + | $ \beta $ | ||
| + | are functions which are holomorphic on some set $ D _ {\alpha , \beta } \subset \mathbf C $ | ||
| + | and satisfying a symmetry condition). The solution of this problem can be represented as $ y = P ( A - \lambda I ) ^ {-} 1 f $( | ||
| + | $ f \in L _ {2} $), | ||
| + | where, in general, $ A $ | ||
| + | is a self-adjoint operator in some Krein space $ {\mathcal K} = L _ {2} \oplus {\mathcal K} _ {1} $ | ||
| + | and $ P $ | ||
| + | is the orthogonal projection from $ {\mathcal K} $ | ||
| + | onto $ L _ {2} $[[#References|[a17]]]. VII) Certain classes of analytic functions are closely related to the theory of operators in $ \pi _ \kappa $- | ||
| + | spaces. This concerns, e.g., functions $ f $ | ||
| + | which are defined and meromorphic in the upper half-plane (or the unit disc) and which are such that the kernel | ||
| − | + | $$ | |
| + | N _ {f} ( z , \rho ) = \ | ||
| − | + | \frac{f ( z) - \overline{ {f ( \rho ) }}\; }{z - \overline \rho \; } | |
| + | |||
| + | $$ | ||
(or | (or | ||
| − | + | $$ | |
| + | \left . S _ {f} ( z , \overline \rho \; ) = \ | ||
| + | |||
| + | \frac{1 - f ( z) \overline{ {f ( \rho ) }}\; }{1 - z \overline \rho \; } | ||
| + | \right ) | ||
| + | $$ | ||
| − | has | + | has $ \kappa $ |
| + | negative squares (that is, for arbitrary $ n $ | ||
| + | and $ z _ {1} \dots z _ {n} $, | ||
| + | the matrix $ ( N _ {f} ( z _ {i} , z _ {j} ) ) _ {1} ^ {n} $ | ||
| + | has at most $ n $ | ||
| + | negative eigen values and for at least one choice of $ n , z _ {1} \dots z _ {n} $ | ||
| + | it has $ \kappa $ | ||
| + | negative eigen values). Corresponding extrapolation or moment problems can be treated by making use of results of the theory of symmetric or isometric operators in $ \pi _ \kappa $- | ||
| + | spaces (see [[#References|[a12]]], [[#References|[a2]]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> T.Ya Azizov, I.S. Iokhvidov, "Linear operators in spaces with indefinite metric and their applications" ''Russian Math. Surveys'' , '''15''' (1981) pp. 438–490 ''Itogi Nauk. i Tekhn. Mat. Anal.'' , '''17''' (1979) pp. 113–205</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> T.Ya Azizov, I.S. Iokhvidov, "Foundations of the theory of linear operators in spaces with indefinite metric" , Moscow (1986) (In Russian)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> T. Ando, "Linear operators in Krein spaces" , Hokkaido Univ. (1979)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> J. Bognár, "Indefinite inner product spaces" , Springer (1974)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> Yu.L. Daletskii, M.G. Krein, "Stability of solutions of differential equations in Banach space" , Amer. Math. Soc. (1974) (Translated from Russian)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> A. Dijksma, H. Langer, H.S.V. de Snoo, "Unitary colligations in Krein spaces and their role in the extension theory of isometries and symmetric linear relations in Hilbert spaces" S. Kurepa (ed.) et al. (ed.) , ''Foundational analysis II'' , ''Lect. notes in math.'' , '''1247''' , Springer (1987) pp. 1–42</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> A. Dijksma, H. Langer, H.S.V. de Snoo, "Symmetric Sturm–Liouville operators with eigenvalues depending boundary conditions" , ''Oscillation, Bifurcations and Chaos'' , ''CMS Conf. Proc.'' , '''8''' , Amer. Math. Soc. (1987) pp. 87–116</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> I. [I. Gokhberg] Gohberg, P. Lancaster, L. Rodman, "Matrices and indefinite scalar products" , Birkhäuser (1983)</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> I.S. [I.S. Iokhvidov] Iohidov, M.G. Krein, H. Langer, "Introduction to the spectral theory of operators in spaces with an indefinite metric" , Akademie Verlag (1982)</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> V.I. Istraţescu, "Inner product spaces. Theory and applications" , Reidel (1987)</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> M.G. Krein, "Introduction to the geometry of indefinite <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055840/k055840406.png" />-spaces and the theory of operators in these spaces" , ''Second Math. Summer School'' , '''1''' , Kiev (1965) pp. 15–92 (In Russian)</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> M.G. Krein, H. Langer, "Ueber einige Fortsetzungsprobleme, die eng mit der Theorie hermitescher Operatoren im Raume <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055840/k055840407.png" /> zusammenhängen, I: Einige Funktionenklassen und ihre Darstellungen" ''Math. Nachr.'' , '''77''' (1977) pp. 187–236</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> H. Langer, "Spectral functions of definitizable operators in Krein spaces" D. Butković (ed.) et al. (ed.) , ''Functional analysis'' , ''Lect. notes in math.'' , '''948''' , Springer (1982) pp. 1–46</TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> H. Langer, "Invariante Teilräume definisierbarer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055840/k055840408.png" />-selbstadjungierter Operatoren" ''Ann. Acad. Sci. Fenn A. I'' , '''475''' (1971)</TD></TR><TR><TD valign="top">[a15]</TD> <TD valign="top"> J. Milnor, D. Husemoller, "Symmetric bilinear forms" , Springer (1973)</TD></TR><TR><TD valign="top">[a16]</TD> <TD valign="top"> R.S. Phillips, "The extensions of dual subspaces invariant under an algebra" , ''Proc. Internat. Symp. Linear Spaces (Jerusalem, 1960)'' , Pergamon (1961) pp. 366–398</TD></TR><TR><TD valign="top">[a17]</TD> <TD valign="top"> L. Bracci, G. Morchio, F. Strocchi, "Wigner's theorem on symmetries in indefinite metric spaces" ''Comm. Math. Phys.'' , '''41''' (1975) pp. 289–299</TD></TR><TR><TD valign="top">[a18]</TD> <TD valign="top"> K.L. Nagy, "State vector spaces with indefinite metric in quantum field theory" , Noordhoff (1966)</TD></TR><TR><TD valign="top">[a19]</TD> <TD valign="top"> M.A. Naimark, R.S. Ismagilov, "Representations of groups and algebras in a space with indefinite metric" ''Itogi Nauk. i Tekhn. Mat. Anal.'' (1969) pp. 73–105 (In Russian)</TD></TR><TR><TD valign="top">[a20]</TD> <TD valign="top"> M.G. Krein, H. Langer, "On some mathematical principles in the linear theory of damped oscillations of continua" ''Integral Equations, Operator Theory'' , '''1''' (1978) pp. 364–399; 539–566 ''Proc. Internat. Symp. Appl. Theory of Functions in Continuum Mechanics, Tbilizi'' , '''2''' (1963) pp. 283–322</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> T.Ya Azizov, I.S. Iokhvidov, "Linear operators in spaces with indefinite metric and their applications" ''Russian Math. Surveys'' , '''15''' (1981) pp. 438–490 ''Itogi Nauk. i Tekhn. Mat. Anal.'' , '''17''' (1979) pp. 113–205</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> T.Ya Azizov, I.S. Iokhvidov, "Foundations of the theory of linear operators in spaces with indefinite metric" , Moscow (1986) (In Russian)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> T. Ando, "Linear operators in Krein spaces" , Hokkaido Univ. (1979)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> J. Bognár, "Indefinite inner product spaces" , Springer (1974)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> Yu.L. Daletskii, M.G. Krein, "Stability of solutions of differential equations in Banach space" , Amer. Math. Soc. (1974) (Translated from Russian)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> A. Dijksma, H. Langer, H.S.V. de Snoo, "Unitary colligations in Krein spaces and their role in the extension theory of isometries and symmetric linear relations in Hilbert spaces" S. Kurepa (ed.) et al. (ed.) , ''Foundational analysis II'' , ''Lect. notes in math.'' , '''1247''' , Springer (1987) pp. 1–42</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> A. Dijksma, H. Langer, H.S.V. de Snoo, "Symmetric Sturm–Liouville operators with eigenvalues depending boundary conditions" , ''Oscillation, Bifurcations and Chaos'' , ''CMS Conf. Proc.'' , '''8''' , Amer. Math. Soc. (1987) pp. 87–116</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> I. [I. Gokhberg] Gohberg, P. Lancaster, L. Rodman, "Matrices and indefinite scalar products" , Birkhäuser (1983)</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> I.S. [I.S. Iokhvidov] Iohidov, M.G. Krein, H. Langer, "Introduction to the spectral theory of operators in spaces with an indefinite metric" , Akademie Verlag (1982)</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> V.I. Istraţescu, "Inner product spaces. Theory and applications" , Reidel (1987)</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> M.G. Krein, "Introduction to the geometry of indefinite <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055840/k055840406.png" />-spaces and the theory of operators in these spaces" , ''Second Math. Summer School'' , '''1''' , Kiev (1965) pp. 15–92 (In Russian)</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> M.G. Krein, H. Langer, "Ueber einige Fortsetzungsprobleme, die eng mit der Theorie hermitescher Operatoren im Raume <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055840/k055840407.png" /> zusammenhängen, I: Einige Funktionenklassen und ihre Darstellungen" ''Math. Nachr.'' , '''77''' (1977) pp. 187–236</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> H. Langer, "Spectral functions of definitizable operators in Krein spaces" D. Butković (ed.) et al. (ed.) , ''Functional analysis'' , ''Lect. notes in math.'' , '''948''' , Springer (1982) pp. 1–46</TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> H. Langer, "Invariante Teilräume definisierbarer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055840/k055840408.png" />-selbstadjungierter Operatoren" ''Ann. Acad. Sci. Fenn A. I'' , '''475''' (1971)</TD></TR><TR><TD valign="top">[a15]</TD> <TD valign="top"> J. Milnor, D. Husemoller, "Symmetric bilinear forms" , Springer (1973)</TD></TR><TR><TD valign="top">[a16]</TD> <TD valign="top"> R.S. Phillips, "The extensions of dual subspaces invariant under an algebra" , ''Proc. Internat. Symp. Linear Spaces (Jerusalem, 1960)'' , Pergamon (1961) pp. 366–398</TD></TR><TR><TD valign="top">[a17]</TD> <TD valign="top"> L. Bracci, G. Morchio, F. Strocchi, "Wigner's theorem on symmetries in indefinite metric spaces" ''Comm. Math. Phys.'' , '''41''' (1975) pp. 289–299</TD></TR><TR><TD valign="top">[a18]</TD> <TD valign="top"> K.L. Nagy, "State vector spaces with indefinite metric in quantum field theory" , Noordhoff (1966)</TD></TR><TR><TD valign="top">[a19]</TD> <TD valign="top"> M.A. Naimark, R.S. Ismagilov, "Representations of groups and algebras in a space with indefinite metric" ''Itogi Nauk. i Tekhn. Mat. Anal.'' (1969) pp. 73–105 (In Russian)</TD></TR><TR><TD valign="top">[a20]</TD> <TD valign="top"> M.G. Krein, H. Langer, "On some mathematical principles in the linear theory of damped oscillations of continua" ''Integral Equations, Operator Theory'' , '''1''' (1978) pp. 364–399; 539–566 ''Proc. Internat. Symp. Appl. Theory of Functions in Continuum Mechanics, Tbilizi'' , '''2''' (1963) pp. 283–322</TD></TR></table> | ||
Revision as of 22:15, 5 June 2020
Let $ {\mathcal K} $
be a complex linear space on a which a Hermitian sesquilinear form $ [ \cdot , \cdot ] $
is defined (i.e. a mapping $ [ \cdot , \cdot ] : {\mathcal K} \times {\mathcal K} \rightarrow \mathbf C $
such that $ [ \alpha _ {1} x _ {1} + \alpha _ {2} x _ {2} , y ] = \alpha _ {1} [ x _ {1} , y ] + \alpha _ {2} [ x _ {2} , y ] $
and $ [ x , y ] = \overline{ {[ y , x ] }}\; $
for all $ x _ {1} , x _ {2} , x , y \in {\mathcal K} $,
$ \alpha _ {1} , \alpha _ {2} \in \mathbf C $).
Then $ {\mathcal K} $(
or, more exactly, $ ( {\mathcal K} , [ \cdot , \cdot ] ) $)
is called a Krein space if in $ {\mathcal K} $
there are two linear manifolds $ {\mathcal K} _ \pm $
such that
$$ \tag{a1 } {\mathcal K} = {\mathcal K} _ {+} \dot{+} {\mathcal K} _ {-} , $$
$ ( {\mathcal K} _ {+} , [ \cdot , \cdot ] ) $ and $ ( {\mathcal K} _ {-} , - [ \cdot , \cdot ] ) $ are Hilbert spaces (cf. Hilbert space) and $ [ {\mathcal K} _ {+} , {\mathcal K} _ {-} ] = \{ 0 \} $. It is always assumed that $ {\mathcal K} _ {+} , {\mathcal K} _ {-} \neq \{ 0 \} $( otherwise $ ( {\mathcal K} , [ \cdot , \cdot ] ) $ or $ ( {\mathcal K} , - [ \cdot , \cdot ] ) $ is a Hilbert space); $ [ \cdot , \cdot ] $ is called the indefinite inner product of the Krein space $ {\mathcal K} $. If, in particular, $ \kappa = \min ( \mathop{\rm dim} {\mathcal K} _ {+} , \mathop{\rm dim} {\mathcal K} _ {-} ) < \infty $, then $ {\mathcal K} _ {-} $ is a $ \pi _ \kappa $- space or Pontryagin space of index $ \kappa $( cf. also Pontryagin space); in the sequel, for a $ \pi _ \kappa $- space it is always assumed that $ \kappa = \mathop{\rm dim} {\mathcal K} _ {+} $.
Using the decomposition (a1), on the Krein space $ ( {\mathcal K} , [ \cdot , \cdot ] ) $ a Hilbert inner product $ ( \cdot , \cdot ) $ can be defined as follows:
$$ \tag{a2 } ( x , y ) = [ x _ {+} , y _ {+} ] - [ x _ {-} , y _ {-} ] , $$
$$ x = x _ {+} + x _ {-} ,\ y = y _ {+} + y _ {-} ,\ x _ \pm , y _ \pm \in {\mathcal K} _ {+} . $$
Although the decomposition (a1) is not unique, the decompositions of the components $ {\mathcal K} _ \pm $ are uniquely determined and the Hilbert norms, generated by different decompositions (a1) according to (a2), are equivalent. All topological notions in a Krein space, if not stated explicitly otherwise, refer to this topology. In the Hilbert space $ ( {\mathcal K} , ( \cdot , \cdot ) ) $, the orthogonal projections onto $ {\mathcal K} _ {+} $ and $ {\mathcal K} _ {-} $ are denoted by $ P _ {+} $ and $ P _ {-} $, respectively. Then for the operator $ J = P _ {+} - P _ {-} $, called a fundamental symmetry, one has
$$ \tag{a3 } [ x , y ] = ( J x , y ) ,\ \ x , y \in {\mathcal K} , $$
and $ J $ has the properties: $ J ^ {2} = I $, $ J = J ^ {*} $. Conversely, given a Hilbert space $ ( {\mathcal K} , ( \cdot , \cdot ) ) $ and in it an operator $ J $ with these properties (or, more generally, an operator $ G $ with $ G = G ^ {*} $, $ 0 \in \rho ( G) $), then an indefinite inner product is defined on $ {\mathcal K} $ by (a3) (or, respectively, by the relation
$$ \tag{a4 } [ x , y ] = ( G x , y ) ,\ \ x , y \in {\mathcal K} \textrm{ ) } , $$
and $ ( {\mathcal K} , [ \cdot , \cdot ] ) $ is a Krein space. Because of this construction, Krein spaces are sometimes called $ J $- spaces.
If, more generally, a Hilbert space $ ( {\mathcal H} , ( \cdot , \cdot ) ) $ and a bounded self-adjoint, not semi-definite, operator $ G $ in $ {\mathcal H} $ are given, the relation (a4) with $ x , y \in {\mathcal H} $ defines a Hermitian sesquilinear form $ [ \cdot , \cdot ] $ on $ {\mathcal H} $. This form can be extended by continuity to the completion of the quotient space $ {\mathcal H} / \mathop{\rm Ker} G $ with respect to the norm $ \| | G | ^ {1/2} x \| $( $ x \in {\mathcal H} $). This completion, equipped with $ [ \cdot , \cdot ] $, is a Krein space containing $ {\mathcal H} / \mathop{\rm Ker} G $ as a dense subset.
If $ r $ is a real and locally summable function on $ \mathbf R $ which assumes positive and negative values on sets of positive Lebesgue measure, then the space $ L _ {2,r} $ of all (classes of) measurable functions (cf. Measurable function) $ f $ on $ \mathbf R $ such that $ \int _ {- \infty } ^ \infty | f | ^ {2} | r | d x < \infty $ and equipped with the indefinite inner product $ [ f , g ] = \int _ {- \infty } ^ \infty f \overline{g}\; r d x $( $ f , g \in L _ {2,r} $) is a Krein space. More generally, if $ \sigma $ is a real function which is locally of bounded variation and not isotone on $ \mathbf R $ and $ | \sigma | $ denotes its total variation, then the space $ L _ {2} ( \sigma ) $, of all measurable functions $ f $ such that $ \int _ {- \infty } ^ \infty | f | ^ {2} d | \sigma | < \infty $ and equipped with the indefinite inner product $ [ f , g ] = \int _ {- \infty } ^ {- \infty } f \overline{g}\; d \sigma $( $ f , g \in L _ {2} ( \sigma ) $) is a Krein space.
Further, a complex linear space with a Hermitian sesquilinear form $ [ \cdot , \cdot ] $, which has $ \kappa $ negative squares (that is, each linear manifold $ {\mathcal L} \subset {\mathcal K} $ with $ [ x , x ] < 0 $ for $ x \in {\mathcal L} $, $ x \neq 0 $, is of dimension $ \leq \kappa $ and at least one such manifold is of dimension $ \kappa $), can be canonically imbedded into a $ \pi _ \kappa $- space by taking a quotient space and completing it (see [a4], [a2], [a9], [a11]).
The indefinite inner product $ [ \cdot , \cdot ] $ on the Krein space $ {\mathcal K} $ gives rise to a classification of the elements of $ {\mathcal K} $: $ x \in {\mathcal K} $ is called positive, non-negative, neutral, etc. if $ [ x , x ] > 0 $, $ [ x , x ] < 0 $, $ [ x , x ] = 0 $, etc. A linear manifold or a subspace $ {\mathcal L} $ in $ {\mathcal K} $ is called positive, non-negative, neutral, etc. if all its non-zero elements are positive, non-negative, neutral, etc. The set of all, e.g., non-negative elements is not linear, but it contains subspaces, and among them maximal ones, called maximal non-negative subspaces. All maximal non-negative subspaces of the Krein space $ {\mathcal K} $ have the same dimension (as $ {\mathcal K} _ {+} $). A subspace $ {\mathcal L} $ of $ {\mathcal K} $( with the decomposition (a1)) is maximal non-negative if and only if it can be written as $ {\mathcal L} = \{ {x _ {+} + K _ {\mathcal L} x _ {+} } : {x _ {+} \in {\mathcal K} _ {+} } \} $, where $ K _ {\mathcal L} $, the angular operator of $ {\mathcal L} $, is a contraction from $ ( {\mathcal K} _ {+} , [ \cdot , \cdot ] ) $ into $ ( {\mathcal K} _ {-} , [ \cdot , \cdot ] ) $. A dual pair $ ( {\mathcal L} _ {+} , {\mathcal L} _ {-} ) $ of subspaces of $ {\mathcal K} $ is defined as follows: $ {\mathcal L} _ {+} $ is a non-negative subspace, $ {\mathcal L} _ {-} $ is a non-positive subspace and $ [ {\mathcal L} _ {+} , {\mathcal L} _ {-} ] = \{ 0 \} $. Any dual pairs is contained in a maximal dual pair (maximality of dual pairs is defined in a natural way by inclusion); in a maximal dual pair $ ( {\mathcal L} _ {+} , {\mathcal L} _ {-} ) $ the subspace $ {\mathcal L} _ {+} $( respectively, $ {\mathcal L} _ {-} $) is maximal non-negative (respectively, non-positive) (R.S. Phillips).
Using the indefinite inner product, orthogonality can be defined in $ {\mathcal K} $: $ x , y \in {\mathcal K} $ are called orthogonal if $ [ x , y ] = 0 $; if $ {\mathcal L} \subset {\mathcal K} $, then $ {\mathcal L} ^ \perp = \{ {x } : {[ x , {\mathcal L} ] = \{ 0 \} } \} $. Some properties of orthogonality in a Hilbert space are preserved; however, there are also essential differences; e.g., $ {\mathcal L} \cap {\mathcal L} ^ \perp $ can contain non-zero vectors; $ {\mathcal L} \cap {\mathcal L} ^ \perp $ coincides with $ {\mathcal L} $ if $ {\mathcal L} $ is neutral, and $ {\mathcal L} \cap {\mathcal L} ^ \perp = \{ 0 \} $ is equivalent to $ \overline{ {{\mathcal L} + {\mathcal L} ^ \perp }}\; = {\mathcal K} $.
For a densely-defined linear operator $ T $ in the Krein space $ ( {\mathcal K} , [ \cdot , \cdot ] ) $ an adjoint $ T ^ { + } $( sometimes called $ J $- adjoint) is defined by $ [ T x , y ] = [ x , T ^ { + } y ] $( $ x \in {\mathcal D} ( T) $, $ y \in {\mathcal D} ( T ^ { + } ) $). If $ T ^ { * } $ denotes the adjoint of $ T $ in the Hilbert space $ ( {\mathcal K} , ( \cdot , \cdot ) ) $( see (a2)), then evidently $ T ^ { + } = J T ^ { * } J $. Now in the Krein space $ {\mathcal K} $ classes of operators are defined more or less similarly to the case of a Hilbert space: $ T $ is symmetric if $ T \subset T ^ { + } $, self-adjoint if $ T = T ^ { + } $, dissipative if $ \mathop{\rm Im} [ T x , x ] \geq 0 $( $ x \in {\mathcal D} ( T) $), contractive if $ [ T x , T x ] \leq [ x , x ] $( $ x \in {\mathcal K} $), unitary if $ T $ is bounded, $ {\mathcal D} ( T) = {\mathcal K} $ and $ T ^ { + } T = I = T T ^ { + } $, etc. Also, new classes of operators arise: E.g., $ T $ is a plus-operator if $ [ x , x ] \geq 0 $ implies $ [ T x , T x ] \geq 0 $, and a doubly plus-operator if $ T $ and $ T ^ { + } $ are plus-operators. In a Krein space a densely-defined isometric operator $ T $( i.e. $ [ T x , T y ] = [ x , y ] $ for all $ x , y \in {\mathcal D} ( T) $) need not be continuous. As in a Hilbert space, self-adjoint and unitary, symmetric and isometric, dissipative and contractive operators are related by the Cayley transform. E.g., if $ A = A ^ {+} $, $ z _ {0} \neq \overline{z}\; _ {0} $ and $ z _ {0} \in \rho ( A) $, then $ U = ( A - \overline{z}\; _ {0} ) ( A - z _ {0} ) ^ {-} 1 $ is unitary.
The spectrum of a self-adjoint operator $ A $ in a Krein space is not necessarily real (it can even cover the whole plane), but it is symmetric with respect to the real axis. Similarly, the spectrum of a unitary operator is symmetric with respect to the unit circle.
The indefinite inner product sometimes gives a classification of the points of the spectrum of an operator: An eigen value is said to be of positive type (negative type, etc.) if the corresponding eigen space is positive (negative, etc.).
If $ \lambda $, $ \overline \lambda \; $ are isolated eigen values of the self-adjoint operator $ A $ in a Krein space, then for the corresponding Riesz projections $ E _ \lambda $, $ E _ {\overline \lambda \; } $ one has $ E _ {\overline \lambda \; } = E _ \lambda ^ {+} $, and if, e.g., $ \mathop{\rm dim} {\mathcal R} ( E _ \lambda ) < \infty $, then the restrictions $ A \mid _ { {\mathcal R} ( E _ \lambda ) } $ and $ A \mid _ { {\mathcal R} ( E _ {\overline \lambda \; } ) } $ have the same Jordan structure. If in a $ \pi _ \kappa $- space the symmetric operator $ A $ has a real non-semi-simple eigen value $ \lambda $, then the corresponding algebraic eigen space $ {\mathcal E} _ \lambda $ can be decomposed into a direct orthogonal sum: $ {\mathcal E} _ \lambda = {\mathcal E} _ \lambda ^ { \prime } + {\mathcal E} _ \lambda ^ { \prime\prime } $, where $ {\mathcal E} _ \lambda ^ { \prime\prime } $ is a positive subspace contained in the geometric eigen space of $ A $ at $ \lambda $, and $ {\mathcal E} _ \lambda ^ { \prime } \neq \{ 0 \} $ is invariant under $ A $ with $ \mathop{\rm dim} {\mathcal E} _ \lambda ^ { \prime } < \infty $; if $ d _ {1} \dots d _ {r} $ are the lengths of the Jordan chains of $ A \mid _ { {\mathcal E} _ \lambda ^ { \prime } } $, one puts $ \rho ( \lambda )= \sum _ {j=} 1 ^ \kappa [ d _ {j} /2 ] $; if $ \lambda $ is a non-real eigen value of $ A $, one defines $ \rho ( \lambda ) $ as the dimension of the corresponding algebraic eigen space. Then $ \sum \rho ( \lambda ) \leq \kappa $, where the sum extends over all eigen values $ \lambda $ of $ A $ in the closed upper half-plane. In particular, the length of any Jordan chain of $ A $ is $ \leq 2 \kappa + 1 $, and the number of eigen values of $ A $ in the open upper half-plane, and also the number of non-semi-simple eigen values of $ A $, does not exceed $ \kappa $.
Specific results for Krein spaces are statements about the existence of maximal non-negative (or maximal non-positive) subspaces, which are invariant under a given operator. The first general result of this type was proved by L.S. Pontryagin in 1944, stating that a self-adjoint operator in a $ \pi _ \kappa $- space has a $ \kappa $- dimensional non-positive (that is, a maximal non-positive) invariant subspace. Subsequently, similar results were proved for various classes of operators in Krein spaces. E.g., a bounded linear operator $ T $ in a Krein space has a maximal non-negative invariant subspace if $ P _ {+} T P _ {-} $ is compact and, additionally, $ T $ is self-adjoint or dissipative or unitary or a plus-operator, etc. (see [a2], [a4]). One possibility for proving these results, e.g. for a unitary operator $ T $, is to establish the existence of a fixed point $ K _ {0} $ of the fractional-linear transformation
$$ K \rightarrow ( T _ {21} + T _ {22} K ) ( T _ {11} + T _ {12} K ) ^ {-} 1 , $$
where $ K $ is a contraction from $ {\mathcal K} _ {+} $ into $ {\mathcal K} _ {-} $( an angular operator) and $ ( T _ {ij} ) _ {1} ^ {2} $ is the matrix representation of $ T $ with respect to (a1). By different methods also in other cases the existence of a maximal non-negative invariant subspace has been proved, e.g.: 1) $ T $ is unitary and $ \| T ^ { n } \| $ is uniformly bounded for all $ n = 0 , 1 ,\dots $; 2) $ [ T x , T x ] > [ x , x ] $ for all $ x \in {\mathcal K} $, $ x \neq 0 $, and $ \sigma ( T) \cap \{ | \rho | = 1 \} = \emptyset $; and 3) $ T $ is bounded, self-adjoint and there exists a polynomial $ p $ such that $ [ p ( T) x , x ] \geq 0 $( $ x \in {\mathcal K} $). In many cases these maximal non-positive invariant subspaces $ {\mathcal L} $ can be specified by properties of the spectrum of $ A \mid _ {\mathcal L} $. E.g., if $ T $ is bounded, self-adjoint and $ P _ {+} T P _ {-} $ is compact, then $ {\mathcal L} $ can be chosen such that $ \mathop{\rm Im} \sigma ( A \mid _ {\mathcal L} ) \geq 0 $. There are also results about the existence of a common invariant maximal non-positive subspace for a commuting family of operators, e.g.: A commuting family of bounded self-adjoint operators in a $ \pi _ \kappa $- space has a common maximal non-negative invariant subspace (M.A. Naimark; for applications in the representation theory of groups in $ \pi _ \kappa $- spaces see [a19]). Phillips asked ([a16]) if a dual pair of subspaces of $ {\mathcal K} $ which are invariant under a commutative algebra $ A $ of bounded self-adjoint operators in the Krein space $ {\mathcal K} $ can always be extended to a maximal dual pair whose subspaces are still invariant under $ A $( which would imply that each bounded self-adjoint operator in $ {\mathcal K} $ has a maximal non-negative invariant subspace). Only partial solutions to this problem are known (cf. [a4], [a2], [a14]).
A self-adjoint operator $ A $ in the Krein space $ {\mathcal K} $ is called definitizable (positizable in [a4]) if $ \rho ( A) \neq \emptyset $ and if there exists a polynomial $ p $ such that $ [ p ( A) x , x ] \geq 0 $( $ x \in {\mathcal D} ( p ( A) ) $). Each self-adjoint operator $ A $ in a $ \pi _ \kappa $- space has this property (where $ p $ can be chosen to be $ q \overline{q}\; $ with $ q $ the minimal polynomial of $ A \mid _ {\mathcal L} $, $ {\mathcal L} $ being a $ \kappa $- dimensional non-positive invariant subspace of $ A $); also, each self-adjoint operator $ A $ in a Krein space for which $ \rho ( A ) \neq \emptyset $ and for which the Hermitian sesquilinear form $ [ A x , y ] $( $ x , y \in {\mathcal D} ( A) $) has a finite number of negative squares, is definitizable.
The non-real spectrum $ \sigma _ {0} ( A) $ of the definitizable operator $ A $ consists of at most finitely many eigen values, and $ A $ has a spectral function, with possibly certain critical points [a13], [a2]. This means that there is a finite set $ c ( A) \subset \mathbf R \cup \{ \infty \} $( of critical points) such that on the semi-ring $ \mathbf R _ {A} $, consisting of all bounded intervals of $ \mathbf R $ with end points not in $ c ( A) $ and their complements, a homomorphism $ E $ with values in the set of all self-adjoint projections in the Krein space $ {\mathcal K} $ is defined, such that for $ \Delta \in \mathbf R _ {A} $: a) $ E ( \Delta ) {\mathcal K} $ is a positive (negative) subspace if $ p > 0 $( respectively, $ p < 0 $) on $ \overline \Delta \; \cap \sigma ( A) $ for some definitizing polynomial $ p $ of $ A $; b) $ E ( \Delta ) $ is in the double commutant of the resolvent of $ A $; and c) if $ \Delta $ is bounded, then $ E ( \Delta ) {\mathcal K} \subset {\mathcal D} ( A) $ and $ \sigma ( A \mid _ {E ( \Delta ) {\mathcal K} } ) \subset \overline \Delta \; $, $ \sigma ( A \mid _ {( I - E ( \Delta ) ) {\mathcal K} } ) \subset \overline{ {( \mathbf R \setminus \Delta ) }}\; \cup \sigma _ {0} ( A) $. If, in particular, $ A $ is bounded and $ [ A x , x ] \geq 0 $( $ x \in {\mathcal K} $), then $ c ( A) \subset \{ 0 \} $, and one has
$$ A x = \int\limits _ {- \| A \| } ^ { {\| } A \| } \lambda E ( d \lambda ) x + N x , $$
for some bounded operator $ N $ such that $ N = N ^ {+} $, $ N ^ {2} = 0 $, $ [ N x , x ] \geq 0 $( $ x \in {\mathcal K} $).
If the spectrum of a definitizable operator $ A $ is discrete, then the linear span of its algebraic eigen spaces is dense in $ {\mathcal K} $; if $ A $ is compact and self-adjoint in a $ \pi _ \kappa $- space $ {\mathcal K} $ and $ 0 \notin \sigma _ {p} ( A) $, then there is a Riesz basis of $ {\mathcal K} $ consisting of eigen and associated vectors of $ A $( I.S. Iokhvidov).
There is a theory of extensions of symmetric operators to self-adjoint operators and of generalized resolvents in $ \pi _ \kappa $- spaces, and also in Krein spaces, which is similar to the Hilbert space situation. The same is true for dilation theory: Each bounded linear operator $ T $ in a Krein space $ {\mathcal K} $ has a unitary dilation $ T $ in some Krein space $ {\mathcal K} tilde \supset {\mathcal K} $([a2]). In this context one has the following result: Let $ {\mathcal K} _ {1} $, $ {\mathcal K} _ {2} $ be Krein spaces, $ {\mathcal D} $ a simply-connected open domain with smooth boundary such that $ 0 \in {\mathcal D} $, $ \overline{ {\mathcal D} }\; \subset \{ {z } : {| z | < 1 } \} $, and let $ \Theta $ be a function which is holomorphic in $ {\mathcal D} $ whose values are bounded linear operators from $ {\mathcal K} _ {1} $ to $ {\mathcal K} _ {2} $. Then there exists a Krein space $ {\mathcal K} $ and a unitary operator
$$ U = \left ( \begin{array}{ll} U _ {11} &U _ {12} \\ U _ {21} &U _ {22} \\ \end{array} \right ) : {\mathcal K} \oplus {\mathcal K} _ {1} \rightarrow {\mathcal K} \oplus {\mathcal K} _ {2} , $$
such that
$$ \Theta ( z) = U _ {22} + z U _ {21} ( I - z U _ {11} ) ^ {-} 1 U _ {12} \ \ ( z \in {\mathcal D} ) $$
(T.Ya. Azizov, see [a2], [a6]; here unitary means that $ U $ maps the Krein space $ {\mathcal K} \oplus {\mathcal K} _ {1} $ continuously onto the Krein space $ {\mathcal K} \oplus {\mathcal K} _ {2} $, preserving the indefinite inner product).
Some of the first papers about Krein spaces or, more generally, spaces with indefinite inner product, were stimulated by problems of (quantum) mechanics ([a4], [a2]; see also [a18], [a17]). Operators in Krein spaces arise also in a natural way in problems in mathematical analysis. Some examples of these are: I) Consider the canonical system of differential equations $ J \dot{x} ( t) = i H ( t) x ( t) $ on $ [ 0 , \infty ) $, where $ H ( t) $, $ J $ are $ ( n \times n ) $ matrices, $ H ( t ) \geq 0 $, $ J = J ^ {*} = J ^ {-} 1 $, and let $ U ( t) $ be the corresponding matrizant (cf. Cauchy operator): $ J \dot{U} ( t) = i H ( t) U ( t) $, $ U ( 0) = I _ {n} $. Then $ U ( t) $ is $ J $- unitary (that is, unitary with respect to the inner product defined in $ \mathbf C ^ {n} $ by the matrix $ J $, see (a3)), and, e.g., in the stability theory for periodic equations $ ( H ( t) = H ( T + t ) ) $ the classification of the eigen values of $ U ( T) $ into those of positive or negative type plays an essential role ([a5], [a8]). II) The integral operator $ x ( \cdot ) \rightarrow \int _ {a} ^ {b} K ( \cdot , s ) x ( s ) d \sigma ( s) $, $ \sigma $ real and of bounded variation on the interval $ [ a , b ] $, $ K ( s , t ) = \overline{ {K ( t , s ) }}\; $( $ s , t \in [ a , b ] $), is self-adjoint in the Krein space $ L _ {2} ( \sigma ) $. III) The theory of dual pairs of subspaces of a Krein space and their extensions to maximal dual pairs is related to certain questions in the theory of extensions of dissipative operators in a Hilbert space to maximal dissipative ones. Phillips started these investigations in connection with the Cauchy problem for dissipative hyperbolic and parabolic systems (see [a2], [a4] for references). IV) With the monic operator polynomial $ L ( \lambda ) = \lambda ^ {n} I + \lambda ^ {n-} 1 B _ {n-} 1 + \dots + \lambda B _ {1} + B _ {0} $, $ B _ {j} $ bounded self-adjoint operators in some Hilbert space $ {\mathcal H} $, one can associate the so-called companion operator
$$ A = \left ( \begin{array}{ccccc} - B _ {n-} 1 &- B _ {n-} 2 &\dots &- B _ {1} &- B _ {0} \\ I & 0 &\dots & 0 & 0 \\ \cdot &\cdot &\dots &\cdot &\cdot \\ 0 & 0 &\dots & I & 0 \\ \end{array} \right ) , $$
which is self-adjoint in the Krein space $ {\mathcal K} = {\mathcal H} ^ {n} $, $ [ x , y ] = ( G x , y ) $( $ x , y \in {\mathcal H} ^ {n} $), where $ ( \cdot , \cdot ) $ is the inner product in $ {\mathcal H} ^ {n} $ and
$$ G = \left ( \begin{array}{cccc} 0 & 0 &\dots & I \\ 0 & 0 &{} &B _ {n-} 1 \\ \cdot &\cdot &{} &\cdot \\ \cdot &\cdot &{} &\cdot \\ \cdot &\cdot &{} &\cdot \\ I &B _ {n-} 1 &\dots &B _ {1} \\ \end{array} \right ) . $$
If, e.g., $ n = 2 $ and $ B _ {0} $ is compact and $ \geq 0 $, the results about the existence of maximal non-negative invariant subspaces mentioned above imply that there exists a bounded linear operator $ Z $ in $ {\mathcal H} $ satisfying $ Z ^ {2} + B _ {1} Z + B _ {0} = 0 $, $ Z ^ {*} Z \leq B _ {0} $ and $ \mathop{\rm Im} \sigma ( Z) \geq 0 $[a12]. In a similar way, if $ B \geq 0 $, $ C = C ^ {*} $ and $ A $ are $ ( n \times n ) $ matrices such that $ G = ( _ { A } ^ {-} C {} _ {B} ^ {A ^ {*} } ) $ has $ n $ positive and $ n $ negative eigen values, the solutions $ X $ of the matrix Riccati equation
$$ X B X + X A + A ^ {*} X - C = 0 $$
with $ ( X ^ {*} - X ) ( A + B X ) \geq 0 $ are in bijective correspondence with all maximal non-positive subspaces which are invariant under the self-adjoint operator $ T = i ( _ {C} ^ {A} {} _ {- A ^ {*} } ^ { B } ) $ in the $ 2n $- dimensional Krein space $ {\mathcal K} = \mathbf C ^ {2n} $, equipped with the indefinite inner product (a4) (see [a8]). V) If $ L $ is a formally-symmetric regular ordinary differential operator on the interval $ [ a , b ] $ with symmetric boundary conditions at $ a $ and $ b $, and $ r $ is a summable function on $ [ a , b ] $ which is not of constant sign (a.e.) on $ [ a , b ] $, then the differential equation $ L y - \lambda r y = r f $ leads to a self-adjoint operator $ A $ in the Krein space $ {\mathcal K} = L _ {2,r} $ with inner product $ [ f , g ] = \int _ {a} ^ {b} f \overline{g}\; r d x $. If $ L $ is semi-bounded from below, the operator $ A $ is definitizable. VI) Krein spaces can be associated with certain eigen value problems for ordinary differential operators containing the eigen value parameters in the boundary conditions. E.g., consider in $ L _ {2} = L _ {2} [ 0 , \infty ) $ the problem
$$ - \frac{d ^ {2} y }{d x ^ {2} } + q y - \lambda y = f , $$
which is supposed to have a limit point at $ \infty $ and with a boundary condition $ \alpha ( \lambda ) y ( 0) + \beta ( \lambda ) y ^ \prime ( 0) = 0 $ at $ x = 0 $( $ \alpha $, $ \beta $ are functions which are holomorphic on some set $ D _ {\alpha , \beta } \subset \mathbf C $ and satisfying a symmetry condition). The solution of this problem can be represented as $ y = P ( A - \lambda I ) ^ {-} 1 f $( $ f \in L _ {2} $), where, in general, $ A $ is a self-adjoint operator in some Krein space $ {\mathcal K} = L _ {2} \oplus {\mathcal K} _ {1} $ and $ P $ is the orthogonal projection from $ {\mathcal K} $ onto $ L _ {2} $[a17]. VII) Certain classes of analytic functions are closely related to the theory of operators in $ \pi _ \kappa $- spaces. This concerns, e.g., functions $ f $ which are defined and meromorphic in the upper half-plane (or the unit disc) and which are such that the kernel
$$ N _ {f} ( z , \rho ) = \ \frac{f ( z) - \overline{ {f ( \rho ) }}\; }{z - \overline \rho \; } $$
(or
$$ \left . S _ {f} ( z , \overline \rho \; ) = \ \frac{1 - f ( z) \overline{ {f ( \rho ) }}\; }{1 - z \overline \rho \; } \right ) $$
has $ \kappa $ negative squares (that is, for arbitrary $ n $ and $ z _ {1} \dots z _ {n} $, the matrix $ ( N _ {f} ( z _ {i} , z _ {j} ) ) _ {1} ^ {n} $ has at most $ n $ negative eigen values and for at least one choice of $ n , z _ {1} \dots z _ {n} $ it has $ \kappa $ negative eigen values). Corresponding extrapolation or moment problems can be treated by making use of results of the theory of symmetric or isometric operators in $ \pi _ \kappa $- spaces (see [a12], [a2]).
References
| [a1] | T.Ya Azizov, I.S. Iokhvidov, "Linear operators in spaces with indefinite metric and their applications" Russian Math. Surveys , 15 (1981) pp. 438–490 Itogi Nauk. i Tekhn. Mat. Anal. , 17 (1979) pp. 113–205 |
| [a2] | T.Ya Azizov, I.S. Iokhvidov, "Foundations of the theory of linear operators in spaces with indefinite metric" , Moscow (1986) (In Russian) |
| [a3] | T. Ando, "Linear operators in Krein spaces" , Hokkaido Univ. (1979) |
| [a4] | J. Bognár, "Indefinite inner product spaces" , Springer (1974) |
| [a5] | Yu.L. Daletskii, M.G. Krein, "Stability of solutions of differential equations in Banach space" , Amer. Math. Soc. (1974) (Translated from Russian) |
| [a6] | A. Dijksma, H. Langer, H.S.V. de Snoo, "Unitary colligations in Krein spaces and their role in the extension theory of isometries and symmetric linear relations in Hilbert spaces" S. Kurepa (ed.) et al. (ed.) , Foundational analysis II , Lect. notes in math. , 1247 , Springer (1987) pp. 1–42 |
| [a7] | A. Dijksma, H. Langer, H.S.V. de Snoo, "Symmetric Sturm–Liouville operators with eigenvalues depending boundary conditions" , Oscillation, Bifurcations and Chaos , CMS Conf. Proc. , 8 , Amer. Math. Soc. (1987) pp. 87–116 |
| [a8] | I. [I. Gokhberg] Gohberg, P. Lancaster, L. Rodman, "Matrices and indefinite scalar products" , Birkhäuser (1983) |
| [a9] | I.S. [I.S. Iokhvidov] Iohidov, M.G. Krein, H. Langer, "Introduction to the spectral theory of operators in spaces with an indefinite metric" , Akademie Verlag (1982) |
| [a10] | V.I. Istraţescu, "Inner product spaces. Theory and applications" , Reidel (1987) |
| [a11] | M.G. Krein, "Introduction to the geometry of indefinite 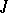 -spaces and the theory of operators in these spaces" , Second Math. Summer School , 1 , Kiev (1965) pp. 15–92 (In Russian) -spaces and the theory of operators in these spaces" , Second Math. Summer School , 1 , Kiev (1965) pp. 15–92 (In Russian) |
| [a12] | M.G. Krein, H. Langer, "Ueber einige Fortsetzungsprobleme, die eng mit der Theorie hermitescher Operatoren im Raume 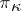 zusammenhängen, I: Einige Funktionenklassen und ihre Darstellungen" Math. Nachr. , 77 (1977) pp. 187–236 zusammenhängen, I: Einige Funktionenklassen und ihre Darstellungen" Math. Nachr. , 77 (1977) pp. 187–236 |
| [a13] | H. Langer, "Spectral functions of definitizable operators in Krein spaces" D. Butković (ed.) et al. (ed.) , Functional analysis , Lect. notes in math. , 948 , Springer (1982) pp. 1–46 |
| [a14] | H. Langer, "Invariante Teilräume definisierbarer 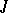 -selbstadjungierter Operatoren" Ann. Acad. Sci. Fenn A. I , 475 (1971) -selbstadjungierter Operatoren" Ann. Acad. Sci. Fenn A. I , 475 (1971) |
| [a15] | J. Milnor, D. Husemoller, "Symmetric bilinear forms" , Springer (1973) |
| [a16] | R.S. Phillips, "The extensions of dual subspaces invariant under an algebra" , Proc. Internat. Symp. Linear Spaces (Jerusalem, 1960) , Pergamon (1961) pp. 366–398 |
| [a17] | L. Bracci, G. Morchio, F. Strocchi, "Wigner's theorem on symmetries in indefinite metric spaces" Comm. Math. Phys. , 41 (1975) pp. 289–299 |
| [a18] | K.L. Nagy, "State vector spaces with indefinite metric in quantum field theory" , Noordhoff (1966) |
| [a19] | M.A. Naimark, R.S. Ismagilov, "Representations of groups and algebras in a space with indefinite metric" Itogi Nauk. i Tekhn. Mat. Anal. (1969) pp. 73–105 (In Russian) |
| [a20] | M.G. Krein, H. Langer, "On some mathematical principles in the linear theory of damped oscillations of continua" Integral Equations, Operator Theory , 1 (1978) pp. 364–399; 539–566 Proc. Internat. Symp. Appl. Theory of Functions in Continuum Mechanics, Tbilizi , 2 (1963) pp. 283–322 |
Krein space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Krein_space&oldid=47525