Difference between revisions of "K-system(2)"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | k0550202.png | ||
| + | $#A+1 = 44 n = 3 | ||
| + | $#C+1 = 44 : ~/encyclopedia/old_files/data/K055/K.0505020 \BMI K\EMI\AAhsystem | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | '' $ \{ T ^ {t} \} $'' | |
| − | + | A [[Measurable flow|measurable flow]] ( $ K $- | |
| + | flow) or cascade ( $ K $- | ||
| + | cascade) in a [[Lebesgue space|Lebesgue space]] such that there is a measurable partition (cf. [[Measurable decomposition|Measurable decomposition]]) $ \xi $ | ||
| + | of the phase space with the following properties: a) it is increasing (formerly called invariant) with respect to $ \{ T ^ {t} \} $, | ||
| + | that is, $ T ^ {t} \xi $ | ||
| + | is a refinement $ \mathop{\rm mod} 0 $ | ||
| + | of $ \xi $ | ||
| + | when $ t > 0 $; | ||
| + | b) it is a two-sided generator for $ \{ T ^ {t} \} $, | ||
| + | that is, the only measurable partition $ \mathop{\rm mod} 0 $ | ||
| + | that is finer $ \mathop{\rm mod} 0 $ | ||
| + | than all the $ T ^ {t} \xi $ | ||
| + | is the partition into points; and c) the only measurable partition $ \mathop{\rm mod} 0 $ | ||
| + | that is coarser $ \mathop{\rm mod} 0 $ | ||
| + | than all the $ T ^ {t} \xi $ | ||
| + | is the trivial partition, whose only element is the whole phase space. | ||
| − | + | An automorphism of a measure space whose iterations form a $ K $- | |
| + | cascade is called a $ K $- | ||
| + | automorphism. If $ \{ T ^ {t} \} $ | ||
| + | is a $ K $- | ||
| + | system, then all $ T ^ {t} $ | ||
| + | with $ t \neq 0 $ | ||
| + | are $ K $- | ||
| + | automorphisms. Conversely, given a measurable flow or cascade $ \{ T ^ {t} \} $, | ||
| + | if just one $ T ^ {t} $ | ||
| + | is a $ K $- | ||
| + | automorphism, then $ \{ T ^ {t} \} $ | ||
| + | is a $ K $- | ||
| + | system. $ K $- | ||
| + | systems posses strong ergodic properties: positive entropy (cf. [[Entropy theory of a dynamical system|Entropy theory of a dynamical system]]) and [[Ergodicity|ergodicity]]; [[Mixing|mixing]] of all degrees and they have a countably-multiple Lebesgue spectrum (see [[Spectrum of a dynamical system|Spectrum of a dynamical system]]; and also [[#References|[2]]]). | ||
| − | Given a measurable flow or cascade in a Lebesgue space, if one of the | + | An endomorphism of a Lebesgue space has completely-positive entropy if all its non-trivial quotient endomorphisms have positive entropy. Among these are the $ K $- |
| + | automorphisms (namely, they are just the automorphisms with completely-positive entropy) and also other interesting objects (exact endomorphisms; cf. [[Exact endomorphism|Exact endomorphism]]). The notion of a $ K $- | ||
| + | system can be generalized in other directions: to the case of an infinite invariant measure (see [[#References|[6]]], [[#References|[7]]], [[#References|[11]]]) and for the action of groups other than $ \mathbf R $ | ||
| + | and $ \mathbf Z $( | ||
| + | see [[#References|[8]]]–[[#References|[10]]], [[#References|[12]]]). | ||
| + | |||
| + | $ K $- | ||
| + | systems are sometimes called Kolmogorov systems (flows, etc.), after their originator (see ), who used the term "quasi-regular dynamical systemquasi-regular" . This emphasizes the analogy with regular random processes (see [[#References|[4]]]). If a random process $ \{ X _ {t} \} $, | ||
| + | stationary in the narrow sense of the word, is interpreted as a dynamical system, then the values of the process "in the past" define a certain increasing measurable partition $ \xi $, | ||
| + | which is the smallest with respect to which all the $ X _ {t} $ | ||
| + | with $ t < 0 $ | ||
| + | are measurable. If $ \xi $ | ||
| + | has the properties b) and c) above (the "all or nothing" law), then the process is called regular. In particular, this probabilistic form presents the simplest example of a $ K $- | ||
| + | automorphism: a [[Bernoulli automorphism|Bernoulli automorphism]]. | ||
| + | |||
| + | Given a measurable flow or cascade in a Lebesgue space, if one of the $ T ^ {t} $ | ||
| + | is isomorphic to a Bernoulli automorphism, then they all are (when $ t \neq 0 $). | ||
| + | In this case the dynamical system is called Bernoullian (see [[#References|[5]]]). There are $ K $- | ||
| + | systems that are not Bernoullian. $ K $- | ||
| + | systems (even Bernoullian ones) arise naturally not only in probability theory, but also in problems of an algebraic, geometric and even physical nature (see [[#References|[2]]], [[#References|[3]]], [[#References|[5]]], [[#References|[13]]], [[#References|[14]]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1a]</TD> <TD valign="top"> A.N. Kolmogorov, "A new metric invariant of transitive dynamical systems and of endomorphisms of Lebesgue spaces" ''Dokl. Akad. Nauk SSSR'' , '''119''' : 5 (1958) pp. 861–864 (In Russian)</TD></TR><TR><TD valign="top">[1b]</TD> <TD valign="top"> A.N. Kolmogorov, "On the entropy as a metric invariant of automorphisms" ''Dokl. Akad. Nauk SSSR'' , '''124''' : 4 (1959) pp. 754–755 (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I.P. [I.P. Kornfel'd] Cornfel'd, S.V. Fomin, Ya.G. Sinai, "Ergodic theory" , Springer (1982) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A.B. Katok, Ya.G. Sinai, A.M. Stepin, "Theory of dynamical systems and general transformation groups with invariant measure" ''J. Soviet Math.'' , '''7''' (1977) pp. 974–1065 ''Itogi Nauk i Tekhn. Mat. Anal.'' , '''13''' (1975) pp. 129–262</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> Yu.A. Rozanov, "Stationary random processes" , Holden-Day (1967) (Translated from Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> D. Ornstein, "Ergodic theory, randomness, and dynamical systems" , Yale Univ. Press (1974)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> W. Parry, "Ergodic and spectral analysis of certain infinite measure preserving transformations" ''Proc. Amer. Math. Soc.'' , '''16''' : 5 (1965) pp. 960–966</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> J.K. Dugdale, "Kolmogorov automorphisms in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055020/k05502051.png" />-finite measure spaces" ''Publ. Math. Debrecen'' , '''14''' (1967) pp. 79–81</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> J.P. Conze, "Entropie d'un groupe abélien de transformations" ''Z. Wahrsch. Verw. Gebiete'' , '''25''' : 1 (1972) pp. 11–30</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> R.M. Burton, "An asymptotic definition of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055020/k05502052.png" />-groups of automorphisms" ''Z. Wahrsch. Verw. Gebiete'' , '''47''' : 2 (1979) pp. 207–212</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> S. Dani, "Kolmogorov automorphisms on homogeneous spaces" ''Amer. J. Math.'' , '''98''' : 1 (1976) pp. 119–163</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> U. Krengel, L. Sucheston, "Note on shift-invariant sets" ''Ann. Math. Statist.'' , '''40''' : 2 (1969) pp. 694–696</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> B. Kamiński, "A note on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055020/k05502053.png" />-systems" ''Bull. Acad. Polon. Sci. Sér. Sci. Math. Astr. Phys.'' , '''26''' : 2 (1978) pp. 95–97</TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> Ya.G. Sinai, et al., "Dynamical systems" , '''4''' , Springer (1988) (Translated from Russian)</TD></TR><TR><TD valign="top">[14]</TD> <TD valign="top"> N.F.G. Martin, J.W. England, "Mathematical theory of entropy" , Addison-Wesley (1981)</TD></TR></table> | <table><TR><TD valign="top">[1a]</TD> <TD valign="top"> A.N. Kolmogorov, "A new metric invariant of transitive dynamical systems and of endomorphisms of Lebesgue spaces" ''Dokl. Akad. Nauk SSSR'' , '''119''' : 5 (1958) pp. 861–864 (In Russian)</TD></TR><TR><TD valign="top">[1b]</TD> <TD valign="top"> A.N. Kolmogorov, "On the entropy as a metric invariant of automorphisms" ''Dokl. Akad. Nauk SSSR'' , '''124''' : 4 (1959) pp. 754–755 (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I.P. [I.P. Kornfel'd] Cornfel'd, S.V. Fomin, Ya.G. Sinai, "Ergodic theory" , Springer (1982) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A.B. Katok, Ya.G. Sinai, A.M. Stepin, "Theory of dynamical systems and general transformation groups with invariant measure" ''J. Soviet Math.'' , '''7''' (1977) pp. 974–1065 ''Itogi Nauk i Tekhn. Mat. Anal.'' , '''13''' (1975) pp. 129–262</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> Yu.A. Rozanov, "Stationary random processes" , Holden-Day (1967) (Translated from Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> D. Ornstein, "Ergodic theory, randomness, and dynamical systems" , Yale Univ. Press (1974)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> W. Parry, "Ergodic and spectral analysis of certain infinite measure preserving transformations" ''Proc. Amer. Math. Soc.'' , '''16''' : 5 (1965) pp. 960–966</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> J.K. Dugdale, "Kolmogorov automorphisms in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055020/k05502051.png" />-finite measure spaces" ''Publ. Math. Debrecen'' , '''14''' (1967) pp. 79–81</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> J.P. Conze, "Entropie d'un groupe abélien de transformations" ''Z. Wahrsch. Verw. Gebiete'' , '''25''' : 1 (1972) pp. 11–30</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> R.M. Burton, "An asymptotic definition of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055020/k05502052.png" />-groups of automorphisms" ''Z. Wahrsch. Verw. Gebiete'' , '''47''' : 2 (1979) pp. 207–212</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> S. Dani, "Kolmogorov automorphisms on homogeneous spaces" ''Amer. J. Math.'' , '''98''' : 1 (1976) pp. 119–163</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> U. Krengel, L. Sucheston, "Note on shift-invariant sets" ''Ann. Math. Statist.'' , '''40''' : 2 (1969) pp. 694–696</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> B. Kamiński, "A note on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055020/k05502053.png" />-systems" ''Bull. Acad. Polon. Sci. Sér. Sci. Math. Astr. Phys.'' , '''26''' : 2 (1978) pp. 95–97</TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> Ya.G. Sinai, et al., "Dynamical systems" , '''4''' , Springer (1988) (Translated from Russian)</TD></TR><TR><TD valign="top">[14]</TD> <TD valign="top"> N.F.G. Martin, J.W. England, "Mathematical theory of entropy" , Addison-Wesley (1981)</TD></TR></table> | ||
Revision as of 22:14, 5 June 2020
$ \{ T ^ {t} \} $
A measurable flow ( $ K $- flow) or cascade ( $ K $- cascade) in a Lebesgue space such that there is a measurable partition (cf. Measurable decomposition) $ \xi $ of the phase space with the following properties: a) it is increasing (formerly called invariant) with respect to $ \{ T ^ {t} \} $, that is, $ T ^ {t} \xi $ is a refinement $ \mathop{\rm mod} 0 $ of $ \xi $ when $ t > 0 $; b) it is a two-sided generator for $ \{ T ^ {t} \} $, that is, the only measurable partition $ \mathop{\rm mod} 0 $ that is finer $ \mathop{\rm mod} 0 $ than all the $ T ^ {t} \xi $ is the partition into points; and c) the only measurable partition $ \mathop{\rm mod} 0 $ that is coarser $ \mathop{\rm mod} 0 $ than all the $ T ^ {t} \xi $ is the trivial partition, whose only element is the whole phase space.
An automorphism of a measure space whose iterations form a $ K $- cascade is called a $ K $- automorphism. If $ \{ T ^ {t} \} $ is a $ K $- system, then all $ T ^ {t} $ with $ t \neq 0 $ are $ K $- automorphisms. Conversely, given a measurable flow or cascade $ \{ T ^ {t} \} $, if just one $ T ^ {t} $ is a $ K $- automorphism, then $ \{ T ^ {t} \} $ is a $ K $- system. $ K $- systems posses strong ergodic properties: positive entropy (cf. Entropy theory of a dynamical system) and ergodicity; mixing of all degrees and they have a countably-multiple Lebesgue spectrum (see Spectrum of a dynamical system; and also [2]).
An endomorphism of a Lebesgue space has completely-positive entropy if all its non-trivial quotient endomorphisms have positive entropy. Among these are the $ K $- automorphisms (namely, they are just the automorphisms with completely-positive entropy) and also other interesting objects (exact endomorphisms; cf. Exact endomorphism). The notion of a $ K $- system can be generalized in other directions: to the case of an infinite invariant measure (see [6], [7], [11]) and for the action of groups other than $ \mathbf R $ and $ \mathbf Z $( see [8]–[10], [12]).
$ K $- systems are sometimes called Kolmogorov systems (flows, etc.), after their originator (see ), who used the term "quasi-regular dynamical systemquasi-regular" . This emphasizes the analogy with regular random processes (see [4]). If a random process $ \{ X _ {t} \} $, stationary in the narrow sense of the word, is interpreted as a dynamical system, then the values of the process "in the past" define a certain increasing measurable partition $ \xi $, which is the smallest with respect to which all the $ X _ {t} $ with $ t < 0 $ are measurable. If $ \xi $ has the properties b) and c) above (the "all or nothing" law), then the process is called regular. In particular, this probabilistic form presents the simplest example of a $ K $- automorphism: a Bernoulli automorphism.
Given a measurable flow or cascade in a Lebesgue space, if one of the $ T ^ {t} $ is isomorphic to a Bernoulli automorphism, then they all are (when $ t \neq 0 $). In this case the dynamical system is called Bernoullian (see [5]). There are $ K $- systems that are not Bernoullian. $ K $- systems (even Bernoullian ones) arise naturally not only in probability theory, but also in problems of an algebraic, geometric and even physical nature (see [2], [3], [5], [13], [14]).
References
| [1a] | A.N. Kolmogorov, "A new metric invariant of transitive dynamical systems and of endomorphisms of Lebesgue spaces" Dokl. Akad. Nauk SSSR , 119 : 5 (1958) pp. 861–864 (In Russian) |
| [1b] | A.N. Kolmogorov, "On the entropy as a metric invariant of automorphisms" Dokl. Akad. Nauk SSSR , 124 : 4 (1959) pp. 754–755 (In Russian) |
| [2] | I.P. [I.P. Kornfel'd] Cornfel'd, S.V. Fomin, Ya.G. Sinai, "Ergodic theory" , Springer (1982) (Translated from Russian) |
| [3] | A.B. Katok, Ya.G. Sinai, A.M. Stepin, "Theory of dynamical systems and general transformation groups with invariant measure" J. Soviet Math. , 7 (1977) pp. 974–1065 Itogi Nauk i Tekhn. Mat. Anal. , 13 (1975) pp. 129–262 |
| [4] | Yu.A. Rozanov, "Stationary random processes" , Holden-Day (1967) (Translated from Russian) |
| [5] | D. Ornstein, "Ergodic theory, randomness, and dynamical systems" , Yale Univ. Press (1974) |
| [6] | W. Parry, "Ergodic and spectral analysis of certain infinite measure preserving transformations" Proc. Amer. Math. Soc. , 16 : 5 (1965) pp. 960–966 |
| [7] | J.K. Dugdale, "Kolmogorov automorphisms in 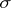 -finite measure spaces" Publ. Math. Debrecen , 14 (1967) pp. 79–81 -finite measure spaces" Publ. Math. Debrecen , 14 (1967) pp. 79–81 |
| [8] | J.P. Conze, "Entropie d'un groupe abélien de transformations" Z. Wahrsch. Verw. Gebiete , 25 : 1 (1972) pp. 11–30 |
| [9] | R.M. Burton, "An asymptotic definition of 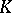 -groups of automorphisms" Z. Wahrsch. Verw. Gebiete , 47 : 2 (1979) pp. 207–212 -groups of automorphisms" Z. Wahrsch. Verw. Gebiete , 47 : 2 (1979) pp. 207–212 |
| [10] | S. Dani, "Kolmogorov automorphisms on homogeneous spaces" Amer. J. Math. , 98 : 1 (1976) pp. 119–163 |
| [11] | U. Krengel, L. Sucheston, "Note on shift-invariant sets" Ann. Math. Statist. , 40 : 2 (1969) pp. 694–696 |
| [12] | B. Kamiński, "A note on 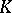 -systems" Bull. Acad. Polon. Sci. Sér. Sci. Math. Astr. Phys. , 26 : 2 (1978) pp. 95–97 -systems" Bull. Acad. Polon. Sci. Sér. Sci. Math. Astr. Phys. , 26 : 2 (1978) pp. 95–97 |
| [13] | Ya.G. Sinai, et al., "Dynamical systems" , 4 , Springer (1988) (Translated from Russian) |
| [14] | N.F.G. Martin, J.W. England, "Mathematical theory of entropy" , Addison-Wesley (1981) |
K-system(2). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=K-system(2)&oldid=47474