Difference between revisions of "Invariant average"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | i0522101.png | ||
| + | $#A+1 = 70 n = 1 | ||
| + | $#C+1 = 70 : ~/encyclopedia/old_files/data/I052/I.0502210 Invariant average, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | ''invariant mean, on a group or semi-group $ G $, | |
| + | more precisely, an invariant mean or average on a space $ X $ | ||
| + | of functions on $ G $'' | ||
| − | + | A continuous [[Linear functional|linear functional]] $ m $ | |
| + | on a closed subspace $ X $ | ||
| + | of the space $ B ( G ) $ | ||
| + | of all bounded complex-valued functions on $ G $, | ||
| + | endowed with the supremum norm, that contains the constant functions and is invariant under the operation of complex conjugation, and where $ m $ | ||
| + | and $ X $ | ||
| + | satisfy the following conditions: 1) $ X $ | ||
| + | is invariant under left translation, that is, if $ f \in X $ | ||
| + | then so is $ {} _ {x} f \in X $, | ||
| + | where $ {} _ {x} f ( t ) = f ( xt ) $ | ||
| + | for all $ x , t \in G $, | ||
| + | $ f \in X $; | ||
| + | 2) $ m $ | ||
| + | is a mean on $ X $, | ||
| + | that is, $ m ( \overline{f}\; ) = \overline{ {m ( f ) }}\; $ | ||
| + | for all $ f \in X $ | ||
| + | and $ \inf \{ f ( x ) \} \leq m ( f ) \leq \sup \{ f ( x ) \} $ | ||
| + | for all real-valued $ f \in X $; | ||
| + | and 3) $ m ( {} _ {x} f ) = m( f ) $ | ||
| + | for all $ f \in X $ | ||
| + | and all $ x \in G $. | ||
| + | In this case the invariant mean $ m $ | ||
| + | is called a left-invariant mean; right-invariant and two-sided invariant means on $ G $ | ||
| + | are defined similarly. | ||
| − | for all continuous functions | + | If there exists on $ X = B ( G ) $ |
| + | a two-sided invariant mean, then the group $ G $ | ||
| + | is called amenable. Amenability of a group $ G $ | ||
| + | is related to the existence of invariant measures (cf. [[Invariant measure|Invariant measure]]) with respect to certain transformation groups related to $ G $( | ||
| + | see [[#References|[1]]]). If $ G $ | ||
| + | is a locally compact [[Topological group|topological group]], then there exists on the spaces of almost-periodic functions and weakly almost-periodic functions on $ G $ | ||
| + | a non-trivial left-invariant mean. On the other hand, the following conditions are equivalent: 1) there exists a left-invariant mean on the space $ X = L _ \infty ( G ) $; | ||
| + | 2) there exists a left-invariant mean on the space $ X = CB ( G ) $ | ||
| + | of bounded continuous complex-valued functions on $ G $; | ||
| + | 3) there exists a left-invariant mean on the space $ X = UCB ( G ) $ | ||
| + | of uniformly-continuous bounded complex-valued functions; 4) there exists a two-sided invariant mean on one of the spaces $ L _ \infty ( G ) $, | ||
| + | $ CB ( G ) $, | ||
| + | $ UCB ( G ) $; | ||
| + | 5) the group $ G $ | ||
| + | does not have a [[Complementary series (of representations)|complementary series (of representations)]]; 6) the support of the [[Regular representation|regular representation]] of $ G $ | ||
| + | coincides with the dual space of $ G $; | ||
| + | 7) the unit function on $ G $ | ||
| + | can be uniformly approximated on any compactum $ K \subset G $ | ||
| + | by finite linear combinations of matrix entries of the regular representation of $ G $; | ||
| + | 8) if $ \mu $ | ||
| + | is a left [[Haar measure|Haar measure]] on $ G $ | ||
| + | and $ \nu $ | ||
| + | is a bounded complex-valued regular [[Borel measure|Borel measure]] on $ G $ | ||
| + | such that | ||
| + | |||
| + | $$ | ||
| + | \int\limits \int\limits f ( s ) f \overline{ {( t ^ {-} 1 s ) }}\; d \mu ( s ) d \nu ( t ) \geq \ | ||
| + | 0 | ||
| + | $$ | ||
| + | |||
| + | for all continuous functions $ f $ | ||
| + | with compact support in $ G $, | ||
| + | then $ \int _ {G} d \nu \geq 0 $; | ||
| + | 9) there exists for some $ q > 1 $, | ||
| + | $ q \neq \infty $, | ||
| + | any $ \epsilon > 0 $, | ||
| + | and any compactum $ K \subset G $ | ||
| + | a non-negative function $ \phi \in L _ {q} ( G ) $, | ||
| + | $ \| \phi \| _ {q} = 1 $, | ||
| + | such that $ \| {} _ {x} \phi - \phi \| _ {q} < \epsilon $ | ||
| + | for all $ x \in K $; | ||
| + | 10) the preceding condition holds for all $ q > 1 $, | ||
| + | $ q \neq \infty $; | ||
| + | 11) there exists for any $ \epsilon > 0 $ | ||
| + | and any compactum $ K \subset G $ | ||
| + | a Borel set $ U \subset G $ | ||
| + | such that $ 0 < \mu ( U ) < \infty $ | ||
| + | and $ \mu ^ {-} 1 ( U ) \mu ( x U \Delta U ) < \epsilon $ | ||
| + | for all $ x \in K $; | ||
| + | and 12) any continuous action of $ G $ | ||
| + | on a compact convex subset of a locally convex space by continuous affine transformations has a fixed point. A locally compact group satisfying any of the equivalent conditions 1)–12) is called amenable. Continuous images of amenable groups, closed subgroups of amenable groups, extensions of amenable groups by amenable groups, and inductive limits of amenable groups are amenable. A uniformly-bounded representation of an amenable group in a Hilbert space is equivalent to a [[Unitary representation|unitary representation]] in the same space. Some of the results listed above can be extended to the case of general topological groups admitting an invariant mean on the space of bounded continuous complex-valued functions. The theory of invariant means and amenable groups has important applications in the theory of dynamical systems, ergodic theory, the theory of von Neumann algebras, and abstract harmonic analysis (cf. also [[Harmonic analysis, abstract|Harmonic analysis, abstract]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> J. von Neumann, "Zur allgemeiner Theorie des Masses" ''Fund. Math.'' , '''13''' (1929) pp. 73–116</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> F. Greenleaf, "Invariant means on topological groups and their applications" , v. Nostrand-Reinhold (1969)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Dixmier, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052210/i05221071.png" /> algebras" , North-Holland (1977) (Translated from French)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> J. von Neumann, "Zur allgemeiner Theorie des Masses" ''Fund. Math.'' , '''13''' (1929) pp. 73–116</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> F. Greenleaf, "Invariant means on topological groups and their applications" , v. Nostrand-Reinhold (1969)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Dixmier, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052210/i05221071.png" /> algebras" , North-Holland (1977) (Translated from French)</TD></TR></table> | ||
Revision as of 22:13, 5 June 2020
invariant mean, on a group or semi-group $ G $,
more precisely, an invariant mean or average on a space $ X $
of functions on $ G $
A continuous linear functional $ m $ on a closed subspace $ X $ of the space $ B ( G ) $ of all bounded complex-valued functions on $ G $, endowed with the supremum norm, that contains the constant functions and is invariant under the operation of complex conjugation, and where $ m $ and $ X $ satisfy the following conditions: 1) $ X $ is invariant under left translation, that is, if $ f \in X $ then so is $ {} _ {x} f \in X $, where $ {} _ {x} f ( t ) = f ( xt ) $ for all $ x , t \in G $, $ f \in X $; 2) $ m $ is a mean on $ X $, that is, $ m ( \overline{f}\; ) = \overline{ {m ( f ) }}\; $ for all $ f \in X $ and $ \inf \{ f ( x ) \} \leq m ( f ) \leq \sup \{ f ( x ) \} $ for all real-valued $ f \in X $; and 3) $ m ( {} _ {x} f ) = m( f ) $ for all $ f \in X $ and all $ x \in G $. In this case the invariant mean $ m $ is called a left-invariant mean; right-invariant and two-sided invariant means on $ G $ are defined similarly.
If there exists on $ X = B ( G ) $ a two-sided invariant mean, then the group $ G $ is called amenable. Amenability of a group $ G $ is related to the existence of invariant measures (cf. Invariant measure) with respect to certain transformation groups related to $ G $( see [1]). If $ G $ is a locally compact topological group, then there exists on the spaces of almost-periodic functions and weakly almost-periodic functions on $ G $ a non-trivial left-invariant mean. On the other hand, the following conditions are equivalent: 1) there exists a left-invariant mean on the space $ X = L _ \infty ( G ) $; 2) there exists a left-invariant mean on the space $ X = CB ( G ) $ of bounded continuous complex-valued functions on $ G $; 3) there exists a left-invariant mean on the space $ X = UCB ( G ) $ of uniformly-continuous bounded complex-valued functions; 4) there exists a two-sided invariant mean on one of the spaces $ L _ \infty ( G ) $, $ CB ( G ) $, $ UCB ( G ) $; 5) the group $ G $ does not have a complementary series (of representations); 6) the support of the regular representation of $ G $ coincides with the dual space of $ G $; 7) the unit function on $ G $ can be uniformly approximated on any compactum $ K \subset G $ by finite linear combinations of matrix entries of the regular representation of $ G $; 8) if $ \mu $ is a left Haar measure on $ G $ and $ \nu $ is a bounded complex-valued regular Borel measure on $ G $ such that
$$ \int\limits \int\limits f ( s ) f \overline{ {( t ^ {-} 1 s ) }}\; d \mu ( s ) d \nu ( t ) \geq \ 0 $$
for all continuous functions $ f $ with compact support in $ G $, then $ \int _ {G} d \nu \geq 0 $; 9) there exists for some $ q > 1 $, $ q \neq \infty $, any $ \epsilon > 0 $, and any compactum $ K \subset G $ a non-negative function $ \phi \in L _ {q} ( G ) $, $ \| \phi \| _ {q} = 1 $, such that $ \| {} _ {x} \phi - \phi \| _ {q} < \epsilon $ for all $ x \in K $; 10) the preceding condition holds for all $ q > 1 $, $ q \neq \infty $; 11) there exists for any $ \epsilon > 0 $ and any compactum $ K \subset G $ a Borel set $ U \subset G $ such that $ 0 < \mu ( U ) < \infty $ and $ \mu ^ {-} 1 ( U ) \mu ( x U \Delta U ) < \epsilon $ for all $ x \in K $; and 12) any continuous action of $ G $ on a compact convex subset of a locally convex space by continuous affine transformations has a fixed point. A locally compact group satisfying any of the equivalent conditions 1)–12) is called amenable. Continuous images of amenable groups, closed subgroups of amenable groups, extensions of amenable groups by amenable groups, and inductive limits of amenable groups are amenable. A uniformly-bounded representation of an amenable group in a Hilbert space is equivalent to a unitary representation in the same space. Some of the results listed above can be extended to the case of general topological groups admitting an invariant mean on the space of bounded continuous complex-valued functions. The theory of invariant means and amenable groups has important applications in the theory of dynamical systems, ergodic theory, the theory of von Neumann algebras, and abstract harmonic analysis (cf. also Harmonic analysis, abstract).
References
| [1] | J. von Neumann, "Zur allgemeiner Theorie des Masses" Fund. Math. , 13 (1929) pp. 73–116 |
| [2] | F. Greenleaf, "Invariant means on topological groups and their applications" , v. Nostrand-Reinhold (1969) |
| [3] | J. Dixmier, "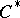 algebras" , North-Holland (1977) (Translated from French) algebras" , North-Holland (1977) (Translated from French) |
Invariant average. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Invariant_average&oldid=47411