Difference between revisions of "Integral-relation method"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | i0516101.png | ||
| + | $#A+1 = 54 n = 0 | ||
| + | $#C+1 = 54 : ~/encyclopedia/old_files/data/I051/I.0501610 Integral\AAhrelation method, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''strip method'' | ''strip method'' | ||
| Line 5: | Line 17: | ||
Suppose one has a system of partial differential equations in divergence form | Suppose one has a system of partial differential equations in divergence form | ||
| − | + | $$ \tag{1 } | |
| + | |||
| + | \frac \partial {\partial x } | ||
| + | P _ {i} ( x , y , u _ {1} \dots u _ {k} ) + | ||
| + | |||
| + | \frac \partial {\partial y } | ||
| + | Q _ {i} ( x , y , u _ {1} \dots u _ {k} ) = | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | = \ | ||
| + | F _ {i} ( x , y , u _ {1} \dots u _ {k} ) ,\ i = 1 \dots k, | ||
| + | $$ | ||
| + | |||
| + | where $ P _ {i} $, | ||
| + | $ Q _ {i} $, | ||
| + | $ F _ {i} $ | ||
| + | are given functions in the independent variables $ x $, | ||
| + | $ y $ | ||
| + | and in the unknown variables $ u _ {1} \dots u _ {k} $. | ||
| + | Suppose further that a solution to (1) is sought for in the curvilinear rectangle with boundary $ x = a $, | ||
| + | $ x = b $, | ||
| + | $ y = 0 $, | ||
| + | $ y = \Delta ( x) $, | ||
| + | on which $ 2k $ | ||
| + | conditions are posed, and where $ k $ | ||
| + | of them are posed on $ x = a $ | ||
| + | and $ x = b $. | ||
| + | If the function $ \Delta ( x) $ | ||
| + | is unknown in advance, one only needs one additional condition. If the boundary contains singular points, then instead of corresponding boundary conditions one uses regularity conditions. | ||
| − | + | In the $ N $- | |
| + | th approximation the domain of integration is decomposed into $ N $ | ||
| + | strips by the lines $ y = y _ {n} ( x) = n \Delta ( x) / N $, | ||
| + | $ n = 1 \dots N $. | ||
| + | For each $ N $ | ||
| + | one chooses a closed system of $ N $ | ||
| + | linearly independent functions $ f _ {n} ( y) $. | ||
| + | By multiplying each initial equation in (1) by $ f _ {n} ( y) $ | ||
| + | and after integration, with respect to $ y $, | ||
| + | across all strips, one obtains $ kN $ | ||
| + | integral relations of the form | ||
| − | + | $$ | |
| + | \left . | ||
| + | \frac{d}{dx} | ||
| + | \int\limits _ { 0 } ^ { \Delta ( x) } f _ {n} ( y) P dy - | ||
| + | \Delta ^ \prime ( x) f _ {n} ( \Delta ( x) ) P \right | _ {y = \Delta ( x) } + | ||
| + | $$ | ||
| − | + | $$ | |
| + | + | ||
| + | \left . f _ {n} ( \Delta ( x)) Q \right | _ {y = \Delta ( x) } - f _ {n} ( 0) Q ( 0) + | ||
| + | $$ | ||
| − | + | $$ | |
| + | - \int\limits _ { 0 } ^ { \Delta ( x) } f _ {n} ^ { \prime } ( y) Q dy | ||
| + | = \int\limits _ { 0 } ^ { \Delta ( x) } f _ {n} ( y) F dy . | ||
| + | $$ | ||
| − | + | The integrals $ P $, | |
| + | $ Q $, | ||
| + | $ F $ | ||
| + | are approximated by using interpolation formulas with respect to their values $ P _ {n} $, | ||
| + | $ Q _ {n} $, | ||
| + | $ F _ {n} $ | ||
| + | on the boundaries of the strips. The integrals participating in the integral relations have the form | ||
| − | + | $$ | |
| + | \int\limits _ { 0 } ^ { \Delta ( x) } f _ {n} ( y) P dy \approx \Delta ( x) | ||
| + | \sum _ { n= } 0 ^ { N } C _ {n} P _ {n} y _ {n} ( x) , | ||
| + | $$ | ||
| − | + | where $ C _ {n} $ | |
| + | are numerical coefficients depending on the choice of the interpolation formulas and the form of the $ f _ {n} ( y) $. | ||
| + | The result is a system of ordinary differential equations, with respect to $ x $, | ||
| + | relative to $ K ( N+ 1) $ | ||
| + | values of the unknown functions $ u _ {n} $ | ||
| + | on the entire boundaries of the strips. This system is closed by $ k $ | ||
| + | boundary conditions for $ y = 0 $ | ||
| + | and $ y = \Delta ( x) $. | ||
| − | + | The functions $ f _ {n} ( y) $ | |
| + | can be chosen rather arbitrarily. Choosing $ f _ {n} ( y) = \delta ( y - y _ {n} ) $, | ||
| + | $ n = 1 \dots N $, | ||
| + | i.e. delta-functions, leads to the method of straight lines. In it the derivatives with respect to $ y $ | ||
| + | are replaced by difference expressions, corresponding to the interpolation formulas chosen. When using the step-functions | ||
| − | + | $$ | |
| + | f _ {n} ( y) = \ | ||
| + | \left \{ | ||
| − | + | \begin{array}{l} | |
| + | 0 \ \textrm{ for } y < y _ {n-} 1 , \\ | ||
| + | 1 \ \textrm{ for } y _ {n-} 1 \leq y \leq y _ {n} , \\ | ||
| + | 0 \ \textrm{ for } y > y _ {n} , \\ | ||
| + | \end{array} | ||
| + | \right . | ||
| + | $$ | ||
| − | + | $ n = 1 \dots N $, | |
| + | one simply speaks of the integral-relation method, and the initial equations are integrated across each strip. Moreover, the conservation laws chosen for (1) are written as the following integral relations for the strips: | ||
| − | + | $$ | |
| − | + | \frac{d}{dx} | |
| + | \int\limits _ { y _ {n-} 1 } ^ { {y _ n } } P dy - y _ {n} ^ \prime | ||
| + | P ( y _ {n} )+ y _ {n-} 1 ^ \prime P ( y _ {n-} 1 ) + Q ( y _ {n} ) - Q ( y _ {n-} 1 ) = | ||
| + | $$ | ||
| − | + | $$ | |
| + | = \ | ||
| + | \int\limits _ { y _ {n-} 1 } ^ { {y _ n } } F dy . | ||
| + | $$ | ||
For systems of quasi-linear hyperbolic-type equations one has investigated convergence and error of the integral-relation method [[#References|[4]]]. In [[#References|[4]]] one has also established results that indicate the superiority of the integral-relation method over that of straight lines. Later papers have investigated analogous results for elliptic-type equations. | For systems of quasi-linear hyperbolic-type equations one has investigated convergence and error of the integral-relation method [[#References|[4]]]. In [[#References|[4]]] one has also established results that indicate the superiority of the integral-relation method over that of straight lines. Later papers have investigated analogous results for elliptic-type equations. | ||
| − | The merits of the integral-relation method are, among others: the possibility of choosing the interpolation formulas and the function | + | The merits of the integral-relation method are, among others: the possibility of choosing the interpolation formulas and the function $ f( y) $ |
| + | in dependence on the behaviour of the solution; the exact integration with respect to one of the variables (a result of the divergence notation of the original equations); the simplicity of the computational algorithm; and the relatively-small amount of computer memory when calculating on a computer. In the integral-relation method one approximates by an integral: this increases the accuracy of the approximation on account of a reduction of the coefficient of the remainder term; the integral is a smoother function than the integrand, thus one may reduce the number of interpolation nodes. If the integrand has discontinuities of the first kind, then the integral is a continuous function. The integral-relation method is most efficient when the solution can be obtained with good accuracy for a small number of strips. | ||
The approximation in two variables of the integral-relation method can be generalized to the case of equations in three variables. Approximation in two variables can be conducted also in the two-dimensional case (the domain of integration is not partitioned into strips but into subdomains then); the system of approximate equations is then a system of non-linear algebraic or transcendental equations. Elements of the integral-relation method are used in other numerical methods, e.g. in the [[Large-particle method|large-particle method]]. | The approximation in two variables of the integral-relation method can be generalized to the case of equations in three variables. Approximation in two variables can be conducted also in the two-dimensional case (the domain of integration is not partitioned into strips but into subdomains then); the system of approximate equations is then a system of non-linear algebraic or transcendental equations. Elements of the integral-relation method are used in other numerical methods, e.g. in the [[Large-particle method|large-particle method]]. | ||
Latest revision as of 22:12, 5 June 2020
strip method
A method for solving a system of partial differential equations, based on approximately reducing a partial differential equation to a system of ordinary differential equations. It is applicable to differential equations of various types. It was introduced by A.A. Dorodnitsyn [1] as a generalization of the method of straight lines, a generalization of it with the introduction of smoothened functions was given in [2], while in [3] the method was evaluated and further developed.
Suppose one has a system of partial differential equations in divergence form
$$ \tag{1 } \frac \partial {\partial x } P _ {i} ( x , y , u _ {1} \dots u _ {k} ) + \frac \partial {\partial y } Q _ {i} ( x , y , u _ {1} \dots u _ {k} ) = $$
$$ = \ F _ {i} ( x , y , u _ {1} \dots u _ {k} ) ,\ i = 1 \dots k, $$
where $ P _ {i} $, $ Q _ {i} $, $ F _ {i} $ are given functions in the independent variables $ x $, $ y $ and in the unknown variables $ u _ {1} \dots u _ {k} $. Suppose further that a solution to (1) is sought for in the curvilinear rectangle with boundary $ x = a $, $ x = b $, $ y = 0 $, $ y = \Delta ( x) $, on which $ 2k $ conditions are posed, and where $ k $ of them are posed on $ x = a $ and $ x = b $. If the function $ \Delta ( x) $ is unknown in advance, one only needs one additional condition. If the boundary contains singular points, then instead of corresponding boundary conditions one uses regularity conditions.
In the $ N $- th approximation the domain of integration is decomposed into $ N $ strips by the lines $ y = y _ {n} ( x) = n \Delta ( x) / N $, $ n = 1 \dots N $. For each $ N $ one chooses a closed system of $ N $ linearly independent functions $ f _ {n} ( y) $. By multiplying each initial equation in (1) by $ f _ {n} ( y) $ and after integration, with respect to $ y $, across all strips, one obtains $ kN $ integral relations of the form
$$ \left . \frac{d}{dx} \int\limits _ { 0 } ^ { \Delta ( x) } f _ {n} ( y) P dy - \Delta ^ \prime ( x) f _ {n} ( \Delta ( x) ) P \right | _ {y = \Delta ( x) } + $$
$$ + \left . f _ {n} ( \Delta ( x)) Q \right | _ {y = \Delta ( x) } - f _ {n} ( 0) Q ( 0) + $$
$$ - \int\limits _ { 0 } ^ { \Delta ( x) } f _ {n} ^ { \prime } ( y) Q dy = \int\limits _ { 0 } ^ { \Delta ( x) } f _ {n} ( y) F dy . $$
The integrals $ P $, $ Q $, $ F $ are approximated by using interpolation formulas with respect to their values $ P _ {n} $, $ Q _ {n} $, $ F _ {n} $ on the boundaries of the strips. The integrals participating in the integral relations have the form
$$ \int\limits _ { 0 } ^ { \Delta ( x) } f _ {n} ( y) P dy \approx \Delta ( x) \sum _ { n= } 0 ^ { N } C _ {n} P _ {n} y _ {n} ( x) , $$
where $ C _ {n} $ are numerical coefficients depending on the choice of the interpolation formulas and the form of the $ f _ {n} ( y) $. The result is a system of ordinary differential equations, with respect to $ x $, relative to $ K ( N+ 1) $ values of the unknown functions $ u _ {n} $ on the entire boundaries of the strips. This system is closed by $ k $ boundary conditions for $ y = 0 $ and $ y = \Delta ( x) $.
The functions $ f _ {n} ( y) $ can be chosen rather arbitrarily. Choosing $ f _ {n} ( y) = \delta ( y - y _ {n} ) $, $ n = 1 \dots N $, i.e. delta-functions, leads to the method of straight lines. In it the derivatives with respect to $ y $ are replaced by difference expressions, corresponding to the interpolation formulas chosen. When using the step-functions
$$ f _ {n} ( y) = \ \left \{ \begin{array}{l} 0 \ \textrm{ for } y < y _ {n-} 1 , \\ 1 \ \textrm{ for } y _ {n-} 1 \leq y \leq y _ {n} , \\ 0 \ \textrm{ for } y > y _ {n} , \\ \end{array} \right . $$
$ n = 1 \dots N $, one simply speaks of the integral-relation method, and the initial equations are integrated across each strip. Moreover, the conservation laws chosen for (1) are written as the following integral relations for the strips:
$$ \frac{d}{dx} \int\limits _ { y _ {n-} 1 } ^ { {y _ n } } P dy - y _ {n} ^ \prime P ( y _ {n} )+ y _ {n-} 1 ^ \prime P ( y _ {n-} 1 ) + Q ( y _ {n} ) - Q ( y _ {n-} 1 ) = $$
$$ = \ \int\limits _ { y _ {n-} 1 } ^ { {y _ n } } F dy . $$
For systems of quasi-linear hyperbolic-type equations one has investigated convergence and error of the integral-relation method [4]. In [4] one has also established results that indicate the superiority of the integral-relation method over that of straight lines. Later papers have investigated analogous results for elliptic-type equations.
The merits of the integral-relation method are, among others: the possibility of choosing the interpolation formulas and the function $ f( y) $ in dependence on the behaviour of the solution; the exact integration with respect to one of the variables (a result of the divergence notation of the original equations); the simplicity of the computational algorithm; and the relatively-small amount of computer memory when calculating on a computer. In the integral-relation method one approximates by an integral: this increases the accuracy of the approximation on account of a reduction of the coefficient of the remainder term; the integral is a smoother function than the integrand, thus one may reduce the number of interpolation nodes. If the integrand has discontinuities of the first kind, then the integral is a continuous function. The integral-relation method is most efficient when the solution can be obtained with good accuracy for a small number of strips.
The approximation in two variables of the integral-relation method can be generalized to the case of equations in three variables. Approximation in two variables can be conducted also in the two-dimensional case (the domain of integration is not partitioned into strips but into subdomains then); the system of approximate equations is then a system of non-linear algebraic or transcendental equations. Elements of the integral-relation method are used in other numerical methods, e.g. in the large-particle method.
The integral-relation method is mostly used in gas dynamics, where a number of practically-important problems have been solved by using it. Three schemes of the integral-relation method have been considered here: 1) the domain of integration is partitioned by lines passing through the surface of the body and the shock waves (Fig.a); 2) the domain of integration is partitioned by lines passing through the axis of symmetry and the boundary characteristics (Fig.b); and 3) the partitioning is into subdomains by two families of intersecting lines (Fig.c).
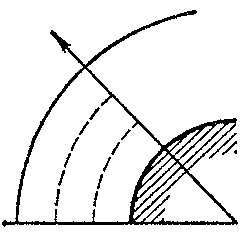
Figure: i051610a
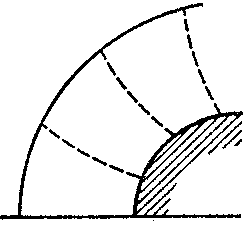
Figure: i051610b
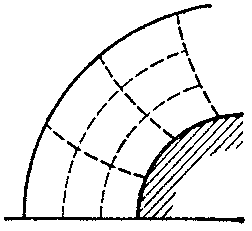
Figure: i051610c
The integral-relation method for computing supersonic flow around the fore part of a blunted body with propagating shock waves was developed in [5], in which a numerical solution to this problem in a direct formulation was obtained for the first time. The solutions for most general cases have been found (bodies of various forms; spatial flow; the flow of a real gas under equilibrium and non-equilibrium physical-chemical changes and radiations; non-stationary motion; and the flow of a viscous gas, [6]). The method has also been used for computing the potential flow of a gas [7], and for solving some mixed problems: flow in sub- and transonic parts of jets [8]. Pre-critical flow around a profile under an angle of attack with a place of the supersonic region has been considered [9]. Supersonic conic gas flow has been clarified by the integral-relation method.
The integral-relation method has found wide application in computing the flow of a viscous gas in the theory of boundary layers. In the laminar incompressible case a solution has been obtained up to the point of discontinuity [2]. Further, laminar boundary layers in a gas taking into account blowing-up or suction, radiation or heath conduction have been calculated. By the integral-relation method one has obtained solutions to the non-stationary problem of a point one-dimensional discontinuity in a gas taking counter-pressure into account, as well as in a gas with infinite conductivity in the presence of a magnetic field and in a heated gas.
References
| [1] | A.A. Dorodnitsyn, "On a method for numerically solving certain nonlinear problems of aerohydrodynamics" , Proc. third All-Union Math. Congress , 3 , Moscow (1956) pp. 447–453 (In Russian) |
| [2] | A.A. Dorodnitsyn, "On a method for solving the laminar boundary layer equation" Zh. Priklad. Mekh. i Tekhn. Fiz. , 1 : 3 (1960) pp. 111–118 (In Russian) |
| [3] | O.M. Belotserkovskii, P.I. Chushkin, "A numerical method of integral relations" USSR Comp. Math. Math. Phys. , 2 (1963) pp. 823–858 Zh. Vychisl. Mat. Mat. Fiz. , 2 : 5 (1962) pp. 731–759 |
| [4] | V.V. Bobkov, V.I. Krylov, "The method of integral relations for equations and systems of hyperbolic type" Differentsial'nye Uravneniya , 1 : 2 (1965) pp. 230–243 (In Russian) |
| [5] | O.M. Belotserkovskii, "Flow around a circular cylinder with a detached shockwave" Dokl. Akad. Nauk SSSR , 113 : 3 (1957) pp. 509–512 (In Russian) |
| [6] | O.M. Belotserkovskii, et al., "Flow of a supersonic gas around blunted bodies; theoretical and experimental investigations" , Moscow (1967) (In Russian) |
| [7] | P.I. Chuskin, "Subsonic gas flow around ellipses and ellipsoids" Vychisl. Mat. , 2 (1957) pp. 20–44 (In Russian) |
| [8] | Ya.I. Alikhashkin, A.P. Favorskii, P.I. Chushkin, "On the calculation of the flow in a plane laval nozzle" USSR Comp. Math. Math. Phys. , 3 : 6 (1963) pp. 1552–1558 Zh. Vychisl. Mat. Mat. Fiz. , 3 : 6 (1963) pp. 1130–1134 |
| [9] | T.C. Tai, "Transonic inviscid flow over lifting airfoils by the method of integral relations" J. AIAA , 12 (1974) pp. 798–804 |
| [10] | V.P. Korobeinikov, P.I. Chushkin, "Plane, cylindrical, and spherical explosions in a gas with counterpressure" Proc. Steklov Inst. Math. , 87 (1967) pp. 1–40 Trudy Mat. Inst. Steklov. , 87 (1966) pp. 4–34 |
Integral-relation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral-relation_method&oldid=47363