|
|
| Line 1: |
Line 1: |
| − | A representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i0507301.png" /> of a locally compact group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i0507302.png" /> induced by a representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i0507303.png" /> of a closed subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i0507304.png" /> (cf. [[Representation of a group|Representation of a group]]). More precisely, it is a representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i0507305.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i0507306.png" /> in some space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i0507307.png" /> of functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i0507308.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i0507309.png" /> taking values in the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073010.png" /> of the representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073011.png" /> and satisfying the condition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073012.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073013.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073014.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073015.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073016.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073017.png" />. The induced representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073018.png" /> is usually denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073019.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073020.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073021.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073022.png" />, or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073023.png" />. The operation of constructing an induced representation is the simplest and most important stage in the construction of representations of more complicated groups by starting from representations of simpler groups, and for a wide class of groups a complete description of the irreducible representations can be given in terms of induced representations or their generalizations.
| + | <!-- |
| | + | i0507301.png |
| | + | $#A+1 = 189 n = 2 |
| | + | $#C+1 = 189 : ~/encyclopedia/old_files/data/I050/I.0500730 Induced representation |
| | + | Automatically converted into TeX, above some diagnostics. |
| | + | Please remove this comment and the {{TEX|auto}} line below, |
| | + | if TeX found to be correct. |
| | + | --> |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073024.png" /> is a finite group, then the inducing representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073025.png" /> is assumed to be finite-dimensional, while the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073026.png" /> is considered to be the space of all functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073027.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073028.png" /> taking values in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073029.png" /> and satisfying the condition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073030.png" />. The representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073031.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073032.png" /> is the identity representation of the identity subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073033.png" />, is the right [[Regular representation|regular representation]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073034.png" />; the representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073035.png" /> is equivalent to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073036.png" />. The representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073037.png" /> is equivalent to the representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073038.png" /> in the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073039.png" /> of all functions on the homogeneous space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073040.png" /> with values in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073041.png" />, defined by formulas of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073042.png" />, where the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073043.png" /> is defined as follows: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073044.png" /> is some mapping satisfying the condition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073045.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073046.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073047.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073048.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073049.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073050.png" />. The function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073051.png" /> is a one-dimensional cocycle of the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073052.png" /> with coefficients in the group of functions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073053.png" /> with values in the invertible operators in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073054.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073055.png" /> is equivalent to a representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073056.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073057.png" /> is equivalent to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073058.png" />; the representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073059.png" /> is equivalent to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073060.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073061.png" /> are subgroups of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073062.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073063.png" /> and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073064.png" /> is a representation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073065.png" />, then the representation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073066.png" /> induced by the representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073067.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073068.png" /> is equivalent to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073069.png" /> (the theorem on the composition of induced representations). If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073070.png" /> are representations of the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073071.png" /> and the subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073072.png" />, respectively, then the spaces of intertwining operators (cf. [[Intertwining operator|Intertwining operator]]) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073073.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073074.png" /> are isomorphic, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073075.png" /> is the restriction of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073076.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073077.png" /> (Frobenius' reciprocity theorem). In particular, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073078.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073079.png" /> are irreducible, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073080.png" /> occurs in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073081.png" /> with the same multiplicity as that with which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073082.png" /> occurs in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073083.png" />. The character <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073084.png" /> of the induced representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073085.png" /> of the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073086.png" /> is defined by the formula:
| + | {{TEX|auto}} |
| | + | {{TEX|done}} |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073087.png" /></td> </tr></table>
| + | A representation $ \pi $ |
| | + | of a locally compact group $ G $ |
| | + | induced by a representation $ \rho $ |
| | + | of a closed subgroup $ H $( |
| | + | cf. [[Representation of a group|Representation of a group]]). More precisely, it is a representation $ \pi $ |
| | + | of $ G $ |
| | + | in some space $ E $ |
| | + | of functions $ f $ |
| | + | on $ G $ |
| | + | taking values in the space $ V $ |
| | + | of the representation $ \rho $ |
| | + | and satisfying the condition $ f ( hg ) = \rho ( h) f ( g ) $ |
| | + | for all $ g \in G $, |
| | + | $ h \in H $, |
| | + | where $ [ \pi ( g _ {1} ) f ] ( g ) = f ( g g _ {1} ) $ |
| | + | for all $ f \in E $, |
| | + | $ g , g _ {1} \in G $. |
| | + | The induced representation $ \pi $ |
| | + | is usually denoted by $ \mathop{\rm Ind} \rho $, |
| | + | $ \mathop{\rm Ind} _ {H} ^ {G} \rho $, |
| | + | $ U ^ \rho $, |
| | + | $ {} _ {H} U ^ \rho $, |
| | + | or $ {} _ {H} U _ {G} ^ \rho $. |
| | + | The operation of constructing an induced representation is the simplest and most important stage in the construction of representations of more complicated groups by starting from representations of simpler groups, and for a wide class of groups a complete description of the irreducible representations can be given in terms of induced representations or their generalizations. |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073088.png" /> is the character of the representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073089.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073090.png" /> extended by zero to the entire group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073091.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073092.png" /> runs through the set of representatives of the right cosets of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073093.png" /> by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073094.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073095.png" /> be subgroups of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073096.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073097.png" /> be a representation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073098.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i05073099.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730100.png" /> and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730101.png" /> be the representation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730102.png" /> induced by the representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730103.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730104.png" /> defined by the formula <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730105.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730106.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730107.png" /> is uniquely determined by the double coset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730108.png" /> containing the element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730109.png" />, and the restriction of the induced representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730110.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730111.png" /> is equivalent to the direct sum of the representations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730112.png" />, where the sum is taken over a set of representatives of all possible double cosets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730113.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730114.png" /> (the theorem on the restriction of an induced representation to a subgroup). This theorem can be applied, in particular, to the decomposition of a tensor product of induced representations. The space of operators intertwining a given induced representation admits an explicit description. A representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730115.png" /> of a group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730116.png" /> is equivalent to an induced representation of the type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730117.png" /> for some <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730118.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730119.png" /> if and only if there exists a mapping from the set of subsets of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730120.png" /> to the set of projections in the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730121.png" /> of the representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730122.png" />, such that 1) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730123.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730124.png" />; 2) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730125.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730126.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730127.png" />; 3) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730128.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730129.png" />; and 4) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730130.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730131.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730132.png" /> (such a mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730133.png" /> is called a system of imprimitivity for the representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730134.png" /> with basis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730135.png" />). An induced representation of a finite group can be described directly in terms of moduli over group algebras and can also be defined in categorical terms. A finite group is called monomial if each of its irreducible representations is induced by a one-dimensional representation of some subgroup. Every monomial group is solvable (cf. [[Solvable group|Solvable group]]); every [[Nilpotent group|nilpotent group]] is monomial.
| + | If $ G $ |
| | + | is a finite group, then the inducing representation $ \rho $ |
| | + | is assumed to be finite-dimensional, while the space $ E $ |
| | + | is considered to be the space of all functions $ f $ |
| | + | on $ G $ |
| | + | taking values in $ V $ |
| | + | and satisfying the condition $ f ( hg ) = \rho ( h) f ( g) $. |
| | + | The representation $ {} _ {\{ e \} } U _ {G} ^ \rho $, |
| | + | where $ \rho $ |
| | + | is the identity representation of the identity subgroup $ \{ e \} $, |
| | + | is the right [[Regular representation|regular representation]] of $ G $; |
| | + | the representation $ {} _ {G} U _ {G} ^ \rho $ |
| | + | is equivalent to $ \rho $. |
| | + | The representation $ {} _ {H} U _ {G} ^ \rho $ |
| | + | is equivalent to the representation $ \sigma $ |
| | + | in the space $ W $ |
| | + | of all functions on the homogeneous space $ X = G / H $ |
| | + | with values in $ V $, |
| | + | defined by formulas of the form $ [ \sigma ( g) f ] ( x) = a ( g , x ) f ( xg ) $, |
| | + | where the function $ a $ |
| | + | is defined as follows: If $ s : X \rightarrow G $ |
| | + | is some mapping satisfying the condition $ s ( x) \in x $ |
| | + | for all $ x \in X $, |
| | + | then $ a ( g , x ) = \rho ( h ) $, |
| | + | where $ s ( x) g = hs ( xg ) $ |
| | + | for all $ x \in X $, |
| | + | $ g \in G $. |
| | + | The function $ a $ |
| | + | is a one-dimensional cocycle of the group $ G $ |
| | + | with coefficients in the group of functions on $ X $ |
| | + | with values in the invertible operators in $ V $. |
| | + | If $ \rho _ {1} $ |
| | + | is equivalent to a representation $ \rho _ {2} $, |
| | + | then $ \mathop{\rm Ind} \rho _ {1} $ |
| | + | is equivalent to $ \mathop{\rm Ind} \rho _ {2} $; |
| | + | the representation $ \mathop{\rm Ind} ( \rho \oplus \sigma ) $ |
| | + | is equivalent to $ \mathop{\rm Ind} \rho \oplus \mathop{\rm Ind} \sigma $. |
| | + | If $ K , H $ |
| | + | are subgroups of $ G $, |
| | + | $ K \subset H $ |
| | + | and if $ \rho $ |
| | + | is a representation of $ K $, |
| | + | then the representation of $ G $ |
| | + | induced by the representation $ {} _ {K} U _ {H} ^ \rho $ |
| | + | of $ H $ |
| | + | is equivalent to $ {} _ {K} U _ {G} ^ \rho $( |
| | + | the theorem on the composition of induced representations). If $ \pi , \rho $ |
| | + | are representations of the group $ G $ |
| | + | and the subgroup $ H $, |
| | + | respectively, then the spaces of intertwining operators (cf. [[Intertwining operator|Intertwining operator]]) $ \mathop{\rm Hom} ( \pi , {} _ {H} U _ {G} ^ \rho ) $ |
| | + | and $ \mathop{\rm Hom} ( \pi \mid _ {H} , \rho ) $ |
| | + | are isomorphic, where $ \pi \mid _ {H} $ |
| | + | is the restriction of $ \pi $ |
| | + | to $ H $( |
| | + | Frobenius' reciprocity theorem). In particular, if $ \pi $ |
| | + | and $ \rho $ |
| | + | are irreducible, then $ \pi $ |
| | + | occurs in $ U ^ \rho $ |
| | + | with the same multiplicity as that with which $ \rho $ |
| | + | occurs in $ \pi \mid _ {H} $. |
| | + | The character $ \chi _ \pi $ |
| | + | of the induced representation $ \pi = U ^ \rho $ |
| | + | of the group $ G $ |
| | + | is defined by the formula: |
| | | | |
| − | The definition of an induced representation of a locally compact group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730136.png" /> depends essentially on the choice of the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730137.png" />; for example, one often takes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730138.png" /> to be the space of all continuous functions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730139.png" /> satisfying the condition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730140.png" />, or (if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730141.png" /> is a Lie group) the space of all differentiable functions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730142.png" /> satisfying the same condition. On the other hand, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730143.png" /> be a continuous [[Unitary representation|unitary representation]] of a closed subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730144.png" /> in a Hilbert space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730145.png" /> and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730146.png" /> be a measurable mapping of the locally compact space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730147.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730148.png" /> satisfying the condition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730149.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730150.png" />; let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730151.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730152.png" /> be the moduli of the groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730153.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730154.png" />, respectively (see [[Haar measure|Haar measure]]), and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730155.png" /> be a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730156.png" />-quasi-invariant measure on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730157.png" /> such that
| + | $$ |
| | + | \chi _ \pi ( g) = \ |
| | + | \sum _ |
| | + | {\{ \delta : {\delta y \in H \delta } \} |
| | + | } |
| | + | \chi _ \rho ( \delta g \delta ^ {-} 1 ) , |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730158.png" /></td> </tr></table>
| + | where $ \chi _ \rho $ |
| | + | is the character of the representation $ \rho $ |
| | + | of $ H $ |
| | + | extended by zero to the entire group $ G $ |
| | + | and $ \delta $ |
| | + | runs through the set of representatives of the right cosets of $ G $ |
| | + | by $ H $. |
| | + | Let $ H , K $ |
| | + | be subgroups of $ G $, |
| | + | let $ \rho $ |
| | + | be a representation of $ H $, |
| | + | let $ G _ {g} = K \cap g ^ {-} 1 H g $ |
| | + | for all $ g \in G $ |
| | + | and let $ \pi ^ {g} $ |
| | + | be the representation of $ K $ |
| | + | induced by the representation $ \rho ^ {g} $ |
| | + | of $ G _ {g} $ |
| | + | defined by the formula $ \rho ^ {g} ( x) = \rho ( g x g ^ {-} 1 ) $, |
| | + | $ x \in G _ {g} $. |
| | + | Then $ \pi ^ {g} $ |
| | + | is uniquely determined by the double coset $ H g K $ |
| | + | containing the element $ g $, |
| | + | and the restriction of the induced representation $ {} _ {H} U _ {G} ^ \rho $ |
| | + | to $ K $ |
| | + | is equivalent to the direct sum of the representations $ \pi ^ {g} $, |
| | + | where the sum is taken over a set of representatives of all possible double cosets $ H g K $, |
| | + | $ g \in G $( |
| | + | the theorem on the restriction of an induced representation to a subgroup). This theorem can be applied, in particular, to the decomposition of a tensor product of induced representations. The space of operators intertwining a given induced representation admits an explicit description. A representation $ \pi $ |
| | + | of a group $ G $ |
| | + | is equivalent to an induced representation of the type $ {} _ {H} U _ {G} ^ \rho $ |
| | + | for some $ H $ |
| | + | and $ \rho $ |
| | + | if and only if there exists a mapping from the set of subsets of $ H \setminus G $ |
| | + | to the set of projections in the space $ E $ |
| | + | of the representation $ \pi $, |
| | + | such that 1) $ P (\emptyset) = 0 $, |
| | + | $ P ( H \setminus G ) = 1 $; |
| | + | 2) if $ M , N \subset H \setminus G $ |
| | + | and $ M \cap N = \emptyset $, |
| | + | then $ P ( M \cup N ) = P ( M) + P ( N) $; |
| | + | 3) $ P ( M \cap N ) = P ( M) P ( N) $ |
| | + | for all $ M , N \subset H \setminus G $; |
| | + | and 4) $ P ( M g ) = \pi ^ {-} 1 ( g) P ( M) \pi ( g) $ |
| | + | for all $ M \subset H \setminus G $, |
| | + | $ g \in G $( |
| | + | such a mapping $ P $ |
| | + | is called a system of imprimitivity for the representation $ \pi $ |
| | + | with basis $ H \setminus G $). |
| | + | An induced representation of a finite group can be described directly in terms of moduli over group algebras and can also be defined in categorical terms. A finite group is called monomial if each of its irreducible representations is induced by a one-dimensional representation of some subgroup. Every monomial group is solvable (cf. [[Solvable group|Solvable group]]); every [[Nilpotent group|nilpotent group]] is monomial. |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730159.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730160.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730161.png" />; let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730162.png" /> be the Hilbert space of measurable vector functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730163.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730164.png" /> with values in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730165.png" /> satisfying the condition
| + | The definition of an induced representation of a locally compact group $ G $ |
| | + | depends essentially on the choice of the space $ E $; |
| | + | for example, one often takes $ E $ |
| | + | to be the space of all continuous functions on $ G $ |
| | + | satisfying the condition $ f ( h g ) = \rho ( h) f ( g) $, |
| | + | or (if $ G $ |
| | + | is a Lie group) the space of all differentiable functions on $ G $ |
| | + | satisfying the same condition. On the other hand, let $ \rho $ |
| | + | be a continuous [[Unitary representation|unitary representation]] of a closed subgroup $ H \subset G $ |
| | + | in a Hilbert space $ V $ |
| | + | and let $ s $ |
| | + | be a measurable mapping of the locally compact space $ X = H \setminus G $ |
| | + | into $ G $ |
| | + | satisfying the condition $ s ( x) \in x $ |
| | + | for $ x \in X $; |
| | + | let $ \Delta _ {G} $ |
| | + | and $ \Delta _ {H} $ |
| | + | be the moduli of the groups $ G $ |
| | + | and $ H $, |
| | + | respectively (see [[Haar measure|Haar measure]]), and let $ \nu _ {s} $ |
| | + | be a $ G $- |
| | + | quasi-invariant measure on $ X $ |
| | + | such that |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730166.png" /></td> </tr></table>
| + | $$ |
| | | | |
| − | for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730167.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730168.png" />, and such that the integral
| + | \frac{d \nu _ {s} ( x g ) }{d \nu _ {s} ( x) } |
| | + | = \ |
| | + | \Delta _ {H} ( h ^ {x,g} ) |
| | + | \Delta _ {G} ^ {-} 1 ( h ^ {x,g} ) , |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730169.png" /></td> </tr></table>
| + | where $ s ( x) g = h ^ {x,g} s ( x g ) $ |
| | + | for all $ x \in X $, |
| | + | $ g \in G $; |
| | + | let $ L _ {2} ( G , H , \rho ) $ |
| | + | be the Hilbert space of measurable vector functions $ F $ |
| | + | on $ G $ |
| | + | with values in $ V $ |
| | + | satisfying the condition |
| | | | |
| − | converges; then the continuous unitary representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730170.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730171.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730172.png" /> defined by the formula
| + | $$ |
| | + | F ( h g ) = \ |
| | + | \left [ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730173.png" /></td> </tr></table>
| + | \frac{\Delta _ {H} ( h) }{\Delta _ {G} ( h) } |
| | | | |
| − | for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730174.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730175.png" />, is called the unitary induced representation of the locally compact group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730176.png" />. The majority of results on induced representations of finite groups admit a generalization to the case of unitary induced representations of locally compact groups. Among them are the properties of the representations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730177.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730178.png" />, the connection between induced representations and cocycles on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730179.png" />, the theorem on composition of induced representations, the theorem on the restriction of an induced representation to a subgroup, the formula for the character of an induced representation, the inducibility criterion of a representation, properties of monomial groups, and the Frobenius reciprocity theorem. These admit more or less direct generalizations to the case of unitary induced representations. Induced representations of a locally compact group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730180.png" /> are related to representations of certain generalized group algebras of this group. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730181.png" /> is a Lie group, then the notion of an induced representation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730182.png" /> admits various generalizations, including that of a holomorphically-induced representation, whose representation space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730183.png" /> is the space of functions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730184.png" /> that are analytic in some of the variables, and the notion of a representation in vector bundle cohomology over the homogeneous space of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730185.png" /> (representations in zero cohomology are the induced representations). The notion of an induced representation and its generalizations play a fruitful role in representation theory. In particular, the representations of group extensions can be described in terms of unitary induced representations; the fundamental series of continuous unitary representations of a connected real semi-simple Lie group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730186.png" /> is formed by induced representations, namely, the induced finite-dimensional unitary representations of the Borel subgroup of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730187.png" />; the discrete series of representations of a linear real semi-simple Lie group is realized in certain vector bundle cohomology over the homogeneous spaces of this group; irreducible continuous unitary representations of solvable connected Lie groups of type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730188.png" /> can be described in terms of holomorphically-induced representations [[#References|[7]]]. The operation of forming an induced representation can be generalized to the case of non-unitary representations of locally compact groups, as well as to topological groups that are not locally compact. The analogue of induced representations for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730189.png" />-algebras has been studied [[#References|[6]]]. | + | \right ] ^ {1/2} |
| | + | \cdot \rho ( h) F ( g) |
| | + | $$ |
| | + | |
| | + | for all $ h \in H $, |
| | + | $ g \in G $, |
| | + | and such that the integral |
| | + | |
| | + | $$ |
| | + | \int\limits _ { X } |
| | + | \| F ( s ( x) ) \| _ {V} ^ {2} d \nu _ {s} ( x) |
| | + | $$ |
| | + | |
| | + | converges; then the continuous unitary representation $ \pi $ |
| | + | of $ G $ |
| | + | in $ L _ {2} ( G , H , \rho ) $ |
| | + | defined by the formula |
| | + | |
| | + | $$ |
| | + | [ \pi ( g _ {1} ) F ] ( g) = F ( g g _ {1} ) |
| | + | $$ |
| | + | |
| | + | for all $ g , g _ {1} \in G $, |
| | + | $ F \in L _ {2} ( G , H , \rho ) $, |
| | + | is called the unitary induced representation of the locally compact group $ G $. |
| | + | The majority of results on induced representations of finite groups admit a generalization to the case of unitary induced representations of locally compact groups. Among them are the properties of the representations $ \mathop{\rm Ind} ( \rho _ {1} \oplus \rho _ {2} ) $ |
| | + | and $ \mathop{\rm Ind} ( \rho _ {1} \otimes \rho _ {2} ) $, |
| | + | the connection between induced representations and cocycles on $ G $, |
| | + | the theorem on composition of induced representations, the theorem on the restriction of an induced representation to a subgroup, the formula for the character of an induced representation, the inducibility criterion of a representation, properties of monomial groups, and the Frobenius reciprocity theorem. These admit more or less direct generalizations to the case of unitary induced representations. Induced representations of a locally compact group $ G $ |
| | + | are related to representations of certain generalized group algebras of this group. If $ G $ |
| | + | is a Lie group, then the notion of an induced representation of $ G $ |
| | + | admits various generalizations, including that of a holomorphically-induced representation, whose representation space $ E $ |
| | + | is the space of functions on $ G $ |
| | + | that are analytic in some of the variables, and the notion of a representation in vector bundle cohomology over the homogeneous space of $ G $( |
| | + | representations in zero cohomology are the induced representations). The notion of an induced representation and its generalizations play a fruitful role in representation theory. In particular, the representations of group extensions can be described in terms of unitary induced representations; the fundamental series of continuous unitary representations of a connected real semi-simple Lie group $ G $ |
| | + | is formed by induced representations, namely, the induced finite-dimensional unitary representations of the Borel subgroup of $ G $; |
| | + | the discrete series of representations of a linear real semi-simple Lie group is realized in certain vector bundle cohomology over the homogeneous spaces of this group; irreducible continuous unitary representations of solvable connected Lie groups of type $ I $ |
| | + | can be described in terms of holomorphically-induced representations [[#References|[7]]]. The operation of forming an induced representation can be generalized to the case of non-unitary representations of locally compact groups, as well as to topological groups that are not locally compact. The analogue of induced representations for $ C ^ {*} $- |
| | + | algebras has been studied [[#References|[6]]]. |
| | | | |
| | ====References==== | | ====References==== |
| | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M.A. Naimark, "Theory of group representations" , Springer (1982) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J.-P. Serre, "Linear representations of finite groups" , Springer (1977) (Translated from French)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> G.W. Mackey, "Infinite-dimensional group representations" ''Bull. Amer. Math. Soc.'' , '''69''' (1963) pp. 628–686</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> W. Schmid, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730190.png" /> cohomology and the discrete series" ''Ann. of Math.'' , '''103''' (1976) pp. 375–394</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> M. Rieffel, "Induced representations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730191.png" />-algebras" ''Adv. in Math.'' , '''13''' : 2 (1974) pp. 176–257</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> L. Auslander, B. Konstant, "Polarization and unitary representations of solvable Lie groups" ''Invent. Math.'' , '''14''' : 4 (1971) pp. 255–354</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> A.M. Vershik, I.M. Gel'fand, M.I. Graev, "Representations of the group of diffeomorphisms" ''Russian Math. Surveys'' , '''30''' : 6 (1975) pp. 1–50 ''Uspekhi Mat. Nauk'' , '''30''' : 6 (1975) pp. 3–50</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> M.B. Menskii, "The method of induced representations. Space-time and the concept of a particle" , Moscow (1976) (In Russian)</TD></TR></table> | | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M.A. Naimark, "Theory of group representations" , Springer (1982) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J.-P. Serre, "Linear representations of finite groups" , Springer (1977) (Translated from French)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> G.W. Mackey, "Infinite-dimensional group representations" ''Bull. Amer. Math. Soc.'' , '''69''' (1963) pp. 628–686</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> W. Schmid, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730190.png" /> cohomology and the discrete series" ''Ann. of Math.'' , '''103''' (1976) pp. 375–394</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> M. Rieffel, "Induced representations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050730/i050730191.png" />-algebras" ''Adv. in Math.'' , '''13''' : 2 (1974) pp. 176–257</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> L. Auslander, B. Konstant, "Polarization and unitary representations of solvable Lie groups" ''Invent. Math.'' , '''14''' : 4 (1971) pp. 255–354</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> A.M. Vershik, I.M. Gel'fand, M.I. Graev, "Representations of the group of diffeomorphisms" ''Russian Math. Surveys'' , '''30''' : 6 (1975) pp. 1–50 ''Uspekhi Mat. Nauk'' , '''30''' : 6 (1975) pp. 3–50</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> M.B. Menskii, "The method of induced representations. Space-time and the concept of a particle" , Moscow (1976) (In Russian)</TD></TR></table> |
| − |
| |
| − |
| |
| | | | |
| | ====Comments==== | | ====Comments==== |
| | The "theorem on composition of induced representations" is also called the theorem on induction by stages. | | The "theorem on composition of induced representations" is also called the theorem on induction by stages. |
A representation $ \pi $
of a locally compact group $ G $
induced by a representation $ \rho $
of a closed subgroup $ H $(
cf. Representation of a group). More precisely, it is a representation $ \pi $
of $ G $
in some space $ E $
of functions $ f $
on $ G $
taking values in the space $ V $
of the representation $ \rho $
and satisfying the condition $ f ( hg ) = \rho ( h) f ( g ) $
for all $ g \in G $,
$ h \in H $,
where $ [ \pi ( g _ {1} ) f ] ( g ) = f ( g g _ {1} ) $
for all $ f \in E $,
$ g , g _ {1} \in G $.
The induced representation $ \pi $
is usually denoted by $ \mathop{\rm Ind} \rho $,
$ \mathop{\rm Ind} _ {H} ^ {G} \rho $,
$ U ^ \rho $,
$ {} _ {H} U ^ \rho $,
or $ {} _ {H} U _ {G} ^ \rho $.
The operation of constructing an induced representation is the simplest and most important stage in the construction of representations of more complicated groups by starting from representations of simpler groups, and for a wide class of groups a complete description of the irreducible representations can be given in terms of induced representations or their generalizations.
If $ G $
is a finite group, then the inducing representation $ \rho $
is assumed to be finite-dimensional, while the space $ E $
is considered to be the space of all functions $ f $
on $ G $
taking values in $ V $
and satisfying the condition $ f ( hg ) = \rho ( h) f ( g) $.
The representation $ {} _ {\{ e \} } U _ {G} ^ \rho $,
where $ \rho $
is the identity representation of the identity subgroup $ \{ e \} $,
is the right regular representation of $ G $;
the representation $ {} _ {G} U _ {G} ^ \rho $
is equivalent to $ \rho $.
The representation $ {} _ {H} U _ {G} ^ \rho $
is equivalent to the representation $ \sigma $
in the space $ W $
of all functions on the homogeneous space $ X = G / H $
with values in $ V $,
defined by formulas of the form $ [ \sigma ( g) f ] ( x) = a ( g , x ) f ( xg ) $,
where the function $ a $
is defined as follows: If $ s : X \rightarrow G $
is some mapping satisfying the condition $ s ( x) \in x $
for all $ x \in X $,
then $ a ( g , x ) = \rho ( h ) $,
where $ s ( x) g = hs ( xg ) $
for all $ x \in X $,
$ g \in G $.
The function $ a $
is a one-dimensional cocycle of the group $ G $
with coefficients in the group of functions on $ X $
with values in the invertible operators in $ V $.
If $ \rho _ {1} $
is equivalent to a representation $ \rho _ {2} $,
then $ \mathop{\rm Ind} \rho _ {1} $
is equivalent to $ \mathop{\rm Ind} \rho _ {2} $;
the representation $ \mathop{\rm Ind} ( \rho \oplus \sigma ) $
is equivalent to $ \mathop{\rm Ind} \rho \oplus \mathop{\rm Ind} \sigma $.
If $ K , H $
are subgroups of $ G $,
$ K \subset H $
and if $ \rho $
is a representation of $ K $,
then the representation of $ G $
induced by the representation $ {} _ {K} U _ {H} ^ \rho $
of $ H $
is equivalent to $ {} _ {K} U _ {G} ^ \rho $(
the theorem on the composition of induced representations). If $ \pi , \rho $
are representations of the group $ G $
and the subgroup $ H $,
respectively, then the spaces of intertwining operators (cf. Intertwining operator) $ \mathop{\rm Hom} ( \pi , {} _ {H} U _ {G} ^ \rho ) $
and $ \mathop{\rm Hom} ( \pi \mid _ {H} , \rho ) $
are isomorphic, where $ \pi \mid _ {H} $
is the restriction of $ \pi $
to $ H $(
Frobenius' reciprocity theorem). In particular, if $ \pi $
and $ \rho $
are irreducible, then $ \pi $
occurs in $ U ^ \rho $
with the same multiplicity as that with which $ \rho $
occurs in $ \pi \mid _ {H} $.
The character $ \chi _ \pi $
of the induced representation $ \pi = U ^ \rho $
of the group $ G $
is defined by the formula:
$$
\chi _ \pi ( g) = \
\sum _
{\{ \delta : {\delta y \in H \delta } \}
}
\chi _ \rho ( \delta g \delta ^ {-} 1 ) ,
$$
where $ \chi _ \rho $
is the character of the representation $ \rho $
of $ H $
extended by zero to the entire group $ G $
and $ \delta $
runs through the set of representatives of the right cosets of $ G $
by $ H $.
Let $ H , K $
be subgroups of $ G $,
let $ \rho $
be a representation of $ H $,
let $ G _ {g} = K \cap g ^ {-} 1 H g $
for all $ g \in G $
and let $ \pi ^ {g} $
be the representation of $ K $
induced by the representation $ \rho ^ {g} $
of $ G _ {g} $
defined by the formula $ \rho ^ {g} ( x) = \rho ( g x g ^ {-} 1 ) $,
$ x \in G _ {g} $.
Then $ \pi ^ {g} $
is uniquely determined by the double coset $ H g K $
containing the element $ g $,
and the restriction of the induced representation $ {} _ {H} U _ {G} ^ \rho $
to $ K $
is equivalent to the direct sum of the representations $ \pi ^ {g} $,
where the sum is taken over a set of representatives of all possible double cosets $ H g K $,
$ g \in G $(
the theorem on the restriction of an induced representation to a subgroup). This theorem can be applied, in particular, to the decomposition of a tensor product of induced representations. The space of operators intertwining a given induced representation admits an explicit description. A representation $ \pi $
of a group $ G $
is equivalent to an induced representation of the type $ {} _ {H} U _ {G} ^ \rho $
for some $ H $
and $ \rho $
if and only if there exists a mapping from the set of subsets of $ H \setminus G $
to the set of projections in the space $ E $
of the representation $ \pi $,
such that 1) $ P (\emptyset) = 0 $,
$ P ( H \setminus G ) = 1 $;
2) if $ M , N \subset H \setminus G $
and $ M \cap N = \emptyset $,
then $ P ( M \cup N ) = P ( M) + P ( N) $;
3) $ P ( M \cap N ) = P ( M) P ( N) $
for all $ M , N \subset H \setminus G $;
and 4) $ P ( M g ) = \pi ^ {-} 1 ( g) P ( M) \pi ( g) $
for all $ M \subset H \setminus G $,
$ g \in G $(
such a mapping $ P $
is called a system of imprimitivity for the representation $ \pi $
with basis $ H \setminus G $).
An induced representation of a finite group can be described directly in terms of moduli over group algebras and can also be defined in categorical terms. A finite group is called monomial if each of its irreducible representations is induced by a one-dimensional representation of some subgroup. Every monomial group is solvable (cf. Solvable group); every nilpotent group is monomial.
The definition of an induced representation of a locally compact group $ G $
depends essentially on the choice of the space $ E $;
for example, one often takes $ E $
to be the space of all continuous functions on $ G $
satisfying the condition $ f ( h g ) = \rho ( h) f ( g) $,
or (if $ G $
is a Lie group) the space of all differentiable functions on $ G $
satisfying the same condition. On the other hand, let $ \rho $
be a continuous unitary representation of a closed subgroup $ H \subset G $
in a Hilbert space $ V $
and let $ s $
be a measurable mapping of the locally compact space $ X = H \setminus G $
into $ G $
satisfying the condition $ s ( x) \in x $
for $ x \in X $;
let $ \Delta _ {G} $
and $ \Delta _ {H} $
be the moduli of the groups $ G $
and $ H $,
respectively (see Haar measure), and let $ \nu _ {s} $
be a $ G $-
quasi-invariant measure on $ X $
such that
$$
\frac{d \nu _ {s} ( x g ) }{d \nu _ {s} ( x) }
= \
\Delta _ {H} ( h ^ {x,g} )
\Delta _ {G} ^ {-} 1 ( h ^ {x,g} ) ,
$$
where $ s ( x) g = h ^ {x,g} s ( x g ) $
for all $ x \in X $,
$ g \in G $;
let $ L _ {2} ( G , H , \rho ) $
be the Hilbert space of measurable vector functions $ F $
on $ G $
with values in $ V $
satisfying the condition
$$
F ( h g ) = \
\left [
\frac{\Delta _ {H} ( h) }{\Delta _ {G} ( h) }
\right ] ^ {1/2}
\cdot \rho ( h) F ( g)
$$
for all $ h \in H $,
$ g \in G $,
and such that the integral
$$
\int\limits _ { X }
\| F ( s ( x) ) \| _ {V} ^ {2} d \nu _ {s} ( x)
$$
converges; then the continuous unitary representation $ \pi $
of $ G $
in $ L _ {2} ( G , H , \rho ) $
defined by the formula
$$
[ \pi ( g _ {1} ) F ] ( g) = F ( g g _ {1} )
$$
for all $ g , g _ {1} \in G $,
$ F \in L _ {2} ( G , H , \rho ) $,
is called the unitary induced representation of the locally compact group $ G $.
The majority of results on induced representations of finite groups admit a generalization to the case of unitary induced representations of locally compact groups. Among them are the properties of the representations $ \mathop{\rm Ind} ( \rho _ {1} \oplus \rho _ {2} ) $
and $ \mathop{\rm Ind} ( \rho _ {1} \otimes \rho _ {2} ) $,
the connection between induced representations and cocycles on $ G $,
the theorem on composition of induced representations, the theorem on the restriction of an induced representation to a subgroup, the formula for the character of an induced representation, the inducibility criterion of a representation, properties of monomial groups, and the Frobenius reciprocity theorem. These admit more or less direct generalizations to the case of unitary induced representations. Induced representations of a locally compact group $ G $
are related to representations of certain generalized group algebras of this group. If $ G $
is a Lie group, then the notion of an induced representation of $ G $
admits various generalizations, including that of a holomorphically-induced representation, whose representation space $ E $
is the space of functions on $ G $
that are analytic in some of the variables, and the notion of a representation in vector bundle cohomology over the homogeneous space of $ G $(
representations in zero cohomology are the induced representations). The notion of an induced representation and its generalizations play a fruitful role in representation theory. In particular, the representations of group extensions can be described in terms of unitary induced representations; the fundamental series of continuous unitary representations of a connected real semi-simple Lie group $ G $
is formed by induced representations, namely, the induced finite-dimensional unitary representations of the Borel subgroup of $ G $;
the discrete series of representations of a linear real semi-simple Lie group is realized in certain vector bundle cohomology over the homogeneous spaces of this group; irreducible continuous unitary representations of solvable connected Lie groups of type $ I $
can be described in terms of holomorphically-induced representations [7]. The operation of forming an induced representation can be generalized to the case of non-unitary representations of locally compact groups, as well as to topological groups that are not locally compact. The analogue of induced representations for $ C ^ {*} $-
algebras has been studied [6].
References
| [1] | A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian) |
| [2] | M.A. Naimark, "Theory of group representations" , Springer (1982) (Translated from Russian) |
| [3] | J.-P. Serre, "Linear representations of finite groups" , Springer (1977) (Translated from French) |
| [4] | G.W. Mackey, "Infinite-dimensional group representations" Bull. Amer. Math. Soc. , 69 (1963) pp. 628–686 |
| [5] | W. Schmid, "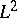 cohomology and the discrete series" Ann. of Math. , 103 (1976) pp. 375–394 cohomology and the discrete series" Ann. of Math. , 103 (1976) pp. 375–394 |
| [6] | M. Rieffel, "Induced representations of 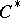 -algebras" Adv. in Math. , 13 : 2 (1974) pp. 176–257 -algebras" Adv. in Math. , 13 : 2 (1974) pp. 176–257 |
| [7] | L. Auslander, B. Konstant, "Polarization and unitary representations of solvable Lie groups" Invent. Math. , 14 : 4 (1971) pp. 255–354 |
| [8] | A.M. Vershik, I.M. Gel'fand, M.I. Graev, "Representations of the group of diffeomorphisms" Russian Math. Surveys , 30 : 6 (1975) pp. 1–50 Uspekhi Mat. Nauk , 30 : 6 (1975) pp. 3–50 |
| [9] | M.B. Menskii, "The method of induced representations. Space-time and the concept of a particle" , Moscow (1976) (In Russian) |
The "theorem on composition of induced representations" is also called the theorem on induction by stages.
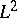 cohomology and the discrete series" Ann. of Math. , 103 (1976) pp. 375–394
cohomology and the discrete series" Ann. of Math. , 103 (1976) pp. 375–394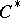 -algebras" Adv. in Math. , 13 : 2 (1974) pp. 176–257
-algebras" Adv. in Math. , 13 : 2 (1974) pp. 176–257