Difference between revisions of "Frobenius theorem"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | f0417901.png | ||
| + | $#A+1 = 42 n = 2 | ||
| + | $#C+1 = 42 : ~/encyclopedia/old_files/data/F041/F.0401790 Frobenius theorem | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
A theorem that describes all finite-dimensional associative real algebras without divisors of zero; it was proved by G. Frobenius [[#References|[1]]]. Frobenius' theorem asserts that: | A theorem that describes all finite-dimensional associative real algebras without divisors of zero; it was proved by G. Frobenius [[#References|[1]]]. Frobenius' theorem asserts that: | ||
| Line 13: | Line 25: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> G. Frobenius, "Ueber lineare Substitutionen and bilineare Formen" ''J. Reine Angew. Math.'' , '''84''' (1878) pp. 1–63</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) (Translated from Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> G. Frobenius, "Ueber lineare Substitutionen and bilineare Formen" ''J. Reine Angew. Math.'' , '''84''' (1878) pp. 1–63</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) (Translated from Russian)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| Line 25: | Line 35: | ||
i) The [[Perron–Frobenius theorem|Perron–Frobenius theorem]] on eigen values of non-negative matrices. | i) The [[Perron–Frobenius theorem|Perron–Frobenius theorem]] on eigen values of non-negative matrices. | ||
| − | ii) The following result in finite group theory. Let | + | ii) The following result in finite group theory. Let |
| + | be a subgroup of a finite group G | ||
| + | such that $ x H x ^ {-} 1 \cap H = \{ e \} $ | ||
| + | for x \in G \setminus H . | ||
| + | Then $ G \setminus \cup _ {x} x ( H \setminus \{ e \} ) x ^ {-} 1 = N $ | ||
| + | is a normal subgroup and $ G = HN $. | ||
| + | A generalization of this theorem is known as the Frobenius–Wielandt theorem. | ||
| − | iii) A theorem on normal | + | iii) A theorem on normal p - |
| + | complements, cf. [[Normal p-complement|Normal p - | ||
| + | complement]]. | ||
| − | iv) A result on Abelian varieties. Let | + | iv) A result on Abelian varieties. Let A |
| + | be an [[Abelian variety|Abelian variety]] over \mathbf C , | ||
| + | D | ||
| + | a [[Divisor|divisor]] on A | ||
| + | and \widehat{A} | ||
| + | the [[Picard variety|Picard variety]] of A . | ||
| + | Let $ \psi _ {D} : A \rightarrow \widehat{A} $ | ||
| + | be defined by a \mapsto | ||
| + | the linear equivalence class of the divisor ( D _ {a} ) - D , | ||
| + | where D _ {a} | ||
| + | is the image of D | ||
| + | under the translation A \rightarrow A , | ||
| + | b \mapsto a+ b . | ||
| + | There are elements a _ {1} \dots a _ {n} | ||
| + | such that the intersection (product) D _ {a _ {1} } \cdot \dots \cdot D _ {a _ {n} } | ||
| + | is defined ( $ n = \mathop{\rm dim} A $). | ||
| + | Let n _ {D} | ||
| + | be the degree of the zero-cycle D _ {a _ {1} } \cdot \dots \cdot D _ {a _ {n} } . | ||
| + | Then the degree of the mapping \psi _ {D} | ||
| + | is equal to ( n! ) ^ {-} 1 n _ {D} ( | ||
| + | Frobenius' theorem). | ||
v) The Frobenius reciprocity theorem for induced representations; cf. [[Induced representation|Induced representation]]. | v) The Frobenius reciprocity theorem for induced representations; cf. [[Induced representation|Induced representation]]. | ||
| − | vi) The Frobenius–Schur theorem. Let | + | vi) The Frobenius–Schur theorem. Let K |
| + | be an algebraically closed field, A | ||
| + | an algebra over K | ||
| + | and let M _ {1} \dots M _ {k} | ||
| + | be a set of non-isomorphic irreducible left A - | ||
| + | modules of dimensions n _ {r} | ||
| + | over K , | ||
| + | $ r = 1 \dots k $. | ||
| + | Let $ \phi _ {r} : A \rightarrow \mathop{\rm End} _ {K} ( M _ {r} ) $ | ||
| + | be the corresponding representation with entry functions $ f _ {ij} ^ { r } $; | ||
| + | 1 \leq i , j \leq n _ {r} , | ||
| + | $ r = 1 \dots k $. | ||
| + | Then these coordinate functions $ f _ {ij} ^ { r } $ | ||
| + | are linearly independent over K . | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> M. Kervaire, "Non-parallelizability of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041790/f04179043.png" />-sphere for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041790/f04179044.png" />" ''Proc. Nat. Acad. Sc. USA'' , '''44''' (1958) pp. 280–283</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.W. Milnor, "Some consequences of a theorem of Bott" ''Ann. of Math.'' , '''68''' (1958) pp. 444–449</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962) pp. §90, §41</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> M. Kervaire, "Non-parallelizability of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041790/f04179043.png" />-sphere for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041790/f04179044.png" />" ''Proc. Nat. Acad. Sc. USA'' , '''44''' (1958) pp. 280–283</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.W. Milnor, "Some consequences of a theorem of Bott" ''Ann. of Math.'' , '''68''' (1958) pp. 444–449</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962) pp. §90, §41</TD></TR></table> | ||
Latest revision as of 19:40, 5 June 2020
A theorem that describes all finite-dimensional associative real algebras without divisors of zero; it was proved by G. Frobenius [1]. Frobenius' theorem asserts that:
1) the field of real numbers and the field of complex numbers are the only finite-dimensional real associative-commutative algebras without divisors of zero; and
2) the skew-field of quaternions is the only finite-dimensional real associative, but not commutative, algebra without divisors of zero.
There is also a description of all finite-dimensional alternative algebras without divisors of zero:
3) the Cayley algebra is the only finite-dimensional real alternative, but not associative, algebra without divisors of zero.
The conjunction of these three assertions is called the generalized Frobenius theorem. All the algebras that appear in the statement of the theorem turn out to be algebras with unique division and with a one. The Frobenius theorem cannot be generalized to the case of non-alternative algebras. It has been proved, however, that the dimension of any finite-dimensional real algebra without divisors of zero can only take the values 1, 2, 4, or 8.
References
| [1] | G. Frobenius, "Ueber lineare Substitutionen and bilineare Formen" J. Reine Angew. Math. , 84 (1878) pp. 1–63 |
| [2] | A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) (Translated from Russian) |
Comments
See also Alternative rings and algebras.
The theorem that the only possible division algebras with real coefficients are the reals, the complexes, the quaternions, and the Cayley numbers (or octonians) is due to M. Kervaire [a1] and J. Milnor [a2]. Its proof relies on topological considerations, notably results of R. Bott.
Besides the result mentioned above and the Frobenius theorem on Pfaffian systems, there are a number of other results which (sometimes) go by the name Frobenius theorem. Some of them are:
i) The Perron–Frobenius theorem on eigen values of non-negative matrices.
ii) The following result in finite group theory. Let H be a subgroup of a finite group G such that x H x ^ {-} 1 \cap H = \{ e \} for x \in G \setminus H . Then G \setminus \cup _ {x} x ( H \setminus \{ e \} ) x ^ {-} 1 = N is a normal subgroup and G = HN . A generalization of this theorem is known as the Frobenius–Wielandt theorem.
iii) A theorem on normal p - complements, cf. Normal p - complement.
iv) A result on Abelian varieties. Let A be an Abelian variety over \mathbf C , D a divisor on A and \widehat{A} the Picard variety of A . Let \psi _ {D} : A \rightarrow \widehat{A} be defined by a \mapsto the linear equivalence class of the divisor ( D _ {a} ) - D , where D _ {a} is the image of D under the translation A \rightarrow A , b \mapsto a+ b . There are elements a _ {1} \dots a _ {n} such that the intersection (product) D _ {a _ {1} } \cdot \dots \cdot D _ {a _ {n} } is defined ( n = \mathop{\rm dim} A ). Let n _ {D} be the degree of the zero-cycle D _ {a _ {1} } \cdot \dots \cdot D _ {a _ {n} } . Then the degree of the mapping \psi _ {D} is equal to ( n! ) ^ {-} 1 n _ {D} ( Frobenius' theorem).
v) The Frobenius reciprocity theorem for induced representations; cf. Induced representation.
vi) The Frobenius–Schur theorem. Let K be an algebraically closed field, A an algebra over K and let M _ {1} \dots M _ {k} be a set of non-isomorphic irreducible left A - modules of dimensions n _ {r} over K , r = 1 \dots k . Let \phi _ {r} : A \rightarrow \mathop{\rm End} _ {K} ( M _ {r} ) be the corresponding representation with entry functions f _ {ij} ^ { r } ; 1 \leq i , j \leq n _ {r} , r = 1 \dots k . Then these coordinate functions f _ {ij} ^ { r } are linearly independent over K .
References
| [a1] | M. Kervaire, "Non-parallelizability of the  -sphere for -sphere for 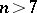 " Proc. Nat. Acad. Sc. USA , 44 (1958) pp. 280–283 " Proc. Nat. Acad. Sc. USA , 44 (1958) pp. 280–283 |
| [a2] | J.W. Milnor, "Some consequences of a theorem of Bott" Ann. of Math. , 68 (1958) pp. 444–449 |
| [a3] | C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962) pp. §90, §41 |
Frobenius theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Frobenius_theorem&oldid=46994