Difference between revisions of "Fresnel integrals"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | f0417201.png | ||
| + | $#A+1 = 26 n = 0 | ||
| + | $#C+1 = 26 : ~/encyclopedia/old_files/data/F041/F.0401720 Fresnel integrals | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
The special functions | The special functions | ||
| − | + | $$ | |
| + | C ( x) = { | ||
| + | \frac{1}{\sqrt {2 \pi } } | ||
| + | } | ||
| + | \int\limits _ { 0 } ^ { {x ^ {2}} } | ||
| + | |||
| + | \frac{\cos t }{\sqrt t } | ||
| + | dt = \ | ||
| + | \sqrt { | ||
| + | \frac{2} \pi | ||
| + | } | ||
| + | \int\limits _ { 0 } ^ { x } | ||
| + | \cos t ^ {2} dt, | ||
| + | $$ | ||
| − | + | $$ | |
| + | S ( x) = { | ||
| + | \frac{1}{\sqrt {2 \pi } } | ||
| + | } \int\limits _ { 0 } ^ { {x } | ||
| + | ^ {2} } | ||
| + | \frac{\sin t }{\sqrt t } | ||
| + | dt = \sqrt { | ||
| + | \frac{2} \pi | ||
| + | } \int\limits _ { 0 } ^ { x } \sin t ^ {2} dt; | ||
| + | $$ | ||
| − | + | $$ | |
| + | \lim\limits _ {x \rightarrow + \infty } C ( x) = \lim\limits _ {x \rightarrow + \infty } S ( x) = { | ||
| + | \frac{1}{2} | ||
| + | } . | ||
| + | $$ | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/f041720a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/f041720a.gif" /> | ||
| Line 13: | Line 51: | ||
The Fresnel integrals can be represented in the form of the series | The Fresnel integrals can be represented in the form of the series | ||
| − | + | $$ | |
| + | C ( x) = \sqrt { | ||
| + | \frac{2} \pi | ||
| + | } x | ||
| + | \sum _ {k = 0 } ^ \infty | ||
| + | |||
| + | \frac{(- 1) ^ {k} x ^ {4k} }{( 2k)! ( 4k + 1) } | ||
| + | , | ||
| + | $$ | ||
| − | + | $$ | |
| + | S ( x) = \sqrt { | ||
| + | \frac{2} \pi | ||
| + | } x \sum _ {k = 0 } ^ \infty | ||
| + | \frac{(- 1) ^ {k} x ^ {2 ( 2 k + 1) } }{( 2k + 1)! ( 4k + 3) } | ||
| + | . | ||
| + | $$ | ||
| − | An asymptotic representation for large | + | An asymptotic representation for large $ x $ |
| + | is: | ||
| − | + | $$ | |
| + | C ( x) = { | ||
| + | \frac{1}{2} | ||
| + | } + | ||
| − | + | \frac{1}{\sqrt {2 \pi } x } | |
| + | \ | ||
| + | \sin x ^ {2} + O | ||
| + | \left ( | ||
| + | \frac{1}{x ^ {2} } | ||
| + | \right ) , | ||
| + | $$ | ||
| − | + | $$ | |
| + | S ( x) = { | ||
| + | \frac{1}{2} | ||
| + | } - | ||
| + | \frac{1}{\sqrt {2 \pi } x } | ||
| + | \cos | ||
| + | x ^ {2} + O \left ( | ||
| + | \frac{1}{x ^ {2} } | ||
| + | \right ) . | ||
| + | $$ | ||
| − | + | In a rectangular coordinate system $ ( x, y) $ | |
| + | the projections of the curve | ||
| − | + | $$ | |
| + | x = t,\ \ | ||
| + | y = C \left ( { | ||
| + | \frac \pi {2} | ||
| + | } t ^ {2} \right ) ,\ \ | ||
| + | z = S \left ( { | ||
| + | \frac \pi {2} | ||
| + | } t ^ {2} \right ) , | ||
| + | $$ | ||
| + | |||
| + | where $ t $ | ||
| + | is a real parameter, onto the coordinate planes are the [[Cornu spiral|Cornu spiral]] and the curves $ y = C ( \pi t ^ {2} /2) $, | ||
| + | $ z = S ( \pi t ^ {2} /2) $( | ||
| + | see Fig. b). $ x $ | ||
| + | $ S( x) $ | ||
| + | $ C( x) $ | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/f041720b.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/f041720b.gif" /> | ||
| Line 35: | Line 122: | ||
The generalized Fresnel integrals (see [[#References|[1]]]) are functions of the form | The generalized Fresnel integrals (see [[#References|[1]]]) are functions of the form | ||
| − | + | $$ | |
| + | C ( x, \alpha ) = \ | ||
| + | \int\limits _ { x } ^ \infty | ||
| + | t ^ {\alpha - 1 } \ | ||
| + | \cos t dt, | ||
| + | $$ | ||
| − | + | $$ | |
| + | S ( x, \alpha ) = \int\limits _ { x } ^ \infty t ^ {\alpha - 1 } \sin t dt. | ||
| + | $$ | ||
The Fresnel integrals are related to the generalized Fresnel integrals as follows: | The Fresnel integrals are related to the generalized Fresnel integrals as follows: | ||
| − | + | $$ | |
| + | C ( x) = { | ||
| + | \frac{1}{2} | ||
| + | } - | ||
| − | + | \frac{1}{\sqrt {2 \pi } } | |
| + | |||
| + | C \left ( x ^ {2} , { | ||
| + | \frac{1}{2} | ||
| + | } \right ) ; | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | S ( x) = { | ||
| + | \frac{1}{2} | ||
| + | } - | ||
| + | \frac{1}{\sqrt {2 \pi } } | ||
| + | S \left ( x ^ {2} , { | ||
| + | \frac{1}{2} | ||
| + | } \right ) . | ||
| + | $$ | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Bateman (ed.) A. Erdélyi (ed.) et al. (ed.) , ''Higher transcendental functions'' , '''2. Bessel functions, parabolic cylinder functions, orthogonal polynomials''' , McGraw-Hill (1953)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> E. Jahnke, F. Emde, "Tables of functions with formulae and curves" , Dover, reprint (1945) (Translated from German)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Bateman (ed.) A. Erdélyi (ed.) et al. (ed.) , ''Higher transcendental functions'' , '''2. Bessel functions, parabolic cylinder functions, orthogonal polynomials''' , McGraw-Hill (1953)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> E. Jahnke, F. Emde, "Tables of functions with formulae and curves" , Dover, reprint (1945) (Translated from German)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
A word of warning. There are different normalizations in use for the Fresnel integrals. E.g., in [[#References|[a3]]] they are defined as | A word of warning. There are different normalizations in use for the Fresnel integrals. E.g., in [[#References|[a3]]] they are defined as | ||
| − | + | $$ | |
| + | C _ {1} ( z) = \int\limits _ { 0 } ^ { z } | ||
| + | \cos | ||
| + | \frac{\pi t ^ {2} }{2} | ||
| + | d t ,\ S _ {1} ( z) = \ | ||
| + | \int\limits _ { 0 } ^ { z } \sin | ||
| + | \frac{\pi t ^ {2} }{2} | ||
| + | d t , | ||
| + | $$ | ||
so that | so that | ||
| − | + | $$ | |
| + | C _ {1} ( z) = C \left ( \sqrt { | ||
| + | \frac \pi {2} | ||
| + | } z \right ) \ \ | ||
| + | \textrm{ and } \ \ | ||
| + | S _ {1} ( z) = S \left ( \sqrt { | ||
| + | \frac \pi {2} | ||
| + | } z \right ) . | ||
| + | $$ | ||
| + | |||
| + | The Fresnel integrals defined in the article are related to the [[Probability integral|probability integral]] for a complex argument $ z = \sqrt i x $, | ||
| + | |||
| + | $$ | ||
| + | \Phi ( z) = | ||
| + | \frac{2}{\sqrt \pi } | ||
| − | + | \int\limits _ { 0 } ^ { z } e ^ {- t ^ {2} } d t | |
| + | $$ | ||
| − | + | (integration along the line $ \mathop{\rm Re} z = \mathop{\rm Im} z $), | |
| + | by | ||
| − | + | $$ | |
| − | + | \frac{\Phi ( \sqrt i x ) }{\sqrt i } | |
| + | = \ | ||
| + | \sqrt 2 C ( x) - i \sqrt 2 S ( x) . | ||
| + | $$ | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Segun, M. Abramowitz, "Handbook of mathematical functions" , ''Appl. Math. Ser.'' , '''55''' , Nat. Bur. Standards (1970)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Spanier, K.B. Oldham, "An atlas of functions" , Hemisphere & Springer (1987) pp. Chapt. 39</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> N.N. Lebedev, "Special functions and their applications" , Dover, reprint (1972) pp. 21–33 (Translated from Russian)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Segun, M. Abramowitz, "Handbook of mathematical functions" , ''Appl. Math. Ser.'' , '''55''' , Nat. Bur. Standards (1970)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Spanier, K.B. Oldham, "An atlas of functions" , Hemisphere & Springer (1987) pp. Chapt. 39</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> N.N. Lebedev, "Special functions and their applications" , Dover, reprint (1972) pp. 21–33 (Translated from Russian)</TD></TR></table> | ||
Latest revision as of 19:40, 5 June 2020
The special functions
$$ C ( x) = { \frac{1}{\sqrt {2 \pi } } } \int\limits _ { 0 } ^ { {x ^ {2}} } \frac{\cos t }{\sqrt t } dt = \ \sqrt { \frac{2} \pi } \int\limits _ { 0 } ^ { x } \cos t ^ {2} dt, $$
$$ S ( x) = { \frac{1}{\sqrt {2 \pi } } } \int\limits _ { 0 } ^ { {x } ^ {2} } \frac{\sin t }{\sqrt t } dt = \sqrt { \frac{2} \pi } \int\limits _ { 0 } ^ { x } \sin t ^ {2} dt; $$
$$ \lim\limits _ {x \rightarrow + \infty } C ( x) = \lim\limits _ {x \rightarrow + \infty } S ( x) = { \frac{1}{2} } . $$
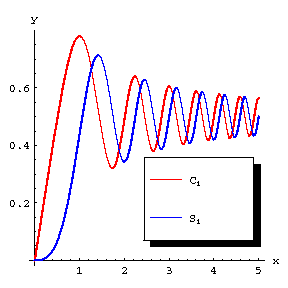
Figure: f041720a
The Fresnel integrals can be represented in the form of the series
$$ C ( x) = \sqrt { \frac{2} \pi } x \sum _ {k = 0 } ^ \infty \frac{(- 1) ^ {k} x ^ {4k} }{( 2k)! ( 4k + 1) } , $$
$$ S ( x) = \sqrt { \frac{2} \pi } x \sum _ {k = 0 } ^ \infty \frac{(- 1) ^ {k} x ^ {2 ( 2 k + 1) } }{( 2k + 1)! ( 4k + 3) } . $$
An asymptotic representation for large $ x $ is:
$$ C ( x) = { \frac{1}{2} } + \frac{1}{\sqrt {2 \pi } x } \ \sin x ^ {2} + O \left ( \frac{1}{x ^ {2} } \right ) , $$
$$ S ( x) = { \frac{1}{2} } - \frac{1}{\sqrt {2 \pi } x } \cos x ^ {2} + O \left ( \frac{1}{x ^ {2} } \right ) . $$
In a rectangular coordinate system $ ( x, y) $ the projections of the curve
$$ x = t,\ \ y = C \left ( { \frac \pi {2} } t ^ {2} \right ) ,\ \ z = S \left ( { \frac \pi {2} } t ^ {2} \right ) , $$
where $ t $ is a real parameter, onto the coordinate planes are the Cornu spiral and the curves $ y = C ( \pi t ^ {2} /2) $, $ z = S ( \pi t ^ {2} /2) $( see Fig. b). $ x $ $ S( x) $ $ C( x) $

Figure: f041720b
The generalized Fresnel integrals (see [1]) are functions of the form
$$ C ( x, \alpha ) = \ \int\limits _ { x } ^ \infty t ^ {\alpha - 1 } \ \cos t dt, $$
$$ S ( x, \alpha ) = \int\limits _ { x } ^ \infty t ^ {\alpha - 1 } \sin t dt. $$
The Fresnel integrals are related to the generalized Fresnel integrals as follows:
$$ C ( x) = { \frac{1}{2} } - \frac{1}{\sqrt {2 \pi } } C \left ( x ^ {2} , { \frac{1}{2} } \right ) ; $$
$$ S ( x) = { \frac{1}{2} } - \frac{1}{\sqrt {2 \pi } } S \left ( x ^ {2} , { \frac{1}{2} } \right ) . $$
References
| [1] | H. Bateman (ed.) A. Erdélyi (ed.) et al. (ed.) , Higher transcendental functions , 2. Bessel functions, parabolic cylinder functions, orthogonal polynomials , McGraw-Hill (1953) |
| [2] | E. Jahnke, F. Emde, "Tables of functions with formulae and curves" , Dover, reprint (1945) (Translated from German) |
Comments
A word of warning. There are different normalizations in use for the Fresnel integrals. E.g., in [a3] they are defined as
$$ C _ {1} ( z) = \int\limits _ { 0 } ^ { z } \cos \frac{\pi t ^ {2} }{2} d t ,\ S _ {1} ( z) = \ \int\limits _ { 0 } ^ { z } \sin \frac{\pi t ^ {2} }{2} d t , $$
so that
$$ C _ {1} ( z) = C \left ( \sqrt { \frac \pi {2} } z \right ) \ \ \textrm{ and } \ \ S _ {1} ( z) = S \left ( \sqrt { \frac \pi {2} } z \right ) . $$
The Fresnel integrals defined in the article are related to the probability integral for a complex argument $ z = \sqrt i x $,
$$ \Phi ( z) = \frac{2}{\sqrt \pi } \int\limits _ { 0 } ^ { z } e ^ {- t ^ {2} } d t $$
(integration along the line $ \mathop{\rm Re} z = \mathop{\rm Im} z $), by
$$ \frac{\Phi ( \sqrt i x ) }{\sqrt i } = \ \sqrt 2 C ( x) - i \sqrt 2 S ( x) . $$
References
| [a1] | A. Segun, M. Abramowitz, "Handbook of mathematical functions" , Appl. Math. Ser. , 55 , Nat. Bur. Standards (1970) |
| [a2] | J. Spanier, K.B. Oldham, "An atlas of functions" , Hemisphere & Springer (1987) pp. Chapt. 39 |
| [a3] | N.N. Lebedev, "Special functions and their applications" , Dover, reprint (1972) pp. 21–33 (Translated from Russian) |
Fresnel integrals. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fresnel_integrals&oldid=46990