Cornu spiral
clothoid
A transcendental plane curve (see Fig.) whose natural equation is
$$r=\frac as,$$
where $r$ is the radius of curvature, $a=\text{const}$ and $s$ is the arc length. It can be parametrized by the Fresnel integrals
$$x=\int\limits_0^t\cos\frac{s^2}{2a}\,ds,\quad y=\int\limits_0^t\sin\frac{s^2}{2a}\,ds,$$
which are well-known in diffraction theory. The spiral of Cornu touches the horizontal axis at the origin. The asymptotic points are $M_1(\sqrt{\pi a}/2,\sqrt{\pi a}/2)$ and $M_2(-\sqrt{\pi a}/2,-\sqrt{\pi a}/2)$.
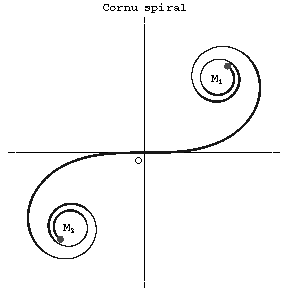
Figure: c026510a
The spiral of Cornu is sometimes called the spiral of Euler after L. Euler, who mentioned it first (1744). Beginning with the works of A. Cornu (1874), the spiral of Cornu is widely used in the calculation of diffraction of light.
References
| [1] | E. Jahnke, F. Emde, F. Lösch, "Tafeln höheren Funktionen" , Teubner (1966) |
| [a1] | J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972) |
Cornu spiral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cornu_spiral&oldid=53388