Difference between revisions of "Etale cohomology"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | e0362801.png | ||
| + | $#A+1 = 38 n = 2 | ||
| + | $#C+1 = 38 : ~/encyclopedia/old_files/data/E036/E.0306280 Etale cohomology | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | The cohomology of sheaves in the étale topology (cf. [[Etale topology|Etale topology]]). It is defined in the standard manner by means of derived functors. Let $ X $ | |
| + | be a scheme and let $ X _ {et} $ | ||
| + | be the étale topology on $ X $. | ||
| + | Then the category of sheaves of Abelian groups on $ X _ {et} $ | ||
| + | is an Abelian category with a sufficient collection of injective objects. The functor $ \Gamma $ | ||
| + | of global sections is left exact and its derived functors $ {\mathcal F} \mapsto H ^ {q} ( X , {\mathcal F} ) $( | ||
| + | where $ {\mathcal F} $ | ||
| + | is a sheaf of Abelian groups on $ X _ {et} $) | ||
| + | are called cohomology functors. Here $ H ^ {0} ( X , {\mathcal F} ) = \Gamma ( {\mathcal F} ) = {\mathcal F} ( X) $. | ||
| + | Similarly, one defines the higher direct images $ R ^ {q} f _ {*} ( {\mathcal F} ) $ | ||
| + | of $ {\mathcal F} $ | ||
| + | relative to a morphism $ f : X \rightarrow Y $; | ||
| + | for them there is an analogue of the [[Leray spectral sequence|Leray spectral sequence]]. If $ {\mathcal F} $ | ||
| + | is a sheaf of non-Abelian groups, one can define the set $ H ^ {1} ( X , {\mathcal F} ) $( | ||
| + | see [[Non-Abelian cohomology|Non-Abelian cohomology]]). | ||
| − | + | The most important results in the theory of étale cohomology are obtained for constructible étale sheaves of Abelian groups. Central among them is the finiteness theorem and the base-change theorem: Let $ f : X \rightarrow Y $ | |
| + | be a proper morphism and let $ {\mathcal F} $ | ||
| + | be a constructible sheaf on $ X $. | ||
| + | Then the sheaves $ R ^ {q} f _ {*} ( {\mathcal F} ) $ | ||
| + | are constructible and the stalk of $ R ^ {q} f _ {*} ( {\mathcal F} ) $ | ||
| + | at a geometric point $ y \rightarrow Y $ | ||
| + | is isomorphic to the cohomology group $ H ^ {q} ( f ^ { - 1 } ( y) , {\mathcal F} ) $ | ||
| + | of the stalk $ f ^ { - 1 } ( y) = X \times _ {Y} y $. | ||
| + | Similar theorems are true for any morphism of finite type, provided that one uses cohomology with compact support. | ||
| − | + | If $ X $ | |
| + | is an algebraic variety over an algebraically closed field, then for any constructible sheaf $ {\mathcal F} $ | ||
| + | on $ X $ | ||
| + | the cohomology groups with compact support $ H _ {C} ^ {q} ( X , {\mathcal F} ) $ | ||
| + | are finite and vanish for $ q > 2 \mathop{\rm dim} X $. | ||
| + | If, in addition, $ X $ | ||
| + | is an affine variety, then $ H ^ {q} ( X , {\mathcal F} ) = 0 $ | ||
| + | for $ q > \mathop{\rm dim} X $. | ||
| − | Etale cohomology of constructible sheaves is used to set up [[L-adic-cohomology| | + | For varieties over the field of complex numbers the étale cohomology of constructible sheaves is the same as the classical cohomology with values in these sheaves. The specialization theorem for a smooth morphism holds: Suppose that $ f : X \rightarrow Y $ |
| + | is a smooth proper morphism of schemes and that the integer $ n $ | ||
| + | is invertible on $ Y $. | ||
| + | Then the sheaves $ R ^ {q} f _ {*} ( \mathbf Z / n \mathbf Z) $ | ||
| + | are locally constant on $ Y $. | ||
| + | |||
| + | For étale cohomology there is an analogue of Poincaré duality (see [[Duality|Duality]] in algebraic geometry) and the [[Künneth formula|Künneth formula]]. Every algebraic cycle of codimension $ i $ | ||
| + | gives a cohomology class in dimension $ 2 i $, | ||
| + | which makes it possible to construct a theory of Chern classes (cf. [[Chern class|Chern class]]). | ||
| + | |||
| + | Etale cohomology of constructible sheaves is used to set up [[L-adic-cohomology| $ l $- | ||
| + | adic cohomology]] and to prove the Weil conjecture on the [[Zeta-function|zeta-function]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Grothendieck, "The cohomology theory of abstract algebraic varieties" , ''Proc. Internat. Math. Congress Edinburgh, 1958'' , Cambridge Univ. Press (1960) pp. 103–118 {{MR|0130879}} {{ZBL|0119.36902}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.S. Milne, "Etale cohomology" , Princeton Univ. Press (1980) {{MR|0559531}} {{ZBL|0433.14012}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> P. Deligne, "Cohomologie étale (SGA 4 1/2)" , ''Lect. notes in math.'' , '''569''' , Springer (1977)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A. Grothendieck, I. Bucur, C. Honzel, L. Illusie, J.-P. Jouanolou, J.-P. Serre, "Cohomologie <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e036/e036280/e03628039.png" />-adique et fonctions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e036/e036280/e03628040.png" />. SGA 5" , ''Lect. notes in math.'' , '''589''' , Springer (1977) {{MR|491704}} {{ZBL|}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> M. Artin (ed.) A. Grothendieck (ed.) J.-L. Verdier (ed.) , ''Théorie des topos et cohomologie étale des schémas (SGA 4)'' , ''Lect. notes in math.'' , '''269; 270; 305''' , Springer (1972–1973)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Grothendieck, "The cohomology theory of abstract algebraic varieties" , ''Proc. Internat. Math. Congress Edinburgh, 1958'' , Cambridge Univ. Press (1960) pp. 103–118 {{MR|0130879}} {{ZBL|0119.36902}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.S. Milne, "Etale cohomology" , Princeton Univ. Press (1980) {{MR|0559531}} {{ZBL|0433.14012}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> P. Deligne, "Cohomologie étale (SGA 4 1/2)" , ''Lect. notes in math.'' , '''569''' , Springer (1977)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A. Grothendieck, I. Bucur, C. Honzel, L. Illusie, J.-P. Jouanolou, J.-P. Serre, "Cohomologie <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e036/e036280/e03628039.png" />-adique et fonctions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e036/e036280/e03628040.png" />. SGA 5" , ''Lect. notes in math.'' , '''589''' , Springer (1977) {{MR|491704}} {{ZBL|}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> M. Artin (ed.) A. Grothendieck (ed.) J.-L. Verdier (ed.) , ''Théorie des topos et cohomologie étale des schémas (SGA 4)'' , ''Lect. notes in math.'' , '''269; 270; 305''' , Springer (1972–1973)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P. Deligue, "La conjecture de Weil I" ''Publ. Math. IHES'' , '''43''' (1974) pp. 273–308</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> P. Deligue, "La conjecture de Weil II" ''Publ. Math. IHES'' , '''52''' (1980) pp. 137–252</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P. Deligue, "La conjecture de Weil I" ''Publ. Math. IHES'' , '''43''' (1974) pp. 273–308</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> P. Deligue, "La conjecture de Weil II" ''Publ. Math. IHES'' , '''52''' (1980) pp. 137–252</TD></TR></table> | ||
Revision as of 19:38, 5 June 2020
The cohomology of sheaves in the étale topology (cf. Etale topology). It is defined in the standard manner by means of derived functors. Let $ X $
be a scheme and let $ X _ {et} $
be the étale topology on $ X $.
Then the category of sheaves of Abelian groups on $ X _ {et} $
is an Abelian category with a sufficient collection of injective objects. The functor $ \Gamma $
of global sections is left exact and its derived functors $ {\mathcal F} \mapsto H ^ {q} ( X , {\mathcal F} ) $(
where $ {\mathcal F} $
is a sheaf of Abelian groups on $ X _ {et} $)
are called cohomology functors. Here $ H ^ {0} ( X , {\mathcal F} ) = \Gamma ( {\mathcal F} ) = {\mathcal F} ( X) $.
Similarly, one defines the higher direct images $ R ^ {q} f _ {*} ( {\mathcal F} ) $
of $ {\mathcal F} $
relative to a morphism $ f : X \rightarrow Y $;
for them there is an analogue of the Leray spectral sequence. If $ {\mathcal F} $
is a sheaf of non-Abelian groups, one can define the set $ H ^ {1} ( X , {\mathcal F} ) $(
see Non-Abelian cohomology).
The most important results in the theory of étale cohomology are obtained for constructible étale sheaves of Abelian groups. Central among them is the finiteness theorem and the base-change theorem: Let $ f : X \rightarrow Y $ be a proper morphism and let $ {\mathcal F} $ be a constructible sheaf on $ X $. Then the sheaves $ R ^ {q} f _ {*} ( {\mathcal F} ) $ are constructible and the stalk of $ R ^ {q} f _ {*} ( {\mathcal F} ) $ at a geometric point $ y \rightarrow Y $ is isomorphic to the cohomology group $ H ^ {q} ( f ^ { - 1 } ( y) , {\mathcal F} ) $ of the stalk $ f ^ { - 1 } ( y) = X \times _ {Y} y $. Similar theorems are true for any morphism of finite type, provided that one uses cohomology with compact support.
If $ X $ is an algebraic variety over an algebraically closed field, then for any constructible sheaf $ {\mathcal F} $ on $ X $ the cohomology groups with compact support $ H _ {C} ^ {q} ( X , {\mathcal F} ) $ are finite and vanish for $ q > 2 \mathop{\rm dim} X $. If, in addition, $ X $ is an affine variety, then $ H ^ {q} ( X , {\mathcal F} ) = 0 $ for $ q > \mathop{\rm dim} X $.
For varieties over the field of complex numbers the étale cohomology of constructible sheaves is the same as the classical cohomology with values in these sheaves. The specialization theorem for a smooth morphism holds: Suppose that $ f : X \rightarrow Y $ is a smooth proper morphism of schemes and that the integer $ n $ is invertible on $ Y $. Then the sheaves $ R ^ {q} f _ {*} ( \mathbf Z / n \mathbf Z) $ are locally constant on $ Y $.
For étale cohomology there is an analogue of Poincaré duality (see Duality in algebraic geometry) and the Künneth formula. Every algebraic cycle of codimension $ i $ gives a cohomology class in dimension $ 2 i $, which makes it possible to construct a theory of Chern classes (cf. Chern class).
Etale cohomology of constructible sheaves is used to set up $ l $- adic cohomology and to prove the Weil conjecture on the zeta-function.
References
| [1] | A. Grothendieck, "The cohomology theory of abstract algebraic varieties" , Proc. Internat. Math. Congress Edinburgh, 1958 , Cambridge Univ. Press (1960) pp. 103–118 MR0130879 Zbl 0119.36902 |
| [2] | J.S. Milne, "Etale cohomology" , Princeton Univ. Press (1980) MR0559531 Zbl 0433.14012 |
| [3] | P. Deligne, "Cohomologie étale (SGA 4 1/2)" , Lect. notes in math. , 569 , Springer (1977) |
| [4] | A. Grothendieck, I. Bucur, C. Honzel, L. Illusie, J.-P. Jouanolou, J.-P. Serre, "Cohomologie 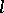 -adique et fonctions -adique et fonctions 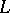 . SGA 5" , Lect. notes in math. , 589 , Springer (1977) MR491704 . SGA 5" , Lect. notes in math. , 589 , Springer (1977) MR491704 |
| [5] | M. Artin (ed.) A. Grothendieck (ed.) J.-L. Verdier (ed.) , Théorie des topos et cohomologie étale des schémas (SGA 4) , Lect. notes in math. , 269; 270; 305 , Springer (1972–1973) |
Comments
References
| [a1] | P. Deligue, "La conjecture de Weil I" Publ. Math. IHES , 43 (1974) pp. 273–308 |
| [a2] | P. Deligue, "La conjecture de Weil II" Publ. Math. IHES , 52 (1980) pp. 137–252 |
Etale cohomology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Etale_cohomology&oldid=46853