Difference between revisions of "Dunford-Pettis property"
Ulf Rehmann (talk | contribs) m (moved Dunford–Pettis property to Dunford-Pettis property: ascii title) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | d1102401.png | ||
| + | $#A+1 = 68 n = 6 | ||
| + | $#C+1 = 68 : ~/encyclopedia/old_files/data/D110/D.1100240 Dunford\ANDPettis property | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | The property | + | The property of a [[Banach space|Banach space]] $ X $ |
| + | that every continuous operator $ T : X \rightarrow Y $ | ||
| + | sending bounded sets of $ X $ | ||
| + | into relatively weakly compact sets of $ Y $( | ||
| + | called weakly compact operators) also transforms weakly compact sets of $ X $ | ||
| + | into norm-compact sets of $ Y $( | ||
| + | such operators are called completely continuous; cf. also [[Completely-continuous operator|Completely-continuous operator]]). In short, it requires that weakly compact operators on $ X $ | ||
| + | are completely continuous. | ||
| − | + | Equivalently, given weakly convergent sequences $ ( x _ {n} ) $ | |
| + | in $ X $ | ||
| + | and $ ( f _ {n} ) $ | ||
| + | in its topological dual $ X ^ {*} $, | ||
| + | the sequence $ ( f _ {n} ( x _ {n} ) ) _ {n} $ | ||
| + | also converges. Contrary to intuition this does not always happen. For example, if $ ( e _ {n} ) $ | ||
| + | denotes the canonical basis of $ l _ {2} $, | ||
| + | then $ ( e _ {n} ) $ | ||
| + | is weakly convergent to zero although $ e _ {n} ( e _ {n} ) = 1 $. | ||
| − | A | + | The property was isolated and defined by A. Grothendieck [[#References|[a7]]] after the following classical result of N. Dunford and B.J. Pettis [[#References|[a5]]]: For any measure $ \mu $ |
| + | and any Banach space $ Y $, | ||
| + | every weakly compact operator $ L _ {1} ( \mu ) $ | ||
| + | into $ Y $ | ||
| + | is completely continuous. | ||
| − | + | This result has its roots in examples of Sirvint, S. Kakutani, Y. Mimura and K. Yosida concerning weakly compact non-compact operators on $ L _ {1} ( 0,1 ) $ | |
| + | which could be proven to have a compact square. The main examples of spaces having the Dunford–Pettis property are the spaces $ C ( K ) $ | ||
| + | of continuous functions on a compact space and the spaces $ L _ {1} ( \mu ) $ | ||
| + | of integrable functions on a measure space, as well as complemented subspaces of these spaces. Other classical function spaces having the Dunford–Pettis property are: the Hardy space $ H ^ \infty $ | ||
| + | and its higher duals (cf. also [[Hardy spaces|Hardy spaces]]); the quotient space $ L _ {1} /H ^ {1} $ | ||
| + | and its higher duals (the space $ H ^ {1} $ | ||
| + | itself does not have the Dunford–Pettis property, nor does its dual BMO or its pre-dual VMO) (cf. also [[BMO-space| $ { \mathop{\rm BMO} } $- | ||
| + | space]]; [[VMO-space| $ { \mathop{\rm VMO} } $- | ||
| + | space]]); the ball algebra, the poly-disc algebra and their duals, and the spaces $ C ^ {k} ( T ^ {n} ) $ | ||
| + | of $ k $- | ||
| + | smooth functions on the $ n $- | ||
| + | dimensional torus. | ||
| − | A [[ | + | A classical survey on the topic is [[#References|[a4]]]. Many of the open problems stated there have been solved by now, mainly by J. Bourgain [[#References|[a2]]], [[#References|[a3]]], who introduced new techniques for working with the Dunford–Pettis property, and by M. Talagrand [[#References|[a8]]], who gave an example of a space $ X $ |
| + | with the Dunford–Pettis property such that $ C ( K,X ) $ | ||
| + | and $ L _ {1} ( \mu,X ^ {*} ) $ | ||
| + | fail the Dunford–Pettis property. | ||
| − | + | The Dunford–Pettis property is not easy to work with, nor is it well understood. In general, it is difficult to prove that a given concrete space has the property; quoting J. Diestel: "I know of no case where the reward (when it comes) is easily attained" . On the question of structure theorems, many open problems remain. One of the most striking is as follows. When does the dual of a space that has the Dunford–Pettis property have the Dunford–Pettis property? It is clear that if $ X ^ {*} $ | |
| + | has the Dunford–Pettis property, then so does $ X $. | ||
| + | From Rosenthal's $ l _ {1} $ | ||
| + | theorem it follows that if $ X $ | ||
| + | has the Dunford–Pettis property and does not contain $ l _ {1} $, | ||
| + | then $ X ^ {*} $ | ||
| + | has the Dunford–Pettis property. Stegall has shown that although the space $ l _ {1} ( l _ {2} ^ {n} ) $ | ||
| + | has the Dunford–Pettis property (since weakly convergent sequences are norm convergent), its dual $ l _ \infty ( l _ {2} ^ {n} ) $ | ||
| + | does not have the Dunford–Pettis property (because it contains complemented copies of $ l _ {2} $). | ||
| − | + | A [[Reflexive space|reflexive space]] does not have the Dunford–Pettis property unless it is finite-dimensional. The Grothendieck spaces $ C ( \Omega ) $, | |
| + | $ L ^ \infty ( \mu ) $, | ||
| + | $ B ( S, \Sigma ) $, | ||
| + | and $ H ^ \infty ( D ) $( | ||
| + | cf. [[Grothendieck space|Grothendieck space]]) also possess the Dunford–Pettis property (see [[#References|[a9]]], [[#References|[a10]]]). | ||
| − | + | A Banach space $ X $ | |
| + | is a Grothendieck space with the Dunford–Pettis property if and only if every weak- $ * $ | ||
| + | convergent sequence in $ X ^ {*} $ | ||
| + | converges weakly and uniformly on weakly compact subsets of $ X $, | ||
| + | if and only if every bounded [[Linear operator|linear operator]] from $ X $ | ||
| + | into $ c _ {0} $ | ||
| + | is weakly compact and maps weakly compact sets into norm-compact sets. | ||
| − | + | An interesting phenomenon about Grothendieck spaces with the Dunford–Pettis property is that in many cases strong convergence of operators on such a space (cf. also [[Strong topology|Strong topology]]) implies [[Uniform convergence|uniform convergence]]. For example, let $ X $ | |
| + | be a Grothendieck space with the Dunford–Pettis property. Then: | ||
| − | + | 1) $ X $ | |
| + | does not have a Schauder decomposition, or equivalently, if a sequence of projections $ \{ P _ {n} \} $ | ||
| + | on $ X $ | ||
| + | converges weakly to the identity operator $ I $, | ||
| + | then $ P _ {n} = I $ | ||
| + | for $ n $ | ||
| + | sufficiently large; | ||
| − | + | 2) if the Cesáro mean $ n ^ {- 1 } \sum _ {k = 0 } ^ {n - 1 } T ^ {k} $ | |
| + | of an operator $ T $ | ||
| + | on $ X $ | ||
| + | converges strongly, then it converges uniformly; | ||
| − | 5) for general ergodic systems on | + | 3) all $ C _ {0} $- |
| + | semi-groups on $ X $ | ||
| + | are norm-continuous (see [[#References|[a9]]], [[#References|[a10]]]); | ||
| + | |||
| + | 4) all strongly continuous cosine operator functions on $ X $ | ||
| + | are norm-continuous [[#References|[a11]]]; | ||
| + | |||
| + | 5) for general ergodic systems on $ X $, | ||
| + | in particular, $ C _ {0} $- | ||
| + | semi-groups and cosine operator functions, strong ergodicity implies uniform ergodicity (see [[#References|[a12]]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Bourgain, "On the Dunford–Pettis property" ''Proc. Amer. Math. Soc.'' , '''81''' (1981) pp. 265–272</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Bourgain, "New Banach space properties of the disc algebra and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110240/d11024070.png" />" ''Acta Math.'' , '''152''' (1984) pp. 1–48</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J. Bourgain, "The Dunford–Pettis property for the ball-algebras, the polydisc algebra, and the Sobolev spaces" ''Studia Math.'' , '''77''' (1984) pp. 245–253</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> J. Diestel, "A survey or results related to the Dunford–Pettis property" , ''Contemp. Math.'' , '''2''' , Amer. Math. Soc. (1980) pp. 15–60</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> N. Dunford, B.J. Pettis, "Linear operations on summable functions" ''Trans. Amer. Math. Soc.'' , '''47''' (1940) pp. 323–392</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> N. Dunford, J.T. Schwartz, "Linear operators" , '''I. General theory''' , Wiley, reprint (1988)</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> A. Grothendieck, "Sur les applications linéaires faiblement compactes d'espaces de type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110240/d11024071.png" />" ''Canad. J. Math.'' , '''5''' (1953) pp. 129–173</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> M. Talagrand, "La propriété de Dunford–Pettis dans <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110240/d11024072.png" /> et <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110240/d11024073.png" />" ''Israel J. Math.'' , '''44''' (1983) pp. 317–321</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> H.P. Lotz, "Tauberian theorems for operators on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110240/d11024074.png" /> and similar spaces" , ''Functional Analysis III. Surveys and Recent Results'' , North-Holland (1984)</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> H.P. Lotz, "Uniform convergence of operators on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110240/d11024075.png" /> and similar spaces" ''Math. Z.'' , '''190''' (1985) pp. 207–220</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> S.-Y. Shaw, "Asymptotic behavior of pseudoresolvents on some Grothendieck spaces" ''Publ. RIMS Kyoto Univ.'' , '''24''' (1988) pp. 277–282</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> S.-Y. Shaw, "Uniform convergence of ergodic limits and approximate solutions" ''Proc. Amer. Math. Soc.'' , '''114''' (1992) pp. 405–411</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Bourgain, "On the Dunford–Pettis property" ''Proc. Amer. Math. Soc.'' , '''81''' (1981) pp. 265–272</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Bourgain, "New Banach space properties of the disc algebra and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110240/d11024070.png" />" ''Acta Math.'' , '''152''' (1984) pp. 1–48</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J. Bourgain, "The Dunford–Pettis property for the ball-algebras, the polydisc algebra, and the Sobolev spaces" ''Studia Math.'' , '''77''' (1984) pp. 245–253</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> J. Diestel, "A survey or results related to the Dunford–Pettis property" , ''Contemp. Math.'' , '''2''' , Amer. Math. Soc. (1980) pp. 15–60</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> N. Dunford, B.J. Pettis, "Linear operations on summable functions" ''Trans. Amer. Math. Soc.'' , '''47''' (1940) pp. 323–392</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> N. Dunford, J.T. Schwartz, "Linear operators" , '''I. General theory''' , Wiley, reprint (1988)</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> A. Grothendieck, "Sur les applications linéaires faiblement compactes d'espaces de type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110240/d11024071.png" />" ''Canad. J. Math.'' , '''5''' (1953) pp. 129–173</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> M. Talagrand, "La propriété de Dunford–Pettis dans <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110240/d11024072.png" /> et <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110240/d11024073.png" />" ''Israel J. Math.'' , '''44''' (1983) pp. 317–321</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> H.P. Lotz, "Tauberian theorems for operators on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110240/d11024074.png" /> and similar spaces" , ''Functional Analysis III. Surveys and Recent Results'' , North-Holland (1984)</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> H.P. Lotz, "Uniform convergence of operators on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110240/d11024075.png" /> and similar spaces" ''Math. Z.'' , '''190''' (1985) pp. 207–220</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> S.-Y. Shaw, "Asymptotic behavior of pseudoresolvents on some Grothendieck spaces" ''Publ. RIMS Kyoto Univ.'' , '''24''' (1988) pp. 277–282</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> S.-Y. Shaw, "Uniform convergence of ergodic limits and approximate solutions" ''Proc. Amer. Math. Soc.'' , '''114''' (1992) pp. 405–411</TD></TR></table> | ||
Revision as of 19:36, 5 June 2020
The property of a Banach space $ X $
that every continuous operator $ T : X \rightarrow Y $
sending bounded sets of $ X $
into relatively weakly compact sets of $ Y $(
called weakly compact operators) also transforms weakly compact sets of $ X $
into norm-compact sets of $ Y $(
such operators are called completely continuous; cf. also Completely-continuous operator). In short, it requires that weakly compact operators on $ X $
are completely continuous.
Equivalently, given weakly convergent sequences $ ( x _ {n} ) $ in $ X $ and $ ( f _ {n} ) $ in its topological dual $ X ^ {*} $, the sequence $ ( f _ {n} ( x _ {n} ) ) _ {n} $ also converges. Contrary to intuition this does not always happen. For example, if $ ( e _ {n} ) $ denotes the canonical basis of $ l _ {2} $, then $ ( e _ {n} ) $ is weakly convergent to zero although $ e _ {n} ( e _ {n} ) = 1 $.
The property was isolated and defined by A. Grothendieck [a7] after the following classical result of N. Dunford and B.J. Pettis [a5]: For any measure $ \mu $ and any Banach space $ Y $, every weakly compact operator $ L _ {1} ( \mu ) $ into $ Y $ is completely continuous.
This result has its roots in examples of Sirvint, S. Kakutani, Y. Mimura and K. Yosida concerning weakly compact non-compact operators on $ L _ {1} ( 0,1 ) $ which could be proven to have a compact square. The main examples of spaces having the Dunford–Pettis property are the spaces $ C ( K ) $ of continuous functions on a compact space and the spaces $ L _ {1} ( \mu ) $ of integrable functions on a measure space, as well as complemented subspaces of these spaces. Other classical function spaces having the Dunford–Pettis property are: the Hardy space $ H ^ \infty $ and its higher duals (cf. also Hardy spaces); the quotient space $ L _ {1} /H ^ {1} $ and its higher duals (the space $ H ^ {1} $ itself does not have the Dunford–Pettis property, nor does its dual BMO or its pre-dual VMO) (cf. also $ { \mathop{\rm BMO} } $- space; $ { \mathop{\rm VMO} } $- space); the ball algebra, the poly-disc algebra and their duals, and the spaces $ C ^ {k} ( T ^ {n} ) $ of $ k $- smooth functions on the $ n $- dimensional torus.
A classical survey on the topic is [a4]. Many of the open problems stated there have been solved by now, mainly by J. Bourgain [a2], [a3], who introduced new techniques for working with the Dunford–Pettis property, and by M. Talagrand [a8], who gave an example of a space $ X $ with the Dunford–Pettis property such that $ C ( K,X ) $ and $ L _ {1} ( \mu,X ^ {*} ) $ fail the Dunford–Pettis property.
The Dunford–Pettis property is not easy to work with, nor is it well understood. In general, it is difficult to prove that a given concrete space has the property; quoting J. Diestel: "I know of no case where the reward (when it comes) is easily attained" . On the question of structure theorems, many open problems remain. One of the most striking is as follows. When does the dual of a space that has the Dunford–Pettis property have the Dunford–Pettis property? It is clear that if $ X ^ {*} $ has the Dunford–Pettis property, then so does $ X $. From Rosenthal's $ l _ {1} $ theorem it follows that if $ X $ has the Dunford–Pettis property and does not contain $ l _ {1} $, then $ X ^ {*} $ has the Dunford–Pettis property. Stegall has shown that although the space $ l _ {1} ( l _ {2} ^ {n} ) $ has the Dunford–Pettis property (since weakly convergent sequences are norm convergent), its dual $ l _ \infty ( l _ {2} ^ {n} ) $ does not have the Dunford–Pettis property (because it contains complemented copies of $ l _ {2} $).
A reflexive space does not have the Dunford–Pettis property unless it is finite-dimensional. The Grothendieck spaces $ C ( \Omega ) $, $ L ^ \infty ( \mu ) $, $ B ( S, \Sigma ) $, and $ H ^ \infty ( D ) $( cf. Grothendieck space) also possess the Dunford–Pettis property (see [a9], [a10]).
A Banach space $ X $ is a Grothendieck space with the Dunford–Pettis property if and only if every weak- $ * $ convergent sequence in $ X ^ {*} $ converges weakly and uniformly on weakly compact subsets of $ X $, if and only if every bounded linear operator from $ X $ into $ c _ {0} $ is weakly compact and maps weakly compact sets into norm-compact sets.
An interesting phenomenon about Grothendieck spaces with the Dunford–Pettis property is that in many cases strong convergence of operators on such a space (cf. also Strong topology) implies uniform convergence. For example, let $ X $ be a Grothendieck space with the Dunford–Pettis property. Then:
1) $ X $ does not have a Schauder decomposition, or equivalently, if a sequence of projections $ \{ P _ {n} \} $ on $ X $ converges weakly to the identity operator $ I $, then $ P _ {n} = I $ for $ n $ sufficiently large;
2) if the Cesáro mean $ n ^ {- 1 } \sum _ {k = 0 } ^ {n - 1 } T ^ {k} $ of an operator $ T $ on $ X $ converges strongly, then it converges uniformly;
3) all $ C _ {0} $- semi-groups on $ X $ are norm-continuous (see [a9], [a10]);
4) all strongly continuous cosine operator functions on $ X $ are norm-continuous [a11];
5) for general ergodic systems on $ X $, in particular, $ C _ {0} $- semi-groups and cosine operator functions, strong ergodicity implies uniform ergodicity (see [a12]).
References
| [a1] | J. Bourgain, "On the Dunford–Pettis property" Proc. Amer. Math. Soc. , 81 (1981) pp. 265–272 |
| [a2] | J. Bourgain, "New Banach space properties of the disc algebra and 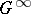 " Acta Math. , 152 (1984) pp. 1–48 " Acta Math. , 152 (1984) pp. 1–48 |
| [a3] | J. Bourgain, "The Dunford–Pettis property for the ball-algebras, the polydisc algebra, and the Sobolev spaces" Studia Math. , 77 (1984) pp. 245–253 |
| [a4] | J. Diestel, "A survey or results related to the Dunford–Pettis property" , Contemp. Math. , 2 , Amer. Math. Soc. (1980) pp. 15–60 |
| [a5] | N. Dunford, B.J. Pettis, "Linear operations on summable functions" Trans. Amer. Math. Soc. , 47 (1940) pp. 323–392 |
| [a6] | N. Dunford, J.T. Schwartz, "Linear operators" , I. General theory , Wiley, reprint (1988) |
| [a7] | A. Grothendieck, "Sur les applications linéaires faiblement compactes d'espaces de type  " Canad. J. Math. , 5 (1953) pp. 129–173 " Canad. J. Math. , 5 (1953) pp. 129–173 |
| [a8] | M. Talagrand, "La propriété de Dunford–Pettis dans 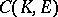 et et 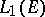 " Israel J. Math. , 44 (1983) pp. 317–321 " Israel J. Math. , 44 (1983) pp. 317–321 |
| [a9] | H.P. Lotz, "Tauberian theorems for operators on 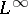 and similar spaces" , Functional Analysis III. Surveys and Recent Results , North-Holland (1984) and similar spaces" , Functional Analysis III. Surveys and Recent Results , North-Holland (1984) |
| [a10] | H.P. Lotz, "Uniform convergence of operators on 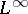 and similar spaces" Math. Z. , 190 (1985) pp. 207–220 and similar spaces" Math. Z. , 190 (1985) pp. 207–220 |
| [a11] | S.-Y. Shaw, "Asymptotic behavior of pseudoresolvents on some Grothendieck spaces" Publ. RIMS Kyoto Univ. , 24 (1988) pp. 277–282 |
| [a12] | S.-Y. Shaw, "Uniform convergence of ergodic limits and approximate solutions" Proc. Amer. Math. Soc. , 114 (1992) pp. 405–411 |
Dunford-Pettis property. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dunford-Pettis_property&oldid=46780