|
|
| Line 1: |
Line 1: |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d1101101.png" /> be a closed <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d1101102.png" />-dimensional [[Manifold|manifold]] and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d1101103.png" /> be a solid torus in the interior of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d1101104.png" />. Remove <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d1101105.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d1101106.png" /> and glue in instead of it another solid torus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d1101107.png" /> by a [[Homeomorphism|homeomorphism]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d1101108.png" />. One says that the resulting new <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d1101109.png" />-dimensional manifold
| + | <!-- |
| | + | d1101101.png |
| | + | $#A+1 = 127 n = 1 |
| | + | $#C+1 = 127 : ~/encyclopedia/old_files/data/D110/D.1100110 Dehn surgery |
| | + | Automatically converted into TeX, above some diagnostics. |
| | + | Please remove this comment and the {{TEX|auto}} line below, |
| | + | if TeX found to be correct. |
| | + | --> |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011010.png" /></td> </tr></table>
| + | {{TEX|auto}} |
| | + | {{TEX|done}} |
| | | | |
| − | is obtained from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011011.png" /> by a Dehn surgery. Note that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011012.png" /> is determined by the following data: 1) a knot <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011013.png" /> (a core circle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011014.png" /> of the solid torus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011015.png" />, cf. also [[Knot theory|Knot theory]]); and 2) a non-trivial simple closed curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011016.png" /> (the image under <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011017.png" /> of a meridian of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011018.png" />). The Dehn surgery is called integer if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011019.png" /> is a longitude of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011020.png" />, i.e., <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011021.png" /> intersects a meridional curve of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011022.png" /> transversally in a single point.
| + | Let $ M $ |
| | + | be a closed $ 3 $- |
| | + | dimensional [[Manifold|manifold]] and let $ N $ |
| | + | be a solid torus in the interior of $ M $. |
| | + | Remove $ { \mathop{\rm Int} } N $ |
| | + | from $ M $ |
| | + | and glue in instead of it another solid torus $ N _ {1} $ |
| | + | by a [[Homeomorphism|homeomorphism]] $ h : {\partial N _ {1} } \rightarrow {\partial N } $. |
| | + | One says that the resulting new $ 3 $- |
| | + | dimensional manifold |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011023.png" />, then among all longitudes of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011024.png" /> there is a preferred one, which bounds a surface in the complement of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011025.png" />. The preferred longitude <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011026.png" /> forms together with a meridian <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011027.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011028.png" /> a coordinate system on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011029.png" />. Therefore, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011030.png" /> has the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011031.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011032.png" /> are coprime integers, and is determined by the rational number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011033.png" />. The Dehn surgery is integer if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011034.png" /> is an integer. This explains the terminology.
| + | $$ |
| | + | M _ {1} = ( M \setminus { \mathop{\rm Int} } N ) \cup _ {h} N _ {1} $$ |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011035.png" /> be two handle-bodies having the same genus (cf. [[Handle theory|Handle theory]]) and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011036.png" /> be a [[Homeomorphism|homeomorphism]]. Denote by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011037.png" /> the closed <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011038.png" />-dimensional manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011039.png" /> obtained by gluing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011040.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011041.png" /> along <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011042.png" />. Choose a simple closed curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011043.png" /> and denote by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011044.png" /> the Dehn twist along <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011045.png" />. To be more precise, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011046.png" /> is a homeomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011047.png" /> obtained by cutting <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011048.png" /> along <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011049.png" />, isotopically rotating one side of the cut by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011050.png" />, and gluing back. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011051.png" />. Since <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011052.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011053.png" /> coincide outside a neighbourhood of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011054.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011055.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011056.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011057.png" /> do actually coincide outside regular neighbourhoods of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011058.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011059.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011060.png" />, respectively. It follows that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011061.png" /> is obtained from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011062.png" /> by a Dehn surgery along <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011063.png" />. One can easily show that the surgery is integer.
| + | is obtained from $ M $ |
| | + | by a Dehn surgery. Note that $ M _ {1} $ |
| | + | is determined by the following data: 1) a knot $ K \subset M $( |
| | + | a core circle $ \{ * \} \times S ^ {1} $ |
| | + | of the solid torus $ N = D ^ {2} \times S ^ {1} $, |
| | + | cf. also [[Knot theory|Knot theory]]); and 2) a non-trivial simple closed curve $ l \subset \partial N $( |
| | + | the image under $ h $ |
| | + | of a meridian of $ N _ {1} $). |
| | + | The Dehn surgery is called integer if $ l $ |
| | + | is a longitude of $ N $, |
| | + | i.e., $ l $ |
| | + | intersects a meridional curve of $ N $ |
| | + | transversally in a single point. |
| | | | |
| − | Define a framed link <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011064.png" /> to be a [[Link|link]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011065.png" /> such that every component <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011066.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011067.png" /> is supplied with an integer number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011068.png" />, called a framing. If one performs Dehn surgeries along all components of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011069.png" />, taking for each component <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011070.png" /> the framing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011071.png" /> as the parameter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011072.png" /> of the surgery, one obtains a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011073.png" />-dimensional manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011074.png" />. Since any orientation-preserving homeomorphism of the boundary of a handle-body is isotopic to a product of Dehn twists [[#References|[a1]]], it follows from the above relation between Dehn twists and integer Dehn surgeries that for every closed orientable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011075.png" />-dimensional manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011076.png" /> there exists a framed link <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011077.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011078.png" />.
| + | If $ M = S ^ {3} $, |
| | + | then among all longitudes of $ N $ |
| | + | there is a preferred one, which bounds a surface in the complement of $ N $. |
| | + | The preferred longitude $ l _ {0} $ |
| | + | forms together with a meridian $ m $ |
| | + | of $ N $ |
| | + | a coordinate system on $ \partial N $. |
| | + | Therefore, $ l $ |
| | + | has the form $ l = m ^ {p} l _ {0} ^ {q} $, |
| | + | where $ p,q $ |
| | + | are coprime integers, and is determined by the rational number $ r = {p / q } $. |
| | + | The Dehn surgery is integer if and only if $ r $ |
| | + | is an integer. This explains the terminology. |
| | | | |
| − | The following question naturally arises: When do two framed links determine homeomorphic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011079.png" />-dimensional manifolds? In 1978 R. Kirby answered this question by showing that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011080.png" /> if and only if one can pass from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011081.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011082.png" /> by a sequence of the following moves and their inverses [[#References|[a2]]]:
| + | Let $ H,H ^ \prime $ |
| | + | be two handle-bodies having the same genus (cf. [[Handle theory|Handle theory]]) and let $ h : {\partial H } \rightarrow {\partial H ^ \prime } $ |
| | + | be a [[Homeomorphism|homeomorphism]]. Denote by $ M $ |
| | + | the closed $ 3 $- |
| | + | dimensional manifold $ H \cap _ {h} H ^ \prime $ |
| | + | obtained by gluing $ H $ |
| | + | and $ H ^ \prime $ |
| | + | along $ h $. |
| | + | Choose a simple closed curve $ s \subset \partial H $ |
| | + | and denote by $ \tau _ {s} $ |
| | + | the Dehn twist along $ s $. |
| | + | To be more precise, $ \tau _ {s} $ |
| | + | is a homeomorphism $ \partial H \rightarrow \partial H $ |
| | + | obtained by cutting $ \partial H $ |
| | + | along $ s $, |
| | + | isotopically rotating one side of the cut by $ 2 \pi $, |
| | + | and gluing back. Let $ M _ {1} = H \cap _ {h \tau _ {s} } H ^ \prime $. |
| | + | Since $ h $ |
| | + | and $ h \tau _ {s} $ |
| | + | coincide outside a neighbourhood of $ s $ |
| | + | in $ \partial H $, |
| | + | $ M $ |
| | + | and $ M _ {1} $ |
| | + | do actually coincide outside regular neighbourhoods of $ s $ |
| | + | in $ M $ |
| | + | and $ M _ {1} $, |
| | + | respectively. It follows that $ M _ {1} $ |
| | + | is obtained from $ M $ |
| | + | by a Dehn surgery along $ s $. |
| | + | One can easily show that the surgery is integer. |
| | | | |
| − | 1) replace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011083.png" /> by the link <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011084.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011085.png" /> is a new unknotted component with framing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011086.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011087.png" /> is contained in a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011088.png" />-dimensional ball <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011089.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011090.png" />;
| + | Define a framed link $ {\mathsf L} $ |
| | + | to be a [[Link|link]] $ L \subset S ^ {3} $ |
| | + | such that every component $ K $ |
| | + | of $ L $ |
| | + | is supplied with an integer number $ \varphi ( K ) $, |
| | + | called a framing. If one performs Dehn surgeries along all components of $ L $, |
| | + | taking for each component $ K \subset L $ |
| | + | the framing $ \varphi ( K ) $ |
| | + | as the parameter $ r $ |
| | + | of the surgery, one obtains a $ 3 $- |
| | + | dimensional manifold $ \chi ( {\mathsf L} ) $. |
| | + | Since any orientation-preserving homeomorphism of the boundary of a handle-body is isotopic to a product of Dehn twists [[#References|[a1]]], it follows from the above relation between Dehn twists and integer Dehn surgeries that for every closed orientable $ 3 $- |
| | + | dimensional manifold $ M $ |
| | + | there exists a framed link $ {\mathsf L} \subset S ^ {3} $ |
| | + | such that $ M = \chi ( {\mathsf L} ) $. |
| | | | |
| − | 2) replace a component <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011091.png" /> by a geometric sum <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011092.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011093.png" />, of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011094.png" /> with another component <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011095.png" /> (see [[#References|[a2]]] for the exact definition of the geometric sum). | + | The following question naturally arises: When do two framed links determine homeomorphic $ 3 $- |
| | + | dimensional manifolds? In 1978 R. Kirby answered this question by showing that $ \chi ( { {\mathsf L} _ {1} } ) = \chi ( { {\mathsf L} _ {2} } ) $ |
| | + | if and only if one can pass from $ { {\mathsf L} _ {1} } $ |
| | + | to $ { {\mathsf L} _ {2} } $ |
| | + | by a sequence of the following moves and their inverses [[#References|[a2]]]: |
| | | | |
| − | This result became broadly known as the Kirby calculus for framed links, thanks to its convenience for presenting <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011096.png" />-dimensional manifolds.
| + | 1) replace $ {\mathsf L} $ |
| | + | by the link $ {\mathsf L} \cup {\mathsf O} $, |
| | + | where $ {\mathsf O} $ |
| | + | is a new unknotted component with framing $ \pm 1 $ |
| | + | such that $ {\mathsf O} $ |
| | + | is contained in a $ 3 $- |
| | + | dimensional ball $ B ^ {3} \subset S ^ {3} $, |
| | + | $ B ^ {3} \cap {\mathsf L} = \emptyset $; |
| | | | |
| − | Recall that a framing of a knot <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011097.png" /> determines a homeomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011098.png" /> of the standard solid torus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d11011099.png" /> onto a regular neighbourhood <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d110110100.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d110110101.png" />. Denote by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d110110102.png" /> the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d110110103.png" />-dimensional manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d110110104.png" /> obtained by attaching a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d110110105.png" />-dimensional handle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d110110106.png" /> of index <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d110110107.png" /> to the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d110110108.png" />-dimensional ball via the homeomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d110110109.png" /> between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d110110110.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d110110111.png" />. It follows from the definition that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d110110112.png" />. Similarly, for any framed link <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d110110113.png" /> the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d110110114.png" />-dimensional manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d110110115.png" /> is the boundary of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d110110116.png" />-dimensional manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d110110117.png" /> obtained by attaching handles of index <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d110110118.png" /> to the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d110110119.png" />-dimensional ball. Move 1) on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d110110120.png" /> corresponds to replacing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d110110121.png" /> by a connected sum of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d110110122.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d110110123.png" />. Move 2) corresponds to a sliding of one handle of index <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d110110124.png" /> over another and does not change <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d110110125.png" />. One can show that any framed link in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d110110126.png" /> can be transformed by moves 1), 2) and their inverses to a link with even framings [[#References|[a3]]]. In the latter case the tangent bundle of the corresponding <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d110/d110110/d110110127.png" />-dimensional manifold is trivial. | + | 2) replace a component $ l _ {i} \subset {\mathsf L} $ |
| | + | by a geometric sum $ l _ {i} + l _ {j} $, |
| | + | $ i \neq j $, |
| | + | of $ l _ {i} $ |
| | + | with another component $ l _ {j} \subset {\mathsf L} $( |
| | + | see [[#References|[a2]]] for the exact definition of the geometric sum). |
| | + | |
| | + | This result became broadly known as the Kirby calculus for framed links, thanks to its convenience for presenting $ 3 $- |
| | + | dimensional manifolds. |
| | + | |
| | + | Recall that a framing of a knot $ K \subset S ^ {3} $ |
| | + | determines a homeomorphism $ h $ |
| | + | of the standard solid torus $ D ^ {2} \times S ^ {1} $ |
| | + | onto a regular neighbourhood $ N $ |
| | + | of $ K $. |
| | + | Denote by $ W ^ {4} ( {\mathsf K} ) $ |
| | + | the $ 4 $- |
| | + | dimensional manifold $ B ^ {4} \cup _ {h} H ^ {4} $ |
| | + | obtained by attaching a $ 4 $- |
| | + | dimensional handle $ H $ |
| | + | of index $ 2 $ |
| | + | to the $ 4 $- |
| | + | dimensional ball via the homeomorphism $ h $ |
| | + | between $ D ^ {2} \times S ^ {1} \subset D ^ {2} \times D ^ {2} = H ^ {4} $ |
| | + | and $ N \subset S ^ {3} = \partial D ^ {4} $. |
| | + | It follows from the definition that $ \partial W ^ {4} ( {\mathsf K} ) = \chi ( {\mathsf K} ) $. |
| | + | Similarly, for any framed link $ {\mathsf L} $ |
| | + | the $ 3 $- |
| | + | dimensional manifold $ \chi ( {\mathsf L} ) $ |
| | + | is the boundary of the $ 4 $- |
| | + | dimensional manifold $ W ^ {4} ( {\mathsf L} ) $ |
| | + | obtained by attaching handles of index $ 2 $ |
| | + | to the $ 4 $- |
| | + | dimensional ball. Move 1) on $ {\mathsf L} $ |
| | + | corresponds to replacing $ W ( {\mathsf L} ) $ |
| | + | by a connected sum of $ W ( {\mathsf L} ) $ |
| | + | with $ \pm CP ^ {2} $. |
| | + | Move 2) corresponds to a sliding of one handle of index $ 2 $ |
| | + | over another and does not change $ W ( {\mathsf L} ) $. |
| | + | One can show that any framed link in $ S ^ {3} $ |
| | + | can be transformed by moves 1), 2) and their inverses to a link with even framings [[#References|[a3]]]. In the latter case the tangent bundle of the corresponding $ 4 $- |
| | + | dimensional manifold is trivial. |
| | | | |
| | See [[#References|[a4]]] for more details. | | See [[#References|[a4]]] for more details. |
Let $ M $
be a closed $ 3 $-
dimensional manifold and let $ N $
be a solid torus in the interior of $ M $.
Remove $ { \mathop{\rm Int} } N $
from $ M $
and glue in instead of it another solid torus $ N _ {1} $
by a homeomorphism $ h : {\partial N _ {1} } \rightarrow {\partial N } $.
One says that the resulting new $ 3 $-
dimensional manifold
$$
M _ {1} = ( M \setminus { \mathop{\rm Int} } N ) \cup _ {h} N _ {1} $$
is obtained from $ M $
by a Dehn surgery. Note that $ M _ {1} $
is determined by the following data: 1) a knot $ K \subset M $(
a core circle $ \{ * \} \times S ^ {1} $
of the solid torus $ N = D ^ {2} \times S ^ {1} $,
cf. also Knot theory); and 2) a non-trivial simple closed curve $ l \subset \partial N $(
the image under $ h $
of a meridian of $ N _ {1} $).
The Dehn surgery is called integer if $ l $
is a longitude of $ N $,
i.e., $ l $
intersects a meridional curve of $ N $
transversally in a single point.
If $ M = S ^ {3} $,
then among all longitudes of $ N $
there is a preferred one, which bounds a surface in the complement of $ N $.
The preferred longitude $ l _ {0} $
forms together with a meridian $ m $
of $ N $
a coordinate system on $ \partial N $.
Therefore, $ l $
has the form $ l = m ^ {p} l _ {0} ^ {q} $,
where $ p,q $
are coprime integers, and is determined by the rational number $ r = {p / q } $.
The Dehn surgery is integer if and only if $ r $
is an integer. This explains the terminology.
Let $ H,H ^ \prime $
be two handle-bodies having the same genus (cf. Handle theory) and let $ h : {\partial H } \rightarrow {\partial H ^ \prime } $
be a homeomorphism. Denote by $ M $
the closed $ 3 $-
dimensional manifold $ H \cap _ {h} H ^ \prime $
obtained by gluing $ H $
and $ H ^ \prime $
along $ h $.
Choose a simple closed curve $ s \subset \partial H $
and denote by $ \tau _ {s} $
the Dehn twist along $ s $.
To be more precise, $ \tau _ {s} $
is a homeomorphism $ \partial H \rightarrow \partial H $
obtained by cutting $ \partial H $
along $ s $,
isotopically rotating one side of the cut by $ 2 \pi $,
and gluing back. Let $ M _ {1} = H \cap _ {h \tau _ {s} } H ^ \prime $.
Since $ h $
and $ h \tau _ {s} $
coincide outside a neighbourhood of $ s $
in $ \partial H $,
$ M $
and $ M _ {1} $
do actually coincide outside regular neighbourhoods of $ s $
in $ M $
and $ M _ {1} $,
respectively. It follows that $ M _ {1} $
is obtained from $ M $
by a Dehn surgery along $ s $.
One can easily show that the surgery is integer.
Define a framed link $ {\mathsf L} $
to be a link $ L \subset S ^ {3} $
such that every component $ K $
of $ L $
is supplied with an integer number $ \varphi ( K ) $,
called a framing. If one performs Dehn surgeries along all components of $ L $,
taking for each component $ K \subset L $
the framing $ \varphi ( K ) $
as the parameter $ r $
of the surgery, one obtains a $ 3 $-
dimensional manifold $ \chi ( {\mathsf L} ) $.
Since any orientation-preserving homeomorphism of the boundary of a handle-body is isotopic to a product of Dehn twists [a1], it follows from the above relation between Dehn twists and integer Dehn surgeries that for every closed orientable $ 3 $-
dimensional manifold $ M $
there exists a framed link $ {\mathsf L} \subset S ^ {3} $
such that $ M = \chi ( {\mathsf L} ) $.
The following question naturally arises: When do two framed links determine homeomorphic $ 3 $-
dimensional manifolds? In 1978 R. Kirby answered this question by showing that $ \chi ( { {\mathsf L} _ {1} } ) = \chi ( { {\mathsf L} _ {2} } ) $
if and only if one can pass from $ { {\mathsf L} _ {1} } $
to $ { {\mathsf L} _ {2} } $
by a sequence of the following moves and their inverses [a2]:
1) replace $ {\mathsf L} $
by the link $ {\mathsf L} \cup {\mathsf O} $,
where $ {\mathsf O} $
is a new unknotted component with framing $ \pm 1 $
such that $ {\mathsf O} $
is contained in a $ 3 $-
dimensional ball $ B ^ {3} \subset S ^ {3} $,
$ B ^ {3} \cap {\mathsf L} = \emptyset $;
2) replace a component $ l _ {i} \subset {\mathsf L} $
by a geometric sum $ l _ {i} + l _ {j} $,
$ i \neq j $,
of $ l _ {i} $
with another component $ l _ {j} \subset {\mathsf L} $(
see [a2] for the exact definition of the geometric sum).
This result became broadly known as the Kirby calculus for framed links, thanks to its convenience for presenting $ 3 $-
dimensional manifolds.
Recall that a framing of a knot $ K \subset S ^ {3} $
determines a homeomorphism $ h $
of the standard solid torus $ D ^ {2} \times S ^ {1} $
onto a regular neighbourhood $ N $
of $ K $.
Denote by $ W ^ {4} ( {\mathsf K} ) $
the $ 4 $-
dimensional manifold $ B ^ {4} \cup _ {h} H ^ {4} $
obtained by attaching a $ 4 $-
dimensional handle $ H $
of index $ 2 $
to the $ 4 $-
dimensional ball via the homeomorphism $ h $
between $ D ^ {2} \times S ^ {1} \subset D ^ {2} \times D ^ {2} = H ^ {4} $
and $ N \subset S ^ {3} = \partial D ^ {4} $.
It follows from the definition that $ \partial W ^ {4} ( {\mathsf K} ) = \chi ( {\mathsf K} ) $.
Similarly, for any framed link $ {\mathsf L} $
the $ 3 $-
dimensional manifold $ \chi ( {\mathsf L} ) $
is the boundary of the $ 4 $-
dimensional manifold $ W ^ {4} ( {\mathsf L} ) $
obtained by attaching handles of index $ 2 $
to the $ 4 $-
dimensional ball. Move 1) on $ {\mathsf L} $
corresponds to replacing $ W ( {\mathsf L} ) $
by a connected sum of $ W ( {\mathsf L} ) $
with $ \pm CP ^ {2} $.
Move 2) corresponds to a sliding of one handle of index $ 2 $
over another and does not change $ W ( {\mathsf L} ) $.
One can show that any framed link in $ S ^ {3} $
can be transformed by moves 1), 2) and their inverses to a link with even framings [a3]. In the latter case the tangent bundle of the corresponding $ 4 $-
dimensional manifold is trivial.
See [a4] for more details.
References
| [a1] | W.B.R. Lickorish, "A representation of orientable combinatorial 3-manifolds" Ann. Math , 76 (1962) pp. 531–540 |
| [a2] | R. Kirby, "A calculus for framed links in 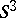 " Invent. Math. , 45 (1978) pp. 35–56 " Invent. Math. , 45 (1978) pp. 35–56 |
| [a3] | S. Kaplan, "Constructing framed 4-manifolds with given almost framed boundaries" Trans. Amer. Math. Soc. , 254 (1979) pp. 237–263 |
| [a4] | A.T. Fomenko, S.V. Matveev, "Algorithmic and computer methods in three dimensional topology" , Kluwer Acad. Publ. (1997) |
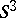 " Invent. Math. , 45 (1978) pp. 35–56
" Invent. Math. , 45 (1978) pp. 35–56