Difference between revisions of "Cubic hypersurface"
m (→Cubic curves.: links) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | A | + | <!-- |
| + | c0272701.png | ||
| + | $#A+1 = 72 n = 1 | ||
| + | $#C+1 = 72 : ~/encyclopedia/old_files/data/C027/C.0207270 Cubic hypersurface | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
| + | A projective algebraic variety defined by a homogeneous equation $ F _ {3} ( x _ {0} \dots x _ {n} ) = 0 $ | ||
| + | of degree three with coefficients in some ground field $ k $. | ||
==Cubic curves.== | ==Cubic curves.== | ||
| − | An irreducible cubic curve is either smooth (in which case its canonical class is 0, its genus 1) or has a unique singular double point (in which case it is rational). Cubic curves are the curves of lowest degree for which there exist moduli (cf. [[Moduli theory|Moduli theory]]). Every smooth cubic curve | + | An irreducible cubic curve is either smooth (in which case its canonical class is 0, its genus 1) or has a unique singular double point (in which case it is rational). Cubic curves are the curves of lowest degree for which there exist moduli (cf. [[Moduli theory|Moduli theory]]). Every smooth cubic curve $ X $ |
| + | over an algebraically closed field $ k $ | ||
| + | of characteristic $ \neq 2 $ | ||
| + | or 3 can be reduced by birational transformations to Weierstrass form, which is, in terms of non-homogeneous coordinates on the $ ( x, y) $- | ||
| + | plane, | ||
| − | + | $$ | |
| + | y ^ {2} = \ | ||
| + | 4x ^ {3} - g _ {2} x - g _ {3} , | ||
| + | $$ | ||
| − | where | + | where $ g _ {2} , g _ {3} \in k $, |
| + | $ g _ {2} ^ {3} - 27g _ {3} ^ {2} \neq 0 $. | ||
| + | Two cubic curves with coefficients $ ( g _ {2} , g _ {3} ) $ | ||
| + | and $ ( g _ {2} ^ \prime , g _ {3} ^ \prime ) $ | ||
| + | in Weierstrass form are isomorphic if and only if | ||
| − | + | $$ | |
| + | |||
| + | \frac{g _ {2} ^ {3} }{g _ {2} ^ {3} - 27g _ {3} ^ {2} } | ||
| + | = \ | ||
| + | |||
| + | \frac{g _ {2} ^ \prime 2 }{g _ {2} ^ \prime 3 - 27g _ {3} ^ \prime 2 } | ||
| + | . | ||
| + | $$ | ||
The function | The function | ||
| − | + | $$ | |
| + | j = \ | ||
| − | + | \frac{1728g _ {2} ^ {3} }{g _ {2} ^ {3} - 27g _ {3} ^ {2} } | |
| − | + | $$ | |
| − | + | takes arbitrary values in $ k $ | |
| + | and depends only on the curve $ X $; | ||
| + | it is called the absolute invariant of $ X $. | ||
| − | + | One can define a binary composition law $ ( x _ {1} , x _ {2} ) \rightarrow x _ {1} \circ x _ {2} $ | |
| + | on the set of points $ X ( k) $ | ||
| + | of a cubic curve: $ x _ {1} \circ x _ {2} $ | ||
| + | is the third point of intersection of $ X $ | ||
| + | with the straight line through $ x _ {1} $ | ||
| + | and $ x _ {2} $. | ||
| + | If one fixes some point $ x _ {0} \in X ( k) $, | ||
| + | the composition | ||
| − | + | $$ | |
| + | ( x _ {1} , x _ {2} ) \rightarrow \ | ||
| + | x _ {0} \circ ( x _ {1} \circ x _ {2} ) | ||
| + | $$ | ||
| − | A rich arithmetic theory has also been developed for cubic curves over algebraically non-closed fields | + | turns $ X ( k) $ |
| + | into an Abelian group with neutral element $ x _ {0} $. | ||
| + | A cubic curve endowed with this structure is a one-dimensional Abelian variety (an elliptic curve). | ||
| + | |||
| + | If $ k = \mathbf C $ | ||
| + | is the field of complex numbers, $ X ( \mathbf C ) $ | ||
| + | is a Riemann surface of genus 1, i.e. a one-dimensional complex torus — a quotient group $ \mathbf C / \Gamma ( X) $, | ||
| + | where $ \Gamma ( X) $ | ||
| + | is a two-dimensional period lattice. The field $ k $ | ||
| + | of rational functions of the curve $ X $ | ||
| + | is then isomorphic to the field of elliptic functions on $ \mathbf C $ | ||
| + | with period lattice $ \Gamma ( X) $. | ||
| + | The coefficients $ g _ {2} , g _ {3} $ | ||
| + | are interpreted as [[modular form]]s of weight 4 and 6, respectively, that are identical, up to a constant factor, with the forms defined by [[Eisenstein series]] of lowest weights. In that case the function $ f $ | ||
| + | is none other than the modular invariant. | ||
| + | |||
| + | A rich arithmetic theory has also been developed for cubic curves over algebraically non-closed fields $ k $( | ||
| + | see [[#References|[2]]]). Significant achievements in that respect are the Mordell–Weil theorem, the theory of complex multiplication and the homology theory of principal homogeneous spaces. The main unsolved problems (as of 1982) are: boundedness of the rank over an algebraic number field; the finiteness conjecture for the group of principal homogeneous locally trivial spaces; the conjecture of Birch and Swinnerton-Dyer on the zeta-function; Weil's uniformization conjecture, etc. (See also [[Elliptic curve|Elliptic curve]].) | ||
==Cubic surfaces.== | ==Cubic surfaces.== | ||
| − | Over an algebraically closed field | + | Over an algebraically closed field $ k $, |
| + | every irreducible cubic surface (that does not degenerate into a cone) is a rational surface. The class of a hyperplane section $ h $ | ||
| + | of a surface $ F $ | ||
| + | is precisely the canonical class $ (- K _ {F} ) $. | ||
| + | Any smooth cubic surface can be obtained from the projective plane $ P ^ {2} $ | ||
| + | by blowing-up (i.e. performing a monoidal transformation) of 6 points, no three of which are collinear, which do not lie on a single conic. The appropriate birational mapping $ \phi : P ^ {2} \rightarrow F $ | ||
| + | is determined by the linear system of cubic curves passing through the 6 points. There are 27 straight lines on $ F $, | ||
| + | each of which is exceptional (see [[Exceptional subvariety|Exceptional subvariety]]); they are the only exceptional curves on $ F $. | ||
| + | The configuration of these 27 lines is rich in symmetries: The automorphism group of the corresponding graph is isomorphic to the Weil group of type $ E _ {6} $. | ||
| + | Cubic surfaces belong to the class of del Pezzo surfaces — projective surfaces with an ample anti-canonical class. | ||
| − | Over an algebraically non-closed field | + | Over an algebraically non-closed field $ k $, |
| + | there are smooth cubic surfaces $ F $ | ||
| + | which are not birationally isomorphic to $ P ^ {2} $ | ||
| + | over $ k $( | ||
| + | i.e. $ F $ | ||
| + | is not rational over $ k $). | ||
| + | Among these surfaces one finds surfaces possessing $ k $- | ||
| + | points, and these are unirational over $ k $. | ||
| + | Such cubic surfaces provide a counterexample for the [[Lüroth problem|Lüroth problem]] on surfaces over non-closed fields. There exist fields $ k $ | ||
| + | over which there are minimal cubic surfaces. Segre's minimality criterion [[#References|[6]]]: $ \mathop{\rm Pic} ( F) \simeq \mathbf Z $. | ||
| + | The group of birational automorphisms of a minimal surface has been determined (in terms of its generators and defining relations) and an arithmetic theory of cubic surfaces has been developed [[#References|[4]]]. In order to describe the set of points $ F ( k) $ | ||
| + | one appeals to non-associative structures, such as quasi-groups and Moufang loops. | ||
==Cubic hypersurfaces of dimension 3.== | ==Cubic hypersurfaces of dimension 3.== | ||
| − | All smooth cubic hypersurfaces of dimension | + | All smooth cubic hypersurfaces of dimension $ \geq 2 $ |
| + | over an algebraically closed field are unirational. As far back as the eighties of the 19th century, the following question was posed: Is a smooth three-dimensional cubic hypersurface rational? A negative answer has been obtained [[#References|[3]]]. This also provides a negative solution to the Lüroth problem for three-dimensional varieties. For every smooth three-dimensional cubic hypersurface $ V $ | ||
| + | there exists a principal polarized five-dimensional Abelian variety — the intermediate Jacobian $ J _ {3} ( V) $. | ||
| + | If $ k = \mathbf C $ | ||
| + | it is defined as as the complex torus | ||
| − | + | $$ | |
| + | H ^ {1,2} ( V, \mathbf C )/H ^ {3} ( V, \mathbf Z ), | ||
| + | $$ | ||
| − | where | + | where $ H ^ {1,2} ( V, \mathbf C ) $ |
| + | is the corresponding Hodge component in the decomposition of the homology space $ H ^ {3} ( V, \mathbf C ) $. | ||
| + | In order to prove that $ V $ | ||
| + | is non-rational, it was shown that $ J _ {3} ( V) $ | ||
| + | is not the Jacobian of any curve of genus 5. The fact that a cubic hypersurface over a field of finite characteristic is non-rational was established in [[#References|[5]]]. | ||
| − | A cubic hypersurface | + | A cubic hypersurface $ V $ |
| + | is uniquely determined by its [[Fano surface|Fano surface]] $ \Phi ( V) $. | ||
| + | For $ \Phi ( V) $ | ||
| + | one has the [[Torelli theorems|Torelli theorems]] (which are also valid for $ V $ | ||
| + | itself). The following problem is unsolved: Given a three-dimensional cubic hypersurface, describe its group of birational automorphisms. | ||
| − | It is not known (1987) whether every smooth cubic hypersurface of dimension | + | It is not known (1987) whether every smooth cubic hypersurface of dimension $ \geq 4 $ |
| + | is rational. Rationality has been proved in this case for certain hypersurfaces of a special type; for example: | ||
| − | + | $$ | |
| + | \sum _ {i = 0 } ^ { {2m } + 1 } | ||
| + | a _ {i} x _ {i} ^ {3} = 0,\ \ | ||
| + | m \geq 2. | ||
| + | $$ | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , Springer (1964) {{MR|0173749}} {{ZBL|0135.12101}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.W.S. Cassels, "Diophantine equations with special reference to elliptic curves" ''J. London Math. Soc.'' , '''41''' (1966) pp. 193–291 {{MR|0199150}} {{ZBL|0138.27002}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> C.H. Clemens, P.A. Griffiths, "The intermediate Jacobian of the cubic threefold" ''Ann. of Math.'' , '''95''' (1972) pp. 281–356 {{MR|0302652}} {{ZBL|0245.14010}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> Yu.I. Manin, "Cubic forms. Algebra, geometry, arithmetic" , North-Holland (1986) (Translated from Russian) {{MR|0833513}} {{ZBL|0582.14010}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> J.P. Murre, "Reduction of the proof of the non-rationality of a non-singular cubic threefold to a result of Mumford" ''Comp. Math.'' , '''27''' (1973) pp. 63–82 {{MR|0352088}} {{MR|0352089}} {{ZBL|0271.14020}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> B. Segre, "The non-singular cubic surfaces" , Clarendon Press (1942) {{MR|0008171}} {{ZBL|0061.36701}} {{ZBL|68.0358.01}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> A.N. Tyurin, "Five lectures on three-dimensional varieties" ''Russian Math. Surveys'' , '''27''' (1972) pp. 1–53 ''Uspekhi Mat. Nauk'' , '''27''' : 5 (1972) pp. 3–50 {{MR|}} {{ZBL|0263.14012}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> A.N. Tyurin, "The geometry of the Fano surface of a nonsingular cubic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027270/c02727073.png" /> and Torelli theorems for Fano surfaces and cubics" ''Math. USSR-Izv.'' , '''5''' : 3 (1971) pp. 517–546 ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''35''' (1971) pp. 498–529 {{MR|}} {{ZBL|0215.08201}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) {{MR|0447223}} {{ZBL|0362.14001}} </TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , Springer (1964) {{MR|0173749}} {{ZBL|0135.12101}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.W.S. Cassels, "Diophantine equations with special reference to elliptic curves" ''J. London Math. Soc.'' , '''41''' (1966) pp. 193–291 {{MR|0199150}} {{ZBL|0138.27002}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> C.H. Clemens, P.A. Griffiths, "The intermediate Jacobian of the cubic threefold" ''Ann. of Math.'' , '''95''' (1972) pp. 281–356 {{MR|0302652}} {{ZBL|0245.14010}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> Yu.I. Manin, "Cubic forms. Algebra, geometry, arithmetic" , North-Holland (1986) (Translated from Russian) {{MR|0833513}} {{ZBL|0582.14010}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> J.P. Murre, "Reduction of the proof of the non-rationality of a non-singular cubic threefold to a result of Mumford" ''Comp. Math.'' , '''27''' (1973) pp. 63–82 {{MR|0352088}} {{MR|0352089}} {{ZBL|0271.14020}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> B. Segre, "The non-singular cubic surfaces" , Clarendon Press (1942) {{MR|0008171}} {{ZBL|0061.36701}} {{ZBL|68.0358.01}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> A.N. Tyurin, "Five lectures on three-dimensional varieties" ''Russian Math. Surveys'' , '''27''' (1972) pp. 1–53 ''Uspekhi Mat. Nauk'' , '''27''' : 5 (1972) pp. 3–50 {{MR|}} {{ZBL|0263.14012}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> A.N. Tyurin, "The geometry of the Fano surface of a nonsingular cubic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027270/c02727073.png" /> and Torelli theorems for Fano surfaces and cubics" ''Math. USSR-Izv.'' , '''5''' : 3 (1971) pp. 517–546 ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''35''' (1971) pp. 498–529 {{MR|}} {{ZBL|0215.08201}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) {{MR|0447223}} {{ZBL|0362.14001}} </TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) {{MR|0507725}} {{ZBL|0408.14001}} </TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) {{MR|0507725}} {{ZBL|0408.14001}} </TD></TR></table> | ||
Revision as of 17:31, 5 June 2020
A projective algebraic variety defined by a homogeneous equation $ F _ {3} ( x _ {0} \dots x _ {n} ) = 0 $
of degree three with coefficients in some ground field $ k $.
Cubic curves.
An irreducible cubic curve is either smooth (in which case its canonical class is 0, its genus 1) or has a unique singular double point (in which case it is rational). Cubic curves are the curves of lowest degree for which there exist moduli (cf. Moduli theory). Every smooth cubic curve $ X $ over an algebraically closed field $ k $ of characteristic $ \neq 2 $ or 3 can be reduced by birational transformations to Weierstrass form, which is, in terms of non-homogeneous coordinates on the $ ( x, y) $- plane,
$$ y ^ {2} = \ 4x ^ {3} - g _ {2} x - g _ {3} , $$
where $ g _ {2} , g _ {3} \in k $, $ g _ {2} ^ {3} - 27g _ {3} ^ {2} \neq 0 $. Two cubic curves with coefficients $ ( g _ {2} , g _ {3} ) $ and $ ( g _ {2} ^ \prime , g _ {3} ^ \prime ) $ in Weierstrass form are isomorphic if and only if
$$ \frac{g _ {2} ^ {3} }{g _ {2} ^ {3} - 27g _ {3} ^ {2} } = \ \frac{g _ {2} ^ \prime 2 }{g _ {2} ^ \prime 3 - 27g _ {3} ^ \prime 2 } . $$
The function
$$ j = \ \frac{1728g _ {2} ^ {3} }{g _ {2} ^ {3} - 27g _ {3} ^ {2} } $$
takes arbitrary values in $ k $ and depends only on the curve $ X $; it is called the absolute invariant of $ X $.
One can define a binary composition law $ ( x _ {1} , x _ {2} ) \rightarrow x _ {1} \circ x _ {2} $ on the set of points $ X ( k) $ of a cubic curve: $ x _ {1} \circ x _ {2} $ is the third point of intersection of $ X $ with the straight line through $ x _ {1} $ and $ x _ {2} $. If one fixes some point $ x _ {0} \in X ( k) $, the composition
$$ ( x _ {1} , x _ {2} ) \rightarrow \ x _ {0} \circ ( x _ {1} \circ x _ {2} ) $$
turns $ X ( k) $ into an Abelian group with neutral element $ x _ {0} $. A cubic curve endowed with this structure is a one-dimensional Abelian variety (an elliptic curve).
If $ k = \mathbf C $ is the field of complex numbers, $ X ( \mathbf C ) $ is a Riemann surface of genus 1, i.e. a one-dimensional complex torus — a quotient group $ \mathbf C / \Gamma ( X) $, where $ \Gamma ( X) $ is a two-dimensional period lattice. The field $ k $ of rational functions of the curve $ X $ is then isomorphic to the field of elliptic functions on $ \mathbf C $ with period lattice $ \Gamma ( X) $. The coefficients $ g _ {2} , g _ {3} $ are interpreted as modular forms of weight 4 and 6, respectively, that are identical, up to a constant factor, with the forms defined by Eisenstein series of lowest weights. In that case the function $ f $ is none other than the modular invariant.
A rich arithmetic theory has also been developed for cubic curves over algebraically non-closed fields $ k $( see [2]). Significant achievements in that respect are the Mordell–Weil theorem, the theory of complex multiplication and the homology theory of principal homogeneous spaces. The main unsolved problems (as of 1982) are: boundedness of the rank over an algebraic number field; the finiteness conjecture for the group of principal homogeneous locally trivial spaces; the conjecture of Birch and Swinnerton-Dyer on the zeta-function; Weil's uniformization conjecture, etc. (See also Elliptic curve.)
Cubic surfaces.
Over an algebraically closed field $ k $, every irreducible cubic surface (that does not degenerate into a cone) is a rational surface. The class of a hyperplane section $ h $ of a surface $ F $ is precisely the canonical class $ (- K _ {F} ) $. Any smooth cubic surface can be obtained from the projective plane $ P ^ {2} $ by blowing-up (i.e. performing a monoidal transformation) of 6 points, no three of which are collinear, which do not lie on a single conic. The appropriate birational mapping $ \phi : P ^ {2} \rightarrow F $ is determined by the linear system of cubic curves passing through the 6 points. There are 27 straight lines on $ F $, each of which is exceptional (see Exceptional subvariety); they are the only exceptional curves on $ F $. The configuration of these 27 lines is rich in symmetries: The automorphism group of the corresponding graph is isomorphic to the Weil group of type $ E _ {6} $. Cubic surfaces belong to the class of del Pezzo surfaces — projective surfaces with an ample anti-canonical class.
Over an algebraically non-closed field $ k $, there are smooth cubic surfaces $ F $ which are not birationally isomorphic to $ P ^ {2} $ over $ k $( i.e. $ F $ is not rational over $ k $). Among these surfaces one finds surfaces possessing $ k $- points, and these are unirational over $ k $. Such cubic surfaces provide a counterexample for the Lüroth problem on surfaces over non-closed fields. There exist fields $ k $ over which there are minimal cubic surfaces. Segre's minimality criterion [6]: $ \mathop{\rm Pic} ( F) \simeq \mathbf Z $. The group of birational automorphisms of a minimal surface has been determined (in terms of its generators and defining relations) and an arithmetic theory of cubic surfaces has been developed [4]. In order to describe the set of points $ F ( k) $ one appeals to non-associative structures, such as quasi-groups and Moufang loops.
Cubic hypersurfaces of dimension 3.
All smooth cubic hypersurfaces of dimension $ \geq 2 $ over an algebraically closed field are unirational. As far back as the eighties of the 19th century, the following question was posed: Is a smooth three-dimensional cubic hypersurface rational? A negative answer has been obtained [3]. This also provides a negative solution to the Lüroth problem for three-dimensional varieties. For every smooth three-dimensional cubic hypersurface $ V $ there exists a principal polarized five-dimensional Abelian variety — the intermediate Jacobian $ J _ {3} ( V) $. If $ k = \mathbf C $ it is defined as as the complex torus
$$ H ^ {1,2} ( V, \mathbf C )/H ^ {3} ( V, \mathbf Z ), $$
where $ H ^ {1,2} ( V, \mathbf C ) $ is the corresponding Hodge component in the decomposition of the homology space $ H ^ {3} ( V, \mathbf C ) $. In order to prove that $ V $ is non-rational, it was shown that $ J _ {3} ( V) $ is not the Jacobian of any curve of genus 5. The fact that a cubic hypersurface over a field of finite characteristic is non-rational was established in [5].
A cubic hypersurface $ V $ is uniquely determined by its Fano surface $ \Phi ( V) $. For $ \Phi ( V) $ one has the Torelli theorems (which are also valid for $ V $ itself). The following problem is unsolved: Given a three-dimensional cubic hypersurface, describe its group of birational automorphisms.
It is not known (1987) whether every smooth cubic hypersurface of dimension $ \geq 4 $ is rational. Rationality has been proved in this case for certain hypersurfaces of a special type; for example:
$$ \sum _ {i = 0 } ^ { {2m } + 1 } a _ {i} x _ {i} ^ {3} = 0,\ \ m \geq 2. $$
References
| [1] | A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , Springer (1964) MR0173749 Zbl 0135.12101 |
| [2] | J.W.S. Cassels, "Diophantine equations with special reference to elliptic curves" J. London Math. Soc. , 41 (1966) pp. 193–291 MR0199150 Zbl 0138.27002 |
| [3] | C.H. Clemens, P.A. Griffiths, "The intermediate Jacobian of the cubic threefold" Ann. of Math. , 95 (1972) pp. 281–356 MR0302652 Zbl 0245.14010 |
| [4] | Yu.I. Manin, "Cubic forms. Algebra, geometry, arithmetic" , North-Holland (1986) (Translated from Russian) MR0833513 Zbl 0582.14010 |
| [5] | J.P. Murre, "Reduction of the proof of the non-rationality of a non-singular cubic threefold to a result of Mumford" Comp. Math. , 27 (1973) pp. 63–82 MR0352088 MR0352089 Zbl 0271.14020 |
| [6] | B. Segre, "The non-singular cubic surfaces" , Clarendon Press (1942) MR0008171 Zbl 0061.36701 Zbl 68.0358.01 |
| [7] | A.N. Tyurin, "Five lectures on three-dimensional varieties" Russian Math. Surveys , 27 (1972) pp. 1–53 Uspekhi Mat. Nauk , 27 : 5 (1972) pp. 3–50 Zbl 0263.14012 |
| [8] | A.N. Tyurin, "The geometry of the Fano surface of a nonsingular cubic 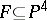 and Torelli theorems for Fano surfaces and cubics" Math. USSR-Izv. , 5 : 3 (1971) pp. 517–546 Izv. Akad. Nauk SSSR Ser. Mat. , 35 (1971) pp. 498–529 Zbl 0215.08201 and Torelli theorems for Fano surfaces and cubics" Math. USSR-Izv. , 5 : 3 (1971) pp. 517–546 Izv. Akad. Nauk SSSR Ser. Mat. , 35 (1971) pp. 498–529 Zbl 0215.08201 |
| [9] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) MR0447223 Zbl 0362.14001 |
Comments
References
| [a1] | P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) MR0507725 Zbl 0408.14001 |
Cubic hypersurface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cubic_hypersurface&oldid=46563