Difference between revisions of "Buekenhout-Metz unital"
From Encyclopedia of Mathematics
Ulf Rehmann (talk | contribs) m (moved Buekenhout–Metz unital to Buekenhout-Metz unital: ascii title) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | b1110101.png | ||
| + | $#A+1 = 48 n = 2 | ||
| + | $#C+1 = 48 : ~/encyclopedia/old_files/data/B111/B.1101010 Buekenhout\ANDMetz unital | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A type of [[Unital|unital]] constructed from $ { \mathop{\rm PG} } ( 4,q ) $ | |
| + | via the construction of a translation plane (cf. [[Translation surface|Translation surface]]). Let $ \Pi $ | ||
| + | be a hyperplane of $ { \mathop{\rm PG} } ( 4,q ) $ | ||
| + | and let $ S $ | ||
| + | be a spread, that is a set of lines, necessarily $ q ^ {2} + 1 $ | ||
| + | in number, partitioning $ \Pi $. | ||
| + | Define an incidence structure $ {\mathcal I} = ( {\mathcal P}, {\mathcal B} ) $( | ||
| + | cf. [[Incidence system|Incidence system]]), where the elements of $ {\mathcal P} $ | ||
| + | are the $ q ^ {4} $ | ||
| + | points of $ { \mathop{\rm PG} } ( 4,q ) \backslash \Pi $ | ||
| + | and the $ q ^ {2} + 1 $ | ||
| + | lines of $ S $. | ||
| + | The elements of $ {\mathcal B} $ | ||
| + | are the $ q ^ {4} + q ^ {2} $ | ||
| + | planes of $ { \mathop{\rm PG} } ( 4,q ) $ | ||
| + | meeting $ \Pi $ | ||
| + | in precisely a line of $ S $ | ||
| + | and the single element $ S $. | ||
| + | Incidence is inclusion. Then $ {\mathcal I} $ | ||
| + | is a [[Projective plane|projective plane]], which is Desarguesian (cf. [[Desargues geometry|Desargues geometry]]) if $ S $ | ||
| + | is regular, that is, if it has the property that three tranversals of three lines of $ S $ | ||
| + | are transversals of $ q + 1 $ | ||
| + | lines of $ S $. | ||
| − | is the eponymous unital in | + | Now, let $ O $ |
| + | be an [[Ovoid(2)|ovoid]], that is, a set of $ q ^ {2} + 1 $ | ||
| + | points, no three collinear, in a hyperplane $ \Pi ^ \prime $ | ||
| + | other than $ \Pi $ | ||
| + | such that $ O \cap \Pi $ | ||
| + | is the single point $ P $, | ||
| + | where $ P $ | ||
| + | is not on the line $ \Pi \cap \Pi ^ \prime $. | ||
| + | Let $ {\mathcal l} $ | ||
| + | be the line of $ S $ | ||
| + | through $ P $ | ||
| + | and let $ Q $ | ||
| + | be a point of $ {\mathcal l} $ | ||
| + | other than $ P $. | ||
| + | Then, with $ QO $ | ||
| + | the cone with vertex $ Q $ | ||
| + | and base $ O $, | ||
| + | |||
| + | $$ | ||
| + | {\mathcal U} = ( QO \backslash {\mathcal l} ) \cup \{ {\mathcal l} \} | ||
| + | $$ | ||
| + | |||
| + | is the eponymous unital in $ {\mathcal I} $. | ||
| + | If $ {\mathcal I} $ | ||
| + | is Desarguesian, both the Tits ovoid when $ q = 2 ^ {2e + 1 } $ | ||
| + | with $ e \geq 1 $ | ||
| + | and a suitably chosen elliptic quadric for arbitrary $ q $ | ||
| + | with $ q > 2 $ | ||
| + | give a unital, also called in this case a Hermitian arc, that is not a Hermitian curve [[#References|[a1]]], [[#References|[a3]]]. An explicit equation of degree $ 2q $ | ||
| + | can be given [[#References|[a2]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> F. Buekenhout, "Existence of unitals in finite translation planes of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b111/b111010/b11101049.png" /> with a kernel of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b111/b111010/b11101050.png" />" ''Geom. Dedicata'' , '''5''' (1976) pp. 189–194</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.W.P. Hirschfeld, "Finite projective spaces of three dimensions" , Oxford Univ. Press (1985)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> R. Metz, "On a class of unitals" ''Geom. Dedicata'' , '''8''' (1979) pp. 125–126</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> F. Buekenhout, "Existence of unitals in finite translation planes of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b111/b111010/b11101049.png" /> with a kernel of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b111/b111010/b11101050.png" />" ''Geom. Dedicata'' , '''5''' (1976) pp. 189–194</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.W.P. Hirschfeld, "Finite projective spaces of three dimensions" , Oxford Univ. Press (1985)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> R. Metz, "On a class of unitals" ''Geom. Dedicata'' , '''8''' (1979) pp. 125–126</TD></TR></table> | ||
Revision as of 06:29, 30 May 2020
A type of unital constructed from $ { \mathop{\rm PG} } ( 4,q ) $
via the construction of a translation plane (cf. Translation surface). Let $ \Pi $
be a hyperplane of $ { \mathop{\rm PG} } ( 4,q ) $
and let $ S $
be a spread, that is a set of lines, necessarily $ q ^ {2} + 1 $
in number, partitioning $ \Pi $.
Define an incidence structure $ {\mathcal I} = ( {\mathcal P}, {\mathcal B} ) $(
cf. Incidence system), where the elements of $ {\mathcal P} $
are the $ q ^ {4} $
points of $ { \mathop{\rm PG} } ( 4,q ) \backslash \Pi $
and the $ q ^ {2} + 1 $
lines of $ S $.
The elements of $ {\mathcal B} $
are the $ q ^ {4} + q ^ {2} $
planes of $ { \mathop{\rm PG} } ( 4,q ) $
meeting $ \Pi $
in precisely a line of $ S $
and the single element $ S $.
Incidence is inclusion. Then $ {\mathcal I} $
is a projective plane, which is Desarguesian (cf. Desargues geometry) if $ S $
is regular, that is, if it has the property that three tranversals of three lines of $ S $
are transversals of $ q + 1 $
lines of $ S $.
Now, let $ O $ be an ovoid, that is, a set of $ q ^ {2} + 1 $ points, no three collinear, in a hyperplane $ \Pi ^ \prime $ other than $ \Pi $ such that $ O \cap \Pi $ is the single point $ P $, where $ P $ is not on the line $ \Pi \cap \Pi ^ \prime $. Let $ {\mathcal l} $ be the line of $ S $ through $ P $ and let $ Q $ be a point of $ {\mathcal l} $ other than $ P $. Then, with $ QO $ the cone with vertex $ Q $ and base $ O $,
$$ {\mathcal U} = ( QO \backslash {\mathcal l} ) \cup \{ {\mathcal l} \} $$
is the eponymous unital in $ {\mathcal I} $. If $ {\mathcal I} $ is Desarguesian, both the Tits ovoid when $ q = 2 ^ {2e + 1 } $ with $ e \geq 1 $ and a suitably chosen elliptic quadric for arbitrary $ q $ with $ q > 2 $ give a unital, also called in this case a Hermitian arc, that is not a Hermitian curve [a1], [a3]. An explicit equation of degree $ 2q $ can be given [a2].
References
| [a1] | F. Buekenhout, "Existence of unitals in finite translation planes 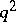of order  with a kernel of order 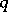 " Geom. Dedicata , 5 (1976) pp. 189–194 |
| [a2] | J.W.P. Hirschfeld, "Finite projective spaces of three dimensions" , Oxford Univ. Press (1985) |
| [a3] | R. Metz, "On a class of unitals" Geom. Dedicata , 8 (1979) pp. 125–126 |
How to Cite This Entry:
Buekenhout-Metz unital. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Buekenhout-Metz_unital&oldid=46172
Buekenhout-Metz unital. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Buekenhout-Metz_unital&oldid=46172
This article was adapted from an original article by J.W.P. Hirschfeld (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article