Difference between revisions of "Brauer homomorphism"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | b1108601.png | ||
| + | $#A+1 = 63 n = 1 | ||
| + | $#C+1 = 63 : ~/encyclopedia/old_files/data/B110/B.1100860 Brauer homomorphism | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | The Brauer homomorphism was first used by R. Brauer [[#References|[a1]]], [[#References|[a2]]], and developed further by H. Nagao [[#References|[a4]]] to establish a connection between the $ p $- | |
| + | blocks of a [[Finite group|finite group]] $ G $ | ||
| + | and of the $ p $- | ||
| + | local subgroups (cf. [[Block|Block]]). Subsequently, it has been used in a variety of other contexts within modular representation theory (cf. also [[Finite group, representation of a|Finite group, representation of a]]). | ||
| − | + | Let $ k $ | |
| + | be a [[Field|field]] of characteristic $ p $, | ||
| + | and let $ G $ | ||
| + | act by conjugation on the [[Group algebra|group algebra]] $ kG $ | ||
| + | with fixed points $ ( kG ) ^ {G} = Z ( kG ) $. | ||
| + | The primitive idempotents $ e _ {0} \dots e _ {s} $ | ||
| + | in $ Z ( kG ) $ | ||
| + | correspond to the blocks $ B _ {0} \dots B _ {s} $ | ||
| + | of $ kG $, | ||
| + | so that $ B _ {i} = e _ {i} kG $ | ||
| + | and $ kG = B _ {0} \oplus \dots \oplus B _ {s} $ | ||
| + | as a direct sum of indecomposable two-sided ideals. | ||
| − | + | If $ H \leq K $ | |
| + | are subgroups of $ G $ | ||
| + | and $ M $ | ||
| + | is a $ kG $- | ||
| + | module, there is a relative trace mapping $ { { \mathop{\rm Tr} } _ {H,K } } : {M ^ {H} } \rightarrow {M ^ {K} } $, | ||
| + | given by $ m \mapsto \sum _ {i} g _ {i} m $, | ||
| + | where $ g _ {i} $ | ||
| + | runs through a set of coset representatives of $ H $ | ||
| + | in $ K $. | ||
| + | One writes $ M _ {H} ^ {K} $ | ||
| + | for the image of $ { \mathop{\rm Tr} } _ {H,K } $. | ||
| + | Applying this to the conjugation action of $ G $ | ||
| + | on $ kG $, | ||
| + | one says that $ D $ | ||
| + | is a defect group for the [[Block|block]] $ B _ {i} $( | ||
| + | cf. also [[Defect group of a block|Defect group of a block]]) if $ e _ {i} $ | ||
| + | lies in $ ( kG ) _ {D} ^ {G} $ | ||
| + | but not in $ ( kG ) _ {D ^ \prime } ^ {D} $ | ||
| + | for any proper subgroup $ D ^ \prime < D $. | ||
| + | The defect groups of a block form a single conjugacy class of $ p $- | ||
| + | subgroups of $ G $. | ||
| − | + | If $ D $ | |
| + | is any $ p $- | ||
| + | subgroup of $ G $, | ||
| + | still acting on $ G $ | ||
| + | by conjugation, then there is a decomposition | ||
| − | + | $$ | |
| + | ( kG ) ^ {D} = kC _ {G} ( D ) \oplus \sum _ {D ^ \prime < D } ( kG ) _ {D ^ \prime } ^ {D} | ||
| + | $$ | ||
| − | is the | + | as a direct sum of a subring and a two-sided ideal. This is because the left-hand side has as a basis the orbit sums. The orbits of length one span $ kC _ {G} ( D ) $, |
| + | and the sums of orbits of length greater than one are transfers from proper subgroups of $ D $. | ||
| + | The Brauer homomorphism | ||
| − | + | $$ | |
| + | { { \mathop{\rm Br} } _ {D} } : {( kG ) ^ {D} } \rightarrow {kC _ {G} ( D ) } | ||
| + | $$ | ||
| + | |||
| + | is the projection onto the first factor in the above decomposition. Restricting to $ Z ( kG ) = ( kG ) ^ {G} \subseteq ( kG ) ^ {D} $, | ||
| + | one obtains the homomorphism | ||
| + | |||
| + | $$ | ||
| + | { { \mathop{\rm Br} } _ {D} } : {Z ( kG ) } \rightarrow {Z ( kC _ {G} ( D ) ) } | ||
| + | $$ | ||
originally considered by Brauer. | originally considered by Brauer. | ||
| − | Brauer's first main theorem states that the Brauer homomorphism | + | Brauer's first main theorem states that the Brauer homomorphism $ { \mathop{\rm Br} } _ {D} $ |
| + | establishes a one-to-one correspondence between the blocks of $ G $ | ||
| + | with defect group $ D $ | ||
| + | and the blocks of $ N _ {G} ( D ) $ | ||
| + | with defect group $ D $. | ||
| + | To make sense of this, first observe that every idempotent in $ Z ( kN _ {G} ( D ) ) $ | ||
| + | lies in $ Z ( kC _ {G} ( D ) ) $( | ||
| + | because the other summand $ \sum _ {D ^ \prime < D } ( kN _ {G} ( D ) ) _ {D ^ \prime } ^ {D} $ | ||
| + | is contained in the [[Jacobson radical|Jacobson radical]] $ J ( kN _ {G} ( D ) ) $). | ||
| + | A block idempotent $ e _ {i} \in Z ( kG ) $ | ||
| + | has defect group $ D $ | ||
| + | if and only if $ e _ {i} \in ( kG ) _ {D} ^ {G} $ | ||
| + | and $ { \mathop{\rm Br} } _ {D} ( e _ {i} ) \neq 0 $. | ||
| + | In the commutative diagram | ||
| + | |||
| + | $$ | ||
| + | |||
| + | \begin{array}{ccc} | ||
| + | ( kG ) ^ {D} & \mathop \rightarrow \limits ^ { {{ \mathop{\rm Br}} } _ {D} } &kC _ {G} ( D ) \\ | ||
| + | {} _ { { \mathop{\rm Tr} } _ {D,G } } \downarrow &{} & \downarrow _ { { \mathop{\rm Tr} } _ {D,N _ {G} ( D ) } } \\ | ||
| + | ( kG ) _ {D} ^ {G} & \mathop \rightarrow \limits _ { {{ \mathop{\rm Br}} } _ {D} } &kC _ {G} ( D ) _ {D} ^ {N _ {G} ( D ) } \\ | ||
| + | \end{array} | ||
| − | + | $$ | |
the top- and right-hand mappings are surjective, and hence so is the bottom mapping. It therefore induces the bijection of block idempotents described in the first main theorem. | the top- and right-hand mappings are surjective, and hence so is the bottom mapping. It therefore induces the bijection of block idempotents described in the first main theorem. | ||
| Line 27: | Line 107: | ||
In subsequent work, the Brauer homomorphism has been generalized to arbitrary modules: | In subsequent work, the Brauer homomorphism has been generalized to arbitrary modules: | ||
| − | + | $$ | |
| + | { { \mathop{\rm Br} } _ {D} } : {M ^ {D} } \rightarrow {M ^ {D} / \sum _ {D ^ \prime < D } M _ {D ^ \prime } ^ {D} } . | ||
| + | $$ | ||
| − | The concept is especially useful if | + | The concept is especially useful if $ M $ |
| + | is a $ G $- | ||
| + | algebra. L. Puig [[#References|[a5]]], [[#References|[a6]]] has developed an extensive theory of "interior G-algebras" , where $ G $ | ||
| + | is acting via inner automorphisms, and in which the Brauer homomorphism plays a central role. His work has had extensive impact both on module theory and on block theory, especially his classification of nilpotent blocks [[#References|[a7]]]. Further discussion of the Brauer homomorphism in this context can be found in [[#References|[a3]]] and [[#References|[a8]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Brauer, "Zur Darstellungstheorie der Gruppen endlicher Ordnung" ''Math. Z.'' , '''63''' (1956) pp. 406–441</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R. Brauer, "Zur Darstellungstheorie der Gruppen endlicher Ordnung II" ''Math. Z.'' , '''72''' (1959) pp. 25–46</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> B. Külshammer, "Lectures on block theory" , ''London Math. Soc. Lecture Notes Ser.'' , '''161''' , Cambridge Univ. Press (1991)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> H. Nagao, "A proof of Brauer's theorem on generalized decomposition numbers" ''Nagoya Math. J.'' , '''22''' (1963) pp. 73–77</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> L. Puig, "Pointed groups and construction of characters" ''Math. Z.'' , '''170''' (1981) pp. 265–292</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> L. Puig, "Pointed groups and construction of modules" ''J. Algebra'' , '''116''' (1988) pp. 7–129</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> L. Puig, "Nilpotent groups and their source algebras" ''Invent. Math.'' , '''93''' (1988) pp. 77–116</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> J. Thévenaz, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110860/b11086065.png" />-Algebras and modular representation theory" , ''Math. Monographs'' , Oxford Univ. Press (1995)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Brauer, "Zur Darstellungstheorie der Gruppen endlicher Ordnung" ''Math. Z.'' , '''63''' (1956) pp. 406–441</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R. Brauer, "Zur Darstellungstheorie der Gruppen endlicher Ordnung II" ''Math. Z.'' , '''72''' (1959) pp. 25–46</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> B. Külshammer, "Lectures on block theory" , ''London Math. Soc. Lecture Notes Ser.'' , '''161''' , Cambridge Univ. Press (1991)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> H. Nagao, "A proof of Brauer's theorem on generalized decomposition numbers" ''Nagoya Math. J.'' , '''22''' (1963) pp. 73–77</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> L. Puig, "Pointed groups and construction of characters" ''Math. Z.'' , '''170''' (1981) pp. 265–292</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> L. Puig, "Pointed groups and construction of modules" ''J. Algebra'' , '''116''' (1988) pp. 7–129</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> L. Puig, "Nilpotent groups and their source algebras" ''Invent. Math.'' , '''93''' (1988) pp. 77–116</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> J. Thévenaz, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110860/b11086065.png" />-Algebras and modular representation theory" , ''Math. Monographs'' , Oxford Univ. Press (1995)</TD></TR></table> | ||
Revision as of 06:29, 30 May 2020
The Brauer homomorphism was first used by R. Brauer [a1], [a2], and developed further by H. Nagao [a4] to establish a connection between the $ p $-
blocks of a finite group $ G $
and of the $ p $-
local subgroups (cf. Block). Subsequently, it has been used in a variety of other contexts within modular representation theory (cf. also Finite group, representation of a).
Let $ k $ be a field of characteristic $ p $, and let $ G $ act by conjugation on the group algebra $ kG $ with fixed points $ ( kG ) ^ {G} = Z ( kG ) $. The primitive idempotents $ e _ {0} \dots e _ {s} $ in $ Z ( kG ) $ correspond to the blocks $ B _ {0} \dots B _ {s} $ of $ kG $, so that $ B _ {i} = e _ {i} kG $ and $ kG = B _ {0} \oplus \dots \oplus B _ {s} $ as a direct sum of indecomposable two-sided ideals.
If $ H \leq K $ are subgroups of $ G $ and $ M $ is a $ kG $- module, there is a relative trace mapping $ { { \mathop{\rm Tr} } _ {H,K } } : {M ^ {H} } \rightarrow {M ^ {K} } $, given by $ m \mapsto \sum _ {i} g _ {i} m $, where $ g _ {i} $ runs through a set of coset representatives of $ H $ in $ K $. One writes $ M _ {H} ^ {K} $ for the image of $ { \mathop{\rm Tr} } _ {H,K } $. Applying this to the conjugation action of $ G $ on $ kG $, one says that $ D $ is a defect group for the block $ B _ {i} $( cf. also Defect group of a block) if $ e _ {i} $ lies in $ ( kG ) _ {D} ^ {G} $ but not in $ ( kG ) _ {D ^ \prime } ^ {D} $ for any proper subgroup $ D ^ \prime < D $. The defect groups of a block form a single conjugacy class of $ p $- subgroups of $ G $.
If $ D $ is any $ p $- subgroup of $ G $, still acting on $ G $ by conjugation, then there is a decomposition
$$ ( kG ) ^ {D} = kC _ {G} ( D ) \oplus \sum _ {D ^ \prime < D } ( kG ) _ {D ^ \prime } ^ {D} $$
as a direct sum of a subring and a two-sided ideal. This is because the left-hand side has as a basis the orbit sums. The orbits of length one span $ kC _ {G} ( D ) $, and the sums of orbits of length greater than one are transfers from proper subgroups of $ D $. The Brauer homomorphism
$$ { { \mathop{\rm Br} } _ {D} } : {( kG ) ^ {D} } \rightarrow {kC _ {G} ( D ) } $$
is the projection onto the first factor in the above decomposition. Restricting to $ Z ( kG ) = ( kG ) ^ {G} \subseteq ( kG ) ^ {D} $, one obtains the homomorphism
$$ { { \mathop{\rm Br} } _ {D} } : {Z ( kG ) } \rightarrow {Z ( kC _ {G} ( D ) ) } $$
originally considered by Brauer.
Brauer's first main theorem states that the Brauer homomorphism $ { \mathop{\rm Br} } _ {D} $ establishes a one-to-one correspondence between the blocks of $ G $ with defect group $ D $ and the blocks of $ N _ {G} ( D ) $ with defect group $ D $. To make sense of this, first observe that every idempotent in $ Z ( kN _ {G} ( D ) ) $ lies in $ Z ( kC _ {G} ( D ) ) $( because the other summand $ \sum _ {D ^ \prime < D } ( kN _ {G} ( D ) ) _ {D ^ \prime } ^ {D} $ is contained in the Jacobson radical $ J ( kN _ {G} ( D ) ) $). A block idempotent $ e _ {i} \in Z ( kG ) $ has defect group $ D $ if and only if $ e _ {i} \in ( kG ) _ {D} ^ {G} $ and $ { \mathop{\rm Br} } _ {D} ( e _ {i} ) \neq 0 $. In the commutative diagram
$$ \begin{array}{ccc} ( kG ) ^ {D} & \mathop \rightarrow \limits ^ { {{ \mathop{\rm Br}} } _ {D} } &kC _ {G} ( D ) \\ {} _ { { \mathop{\rm Tr} } _ {D,G } } \downarrow &{} & \downarrow _ { { \mathop{\rm Tr} } _ {D,N _ {G} ( D ) } } \\ ( kG ) _ {D} ^ {G} & \mathop \rightarrow \limits _ { {{ \mathop{\rm Br}} } _ {D} } &kC _ {G} ( D ) _ {D} ^ {N _ {G} ( D ) } \\ \end{array} $$
the top- and right-hand mappings are surjective, and hence so is the bottom mapping. It therefore induces the bijection of block idempotents described in the first main theorem.
In subsequent work, the Brauer homomorphism has been generalized to arbitrary modules:
$$ { { \mathop{\rm Br} } _ {D} } : {M ^ {D} } \rightarrow {M ^ {D} / \sum _ {D ^ \prime < D } M _ {D ^ \prime } ^ {D} } . $$
The concept is especially useful if $ M $ is a $ G $- algebra. L. Puig [a5], [a6] has developed an extensive theory of "interior G-algebras" , where $ G $ is acting via inner automorphisms, and in which the Brauer homomorphism plays a central role. His work has had extensive impact both on module theory and on block theory, especially his classification of nilpotent blocks [a7]. Further discussion of the Brauer homomorphism in this context can be found in [a3] and [a8].
References
| [a1] | R. Brauer, "Zur Darstellungstheorie der Gruppen endlicher Ordnung" Math. Z. , 63 (1956) pp. 406–441 |
| [a2] | R. Brauer, "Zur Darstellungstheorie der Gruppen endlicher Ordnung II" Math. Z. , 72 (1959) pp. 25–46 |
| [a3] | B. Külshammer, "Lectures on block theory" , London Math. Soc. Lecture Notes Ser. , 161 , Cambridge Univ. Press (1991) |
| [a4] | H. Nagao, "A proof of Brauer's theorem on generalized decomposition numbers" Nagoya Math. J. , 22 (1963) pp. 73–77 |
| [a5] | L. Puig, "Pointed groups and construction of characters" Math. Z. , 170 (1981) pp. 265–292 |
| [a6] | L. Puig, "Pointed groups and construction of modules" J. Algebra , 116 (1988) pp. 7–129 |
| [a7] | L. Puig, "Nilpotent groups and their source algebras" Invent. Math. , 93 (1988) pp. 77–116 |
| [a8] | J. Thévenaz, "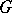 -Algebras and modular representation theory" , Math. Monographs , Oxford Univ. Press (1995) -Algebras and modular representation theory" , Math. Monographs , Oxford Univ. Press (1995) |
Brauer homomorphism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Brauer_homomorphism&oldid=46159