Difference between revisions of "Bernstein algebra"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | b1103401.png | ||
| + | $#A+1 = 58 n = 2 | ||
| + | $#C+1 = 58 : ~/encyclopedia/old_files/data/B110/B.1100340 Bernstein algebra | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | Around 1900, S.N. Bernstein (cf. [[#References|[a3]]], [[#References|[a4]]], [[#References|[a5]]]) worked on an important problem concerning the laws of formal genetics. This problem is known today as the Bernstein problem. Following Yu.I. Lyubich (cf. [[#References|[a10]]]), this problem can be expressed as follows. The state of a population in a given generation is described by a vector in $ \mathbf R ^ {n} $ | |
| + | whose coordinates satisfy $ x _ {i} \geq 0 $( | ||
| + | $ i = 1 \dots n $) | ||
| + | and $ \sum _ {i = 1 } ^ {n} x _ {i} = 1 $. | ||
| + | The set $ S $ | ||
| + | of all states is a simplex in $ \mathbf R ^ {n} $ | ||
| + | and the vertices $ e _ {i} $( | ||
| + | $ i = 1 \dots n $) | ||
| + | of $ S $ | ||
| + | are the different types of individuals in the population. If $ \gamma _ {ijk } $ | ||
| + | is the [[Probability|probability]] that an individual $ e _ {k} $ | ||
| + | appears in the next generation from parents of types $ e _ {i} $ | ||
| + | and $ e _ {j} $, | ||
| + | then $ \sum _ {k = 1 } ^ {n} \gamma _ {ijk } = 1 $( | ||
| + | $ i,j = 1 \dots n $) | ||
| + | and $ \gamma _ {ijk } = \gamma _ {jik } $( | ||
| + | $ i,j,k = 1 \dots n $). | ||
| + | In absence of selection and under random hypothesis, the state of the population in the next generation can be written, in terms of coordinates, as $ x _ {k} ^ \prime = \sum _ {i,j = 1 } ^ {n} \gamma _ {ijk } x _ {i} x _ {j} $( | ||
| + | $ k = 1 \dots n $). | ||
| + | These relations define a quadratic operator $ V : S \rightarrow S $ | ||
| + | called the evolutionary quadratic operator. The Bernstein stationarity principle says that $ V ^ {2} = V $ | ||
| + | and the Bernstein problem aims at describing all quadratic operators satisfying this principle. Bernstein solved his problem for $ n = 3 $ | ||
| + | and much progress was achieved recently (cf. [[#References|[a6]]], [[#References|[a8]]]) in this direction. The Bernstein problem can be translated in terms of algebra structure. In fact, over $ \mathbf R ^ {n} $ | ||
| + | an algebra structure can be defined via the operator $ V $ | ||
| + | by | ||
| + | |||
| + | $$ | ||
| + | xy = { | ||
| + | \frac{1}{2} | ||
| + | } ( V ( x + y ) - V ( x ) - V ( y ) ) | ||
| + | $$ | ||
| + | |||
| + | for all $ x, y \in \mathbf R ^ {n} $, | ||
| + | and if $ \omega : {\mathbf R ^ {n} } \rightarrow \mathbf R $ | ||
| + | is the mapping defined by $ x = ( x _ {1} \dots x _ {n} ) \mapsto \sum _ {i = 1 } ^ {n} x _ {i} $, | ||
| + | then $ V ^ {2} = V $ | ||
| + | if and only if $ ( x ^ {2} ) ^ {2} = \omega ( x ) ^ {2} x ^ {2} $ | ||
| + | for all $ x \in \mathbf R ^ {n} $. | ||
| + | Moreover, $ \omega ( xy ) = \omega ( x ) \omega ( y ) $ | ||
| + | for all $ x, y \in \mathbf R ^ {n} $. | ||
| + | Of course, to define this multiplication over the whole space $ \mathbf R ^ {n} $ | ||
| + | starting from the simplex $ S $, | ||
| + | one has to make convenient extensions of this multiplication by bilinearity. Now, in general, if $ K $ | ||
| + | is a (commutative) [[Field|field]] and $ A $ | ||
| + | is a commutative $ K $- | ||
| + | algebra, then a weighted algebra $ ( A, \omega ) $ | ||
| + | over $ K $ | ||
| + | is said to be a Bernstein algebra if $ ( x ^ {2} ) ^ {2} = \omega ( x ) ^ {2} x ^ {2} $ | ||
| + | for all $ x \in A $( | ||
| + | cf. [[#References|[a2]]]). In recent years (1990s), the theory of Bernstein algebras has been substantially improved. V.M. Abraham (cf. [[#References|[a1]]]) suggests the construction of a generalized Bernstein algebra. In this perspective, for an element $ x \in A $, | ||
| + | where $ ( A, \omega ) $ | ||
| + | is a weighted algebra, the plenary powers $ x ^ {[ m ] } $ | ||
| + | of $ x $ | ||
| + | are defined by $ x ^ {[ 1 ] } = x $ | ||
| + | and $ x ^ {[ m -1 ] } x ^ {[ m -1 ] } = x ^ {[ m ] } $ | ||
| + | for all integer $ m \geq 2 $. | ||
| + | The plenary powers can be interpreted by saying that they represent random mating between discrete non-overlapping generations. $ ( A, \omega ) $ | ||
| + | is called an $ n $ | ||
| + | th order Bernstein algebra if $ x ^ {[ n + 2 ] } = \omega ( x ) ^ {2 ^ {n} } x ^ {[ n + 1 ] } $ | ||
| + | for all $ x \in A $, | ||
| + | where $ n \geq 1 $ | ||
| + | is the smallest such integer (cf. [[#References|[a11]]]). Second-order Bernstein algebras are simply called Bernstein algebras and first-order Bernstein algebras are also called gametic diploid algebras. The interpretation of the equation $ x ^ {[ n + 2 ] } = x ^ {[ n + 1 ] } $( | ||
| + | $ x \in A $ | ||
| + | such that $ \omega ( x ) = 1 $) | ||
| + | is that equilibrium in the population is reached after exactly $ n $ | ||
| + | generations of intermixing. For genetic properties of Bernstein algebras, see [[#References|[a7]]] and [[#References|[a12]]]. | ||
See also [[Genetic algebra|Genetic algebra]]; [[Baric algebra|Baric algebra]]. | See also [[Genetic algebra|Genetic algebra]]; [[Baric algebra|Baric algebra]]. | ||
Revision as of 10:58, 29 May 2020
Around 1900, S.N. Bernstein (cf. [a3], [a4], [a5]) worked on an important problem concerning the laws of formal genetics. This problem is known today as the Bernstein problem. Following Yu.I. Lyubich (cf. [a10]), this problem can be expressed as follows. The state of a population in a given generation is described by a vector in $ \mathbf R ^ {n} $
whose coordinates satisfy $ x _ {i} \geq 0 $(
$ i = 1 \dots n $)
and $ \sum _ {i = 1 } ^ {n} x _ {i} = 1 $.
The set $ S $
of all states is a simplex in $ \mathbf R ^ {n} $
and the vertices $ e _ {i} $(
$ i = 1 \dots n $)
of $ S $
are the different types of individuals in the population. If $ \gamma _ {ijk } $
is the probability that an individual $ e _ {k} $
appears in the next generation from parents of types $ e _ {i} $
and $ e _ {j} $,
then $ \sum _ {k = 1 } ^ {n} \gamma _ {ijk } = 1 $(
$ i,j = 1 \dots n $)
and $ \gamma _ {ijk } = \gamma _ {jik } $(
$ i,j,k = 1 \dots n $).
In absence of selection and under random hypothesis, the state of the population in the next generation can be written, in terms of coordinates, as $ x _ {k} ^ \prime = \sum _ {i,j = 1 } ^ {n} \gamma _ {ijk } x _ {i} x _ {j} $(
$ k = 1 \dots n $).
These relations define a quadratic operator $ V : S \rightarrow S $
called the evolutionary quadratic operator. The Bernstein stationarity principle says that $ V ^ {2} = V $
and the Bernstein problem aims at describing all quadratic operators satisfying this principle. Bernstein solved his problem for $ n = 3 $
and much progress was achieved recently (cf. [a6], [a8]) in this direction. The Bernstein problem can be translated in terms of algebra structure. In fact, over $ \mathbf R ^ {n} $
an algebra structure can be defined via the operator $ V $
by
$$ xy = { \frac{1}{2} } ( V ( x + y ) - V ( x ) - V ( y ) ) $$
for all $ x, y \in \mathbf R ^ {n} $, and if $ \omega : {\mathbf R ^ {n} } \rightarrow \mathbf R $ is the mapping defined by $ x = ( x _ {1} \dots x _ {n} ) \mapsto \sum _ {i = 1 } ^ {n} x _ {i} $, then $ V ^ {2} = V $ if and only if $ ( x ^ {2} ) ^ {2} = \omega ( x ) ^ {2} x ^ {2} $ for all $ x \in \mathbf R ^ {n} $. Moreover, $ \omega ( xy ) = \omega ( x ) \omega ( y ) $ for all $ x, y \in \mathbf R ^ {n} $. Of course, to define this multiplication over the whole space $ \mathbf R ^ {n} $ starting from the simplex $ S $, one has to make convenient extensions of this multiplication by bilinearity. Now, in general, if $ K $ is a (commutative) field and $ A $ is a commutative $ K $- algebra, then a weighted algebra $ ( A, \omega ) $ over $ K $ is said to be a Bernstein algebra if $ ( x ^ {2} ) ^ {2} = \omega ( x ) ^ {2} x ^ {2} $ for all $ x \in A $( cf. [a2]). In recent years (1990s), the theory of Bernstein algebras has been substantially improved. V.M. Abraham (cf. [a1]) suggests the construction of a generalized Bernstein algebra. In this perspective, for an element $ x \in A $, where $ ( A, \omega ) $ is a weighted algebra, the plenary powers $ x ^ {[ m ] } $ of $ x $ are defined by $ x ^ {[ 1 ] } = x $ and $ x ^ {[ m -1 ] } x ^ {[ m -1 ] } = x ^ {[ m ] } $ for all integer $ m \geq 2 $. The plenary powers can be interpreted by saying that they represent random mating between discrete non-overlapping generations. $ ( A, \omega ) $ is called an $ n $ th order Bernstein algebra if $ x ^ {[ n + 2 ] } = \omega ( x ) ^ {2 ^ {n} } x ^ {[ n + 1 ] } $ for all $ x \in A $, where $ n \geq 1 $ is the smallest such integer (cf. [a11]). Second-order Bernstein algebras are simply called Bernstein algebras and first-order Bernstein algebras are also called gametic diploid algebras. The interpretation of the equation $ x ^ {[ n + 2 ] } = x ^ {[ n + 1 ] } $( $ x \in A $ such that $ \omega ( x ) = 1 $) is that equilibrium in the population is reached after exactly $ n $ generations of intermixing. For genetic properties of Bernstein algebras, see [a7] and [a12].
See also Genetic algebra; Baric algebra.
References
| [a1] | V.M. Abraham, "Linearising quadratic transformations in genetic algebras" Thesis, Univ. London (1975) |
| [a2] | M.T. Alcalde, C. Burgueno, A. Labra, A. Micali, "Sur les algèbres de Bernstein" Proc. London Math. Soc. (3) , 58 (1989) pp. 51–68 |
| [a3] | S.N. Bernstein, "Principe de stationarité et généralisation de la loi de Mendel" C.R. Acad. Sci. Paris , 177 (1923) pp. 528–531 |
| [a4] | S.N. Bernstein, "Démonstration mathématique de la loi d'hérédité de Mendel" C.R. Acad. Sci. Paris , 177 (1923) pp. 581–584 |
| [a5] | S.N. Bernstein, "Solution of a mathematical problem connected with the theory of heredity" Ann. Math. Stat. , 13 (1942) pp. 53–61 |
| [a6] | S. González, J.C. Gutiérrez, C. Martínez, "The Bernstein problem in dimension  " J. Algebra , 177 (1995) pp. 676–697 " J. Algebra , 177 (1995) pp. 676–697 |
| [a7] | A.N. Griskhov, "On the genetic property of Bernstein algebras" Soviet Math. Dokl. , 35 (1987) pp. 489–492 (In Russian) |
| [a8] | J.C. Gutiérrez, "The Bernstein problem for type 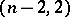 " J. Algebra , 181 (1996) pp. 613–627 " J. Algebra , 181 (1996) pp. 613–627 |
| [a9] | P. Holgate, "Genetic algebras satisfying Bernstein's stationarity principle" J. London Math. Soc. (2) , 9 (1975) pp. 613–623 |
| [a10] | Yu.I. Lyubich, "Mathematical structures in population genetics" Biomathematics , 22 (1992) |
| [a11] | C. Mallol, A. Micali, M. Ouattara, "Sur les algèbres de Bernstein IV" Linear Alg. & Its Appl. , 158 (1991) pp. 1–26 |
| [a12] | A. Micali, M. Ouattara, "Structure des algèbres de Bernstein" Linear Alg. & Its Appl. , 218 (1995) pp. 77–88 |
Bernstein algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bernstein_algebra&oldid=46025