Difference between revisions of "Area principle"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | a0132201.png | ||
| + | $#A+1 = 68 n = 1 | ||
| + | $#C+1 = 68 : ~/encyclopedia/old_files/data/A013/A.0103220 Area principle | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | The area of the complement to the image of a domain under a mapping by a function regular in it is non-negative. The area principle was first used in 1914 by T.H. Gronwall [[#References|[1]]], who in this way proved the so-called exterior area theorem for functions of class $ \Sigma $— | |
| + | functions | ||
| − | + | $$ | |
| + | F (z) = z + \alpha _ {0} + | ||
| + | \frac{\alpha _ {1} }{z} | ||
| + | + \dots , | ||
| + | $$ | ||
| + | |||
| + | that are regular and univalent in the annulus $ \Delta ^ \prime = \{ {z } : {1 < | z | < \infty } \} $( | ||
| + | cf. [[Univalent function|Univalent function]]). The area $ \sigma ( C F ( \Delta ^ \prime ) ) $ | ||
| + | of the complement of the image $ F ( \Delta ^ \prime ) $ | ||
| + | of $ \Delta ^ \prime $ | ||
| + | under a mapping $ w = F (z) \in \Sigma $ | ||
| + | can be determined by the formula | ||
| + | |||
| + | $$ | ||
| + | \sigma ( C F ( \Delta ^ \prime ) ) = \pi | ||
| + | \left ( | ||
| + | 1 - \sum _ { k=1 } ^ \infty | ||
| + | k | \alpha _ {k} | ^ {2} | ||
| + | \right ) | ||
| + | \geq 0 | ||
| + | $$ | ||
and consequently | and consequently | ||
| − | + | $$ \tag{1 } | |
| + | \sum _ { k=1 } ^ \infty | ||
| + | k | \alpha _ {k} | ^ {2} | ||
| + | \leq 1 . | ||
| + | $$ | ||
| − | By means of (1) the first results were obtained for functions of the classes | + | By means of (1) the first results were obtained for functions of the classes $ \Sigma $ |
| + | and $ S $, | ||
| + | where $ S $ | ||
| + | is the class of functions $ f (z) = z + \sum _ {k=2} ^ \infty a _ {k} z ^ {k} $ | ||
| + | that are regular and univalent in the disc $ \Delta = \{ {z } : {| z | < 1 } \} $( | ||
| + | cf. [[Bieberbach conjecture|Bieberbach conjecture]]; [[Distortion theorems|Distortion theorems]]). A more general area theorem has been proved [[#References|[2]]]. G.M. Goluzin [[#References|[3]]] extended the area theorem to $ p $- | ||
| + | valent functions in the disc (cf. [[Multivalent function|Multivalent function]]). | ||
| − | The following area theorem has been proved [[#References|[4]]]: Let | + | The following area theorem has been proved [[#References|[4]]]: Let $ F \in \Sigma $, |
| + | $ \overline{B}\; = C F ( \Delta ^ \prime ) $, | ||
| + | and let $ Q (w) $ | ||
| + | be a regular function in $ \overline{B}\; $. | ||
| + | If | ||
| − | + | $$ | |
| + | Q ( F (z) ) = \ | ||
| + | \sum _ {k = - \infty } ^ { {+ } \infty } | ||
| + | \alpha _ {k} z ^ {-k} | ||
| + | \not\equiv \textrm{ const } ; | ||
| + | $$ | ||
then | then | ||
| − | + | $$ \tag{2 } | |
| + | \sum _ {k = - \infty } ^ { {+ } \infty } | ||
| + | k | \alpha _ {k} | ^ {2} | ||
| + | \leq 0, | ||
| + | $$ | ||
| + | |||
| + | and equality holds only if the area $ \sigma ( \overline{B}\; ) $ | ||
| + | of $ \overline{B}\; $ | ||
| + | is zero. | ||
| + | |||
| + | By the area theorem for a certain class of univalent functions $ f (z) $, | ||
| + | $ z \in B $, | ||
| + | with $ B $ | ||
| + | a domain, one usually understands any inequality having the property that equality holds if and only if the area of the complement $ \overline{G}\; $ | ||
| + | of $ f (B) $ | ||
| + | is zero, and the same applies for a class of systems of univalent functions $ \{ {f _ {k} (z) } : {z \in B _ {k} } \} _ {k=0} ^ {n} , n = 1 , 2 \dots $ | ||
| + | where $ B _ {k} $ | ||
| + | is a domain and $ \overline{G}\; $ | ||
| + | is the complement of $ \cup _ {k=0} ^ {n} f _ {k} (B _ {f} ) $. | ||
| + | Usually, such a theorem is proved by means of the area principle. That is, one considers any regular function $ Q (w) $, | ||
| + | or more generally, one having a regular derivative, on $ \overline{G}\; $ | ||
| + | and calculates the area $ \sigma ( Q ( \overline{G}\; ) ) $ | ||
| + | of the image of $ \overline{G}\; $ | ||
| + | under the mapping of the function $ Q $. | ||
| + | Therefore, (2) is a certain extremely general area theorem in the class $ \Sigma $. | ||
| − | and | + | Let $ F \in \Sigma $ |
| + | and let | ||
| − | + | $$ | |
| + | \mathop{\rm ln} \ | ||
| − | + | \frac{F (t) - F (z) }{t - z } | |
| + | = \ | ||
| + | \sum _ { p,q=1 } ^ \infty | ||
| + | \omega _ {p,q} t ^ {-p} z ^ {-q} ,\ t , z \in \Delta ^ \prime . | ||
| + | $$ | ||
| − | + | One chooses a suitable function, regular in $ C F ( \Delta ^ \prime ) $, | |
| + | to be able to write (2) as | ||
| − | + | $$ \tag{3 } | |
| + | \sum _ { q=1 } ^ \infty | ||
| + | q \left | | ||
| + | \sum _ { p=1 } ^ \infty \omega _ {p,q} x _ {p} \right | ^ {2} | ||
| + | \leq \ | ||
| + | \sum _ { p=1 } ^ \infty | ||
| − | + | \frac{1}{p} | |
| + | \ | ||
| + | | x _ {p} | ^ {2} , | ||
| + | $$ | ||
| − | where the | + | where the $ x _ {p} $ |
| + | are any numbers not simultaneously equal to zero and such that | ||
| − | + | $$ | |
| + | \overline{\lim\limits}\; | ||
| + | _ {p \rightarrow \infty } \ | ||
| + | | x _ {p} | ^ {1/p} | ||
| + | < 1 . | ||
| + | $$ | ||
| − | More general area theorems in | + | More general area theorems in $ \Sigma $ |
| + | have also been obtained [[#References|[5]]]. | ||
| − | Area theorems have been proved for the following: the class | + | Area theorems have been proved for the following: the class $ \mathfrak M ( a _ {1} \dots a _ {n} ) $ |
| + | of systems $ \{ {f _ {k} (z) } : {f _ {k} (0) = a _ {k} , z \in \Delta } \} _ {k=1} ^ {n} $ | ||
| + | of functions $ f _ {k} $ | ||
| + | that map the disc $ \Delta $ | ||
| + | conformally and univalently onto domains without pairwise common points, i.e. onto non-adjacent domains [[#References|[6]]]; the class $ \Sigma (B) $( | ||
| + | $ \Sigma (B) $, | ||
| + | $ B \ni \infty $, | ||
| + | is the class of functions $ F $ | ||
| + | that are regular and univalent in $ B \setminus \{ \infty \} $ | ||
| + | and such that $ F ( \infty ) = \infty $, | ||
| + | $ \lim\limits _ {z \rightarrow \infty } {F (z) } / z = 1 $), | ||
| + | [[#References|[7]]]; and non-overlapping multiple-connected domains (see [[#References|[6]]] and also [[#References|[8]]], [[#References|[9]]]). All the area theorems for multiple-connected domains can be proved by the method of contour integration (cf. [[Contour integration, method of|Contour integration, method of]]). | ||
By the area method one understands methods of solving various problems in the theory of univalent functions by the use of area theorems. | By the area method one understands methods of solving various problems in the theory of univalent functions by the use of area theorems. | ||
| Line 45: | Line 150: | ||
For instance, from (3) one may obtain by means of the Cauchy inequality that | For instance, from (3) one may obtain by means of the Cauchy inequality that | ||
| − | + | $$ \tag{4 } | |
| + | \left | | ||
| + | \sum _ { p,q=1 } ^ \infty | ||
| + | \omega _ {p,q} x _ {p} x _ {q} ^ \prime | ||
| + | \right | ^ {2} | ||
| + | \leq \ | ||
| + | \sum _ { p=1 } ^ \infty | ||
| + | |||
| + | \frac{1}{p} | ||
| + | \ | ||
| + | | x _ {p} | ^ {2} | ||
| + | \sum _ { q=1 } ^ \infty | ||
| + | |||
| + | \frac{1}{q} | ||
| + | \ | ||
| + | | x _ {q} ^ \prime | ^ {2} , | ||
| + | $$ | ||
| + | |||
| + | where $ x _ {p} $ | ||
| + | and $ x _ {q} ^ \prime $ | ||
| + | are such that the series on the right-hand side converge. If in (4), for example, $ x _ {p} = t ^ {-p} $, | ||
| + | $ x _ {q} ^ \prime = z ^ {-q} $, | ||
| + | $ | t | > 1 $, | ||
| + | $ | z | > 1 $, | ||
| + | one obtains the chord-distortion theorem | ||
| + | |||
| + | $$ | ||
| + | \left | \mathop{\rm ln} \ | ||
| + | |||
| + | \frac{F (t) - F (z) }{t - z } | ||
| + | |||
| + | \right | ^ {2} | ||
| + | \leq \mathop{\rm ln} \ | ||
| − | + | \frac{| t | ^ {2} }{| t | ^ {2} -1 } | |
| + | \ | ||
| + | \mathop{\rm ln} \ | ||
| − | + | \frac{| z | ^ {2} }{| z | ^ {2} - 1 } | |
| + | . | ||
| + | $$ | ||
| − | Area theorems, for example in the class | + | Area theorems, for example in the class $ \mathfrak M ( a _ {1} \dots a _ {n} ) $, |
| + | give necessary and sufficient conditions for a system $ \{ {f _ {k} (z) } : {f _ {k} (0) = a _ {k} , z \in \Delta } \} _ {k=1} ^ {n} $ | ||
| + | of meromorphic functions $ f _ {k} $ | ||
| + | to belong to the class $ \mathfrak M ( a _ {1} \dots a _ {n} ) $( | ||
| + | see [[#References|[6]]], p. 179). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> T.H. Gronwall, "Some remarks on conformal representation" ''Ann. of Math. Ser. 2'' , '''16''' (1914 - 1915) pp. 72–76</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H. Prawitz, "Ueber Mittelwerte analytischer Funktionen" ''Arkiv. Mat. Astron., Fysik'' , '''20A''' : 6 (1927) pp. 1–12</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> G.M. Goluzin, "On <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013220/a01322069.png" />-valued functions" ''Math. Sb.'' , '''8''' : 2 (1940) pp. 277–284 (In Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> N.A. Lebedev, I.M. Milin, "On the coefficients of certain classes of analytic functions" ''Mat. Sb.'' , '''28''' : 2 (1951) pp. 359–400 (In Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> Z. Nehari, "Inequalities for the coefficients of univalent functions" ''Arch. Rational Mech. and Anal.'' , '''34''' : 4 (1969) pp. 301–330</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> N.A. Lebedev, "The area principle in the theory of univalent functions" , Moscow (1975) (In Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> I.M. Milin, "Univalent functions and orthonormal systems" , ''Transl. Math. Monogr.'' , '''49''' , Amer. Math. Soc. (1977) (Translated from Russian)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> Yu.E. Alenitsyn, "Area theorems for functions that are analytic in a finitely-connected domain" ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''37''' : 5 (1973) pp. 1132–1154 (In Russian)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> V.Ya. Gultyanskii, V.A. Shchepetov, "A general area theorem for a certain class of q-quasi-conformal mappings" ''Dokl. Akad. Nauk SSSR'' , '''218''' : 3 (1974) pp. 509–512 (In Russian)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> H. Grunsky, "Koeffizientenbedingungen für schlichtabbildender meromorphe Funktionen" ''Math. Z.'' , '''45''' : 1 (1939) pp. 29–61</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> T.H. Gronwall, "Some remarks on conformal representation" ''Ann. of Math. Ser. 2'' , '''16''' (1914 - 1915) pp. 72–76</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H. Prawitz, "Ueber Mittelwerte analytischer Funktionen" ''Arkiv. Mat. Astron., Fysik'' , '''20A''' : 6 (1927) pp. 1–12</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> G.M. Goluzin, "On <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013220/a01322069.png" />-valued functions" ''Math. Sb.'' , '''8''' : 2 (1940) pp. 277–284 (In Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> N.A. Lebedev, I.M. Milin, "On the coefficients of certain classes of analytic functions" ''Mat. Sb.'' , '''28''' : 2 (1951) pp. 359–400 (In Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> Z. Nehari, "Inequalities for the coefficients of univalent functions" ''Arch. Rational Mech. and Anal.'' , '''34''' : 4 (1969) pp. 301–330</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> N.A. Lebedev, "The area principle in the theory of univalent functions" , Moscow (1975) (In Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> I.M. Milin, "Univalent functions and orthonormal systems" , ''Transl. Math. Monogr.'' , '''49''' , Amer. Math. Soc. (1977) (Translated from Russian)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> Yu.E. Alenitsyn, "Area theorems for functions that are analytic in a finitely-connected domain" ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''37''' : 5 (1973) pp. 1132–1154 (In Russian)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> V.Ya. Gultyanskii, V.A. Shchepetov, "A general area theorem for a certain class of q-quasi-conformal mappings" ''Dokl. Akad. Nauk SSSR'' , '''218''' : 3 (1974) pp. 509–512 (In Russian)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> H. Grunsky, "Koeffizientenbedingungen für schlichtabbildender meromorphe Funktionen" ''Math. Z.'' , '''45''' : 1 (1939) pp. 29–61</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
Revision as of 18:48, 5 April 2020
The area of the complement to the image of a domain under a mapping by a function regular in it is non-negative. The area principle was first used in 1914 by T.H. Gronwall [1], who in this way proved the so-called exterior area theorem for functions of class $ \Sigma $—
functions
$$ F (z) = z + \alpha _ {0} + \frac{\alpha _ {1} }{z} + \dots , $$
that are regular and univalent in the annulus $ \Delta ^ \prime = \{ {z } : {1 < | z | < \infty } \} $( cf. Univalent function). The area $ \sigma ( C F ( \Delta ^ \prime ) ) $ of the complement of the image $ F ( \Delta ^ \prime ) $ of $ \Delta ^ \prime $ under a mapping $ w = F (z) \in \Sigma $ can be determined by the formula
$$ \sigma ( C F ( \Delta ^ \prime ) ) = \pi \left ( 1 - \sum _ { k=1 } ^ \infty k | \alpha _ {k} | ^ {2} \right ) \geq 0 $$
and consequently
$$ \tag{1 } \sum _ { k=1 } ^ \infty k | \alpha _ {k} | ^ {2} \leq 1 . $$
By means of (1) the first results were obtained for functions of the classes $ \Sigma $ and $ S $, where $ S $ is the class of functions $ f (z) = z + \sum _ {k=2} ^ \infty a _ {k} z ^ {k} $ that are regular and univalent in the disc $ \Delta = \{ {z } : {| z | < 1 } \} $( cf. Bieberbach conjecture; Distortion theorems). A more general area theorem has been proved [2]. G.M. Goluzin [3] extended the area theorem to $ p $- valent functions in the disc (cf. Multivalent function).
The following area theorem has been proved [4]: Let $ F \in \Sigma $, $ \overline{B}\; = C F ( \Delta ^ \prime ) $, and let $ Q (w) $ be a regular function in $ \overline{B}\; $. If
$$ Q ( F (z) ) = \ \sum _ {k = - \infty } ^ { {+ } \infty } \alpha _ {k} z ^ {-k} \not\equiv \textrm{ const } ; $$
then
$$ \tag{2 } \sum _ {k = - \infty } ^ { {+ } \infty } k | \alpha _ {k} | ^ {2} \leq 0, $$
and equality holds only if the area $ \sigma ( \overline{B}\; ) $ of $ \overline{B}\; $ is zero.
By the area theorem for a certain class of univalent functions $ f (z) $, $ z \in B $, with $ B $ a domain, one usually understands any inequality having the property that equality holds if and only if the area of the complement $ \overline{G}\; $ of $ f (B) $ is zero, and the same applies for a class of systems of univalent functions $ \{ {f _ {k} (z) } : {z \in B _ {k} } \} _ {k=0} ^ {n} , n = 1 , 2 \dots $ where $ B _ {k} $ is a domain and $ \overline{G}\; $ is the complement of $ \cup _ {k=0} ^ {n} f _ {k} (B _ {f} ) $. Usually, such a theorem is proved by means of the area principle. That is, one considers any regular function $ Q (w) $, or more generally, one having a regular derivative, on $ \overline{G}\; $ and calculates the area $ \sigma ( Q ( \overline{G}\; ) ) $ of the image of $ \overline{G}\; $ under the mapping of the function $ Q $. Therefore, (2) is a certain extremely general area theorem in the class $ \Sigma $.
Let $ F \in \Sigma $ and let
$$ \mathop{\rm ln} \ \frac{F (t) - F (z) }{t - z } = \ \sum _ { p,q=1 } ^ \infty \omega _ {p,q} t ^ {-p} z ^ {-q} ,\ t , z \in \Delta ^ \prime . $$
One chooses a suitable function, regular in $ C F ( \Delta ^ \prime ) $, to be able to write (2) as
$$ \tag{3 } \sum _ { q=1 } ^ \infty q \left | \sum _ { p=1 } ^ \infty \omega _ {p,q} x _ {p} \right | ^ {2} \leq \ \sum _ { p=1 } ^ \infty \frac{1}{p} \ | x _ {p} | ^ {2} , $$
where the $ x _ {p} $ are any numbers not simultaneously equal to zero and such that
$$ \overline{\lim\limits}\; _ {p \rightarrow \infty } \ | x _ {p} | ^ {1/p} < 1 . $$
More general area theorems in $ \Sigma $ have also been obtained [5].
Area theorems have been proved for the following: the class $ \mathfrak M ( a _ {1} \dots a _ {n} ) $ of systems $ \{ {f _ {k} (z) } : {f _ {k} (0) = a _ {k} , z \in \Delta } \} _ {k=1} ^ {n} $ of functions $ f _ {k} $ that map the disc $ \Delta $ conformally and univalently onto domains without pairwise common points, i.e. onto non-adjacent domains [6]; the class $ \Sigma (B) $( $ \Sigma (B) $, $ B \ni \infty $, is the class of functions $ F $ that are regular and univalent in $ B \setminus \{ \infty \} $ and such that $ F ( \infty ) = \infty $, $ \lim\limits _ {z \rightarrow \infty } {F (z) } / z = 1 $), [7]; and non-overlapping multiple-connected domains (see [6] and also [8], [9]). All the area theorems for multiple-connected domains can be proved by the method of contour integration (cf. Contour integration, method of).
By the area method one understands methods of solving various problems in the theory of univalent functions by the use of area theorems.
For instance, from (3) one may obtain by means of the Cauchy inequality that
$$ \tag{4 } \left | \sum _ { p,q=1 } ^ \infty \omega _ {p,q} x _ {p} x _ {q} ^ \prime \right | ^ {2} \leq \ \sum _ { p=1 } ^ \infty \frac{1}{p} \ | x _ {p} | ^ {2} \sum _ { q=1 } ^ \infty \frac{1}{q} \ | x _ {q} ^ \prime | ^ {2} , $$
where $ x _ {p} $ and $ x _ {q} ^ \prime $ are such that the series on the right-hand side converge. If in (4), for example, $ x _ {p} = t ^ {-p} $, $ x _ {q} ^ \prime = z ^ {-q} $, $ | t | > 1 $, $ | z | > 1 $, one obtains the chord-distortion theorem
$$ \left | \mathop{\rm ln} \ \frac{F (t) - F (z) }{t - z } \right | ^ {2} \leq \mathop{\rm ln} \ \frac{| t | ^ {2} }{| t | ^ {2} -1 } \ \mathop{\rm ln} \ \frac{| z | ^ {2} }{| z | ^ {2} - 1 } . $$
Area theorems, for example in the class $ \mathfrak M ( a _ {1} \dots a _ {n} ) $, give necessary and sufficient conditions for a system $ \{ {f _ {k} (z) } : {f _ {k} (0) = a _ {k} , z \in \Delta } \} _ {k=1} ^ {n} $ of meromorphic functions $ f _ {k} $ to belong to the class $ \mathfrak M ( a _ {1} \dots a _ {n} ) $( see [6], p. 179).
References
| [1] | T.H. Gronwall, "Some remarks on conformal representation" Ann. of Math. Ser. 2 , 16 (1914 - 1915) pp. 72–76 |
| [2] | H. Prawitz, "Ueber Mittelwerte analytischer Funktionen" Arkiv. Mat. Astron., Fysik , 20A : 6 (1927) pp. 1–12 |
| [3] | G.M. Goluzin, "On 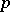 -valued functions" Math. Sb. , 8 : 2 (1940) pp. 277–284 (In Russian) -valued functions" Math. Sb. , 8 : 2 (1940) pp. 277–284 (In Russian) |
| [4] | N.A. Lebedev, I.M. Milin, "On the coefficients of certain classes of analytic functions" Mat. Sb. , 28 : 2 (1951) pp. 359–400 (In Russian) |
| [5] | Z. Nehari, "Inequalities for the coefficients of univalent functions" Arch. Rational Mech. and Anal. , 34 : 4 (1969) pp. 301–330 |
| [6] | N.A. Lebedev, "The area principle in the theory of univalent functions" , Moscow (1975) (In Russian) |
| [7] | I.M. Milin, "Univalent functions and orthonormal systems" , Transl. Math. Monogr. , 49 , Amer. Math. Soc. (1977) (Translated from Russian) |
| [8] | Yu.E. Alenitsyn, "Area theorems for functions that are analytic in a finitely-connected domain" Izv. Akad. Nauk SSSR Ser. Mat. , 37 : 5 (1973) pp. 1132–1154 (In Russian) |
| [9] | V.Ya. Gultyanskii, V.A. Shchepetov, "A general area theorem for a certain class of q-quasi-conformal mappings" Dokl. Akad. Nauk SSSR , 218 : 3 (1974) pp. 509–512 (In Russian) |
| [10] | H. Grunsky, "Koeffizientenbedingungen für schlichtabbildender meromorphe Funktionen" Math. Z. , 45 : 1 (1939) pp. 29–61 |
Comments
The inequalities (3) and (4) are a form of the Grunsky inequalities.
References
| [a1] | P.L. Duren, "Univalent functions" , Springer (1983) pp. Chapt. 10 |
Area principle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Area_principle&oldid=45215