|
|
| Line 1: |
Line 1: |
| | + | <!-- |
| | + | a1106201.png |
| | + | $#A+1 = 60 n = 1 |
| | + | $#C+1 = 60 : ~/encyclopedia/old_files/data/A110/A.1100620 Anti\AAhde Sitter space, |
| | + | Automatically converted into TeX, above some diagnostics. |
| | + | Please remove this comment and the {{TEX|auto}} line below, |
| | + | if TeX found to be correct. |
| | + | --> |
| | + | |
| | + | {{TEX|auto}} |
| | + | {{TEX|done}} |
| | + | |
| | ''complete maximal space-like hypersurfaces in an'' | | ''complete maximal space-like hypersurfaces in an'' |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a1106201.png" /> be an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a1106202.png" />-dimensional [[Minkowski space|Minkowski space]] of index <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a1106203.png" />, i.e., <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a1106204.png" /> and is equipped with the Lorentz metric <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a1106205.png" />. For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a1106206.png" />, let | + | Let $ \mathbf R _ {p + 1 } ^ {n + p + 1 } $ |
| | + | be an $ ( n + p + 1 ) $- |
| | + | dimensional [[Minkowski space|Minkowski space]] of index $ p + 1 $, |
| | + | i.e., $ \mathbf R _ {p + 1 } ^ {n + p + 1 } = \{ ( x _ {1} \dots x _ {n + p + 1 } ) \in \mathbf R ^ {n + p + 1 } \} $ |
| | + | and is equipped with the Lorentz metric $ \sum _ {i = 1 } ^ {n} ( dx _ {i} ) ^ {2} - \sum _ {j = 1 } ^ {p + 1 } ( dx _ {n + j } ) ^ {2} $. |
| | + | For $ c > 0 $, |
| | + | let |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a1106207.png" /></td> </tr></table>
| + | $$ |
| | + | H _ {p} ^ {n + p } ( c ) = \{ {x \in \mathbf R _ {p + 1 } ^ {n + p + 1 } } |
| | + | : |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a1106208.png" /></td> </tr></table>
| + | $$ |
| | + | \ |
| | + | {} {x _ {1} ^ {2} + \dots + x _ {n} ^ {2} - x _ {n + 1 } ^ {2} - \dots - x _ {n + p + 1 } ^ {2} = - {1 / c } } \} . |
| | + | $$ |
| | | | |
| − | Thus, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a1106209.png" /> is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062010.png" />-dimensional indefinite [[Riemannian manifold|Riemannian manifold]] of index <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062011.png" /> and of constant [[Curvature|curvature]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062012.png" />. It is called an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062013.png" />-dimensional anti-de Sitter space of constant curvature <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062014.png" /> and of index <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062015.png" />. A hypersurface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062016.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062017.png" /> is said to be space-like if the metric on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062018.png" /> induced by that of ambient space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062019.png" /> is positive definite. The mean curvature <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062020.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062021.png" /> is defined as in the case of Riemannian manifolds. By definition, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062022.png" /> is a maximal hypersurface if the mean curvature <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062023.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062024.png" /> is identically zero. S. Ishihara proved that a complete maximal space-like hypersurface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062025.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062026.png" /> satisfies <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062027.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062028.png" /> if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062029.png" /> is isometric to the hyperbolic cylinder <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062030.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062031.png" /> is the squared norm of the [[Second fundamental form|second fundamental form]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062032.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062033.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062034.png" />, is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062035.png" />-dimensional hyperbolic space of constant curvature <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062036.png" />. The rigidity of the hyperbolic cylinder <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062037.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062038.png" /> was proved by U.-H. Ki, H.S. Kim and H. Nakagawa [[#References|[a3]]]: for a given integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062039.png" /> and constant <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062040.png" />, there exists a constant <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062041.png" />, depending on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062042.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062043.png" />, such that the hyperbolic cylinder <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062044.png" /> is the only complete maximal space-like hypersurface in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062045.png" /> of constant scalar curvature and such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062046.png" />. In particular, for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062047.png" />, Q.M. Cheng [[#References|[a1]]] has characterized the complete maximal space-like hypersurfaces in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062048.png" /> under the condition of constant Gauss–Kronecker curvature (cf. [[Gaussian curvature|Gaussian curvature]]): Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062049.png" /> be a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062050.png" />-dimensional complete maximal space-like hypersurface of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062051.png" />. Now: | + | Thus, $ H _ {p} ^ {n + p } ( c ) $ |
| | + | is an $ ( n + p ) $- |
| | + | dimensional indefinite [[Riemannian manifold|Riemannian manifold]] of index $ p $ |
| | + | and of constant [[Curvature|curvature]] $ - c $. |
| | + | It is called an $ ( n + p ) $- |
| | + | dimensional anti-de Sitter space of constant curvature $ - c $ |
| | + | and of index $ p $. |
| | + | A hypersurface $ M $ |
| | + | of $ H _ {1} ^ {n + 1 } ( c ) $ |
| | + | is said to be space-like if the metric on $ M $ |
| | + | induced by that of ambient space $ H _ {1} ^ {n + 1 } ( c ) $ |
| | + | is positive definite. The mean curvature $ H $ |
| | + | of $ M $ |
| | + | is defined as in the case of Riemannian manifolds. By definition, $ M $ |
| | + | is a maximal hypersurface if the mean curvature $ H $ |
| | + | of $ M $ |
| | + | is identically zero. S. Ishihara proved that a complete maximal space-like hypersurface $ M $ |
| | + | in $ H _ {1} ^ {n + 1 } ( c ) $ |
| | + | satisfies $ S \leq nc $, |
| | + | and $ S = nc $ |
| | + | if and only if $ M $ |
| | + | is isometric to the hyperbolic cylinder $ H ^ {k} ( c _ {1} ) \times H ^ {n - k } ( c _ {2} ) $, |
| | + | where $ S $ |
| | + | is the squared norm of the [[Second fundamental form|second fundamental form]] of $ M $ |
| | + | and $ H ^ {k} ( c _ {i} ) $, |
| | + | $ i = 1, 2 $, |
| | + | is a $ k $- |
| | + | dimensional hyperbolic space of constant curvature $ c _ {i} $. |
| | + | The rigidity of the hyperbolic cylinder $ H ^ {k} ( c _ {1} ) \times H ^ {n - k } ( c _ {2} ) $ |
| | + | in $ H _ {1} ^ {n + 1 } ( c ) $ |
| | + | was proved by U.-H. Ki, H.S. Kim and H. Nakagawa [[#References|[a3]]]: for a given integer $ n $ |
| | + | and constant $ c > 0 $, |
| | + | there exists a constant $ C < nc $, |
| | + | depending on $ n $ |
| | + | and $ c $, |
| | + | such that the hyperbolic cylinder $ H ^ {k} ( c _ {1} ) \times H ^ {n - k } ( c _ {2} ) $ |
| | + | is the only complete maximal space-like hypersurface in $ H _ {1} ^ {n + 1 } ( c ) $ |
| | + | of constant scalar curvature and such that $ S > C $. |
| | + | In particular, for $ n = 3 $, |
| | + | Q.M. Cheng [[#References|[a1]]] has characterized the complete maximal space-like hypersurfaces in $ H _ {1} ^ {4} ( c ) $ |
| | + | under the condition of constant Gauss–Kronecker curvature (cf. [[Gaussian curvature|Gaussian curvature]]): Let $ M $ |
| | + | be a $ 3 $- |
| | + | dimensional complete maximal space-like hypersurface of $ H _ {1} ^ {4} ( c ) $. |
| | + | Now: |
| | | | |
| − | 1) if the Gauss–Kronecker curvature of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062052.png" /> is a non-zero constant, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062053.png" /> is the hyperbolic cylinder <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062054.png" />; | + | 1) if the Gauss–Kronecker curvature of $ M $ |
| | + | is a non-zero constant, then $ M $ |
| | + | is the hyperbolic cylinder $ H ^ {1} ( c _ {1} ) \times H ^ {2} ( c _ {2} ) $; |
| | | | |
| − | 2) if the [[Scalar curvature|scalar curvature]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062055.png" /> is constant and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062056.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062057.png" /> is the hyperbolic cylinder <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062058.png" />. There are no complete maximal space-like hypersurfaces in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062059.png" /> with constant scalar curvature and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110620/a11062060.png" />. | + | 2) if the [[Scalar curvature|scalar curvature]] $ K $ |
| | + | is constant and $ \inf K ^ {2} > 0 $, |
| | + | then $ M $ |
| | + | is the hyperbolic cylinder $ H ^ {1} ( c _ {1} ) \times H ^ {2} ( c _ {2} ) $. |
| | + | There are no complete maximal space-like hypersurfaces in $ H _ {1} ^ {4} ( c ) $ |
| | + | with constant scalar curvature and $ \sup K ^ {2} < { {S ^ {3} } / {54 } } $. |
| | | | |
| | On the other hand, complete space-like submanifolds in anti-de Sitter spaces with parallel mean curvature have been investigated by many authors. | | On the other hand, complete space-like submanifolds in anti-de Sitter spaces with parallel mean curvature have been investigated by many authors. |
complete maximal space-like hypersurfaces in an
Let $ \mathbf R _ {p + 1 } ^ {n + p + 1 } $
be an $ ( n + p + 1 ) $-
dimensional Minkowski space of index $ p + 1 $,
i.e., $ \mathbf R _ {p + 1 } ^ {n + p + 1 } = \{ ( x _ {1} \dots x _ {n + p + 1 } ) \in \mathbf R ^ {n + p + 1 } \} $
and is equipped with the Lorentz metric $ \sum _ {i = 1 } ^ {n} ( dx _ {i} ) ^ {2} - \sum _ {j = 1 } ^ {p + 1 } ( dx _ {n + j } ) ^ {2} $.
For $ c > 0 $,
let
$$
H _ {p} ^ {n + p } ( c ) = \{ {x \in \mathbf R _ {p + 1 } ^ {n + p + 1 } }
:
$$
$$
\
{} {x _ {1} ^ {2} + \dots + x _ {n} ^ {2} - x _ {n + 1 } ^ {2} - \dots - x _ {n + p + 1 } ^ {2} = - {1 / c } } \} .
$$
Thus, $ H _ {p} ^ {n + p } ( c ) $
is an $ ( n + p ) $-
dimensional indefinite Riemannian manifold of index $ p $
and of constant curvature $ - c $.
It is called an $ ( n + p ) $-
dimensional anti-de Sitter space of constant curvature $ - c $
and of index $ p $.
A hypersurface $ M $
of $ H _ {1} ^ {n + 1 } ( c ) $
is said to be space-like if the metric on $ M $
induced by that of ambient space $ H _ {1} ^ {n + 1 } ( c ) $
is positive definite. The mean curvature $ H $
of $ M $
is defined as in the case of Riemannian manifolds. By definition, $ M $
is a maximal hypersurface if the mean curvature $ H $
of $ M $
is identically zero. S. Ishihara proved that a complete maximal space-like hypersurface $ M $
in $ H _ {1} ^ {n + 1 } ( c ) $
satisfies $ S \leq nc $,
and $ S = nc $
if and only if $ M $
is isometric to the hyperbolic cylinder $ H ^ {k} ( c _ {1} ) \times H ^ {n - k } ( c _ {2} ) $,
where $ S $
is the squared norm of the second fundamental form of $ M $
and $ H ^ {k} ( c _ {i} ) $,
$ i = 1, 2 $,
is a $ k $-
dimensional hyperbolic space of constant curvature $ c _ {i} $.
The rigidity of the hyperbolic cylinder $ H ^ {k} ( c _ {1} ) \times H ^ {n - k } ( c _ {2} ) $
in $ H _ {1} ^ {n + 1 } ( c ) $
was proved by U.-H. Ki, H.S. Kim and H. Nakagawa [a3]: for a given integer $ n $
and constant $ c > 0 $,
there exists a constant $ C < nc $,
depending on $ n $
and $ c $,
such that the hyperbolic cylinder $ H ^ {k} ( c _ {1} ) \times H ^ {n - k } ( c _ {2} ) $
is the only complete maximal space-like hypersurface in $ H _ {1} ^ {n + 1 } ( c ) $
of constant scalar curvature and such that $ S > C $.
In particular, for $ n = 3 $,
Q.M. Cheng [a1] has characterized the complete maximal space-like hypersurfaces in $ H _ {1} ^ {4} ( c ) $
under the condition of constant Gauss–Kronecker curvature (cf. Gaussian curvature): Let $ M $
be a $ 3 $-
dimensional complete maximal space-like hypersurface of $ H _ {1} ^ {4} ( c ) $.
Now:
1) if the Gauss–Kronecker curvature of $ M $
is a non-zero constant, then $ M $
is the hyperbolic cylinder $ H ^ {1} ( c _ {1} ) \times H ^ {2} ( c _ {2} ) $;
2) if the scalar curvature $ K $
is constant and $ \inf K ^ {2} > 0 $,
then $ M $
is the hyperbolic cylinder $ H ^ {1} ( c _ {1} ) \times H ^ {2} ( c _ {2} ) $.
There are no complete maximal space-like hypersurfaces in $ H _ {1} ^ {4} ( c ) $
with constant scalar curvature and $ \sup K ^ {2} < { {S ^ {3} } / {54 } } $.
On the other hand, complete space-like submanifolds in anti-de Sitter spaces with parallel mean curvature have been investigated by many authors.
Cf. also De Sitter space.
References
| [a1] | Q.M. Cheng, "Complete maximal space-like hypersurfaces of 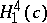 " Manuscr. Math. , 82 (1994) pp. 149–160 " Manuscr. Math. , 82 (1994) pp. 149–160 |
| [a2] | T. Ishikawa, "Maximal space-like submanifolds of a pseudo–Riemannian space of constant curvature" Michigan Math. J. , 35 (1988) pp. 345–352 |
| [a3] | U-H. Ki, H.S. Kim, H. Nakagawa, "Complete maximal space-like hypersurfaces of an anti-de Sitter space" Kyungpook Math. J. , 31 (1991) pp. 131–141 |
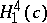 " Manuscr. Math. , 82 (1994) pp. 149–160
" Manuscr. Math. , 82 (1994) pp. 149–160