Difference between revisions of "Abel theorem"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (tex done) |
||
| Line 1: | Line 1: | ||
| − | Abel's theorem on algebraic equations: Formulas expressing the solution of an arbitrary equation of degree | + | {{TEX|done}} |
| + | |||
| + | Abel's theorem on algebraic equations: Formulas expressing the solution of an arbitrary equation of degree $ n $ | ||
| + | in terms of its coefficients using radicals do not exist for any $ n \geq 5 $. | ||
| + | The theorem was proved by N.H. Abel in 1824 . Abel's theorem may also be obtained as a corollary of [[Galois theory|Galois theory]], from which a more general theorem follows: For any $ n \geq 5 $ | ||
| + | there exist algebraic equations with integer coefficients whose roots cannot be expressed in terms of radicals of rational numbers. For a modern formulation of Abel's theorem for equations over an arbitrary field, see [[Algebraic equation|Algebraic equation]]. | ||
Abel's theorem on power series: If the power series | Abel's theorem on power series: If the power series | ||
| − | + | $$ \tag{*} | |
| + | S ( z ) \ = \ \sum _ {k = 0} ^ \infty a _ {k} ( z - b ) ^ {k} , | ||
| + | $$ | ||
| − | where | + | where $ a _ {k} ,\ b,\ z $ |
| + | are complex numbers, converges at $ z = z _ {0} $, | ||
| + | then it converges absolutely and uniformly within any disc $ | z - b | \leq \rho $ | ||
| + | of radius $ \rho < | z _ {0} - b | $ | ||
| + | and with centre at $ b $. | ||
| + | The theorem was established by N.H. Abel . It follows from the theorem that there exists a number $ R \in [ 0,\ \infty ] $ | ||
| + | such that if $ | z - b | < R $ | ||
| + | the series is convergent, while if $ | z - b | > R $ | ||
| + | the series is divergent. The number $ R $ | ||
| + | is called the radius of convergence of the series (*), while the disc $ | z - b | < R $ | ||
| + | is known as the disc of convergence of the series (*). | ||
Abel's continuity theorem: If the power series | Abel's continuity theorem: If the power series | ||
| − | converges at a point | + | converges at a point $ z _ {0} $ |
| + | on the boundary of the disc of convergence, then it is a continuous function in any closed triangle $ T $ | ||
| + | with vertices $ z _ {0} ,\ z _ {1} ,\ z _ {2} $, | ||
| + | where $ z _ {1} ,\ z _ {2} $ | ||
| + | are located inside the disc of convergence. In particular | ||
| − | + | $$ | |
| + | \lim\limits _ {\begin{array}{c} | ||
| + | z \rightarrow z _ {0} , \\ | ||
| + | z \in T | ||
| + | \end{array} | ||
| + | } \ | ||
| + | S ( z ) \ = \ S ( z _ {0} ) . | ||
| + | $$ | ||
This limit always exists along the radius: The series | This limit always exists along the radius: The series | ||
| − | converges uniformly along any radius of the disc of convergence joining the points | + | converges uniformly along any radius of the disc of convergence joining the points $ b $ |
| + | and $ z _ {0} $. | ||
| + | This theorem is used, in particular, to calculate the sum of a power series which converges at the boundary points of the disc of convergence. | ||
Abel's theorem on Dirichlet series: If the [[Dirichlet series|Dirichlet series]] | Abel's theorem on Dirichlet series: If the [[Dirichlet series|Dirichlet series]] | ||
| − | + | $$ | |
| + | \phi ( s ) \ = \ \sum _ {n = 1} ^ \infty | ||
| + | a _ {n} e ^ {- \lambda _ {n} s} , | ||
| + | \ \ s = \sigma + it ,\ \ \lambda _ {n} > 0 , | ||
| + | $$ | ||
| − | converges at the point | + | converges at the point $ s _ {0} = \sigma _ {0} + i t _ {0} $, |
| + | then it converges in the half-plane $ \sigma > \sigma _ {0} $ | ||
| + | and converges uniformly inside any angle $ | \mathop{\rm arg} (s - s _ {0} ) | \leq \theta < \pi / 2 $. | ||
| + | It is a generalization of Abel's theorem on power series (take $ \lambda _ {n} = n $ | ||
| + | and put $ e ^ {-s} = z $). | ||
| + | It follows from the theorem that the domain of convergence of a Dirichlet series is some half-plane $ \sigma > c $, | ||
| + | where $ c $ | ||
| + | is the abscissa of convergence of the series. | ||
| − | The following theorem is valid for an ordinary Dirichlet series (when | + | The following theorem is valid for an ordinary Dirichlet series (when $ \lambda _ {n} = \mathop{\rm ln} \ n $) |
| + | with a known asymptotic behaviour for the sum-function $ A _ {n} = a _ {1} + \dots + a _ {n} $ | ||
| + | of the coefficients of the series: If | ||
| − | + | $$ | |
| + | A _ {n} \ = \ B \ n ^ {s _ 1} ( \mathop{\rm ln} \ n ) ^ \alpha | ||
| + | + O ( n ^ \beta ) , | ||
| + | $$ | ||
| − | where | + | where $ B ,\ s _ {1} ,\ \alpha $ |
| + | are complex numbers, $ \beta $ | ||
| + | is a real number, $ \sigma _ {1} - 1 < \beta < \sigma _ {1} $, | ||
| + | $ \sigma _ {1} = \mathop{\rm Re} \ s _ {1} $, | ||
| + | then the Dirichlet series converges for $ \sigma _ {1} < \sigma $, | ||
| + | and the function $ \phi (s) $ | ||
| + | can be regularly extended to the half-plane $ \beta < \sigma $ | ||
| + | with the exception of the point $ s = s _ {1} $. | ||
| + | Moreover | ||
| − | + | $$ | |
| + | \phi ( s ) \ = \ B \ \Gamma ( \alpha + 1 ) s ( s - s _ {1} ) ^ {- \alpha - 1} + g ( s ) | ||
| + | $$ | ||
| − | if | + | if $ \alpha \neq -1,\ -2 \dots $ |
| + | and | ||
| − | + | $$ | |
| + | \phi ( s ) \ = \ B | ||
| + | \frac{( - 1 ) ^ {- \alpha}}{( - \alpha - 1 ) !} | ||
| + | s ( s - s _ {1} ) ^ {- \alpha - 1} \ | ||
| + | \mathop{\rm ln} ( s - s _ {1} ) + g ( s ) | ||
| + | $$ | ||
| − | if | + | if $ \alpha = -1,\ -2 ,\dots $. |
| + | Here $ g(s) $ | ||
| + | is a regular function for $ \sigma > \beta $. | ||
| − | E.g., the Riemann zeta-function | + | E.g., the Riemann zeta-function $ \zeta (s) $( |
| + | $ A _ {n} = n $, | ||
| + | $ B = 1 $, | ||
| + | $ s _ {1} = 1 $, | ||
| + | $ \alpha = 0 $, | ||
| + | $ \beta > 0 $) | ||
| + | is regular at least in the half-plane $ \sigma > 0 $, | ||
| + | with the exception of the point $ s = 1 $ | ||
| + | at which it has a first-order pole with residue $ 1 $. | ||
| + | This theorem can be generalized in various ways. E.g., if | ||
| − | + | $$ | |
| + | A _ {n} \ = \ \sum _ {j = 1} ^ { k } B _ {j} n ^ {s _ j} | ||
| + | ( \mathop{\rm ln} \ n ) ^ {\alpha _ j} + O ( n ^ \beta ) , | ||
| + | $$ | ||
| − | where | + | where $ B _ {j} ,\ s _ {j} ,\ \alpha _ {j} $( |
| + | $ 1 \leq j \leq k $), | ||
| + | are arbitrary complex numbers, and $ \sigma _ {k} - 1 < \beta < \sigma _ {k} < \dots < \sigma _ {1} $, | ||
| + | then the Dirichlet series converges for $ \sigma > \sigma _ {1} $, | ||
| + | and $ \phi (s) $ | ||
| + | is regular in the domain $ \sigma > \beta $ | ||
| + | with the exception of the points $ s _ {1} \dots s _ {k} $ | ||
| + | at which it has algebraic or logarithmic singularities. Theorems of this type yield information on the behaviour of the Dirichlet series in a given half-plane, based on the asymptotic behaviour of $ A _ {n} $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> N.H. Abel, , ''Oeuvres complètes, nouvelle éd.'' , '''1''' , Grondahl & Son , Christiania (1881) (Edition de Holmboe)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> N.H. Abel, "Untersuchungen über die Reihe <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010180/a01018065.png" />" ''J. Reine Angew. Math.'' , '''1''' (1826) pp. 311–339 {{MR|}} {{ZBL|26.0277.02}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A.I. Markushevich, "Theory of functions of a complex variable" , '''1''' , Chelsea (1977) (Translated from Russian) {{MR|0444912}} {{ZBL|0357.30002}} </TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> N.H. Abel, , ''Oeuvres complètes, nouvelle éd.'' , '''1''' , Grondahl & Son , Christiania (1881) (Edition de Holmboe)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> N.H. Abel, "Untersuchungen über die Reihe <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010180/a01018065.png" />" ''J. Reine Angew. Math.'' , '''1''' (1826) pp. 311–339 {{MR|}} {{ZBL|26.0277.02}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A.I. Markushevich, "Theory of functions of a complex variable" , '''1''' , Chelsea (1977) (Translated from Russian) {{MR|0444912}} {{ZBL|0357.30002}} </TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
Revision as of 13:00, 8 February 2020
Abel's theorem on algebraic equations: Formulas expressing the solution of an arbitrary equation of degree $ n $
in terms of its coefficients using radicals do not exist for any $ n \geq 5 $.
The theorem was proved by N.H. Abel in 1824 . Abel's theorem may also be obtained as a corollary of Galois theory, from which a more general theorem follows: For any $ n \geq 5 $
there exist algebraic equations with integer coefficients whose roots cannot be expressed in terms of radicals of rational numbers. For a modern formulation of Abel's theorem for equations over an arbitrary field, see Algebraic equation.
Abel's theorem on power series: If the power series
$$ \tag{*} S ( z ) \ = \ \sum _ {k = 0} ^ \infty a _ {k} ( z - b ) ^ {k} , $$
where $ a _ {k} ,\ b,\ z $ are complex numbers, converges at $ z = z _ {0} $, then it converges absolutely and uniformly within any disc $ | z - b | \leq \rho $ of radius $ \rho < | z _ {0} - b | $ and with centre at $ b $. The theorem was established by N.H. Abel . It follows from the theorem that there exists a number $ R \in [ 0,\ \infty ] $ such that if $ | z - b | < R $ the series is convergent, while if $ | z - b | > R $ the series is divergent. The number $ R $ is called the radius of convergence of the series (*), while the disc $ | z - b | < R $ is known as the disc of convergence of the series (*).
Abel's continuity theorem: If the power series
converges at a point $ z _ {0} $ on the boundary of the disc of convergence, then it is a continuous function in any closed triangle $ T $ with vertices $ z _ {0} ,\ z _ {1} ,\ z _ {2} $, where $ z _ {1} ,\ z _ {2} $ are located inside the disc of convergence. In particular
$$ \lim\limits _ {\begin{array}{c} z \rightarrow z _ {0} , \\ z \in T \end{array} } \ S ( z ) \ = \ S ( z _ {0} ) . $$
This limit always exists along the radius: The series
converges uniformly along any radius of the disc of convergence joining the points $ b $ and $ z _ {0} $. This theorem is used, in particular, to calculate the sum of a power series which converges at the boundary points of the disc of convergence.
Abel's theorem on Dirichlet series: If the Dirichlet series
$$ \phi ( s ) \ = \ \sum _ {n = 1} ^ \infty a _ {n} e ^ {- \lambda _ {n} s} , \ \ s = \sigma + it ,\ \ \lambda _ {n} > 0 , $$
converges at the point $ s _ {0} = \sigma _ {0} + i t _ {0} $, then it converges in the half-plane $ \sigma > \sigma _ {0} $ and converges uniformly inside any angle $ | \mathop{\rm arg} (s - s _ {0} ) | \leq \theta < \pi / 2 $. It is a generalization of Abel's theorem on power series (take $ \lambda _ {n} = n $ and put $ e ^ {-s} = z $). It follows from the theorem that the domain of convergence of a Dirichlet series is some half-plane $ \sigma > c $, where $ c $ is the abscissa of convergence of the series.
The following theorem is valid for an ordinary Dirichlet series (when $ \lambda _ {n} = \mathop{\rm ln} \ n $) with a known asymptotic behaviour for the sum-function $ A _ {n} = a _ {1} + \dots + a _ {n} $ of the coefficients of the series: If
$$ A _ {n} \ = \ B \ n ^ {s _ 1} ( \mathop{\rm ln} \ n ) ^ \alpha + O ( n ^ \beta ) , $$
where $ B ,\ s _ {1} ,\ \alpha $ are complex numbers, $ \beta $ is a real number, $ \sigma _ {1} - 1 < \beta < \sigma _ {1} $, $ \sigma _ {1} = \mathop{\rm Re} \ s _ {1} $, then the Dirichlet series converges for $ \sigma _ {1} < \sigma $, and the function $ \phi (s) $ can be regularly extended to the half-plane $ \beta < \sigma $ with the exception of the point $ s = s _ {1} $. Moreover
$$ \phi ( s ) \ = \ B \ \Gamma ( \alpha + 1 ) s ( s - s _ {1} ) ^ {- \alpha - 1} + g ( s ) $$
if $ \alpha \neq -1,\ -2 \dots $ and
$$ \phi ( s ) \ = \ B \frac{( - 1 ) ^ {- \alpha}}{( - \alpha - 1 ) !} s ( s - s _ {1} ) ^ {- \alpha - 1} \ \mathop{\rm ln} ( s - s _ {1} ) + g ( s ) $$
if $ \alpha = -1,\ -2 ,\dots $. Here $ g(s) $ is a regular function for $ \sigma > \beta $.
E.g., the Riemann zeta-function $ \zeta (s) $( $ A _ {n} = n $, $ B = 1 $, $ s _ {1} = 1 $, $ \alpha = 0 $, $ \beta > 0 $) is regular at least in the half-plane $ \sigma > 0 $, with the exception of the point $ s = 1 $ at which it has a first-order pole with residue $ 1 $. This theorem can be generalized in various ways. E.g., if
$$ A _ {n} \ = \ \sum _ {j = 1} ^ { k } B _ {j} n ^ {s _ j} ( \mathop{\rm ln} \ n ) ^ {\alpha _ j} + O ( n ^ \beta ) , $$
where $ B _ {j} ,\ s _ {j} ,\ \alpha _ {j} $( $ 1 \leq j \leq k $), are arbitrary complex numbers, and $ \sigma _ {k} - 1 < \beta < \sigma _ {k} < \dots < \sigma _ {1} $, then the Dirichlet series converges for $ \sigma > \sigma _ {1} $, and $ \phi (s) $ is regular in the domain $ \sigma > \beta $ with the exception of the points $ s _ {1} \dots s _ {k} $ at which it has algebraic or logarithmic singularities. Theorems of this type yield information on the behaviour of the Dirichlet series in a given half-plane, based on the asymptotic behaviour of $ A _ {n} $.
References
| [1] | N.H. Abel, , Oeuvres complètes, nouvelle éd. , 1 , Grondahl & Son , Christiania (1881) (Edition de Holmboe) |
| [2] | N.H. Abel, "Untersuchungen über die Reihe 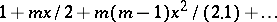 " J. Reine Angew. Math. , 1 (1826) pp. 311–339 Zbl 26.0277.02 " J. Reine Angew. Math. , 1 (1826) pp. 311–339 Zbl 26.0277.02 |
| [3] | A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) (Translated from Russian) MR0444912 Zbl 0357.30002 |
Comments
More on Abel's theorems 2)–4) can be found in [a1].
References
| [a1] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) MR0030620 Zbl 0032.05801 |
Abel theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Abel_theorem&oldid=44392