User:Ulf Rehmann/Table of automatically generated TeX code

Nr.	Image of png File	$\TeX$, 1st version	$\TeX$, 2nd version	Confidence, F? name of png
Algebraic curve
1.(23.)		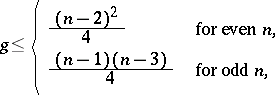$g \leq \left\{ \begin{array} { l l } { \frac { ( n - 2 ) ^ { 2 } } { 4 } } & { \text { for even } n } \\ { \frac { ( n - 1 ) ( n - 3 ) } { 4 } } & { \text { for odd } n } \end{array} \right.$	$$ g \leq \left\{ \begin{array} { l l } { \frac { ( n - 2 ) ^ { 2 } } { 4 } } & { \text { for even } n, } \\ { \frac { ( n - 1 ) ( n - 3 ) } { 4 } } & { \text { for odd } n, } \end{array} \right.$$	conf 0.698 png = a01145065.png(65)
Algebraic geometry
2.(116.)		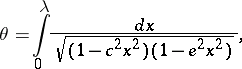$\theta = \int _ { 0 } ^ { \lambda } \frac { d x } { \sqrt { ( 1 - c ^ { 2 } x ^ { 2 } ) ( 1 - e ^ { 2 } x ^ { 2 } ) } }$	$$\empty$$	conf 0.997 png = a01150014.png(14)
3.(133.)		$\omega = 2 \int _ { 0 } ^ { 1 / c } \frac { d x } { \sqrt { ( 1 - c ^ { 2 } x ^ { 2 } ) ( 1 - e ^ { 2 } x ^ { 2 } ) } }$	$$\empty$$	conf 0.973 png = a01150021.png(21)
4.(67.)		$\overline { w } = 2 \int _ { 0 } ^ { 1 / \varepsilon } \frac { d x } { \sqrt { ( 1 - c ^ { 2 } x ^ { 2 } ) ( 1 - e ^ { 2 } x ^ { 2 } ) } }$	$$\widetilde{ w } = 2 \int _ { 0 } ^ { 1 / \varepsilon } \frac { d x } { \sqrt { ( 1 - c ^ { 2 } x ^ { 2 } ) ( 1 - e ^ { 2 } x ^ { 2 } ) } },$$	conf 0.107 png = a01150022.png(22)
5.(105.)		$\theta ( v + \pi i r ) = \theta ( r ) , \quad \theta ( v + \alpha _ { j } ) = e ^ { L _ { j } ( v ) } \theta ( v )$	$$\empty$$	conf 0.775 png = a01150044.png(44)
6.(17.)		$\left( \begin{array} { l l } { \alpha } & { b } \\ { c } & { d } \end{array} \right) \equiv \left( \begin{array} { l l } { 1 } & { 0 } \\ { 0 } & { 1 } \end{array} \right) ( \operatorname { mod } 7 )$	$$\empty$$	conf 0.440 png = a01150078.png(78)
Algebraic surface
7.(144.)		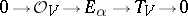$0 \rightarrow O _ { V } \rightarrow E _ { \alpha } \rightarrow T _ { V } \rightarrow 0$	$$0 \rightarrow {\cal O} _ { V } \rightarrow E _ { \alpha } \rightarrow T _ { V } \rightarrow 0$$	conf 0.981 png = a011640132.png(132)
8.(73.)		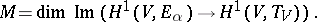$M = \operatorname { dim } \operatorname { Im } ( H ^ { 1 } ( V , E _ { \alpha } ) \rightarrow H ^ { 1 } ( V , T _ { V } ) )$	$$\empty$$	conf 0.997 png = a011640137.png(137)
9.(88.)		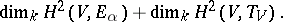$\operatorname { dim } _ { k } H ^ { 2 } ( V , E _ { \alpha } ) + \operatorname { dim } _ { k } H ^ { 2 } ( V , T _ { V } )$	$$\empty$$	conf 0.996 png = a011640139.png(139)
10.(117.)		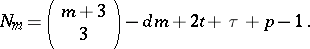$N _ { m } = \left( \begin{array} { c } { m + 3 } \\ { 3 } \end{array} \right) - d m + 2 t + \tau + p - 1$	$$\empty$$	conf 0.369 png = a01164027.png(27)
11.(72.)		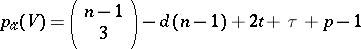$p _ { \alpha } ( V ) = \left( \begin{array} { c } { n - 1 } \\ { 3 } \end{array} \right) - d ( n - 1 ) + 2 t + \tau + p - 1$	$$\empty$$	conf 0.396 png = a01164029.png(29)
12.(68.)*		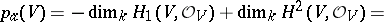$p _ { x } ( V ) = - \operatorname { dim } _ { k } H _ { 1 } ( V , O _ { V } ) + \operatorname { dim } _ { k } H ^ { 2 } ( V , O _ { V } ) =$	$$p _ { \alpha } ( V ) = - \operatorname { dim } _ { k } H _ { 1 } ( V , {\cal O} _ { V } ) + \operatorname { dim } _ { k } H ^ { 2 } ( V , {\cal O} _ { V } ) =$$	conf 0.756 F png = a01164047.png(47)
13.(93.)*		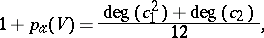$1 + p _ { x } ( V ) = \frac { \operatorname { deg } ( c _ { 1 } ^ { 2 } ) + \operatorname { deg } ( c _ { 2 } ) } { 12 }$	$$ 1 + p _ { \alpha } ( V ) = \frac { \operatorname { deg } ( c _ { 1 } ^ { 2 } ) + \operatorname { deg } ( c _ { 2 } ) } { 12 },$$	conf 0.752 F png = a01164053.png(53)
Cartan subalgebra
14.(33.)*		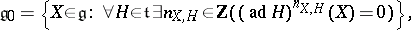$\mathfrak { g } 0 = \{ X \in \mathfrak { g } : \forall H \in \mathfrak { t } \exists \mathfrak { n } X , H \in Z ( ( \text { ad } H ) ^ { n } X , H ( X ) = 0 ) \}$	$$\mathfrak { g }_0 = \big\{ X \in \mathfrak { g } : \forall H \in \mathfrak { t } \exists { n }_{X,H} \in {\mathbb Z} ( ( \text { ad } H ) ^ { n_{X , H} } ( X ) = 0 ) \big\}$$	conf 0.110 F png = c0205509.png(9)
Cartan theorem
15.(49.)*		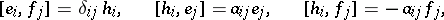$f _ { j } ] = \delta _ { i j } h _ { i } , \quad [ h _ { i } , e _ { j } ] = \alpha _ { i j } e _ { j } , \quad [ h _ { i } , f _ { j } ] = - \alpha _ { j } f _ { j }$	$$\empty$$	conf 0.149 F png = c0205704.png(4)
16.(55.)*		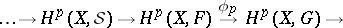$\rightarrow H ^ { p } ( X , S ) \rightarrow H ^ { p } ( X , F ) \stackrel { \phi p } { \rightarrow } H ^ { p } ( X , G ) \rightarrow$	$$\empty$$	conf 0.853 F png = c02057064.png(64)
Comitant
17.(7.)		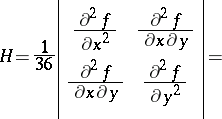$H = \frac { 1 } { 36 } \left| \begin{array} { c c } { \frac { \partial ^ { 2 } f } { \partial x ^ { 2 } } } & { \frac { \partial ^ { 2 } f } { \partial x \partial y } } \\ { \frac { \partial ^ { 2 } f } { \partial x \partial y } } & { \frac { \partial ^ { 2 } f } { \partial y ^ { 2 } } } \end{array} \right| =$	$$\empty$$	conf 0.956 png = c02333033.png(33)
18.(76.)		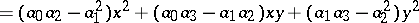$= ( a _ { 0 } a _ { 2 } - a _ { 1 } ^ { 2 } ) x ^ { 2 } + ( a _ { 0 } a _ { 3 } - a _ { 1 } a _ { 2 } ) x y + ( a _ { 1 } a _ { 3 } - a _ { 2 } ^ { 2 } ) y ^ { 2 }$	$$\empty$$	conf 0.549 png = c02333034.png(34)
19.(11.)*		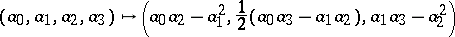$( \alpha _ { 0 } , \alpha _ { 1 } , \alpha _ { 2 } , \alpha _ { 3 } ) \mapsto ( \alpha _ { 0 } \alpha _ { 2 } - \alpha _ { 1 } ^ { 2 } , \frac { 1 } { 2 } ( \alpha _ { 0 } \alpha _ { 3 } - \alpha _ { 1 } \alpha _ { 2 } ) , \alpha _ { 1 } \alpha _ { 3 } - \alpha _ { 2 } ^ { 2 } )$	$$\empty$$	conf 0.521 F png = c02333035.png(35)
Deformation
20.(26.)		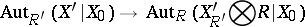$\operatorname { Aut } _ { R ^ { \prime } } ( X ^ { \prime } | X _ { 0 } ) \rightarrow \operatorname { Aut } _ { R } ( X _ { R ^ { \prime } } ^ { \prime } \otimes R | X _ { 0 } )$	$$\empty$$	conf 0.683 png = d030700175.png(175)
21.(27.)		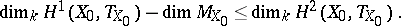$\operatorname { dim } _ { k } H ^ { 1 } ( X _ { 0 } , T _ { X _ { 0 } } ) - \operatorname { dim } M _ { X _ { 0 } } \leq \operatorname { dim } _ { k } H ^ { 2 } ( X _ { 0 } , T _ { X _ { 0 } } )$	$$\empty$$	conf 0.944 png = d030700190.png(190)
22.(78.)*		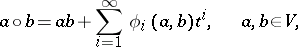$\alpha \circ b = \alpha b + \sum _ { i = 1 } ^ { \infty } \phi _ { i } ( \alpha , b ) t ^ { i } , \quad \alpha , b \in V$	$$\empty$$	conf 0.097 F png = d030700263.png(263)
23.(96.)*		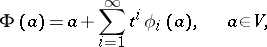$\Phi ( \alpha ) = \alpha + \sum _ { i = 1 } ^ { \infty } t ^ { i } \phi _ { i } ( \alpha ) , \quad \alpha \in V$	$$\empty$$	conf 0.873 F png = d030700270.png(270)
Differential algebra
24.(106.)		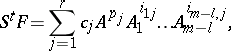$S ^ { t } F = \sum _ { j = 1 } ^ { r } c _ { j } A ^ { p _ { j } } A _ { 1 } ^ { i _ { 1 j } } \dots A _ { m - l } ^ { i _ { m - l } , j }$	$$\empty$$	conf 0.149 png = d031830107.png(107)
25.(146.)*		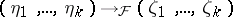$( \eta _ { 1 } , \ldots , \eta _ { k } ) \rightarrow F ( \zeta _ { 1 } , \ldots , \zeta _ { k } )$	$$\empty$$	conf 0.562 F png = d031830141.png(141)
26.(145.)$^F$*		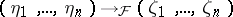$( \eta _ { 1 } , \ldots , \eta _ { n } ) \rightarrow F ( \zeta _ { 1 } , \ldots , \zeta _ { n } )$	$$\empty$$	conf 0.376 F png = d031830150.png(150)
27.(57.)		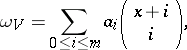$\omega _ { V } = \sum _ { 0 \leq i \leq m } \alpha _ { i } \left( \begin{array} { c } { x + i } \\ { i } \end{array} \right)$	$$\empty$$	conf 0.780 png = d03183016.png(16)
28.(111.)		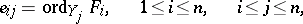$e _ { i j } = \operatorname { ord } _ { Y } _ { j } F _ { i } , \quad 1 \leq i \leq n , \quad i \leq j \leq n$	$$ e_ { i j } = \operatorname { ord } _ { { Y } _ { j } } F _ { i } , \quad 1 \leq i \leq n , \quad i \leq j \leq n$$	conf 0.187 png = d03183043.png(43)
Dimension polynomial
29.(48.)		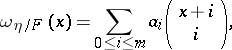$\omega _ { \eta / F } ( x ) = \sum _ { 0 \leq i \leq m } \alpha _ { i } \left( \begin{array} { c } { x + i } \\ { i } \end{array} \right)$	$$\empty$$	conf 0.968 png = d03249029.png(29)
Duality
30.(118.)*		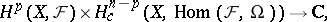$H ^ { p } ( X , F ) \times H _ { c } ^ { n - p } ( X , \operatorname { Hom } ( F , \Omega ) ) \rightarrow C$	$$\empty$$	conf 0.824 F png = d034120173.png(173)
31.(59.)*		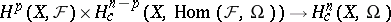$H ^ { p } ( X , F ) \times H _ { c } ^ { n - p } ( X , \operatorname { Hom } ( F , \Omega ) ) \rightarrow H _ { c } ^ { n } ( X , \Omega )$	$$\empty$$	conf 0.921 F png = d034120175.png(175)
32.(124.)*		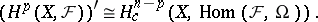$( H ^ { p } ( X , F ) ) ^ { \prime } \cong H _ { c } ^ { n - p } ( X , \operatorname { Hom } ( F , \Omega ) )$	$$\empty$$	conf 0.829 F png = d034120184.png(184)
33.(29.)*		$\beta : \operatorname { Ext } _ { c } ^ { n - p - 1 } ( X F , \Omega ) \rightarrow \operatorname { Ext } _ { c } ^ { n - p - 1 } ( X \backslash Y || F , \Omega )$	$$\empty$$	conf 0.634	F png = d034120236.png(236)
34.(77.)*		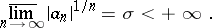$\underset { n \rightarrow \infty } { \operatorname { lim } } | \alpha _ { n } | ^ { 1 / n } = \sigma < + \infty$	$$\empty$$	conf 0.521 F png = d034120247.png(247)
35.(58.)*		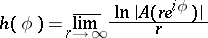$h ( \phi ) = \operatorname { lim } _ { r \rightarrow \infty } \frac { \operatorname { ln } | A ( r e ^ { i \phi } ) | } { r }$	$$\empty$$	conf 0.861 F png = d034120253.png(253)
36.(69.)*		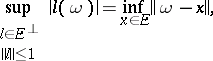$\operatorname { sup } _ { l \in E ^ { \perp } } | l ( \omega ) | = \operatorname { inf } _ { x \in E } \| \omega - x \|$	$$\empty$$	conf 0.293 F png = d034120360.png(360)
37.(15.)		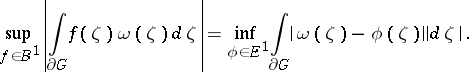$\operatorname { sup } _ { f \in B ^ { 1 } } | \int _ { \partial G } f ( \zeta ) \omega ( \zeta ) d \zeta | = \operatorname { inf } _ { \phi \in E ^ { 1 } } \int _ { \partial G } | \omega ( \zeta ) - \phi ( \zeta ) \| d \zeta |$	$$\empty$$	conf 0.508 png = d034120376.png(376)
38.(52.)		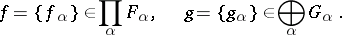$f = \{ f _ { \alpha } \} \in \prod _ { \alpha } F _ { \alpha } , \quad g = \{ g _ { \alpha } \} \in \oplus _ { \alpha } G _ { \alpha }$	$$\empty$$	conf 0.491 png = d034120509.png(509)
39.(140.)		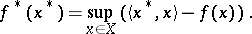$f ^ { * } ( x ^ { * } ) = \operatorname { sup } _ { x \in X } ( \langle x ^ { * } , x \rangle - f ( x ) )$	$$\empty$$	conf 0.900 png = d034120535.png(535)
40.(94.)		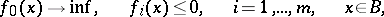$f _ { 0 } ( x ) \rightarrow \text { inf, } \quad f _ { i } ( x ) \leq 0 , \quad i = 1 , \ldots , m , \quad x \in B$	$$\empty$$	conf 0.810 png = d034120555.png(555)
41.(74.)*		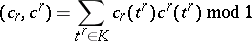$( c _ { \gamma } , c ^ { r } ) = \sum _ { t ^ { r } \in K } c _ { r } ( t ^ { \prime } ) c ^ { r } ( t ^ { r } ) \operatorname { mod } 1$	$$\empty$$	conf 0.117 F png = d03412079.png(79)
Extension of a differential field
42.(63.)		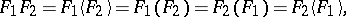$F _ { 1 } F _ { 2 } = F _ { 1 } \langle F _ { 2 } \rangle = F _ { 1 } ( F _ { 2 } ) = F _ { 2 } ( F _ { 1 } ) = F _ { 2 } \langle F _ { 1 } \rangle$	$$\empty$$	conf 0.628 png = e03696024.png(24)
Formal group
43.(120.)*		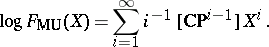$\operatorname { og } F _ { MU } ( X ) = \sum _ { i = 1 } ^ { \infty } i ^ { - 1 } [ C ^ { - } P ^ { - 1 } ] X ^ { i }$	$$\empty$$	conf 0.098 F png = f040820118.png(118)
44.(147.)*		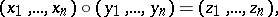$( x _ { 1 } , \ldots , x _ { x } ) \circ ( y _ { 1 } , \ldots , y _ { n } ) = ( z _ { 1 } , \ldots , z _ { x } )$	$$\empty$$	conf 0.553 F png = f04082059.png(59)
Gel'fond-Schneider method
45.(148.)		$\alpha ^ { \beta } = \operatorname { exp } \{ \beta \operatorname { log } \alpha \}$	$$\empty$$	conf 0.979 png = g1300205.png(5)
Group
46.(22.)*		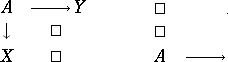$\left. \begin{array} { l l l } { A } & { \rightarrow Y } & { \square } \\ { \downarrow } & { \square } & { } & { \square } \\ { X } & { \square } & { } & { A } \end{array} \right.$	$$\empty$$	conf 0.226 F png = g04521075.png(75)
Homogeneous space
47.(89.)		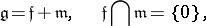$\mathfrak { g } = \mathfrak { f } + \mathfrak { m } , \quad \mathfrak { f } \cap \mathfrak { m } = \{ 0 \}$	$$\empty$$	conf 0.793 png = h04769069.png(69)
Hopf algebra
48.(103.)		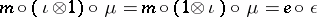$m \circ ( \iota \otimes 1 ) \circ \mu = m \circ ( 1 \otimes \iota ) \circ \mu = e \circ \epsilon$	$$\empty$$	conf 0.618 png = h047970129.png(129)
49.(107.)*		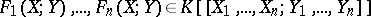$F _ { 1 } ( X || Y ) , \ldots , F _ { n } ( X || Y ) \in K [ X _ { 1 } , \ldots , X _ { n } || Y _ { 1 } , \ldots , Y _ { n } ] \}$	$$\empty$$	conf 0.353 F png = h047970139.png(139)
50.(97.)		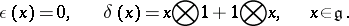$\epsilon ( x ) = 0 , \quad \delta ( x ) = x \bigotimes 1 + 1 \bigotimes x , \quad x \in \mathfrak { g }$	$$\empty$$	conf 0.213 png = h04797042.png(42)
Invariants, theory of
51.(149.)*		$\alpha _ { 1 } , \ldots , i _ { R } \rightarrow \alpha _ { 2 } ^ { \prime } , \ldots , i _ { R }$	$$\empty$$	conf 0.142 F png = i05235015.png(15)
Jordan algebra
52.(150.)		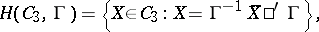$H ( C _ { 3 } , \Gamma ) = \{ X \in C _ { 3 } : X = \Gamma ^ { - 1 } X \square ^ { \prime } \Gamma \}$	$$\empty$$	conf 0.651 png = j05427030.png(30)
53.(42.)		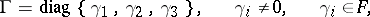$\Gamma = \operatorname { diag } \{ \gamma _ { 1 } , \gamma _ { 2 } , \gamma _ { 3 } \} , \quad \gamma _ { i } \neq 0 , \quad \gamma _ { i } \in F$	$$\empty$$	conf 0.987 png = j05427031.png(31)
54.(125.)*		$\mathfrak { g } = \mathfrak { g } - 1 + \mathfrak { g } \mathfrak { d } + \mathfrak { g } _ { 1 }$	$$\empty$$	conf 0.598 F png = j05427077.png(77)
Jordan matrix
55.(6.)*		$J = \left| \begin{array} { c c c c } { J _ { n _ { 1 } } ( \lambda _ { 1 } ) } & { \square } & { \square } & { \square } \\ { \square } & { \ldots } & { \square } & { 0 } \\ { 0 } & { \square } & { \ldots } & { \square } \\ { \square } & { \square } & { \square } & { J _ { n _ { S } } ( \lambda _ { s } ) } \end{array} \right|$	$$J = \left\| \begin{array} { c c c c } J_{n_1}(\lambda_1) & 0 & 0 & 0 \\ 0 & \ddots & \ddots & 0 \\ 0 & \ddots & \ddots & 0 \\ 0 & 0 & 0 & J_{n_s}(\lambda_s) \end{array} \right\|,$$	conf 0.072 F png = j0543403.png(3)
56.(64.)		$C _ { m } ( \lambda ) = \operatorname { rk } ( A - \lambda E ) ^ { m - 1 } - 2 \operatorname { rk } ( A - \lambda E ) ^ { m } +$	$$\empty$$	conf 0.955 png = j05434030.png(30)
57.(1.)*		$J _ { m } ( \lambda ) = \| \begin{array} { c c c c c c } { \lambda } & { 1 } & { \square } & { \square } & { \square } & { \square } \\ { \square } & { \lambda } & { 1 } & { \square } & { 0 } & { \square } \\ { \square } & { \square } & { \cdots } & { \square } & { \square } & { \square } \\ { \square } & { \square } & { \square } & { \cdots } & { \square } & { \square } \\ { \square } & { 0 } & { \square } & { \square } & { \lambda } & { 1 } \\ { \square } & { \square } & { \square } & { \square } & { \square } & { \lambda } \end{array} ]$	$$J_m(\lambda) = \left\| \begin{array} { c c c c c c } \lambda & 1 & \square & \square & \square & \square \\ \square & \lambda & 1 & \square & 0 & \square \\ \square & \square & \ddots & \ddots & \square & \square\\ \square & \square & \square & \ddots & \ddots & \square \\ \square & 0 & \square & \square & \lambda & 1 \\ \square & \square & \square & \square & \square & \lambda \end{array} \right\|,$$	conf 0.098 F png = j0543406.png(6)
Lie algebra, semi-simple
58.(5.)		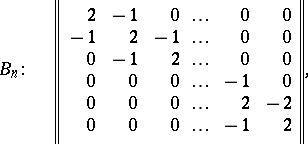$\left\| \begin{array} { r r r r r r } { 2 } & { - 1 } & { 0 } & { \dots } & { 0 } & { 0 } \\ { - 1 } & { 2 } & { - 1 } & { \dots } & { 0 } & { 0 } \\ { 0 } & { - 1 } & { 2 } & { \dots } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { - 1 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { 2 } & { - 2 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { - 1 } & { 2 } \end{array} \right\|$	$$B_n: \quad \left\| \begin{array} { r r r r r r } { 2 } & { - 1 } & { 0 } & { \dots } & { 0 } & { 0 } \\ { - 1 } & { 2 } & { - 1 } & { \dots } & { 0 } & { 0 } \\ { 0 } & { - 1 } & { 2 } & { \dots } & { 0 } & { 0 } \\ \cdot & \cdot & \cdot & \dots & \cdot & \cdot \\ { 0 } & { 0 } & { 0 } & { \dots } & { - 1 } & { 0 }\\ { 0 } & { 0 } & { 0 } & { \dots } & { 2 } & { - 2 }\\ { 0 } & { 0 } & { 0 } & { \dots } & { - 1 } & { 2 } \end{array} \right\|,$$	conf 0.232 png = l058510127.png(127)
59.(3.)*		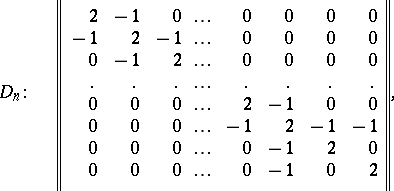$\| \left. \begin{array} { r r r r r r r } { 2 } & { - 1 } & { 0 } & { \dots } & { 0 } & { 0 } & { 0 } & { 0 } \\ { - 1 } & { 2 } & { - 1 } & { \dots } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { - 1 } & { 2 } & { \dots } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { 2 } & { - 1 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { - 1 } & { 2 } & { - 1 } & { - 1 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { 0 } & { - 1 } & { 2 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { 0 } & { - 1 } & { 0 } & { 2 } \end{array} \right. |$	$$D_n: \quad \left\| \begin{array} { r r r r r r r } { 2 } & { - 1 } & { 0 } & { \dots } & { 0 } & { 0 } & { 0 } & { 0 } \\ { - 1 } & { 2 } & { - 1 } & { \dots } & { 0 } & { 0 } & { 0 } & { 0 }\\ { 0 } & { - 1 } & { 2 } & { \dots } & { 0 } & { 0 } & { 0 } & { 0 } \\ \cdot & \cdot & \cdot & \dots & \cdot & \cdot &\cdot & \cdot \\ { 0 } & { 0 } & { 0 } & { \dots } & { 2 } & { - 1 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { - 1 } & { 2 } & { - 1 } & { - 1 }\\ { 0 } & { 0 } & { 0 } & { \dots } & { 0 } & { - 1 } & { 2 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { 0 } & { - 1 } & { 0 } & { 2 } \end{array} \right\|,$$	conf 0.055 F png = l058510129.png(129)
60.(8.)*		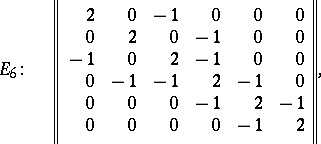$\left\| \begin{array} { r r r r r r } { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } \\ { - 1 } & { 0 } & { 2 } & { - 1 } & { 0 } & { 0 } \\ { 0 } & { - 1 } & { - 1 } & { 2 } & { - 1 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } \end{array} \right\|$	$$E_6: \quad \left\| \begin{array} { r r r r r r } { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } \\ { - 1 } & { 0 } & { 2 } & { - 1 } & { 0 } & { 0 } \\ { 0 } & { - 1 } & { - 1 } & { 2 } & { - 1 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } \end{array} \right\|,$$	conf 0.628 F png = l058510130.png(130)
61.(4.)		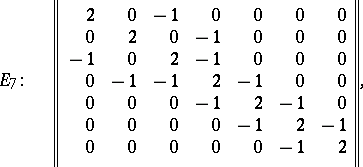$\left\| \begin{array} { r r r r r r r } { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } & { 0 } \\ { 1 } & { 0 } & { 2 } & { - 1 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { - 1 } & { - 1 } & { 2 } & { - 1 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } \end{array} \right\|$	$$E_7: \quad \left\| \begin{array} { r r r r r r r } { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } & { 0 } \\ {-1 } & { 0 } & { 2 } & { - 1 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { - 1 } & { - 1 } & { 2 } & { - 1 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } \end{array} \right\|,$$	conf 0.278 png = l058510131.png(131)
62.(2.)*		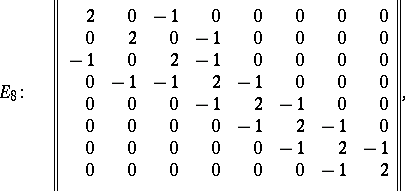$\left. \begin{array} { r l l l l l l l } { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 1 } & { 0 } & { 2 } & { - 1 } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { - 1 } & { - 1 } & { 2 } & { - 1 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } \end{array} \right.$	$$E_8: \quad \left\| \begin{array} { r r r r r r r r } { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } & { 0 } & { 0 } \\ {-1 } & { 0 } & { 2 } & { - 1 } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { - 1 } & { - 1 } & { 2 } & { - 1 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } \end{array} \right\|,$$	conf 0.354 F png = l058510132.png(132)
63.(10.)*		$\left\| \begin{array} { r r r r } { 2 } & { - 1 } & { 0 } & { 0 } \\ { - 1 } & { 2 } & { - 2 } & { 0 } \\ { 0 } & { - 1 } & { 2 } & { - 1 } \\ { 0 } & { 0 } & { - 1 } & { 2 } \end{array} \right\| , \quad G _ { 2 } : \quad \left\| \begin{array} { r r } { 2 } & { - 1 } \\ { - 3 } & { 2 } \end{array} \right\|$	$$F_4: \quad \left\| \begin{array} { r r r r } { 2 } & { - 1 } & { 0 } & { 0 } \\ { - 1 } & { 2 } & { - 2 } & { 0 } \\ { 0 } & { - 1 } & { 2 } & { - 1 } \\ { 0 } & { 0 } & { - 1 } & { 2 } \end{array} \right\| , \quad G _ { 2 } : \quad \left\| \begin{array} { r r } { 2 } & { - 1 } \\ { - 3 } & { 2 } \end{array} \right\|.$$	conf 0.374 F png = l058510133.png(133)
64.(98.)		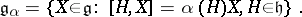$\mathfrak { g } _ { \alpha } = \{ X \in \mathfrak { g } : [ H , X ] = \alpha ( H ) X , H \in \mathfrak { h } \}$	$$\empty$$	conf 0.976 png = l05851030.png(30)
65.(126.)		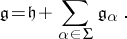$\mathfrak { g } = \mathfrak { h } + \sum _ { \alpha \in \Sigma } \mathfrak { g } _ { \alpha }$	$$\empty$$	conf 0.945 png = l05851037.png(37)
66.(61.)*		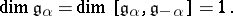$\mathfrak { g } _ { \alpha } = \operatorname { dim } [ \mathfrak { g } _ { \alpha } , \mathfrak { g } _ { - \alpha } ] = 1$	$$\empty$$	conf 0.520 F png = l05851044.png(44)
67.(65.)*		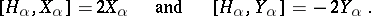$[ H _ { \alpha } , X _ { \alpha } ] = 2 X _ { \alpha } \quad \text { and } \quad [ H _ { \alpha } , Y _ { \alpha } ] = - 2 Y _ { 0 }$	$$\empty$$	conf 0.539 F png = l05851050.png(50)
68.(70.)		$\beta ( H _ { \alpha } ) = \frac { 2 ( \alpha , \beta ) } { ( \alpha , \alpha ) } , \quad \alpha , \beta \in \Sigma$	$$\empty$$	conf 0.997 png = l05851051.png(51)
69.(112.)		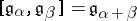$[ \mathfrak { g } _ { \alpha } , \mathfrak { g } _ { \beta } ] = \mathfrak { g } _ { \alpha + \beta }$	$$\empty$$	conf 0.917 png = l05851057.png(57)
70.(127.)		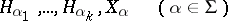$H _ { \alpha _ { 1 } } , \ldots , H _ { \alpha _ { k } } , X _ { \alpha } \quad ( \alpha \in \Sigma )$	$$\empty$$	conf 0.432 png = l05851064.png(64)
71.(113.)*		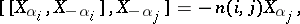$[ [ X _ { \alpha _ { i } } , X _ { - } \alpha _ { i } ] , X _ { - \alpha _ { j } } ] = - n ( i , j ) X _ { \alpha _ { j } }$	$$\empty$$	conf 0.628 F png = l05851069.png(69)
72.(79.)		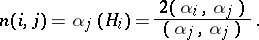$n ( i , j ) = \alpha _ { j } ( H _ { i } ) = \frac { 2 ( \alpha _ { i } , \alpha _ { j } ) } { ( \alpha _ { j } , \alpha _ { j } ) }$	$$\empty$$	conf 0.992 png = l05851073.png(73)
73.(13.)		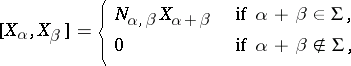$[ X _ { \alpha } , X _ { \beta } ] = \left\{ \begin{array} { l l } { N _ { \alpha , \beta } X _ { \alpha + \beta } } & { \text { if } \alpha + \beta \in \Sigma } \\ { 0 } & { \text { if } \alpha + \beta \notin \Sigma } \end{array} \right.$	$$\empty$$	conf 0.988 png = l05851074.png(74)
74.(80.)		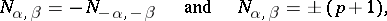$N _ { \alpha , \beta } = - N _ { - \alpha , - \beta } \quad \text { and } \quad N _ { \alpha , \beta } = \pm ( p + 1 )$	$$\empty$$	conf 0.961 png = l05851078.png(78)
75.(85.)*		$X _ { \alpha } - X _ { - \alpha } , \quad i ( X _ { \alpha } + X _ { - \alpha } ) \quad ( \alpha \in \Sigma _ { + } )$	$$\empty$$	conf 0.691 F png = l05851085.png(85)
Lie algebra, solvable
76.(119.)*		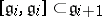$[ \mathfrak { g } _ { i } , \mathfrak { g } _ { i } ] \subset \mathfrak { g } _ { \mathfrak { i } } + 1$	$$\empty$$	conf 0.276 F png = l05852011.png(11)
77.(141.)		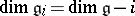$\operatorname { dim } \mathfrak { g } _ { i } = \operatorname { dim } \mathfrak { g } - i$	$$\empty$$	conf 0.901 png = l05852046.png(46)
Lie group
78.(62.)*		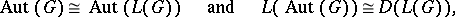$( G ) \cong \operatorname { Aut } ( L ( G ) ) \quad \text { and } \quad L ( \operatorname { Aut } ( G ) ) \cong D ( L ( G ) )$	$$\empty$$	conf 0.693 F png = l058590115.png(115)
79.(50.)		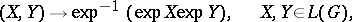$( X , Y ) \rightarrow \operatorname { exp } ^ { - 1 } ( \operatorname { exp } X \operatorname { exp } Y ) , \quad X , Y \in L ( G )$	$$\empty$$	conf 0.856 png = l05859086.png(86)
Lie group, compact
80.(121.)*		$J = \left\| \begin{array} { c c } { 0 } & { E _ { x } } \\ { - E _ { x } } & { 0 } \end{array} \right\|$	$$\empty$$	conf 0.364 F png = l05861012.png(12)
Lie group, nilpotent
81.(83.)		$N ( F ) = \{ g \in GL ( V ) : g v \equiv v \operatorname { mod } V _ { i } \text { for all } v \in V _ { i } , i \geq 1 \}$	$$\empty$$	conf 0.466 png = l0586604.png(4)
Lie group, semi-simple
82.(35.)*		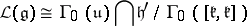$L ( \mathfrak { g } ) \cong \Gamma _ { 0 } ( \mathfrak { u } ) \cap \mathfrak { h } ^ { \prime } / \Gamma _ { 0 } ( [ \mathfrak { k } , \mathfrak { k } ] )$	$$\empty$$	conf 0.659 F png = l058680102.png(102)
83.(81.)*		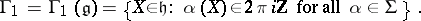$\Gamma _ { 1 } = \Gamma _ { 1 } ( g ) = \{ X \in h : \alpha ( X ) \in 2 \pi i Z \text { for all } \alpha \in \Sigma \}$	$$\empty$$	conf 0.183 F png = l05868032.png(32)
Lie p-algebra
84.(36.)		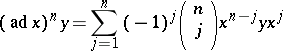$( \operatorname { ad } x ) ^ { n } y = \sum _ { j = 1 } ^ { n } ( - 1 ) ^ { j } \left( \begin{array} { c } { n } \\ { j } \end{array} \right) x ^ { n - j } y x ^ { j }$	$$\empty$$	conf 0.356 png = l05872026.png(26)
85.(99.)		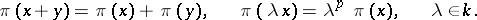$\pi ( x + y ) = \pi ( x ) + \pi ( y ) , \quad \pi ( \lambda x ) = \lambda ^ { p } \pi ( x ) , \quad \lambda \in k$	$$\empty$$	conf 0.964 png = l05872078.png(78)
Lie theorem
86.(134.)		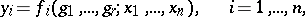$y _ { i } = f _ { i } ( g _ { 1 } , \ldots , g _ { i } || x _ { 1 } , \ldots , x _ { n } ) , \quad i = 1 , \ldots , n$	$$\empty$$	conf 0.276 png = l05876010.png(10)
87.(86.)		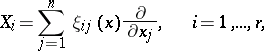$X _ { i } = \sum _ { j = 1 } ^ { n } \xi _ { i j } ( x ) \frac { \partial } { \partial x _ { j } } , \quad i = 1 , \ldots , r$	$$\empty$$	conf 0.656 png = l05876016.png(16)
88.(66.)*		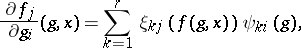$\frac { \partial f _ { j } } { \partial g _ { i } } ( g , x ) = \sum _ { k = 1 } ^ { r } \xi _ { k j } ( f ( g _ { s } x ) ) \psi _ { k i } ( g )$	$$\empty$$	conf 0.336 F png = l05876030.png(30)
89.(19.)*		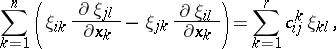$\sum _ { k = 1 } ^ { N } ( \xi _ { i k } \frac { \partial \xi _ { j l } } { \partial x _ { k } } - \xi _ { j k } \frac { \partial \xi _ { i l } } { \partial x _ { k } } ) = \sum _ { k = 1 } ^ { r } c _ { i j } ^ { k } \xi _ { k l }$	$$\empty$$	conf 0.157 F png = l05876037.png(37)
90.(14.)		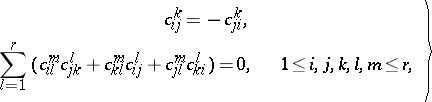$\left. \begin{array} { c } { c _ { i j } ^ { k } = - c _ { j i } ^ { k } } \\ { \sum _ { l = 1 } ^ { r } ( c _ { i l } ^ { m } c _ { j k } ^ { l } + c _ { k l } ^ { m } c _ { i j } ^ { l } + c _ { j l } ^ { m } c _ { k i } ^ { l } ) = 0 , \quad 1 \leq i , j , k , l , m \leq r } \end{array} \right.$	$$\empty$$	conf 0.085 png = l05876052.png(52)
Maximal torus
91.(95.)		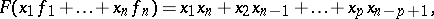$F ( x _ { 1 } f _ { 1 } + \ldots + x _ { x } f _ { n } ) = x _ { 1 } x _ { n } + x _ { 2 } x _ { n } - 1 + \ldots + x _ { p } x _ { n } - p + 1$	$$\empty$$	conf 0.198 png = m06301072.png(72)
Non-Abelian cohomology
92.(114.)*		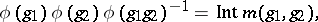$\phi ( g _ { 1 } ) \phi ( g ) \phi ( g _ { 1 } g _ { 2 } ) ^ { - 1 } = \operatorname { Int } m ( g _ { 1 } , g _ { 2 } )$	$$\empty$$	conf 0.443 F png = n066900110.png(110)
93.(90.)*		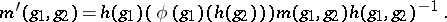$( g _ { 1 } , g _ { 2 } ) = h ( g _ { 1 } ) ( \phi ( g _ { 1 } ) ( h ( g _ { 2 } ) ) ) m ( g _ { 1 } , g _ { 2 } ) h ( g _ { 1 } , g _ { 2 } ) ^ { - 1 }$	$$\empty$$	conf 0.764 F png = n066900118.png(118)
94.(44.)		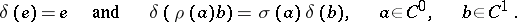$\delta ( e ) = e \quad \text { and } \quad \delta ( \rho ( a ) b ) = \sigma ( a ) \delta ( b ) , \quad \alpha \in C ^ { 0 } , \quad b \in C ^ { 1 }$	$$\empty$$	conf 0.400 png = n06690016.png(16)
95.(60.)*		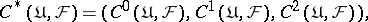$C ^ { * } ( \mathfrak { U } , F ) = ( C ^ { 0 } ( \mathfrak { U } , F ) , C ^ { 1 } ( \mathfrak { U } , F ) , C ^ { 2 } ( \mathfrak { U } , F ) )$	$$\empty$$	conf 0.205 F png = n06690028.png(28)
Picard scheme
96.(39.)*		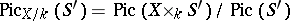$\operatorname { Pic } _ { X / k } ( S ^ { \prime } ) = \operatorname { Fic } ( X \times k S ^ { \prime } ) / \operatorname { Fic } ( S ^ { \prime } )$	$$\empty$$	conf 0.345 F + png = p07267025.png(25)
Principal analytic fibration
97.(100.)*		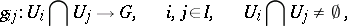$g j : U _ { i } \cap U _ { j } \rightarrow G , \quad i , j \in I , \quad U _ { i } \cap U _ { j } \neq \emptyset$	$$\empty$$	conf 0.184 F png = p07464025.png(25)
Quantum groups
98.(101.)		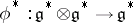$\phi ^ { * } : \mathfrak { g } ^ { * } \otimes \mathfrak { g } ^ { * } \rightarrow \mathfrak { g } ^ { * }$	$$\empty$$	conf 0.837 png = q07631062.png(62)
99.(108.)		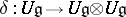$\delta : U _ { \mathfrak { g } } \rightarrow U _ { \mathfrak { g } } \otimes U _ { \mathfrak { g } }$	$$\empty$$	conf 0.648 png = q07631071.png(71)
100.(56.)*		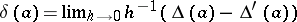$\delta ( \alpha ) = \operatorname { lim } _ { h \rightarrow 0 } h ^ { - 1 } ( \Delta ( a ) - \Delta ^ { \prime } ( \alpha ) )$	$$\empty$$	conf 0.304 F png = q07631072.png(72)
101.(129.)*		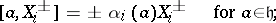$[ \alpha , X _ { i } ^ { \pm } ] = \pm \alpha _ { i } ( \alpha ) X _ { i } ^ { \pm } \quad \text { for } a$	$$\empty$$	conf 0.544 F png = q07631088.png(88)
102.(128.)		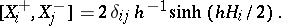$[ X _ { i } ^ { + } , X _ { j } ^ { - } ] = 2 \delta _ { i j } h ^ { - 1 } \operatorname { sinh } ( h H _ { i } / 2 )$	$$\empty$$	conf 0.893 png = q07631089.png(89)
103.(20.)		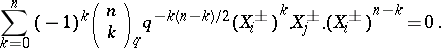$\sum _ { k = 0 } ^ { n } ( - 1 ) ^ { k } \left( \begin{array} { l } { n } \\ { k } \end{array} \right) q ^ { - k ( n - k ) / 2 } ( X _ { i } ^ { \pm } ) ^ { k } X _ { j } ^ { \pm } \cdot ( X _ { i } ^ { \pm } ) ^ { n - k } = 0$	$$\empty$$	conf 0.055 png = q07631092.png(92)
104.(30.)		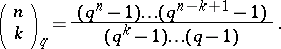$\left( \begin{array} { l } { n } \\ { k } \end{array} \right) _ { q } = \frac { ( q ^ { n } - 1 ) \ldots ( q ^ { n - k + 1 } - 1 ) } { ( q ^ { k } - 1 ) \ldots ( q - 1 ) }$	$$\empty$$	conf 0.443 png = q07631095.png(95)
105.(21.)*		$\Delta ( X _ { i } ^ { \pm } ) = X _ { i } ^ { \pm } \bigotimes \operatorname { exp } ( \frac { h H _ { i } } { 4 } ) + \operatorname { exp } ( \frac { - h H _ { i } } { 4 } ) \otimes x _ { i } ^ { \pm }$	$$\empty$$	conf 0.212 F png = q07631099.png(99)
Rational representation
106.(91.)		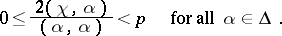$0 \leq \frac { 2 ( \chi , \alpha ) } { ( \alpha , \alpha ) } < p \quad \text { for all } \alpha \in \Delta$	$$\empty$$	conf 0.879 png = r077630100.png(100)
107.(135.)		$\phi _ { 0 } \bigotimes \phi _ { 1 } ^ { Fr } \otimes \ldots \otimes \phi _ { d } ^ { FF ^ { d } }$	$$\empty$$	conf 0.136 png = r077630104.png(104)
108.(45.)*		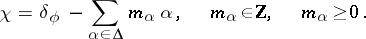$\chi = \delta _ { \phi } - \sum _ { \alpha \in \Delta } m _ { \alpha } \alpha , \quad m _ { \alpha } \in Z , \quad m _ { \alpha } \geq 0$	$$\empty$$	conf 0.862 F png = r07763055.png(55)
Singular point
109.(31.)		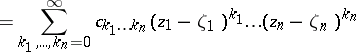$\sum _ { k _ { 1 } , \ldots , k _ { n } = 0 } ^ { \infty } c _ { k _ { 1 } \cdots k _ { n } } ( z _ { 1 } - \zeta _ { 1 } ) ^ { k _ { 1 } } \ldots ( z _ { n } - \zeta _ { n } ) ^ { k _ { n } }$	$$\empty$$	conf 0.324 png = s085590225.png(225)
110.(46.)		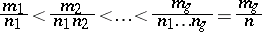$\frac { m _ { 1 } } { n _ { 1 } } < \frac { m _ { 2 } } { n _ { 1 } n _ { 2 } } < \ldots < \frac { m _ { g } } { n _ { 1 } \ldots n _ { g } } = \frac { m _ { g } } { n }$	$$\empty$$	conf 0.459 png = s085590404.png(404)
111.(115.)*		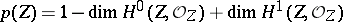$p ( Z ) = 1 - \operatorname { dim } H ^ { 0 } ( Z , O _ { Z } ) + \operatorname { dim } H ^ { 1 } ( Z , O _ { Z } )$	$$\empty$$	conf 0.997 F png = s085590429.png(429)
112.(136.)*		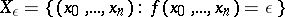$X _ { \epsilon } = \{ ( x _ { 0 } , \ldots , x _ { x } ) : f ( x _ { 0 } , \ldots , x _ { x } ) = \epsilon \}$	$$\empty$$	conf 0.433 F png = s085590440.png(440)
113.(12.)		$= \left\{ \begin{array} { l l } { ( x + \lambda ) ^ { 2 } \ldots ( x + k \lambda ) ^ { 2 } } & { \text { if } \mu = 2 k } \\ { ( x + \lambda ) ^ { 2 } \ldots ( x + k \lambda ) ^ { 2 } ( x + ( k + 1 ) \lambda ) } & { \text { if } \mu = 2 k + 1 } \end{array} \right.$	$$\empty$$	conf 0.870 png = s085590458.png(458)
114.(75.)		$( \frac { \partial F ( x , y , \lambda ) } { \partial x } , \frac { \partial F ( x , y , \lambda ) } { \partial y } )$	$$\empty$$	conf 0.986 png = s085590482.png(482)
115.(137.)		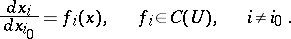$\frac { d x _ { i } } { d x _ { i _ { 0 } } } = f _ { i } ( x ) , \quad f _ { i } \in C ( U ) , \quad i \neq i _ { 0 }$	$$\empty$$	conf 0.594 png = s085590515.png(515)
116.(142.)*		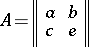$A = \| \left. \begin{array} { l l } { \alpha } & { b } \\ { c } & { e } \end{array} \right. |$	$$\empty$$	conf 0.506 F png = s085590527.png(527)
117.(53.)		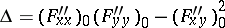$\Delta = ( F _ { x x } ^ { \prime \prime } ) _ { 0 } ( F _ { y y } ^ { \prime \prime } ) _ { 0 } - ( F _ { x y } ^ { \prime \prime } ) _ { 0 } ^ { 2 }$	$$\empty$$	conf 0.920 png = s085590634.png(634)
118.(16.)*		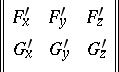$\left| \begin{array} { l l l } { F _ { X } ^ { \prime } } & { F _ { y } ^ { \prime } } & { F _ { z } ^ { \prime } } \\ { G _ { \chi } ^ { \prime } } & { G _ { y } ^ { \prime } } & { G _ { Z } ^ { \prime } } \end{array} \right|$	$$\empty$$	conf 0.230 F png = s085590645.png(645)
119.(92.)		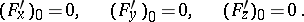$( F _ { X } ^ { \prime } ) _ { 0 } = 0 , \quad ( F _ { y } ^ { \prime } ) _ { 0 } = 0 , \quad ( F _ { z } ^ { \prime } ) _ { 0 } = 0$	$$\empty$$	conf 0.300 png = s085590653.png(653)
Solv manifold
120.(138.)		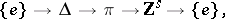$\{ e \} \rightarrow \Delta \rightarrow \pi \rightarrow Z ^ { s } \rightarrow \{ e \}$	$$\empty$$	conf 0.972 png = s08610054.png(54)
Stability theorems in algebraic K-theory
121.(71.)		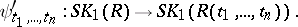$\psi _ { t _ { 1 } , \ldots , t _ { R } } ^ { \prime } : S K _ { 1 } ( R ) \rightarrow S K _ { 1 } ( R ( t _ { 1 } , \ldots , t _ { n } ) )$	$$\empty$$	conf 0.379 png = s08706033.png(33)
Steinberg module
122.(130.)		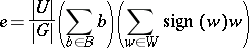$e = \frac { | U | } { | G | } ( \sum _ { b \in B } b ) ( \sum _ { w \in W } \operatorname { sign } ( w ) w )$	$$\empty$$	conf 0.138 png = s13053016.png(16)
Steinberg symbol
123.(24.)*		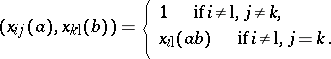$( x _ { i j } ( a ) , x _ { k l } ( b ) ) = \left\{ \begin{array} { l l } { 1 } & { \text { if } i \neq 1 , j \neq k } \\ { x _ { 1 } ( a b ) } & { \text { if } i \neq 1 , j = k } \end{array} \right.$	$$\empty$$	conf 0.381 F png = s13054017.png(17)
Tilting theory
124.(84.)		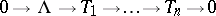$0 \rightarrow \Lambda \rightarrow T _ { 1 } \rightarrow \ldots \rightarrow T _ { n } \rightarrow 0$	$$\empty$$	conf 0.946 png = t130130105.png(105)
Tits quadratic form
125.(18.)		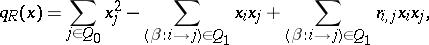$q R ( x ) = \sum _ { j \in Q _ { 0 } } x _ { j } ^ { 2 } - \sum _ { \langle \beta : i \rightarrow j ) \in Q _ { 1 } } x _ { i } x _ { j } + \sum _ { \langle \beta : i \rightarrow j ) \in Q _ { 1 } } x _ { , j } x _ { i } x _ { j }$	$$\empty$$	conf 0.112 png = t130140104.png(104)
126.(40.)		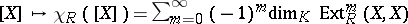$[ X ] \mapsto \chi _ { R } ( [ X ] ) = \sum _ { m = 0 } ^ { \infty } ( - 1 ) ^ { m } \operatorname { dim } _ { K } \operatorname { Ext } _ { R } ^ { m } ( X , X )$	$$\empty$$	conf 0.116 png = t130140118.png(118)
127.(132.)*		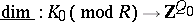$\operatorname { dim } _ { 1 } : K _ { 0 } ( \operatorname { mod } R ) \rightarrow Z ^ { Q _ { 0 } }$	$$\empty$$	conf 0.287 F png = t130140119.png(119)
128.(37.)*		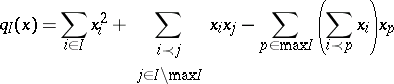$q ( x ) = \sum _ { i \in I } x _ { i } ^ { 2 } + \sum _ { i \prec j } x _ { i } x _ { j } - \sum _ { p \in \operatorname { max } l } ( \sum _ { i \prec p } x _ { i } ) x _ { p }$	$$\empty$$	conf 0.197 F png = t130140140.png(140)
129.(131.)*		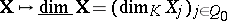$X \mapsto \operatorname { dim } X = ( \operatorname { dim } _ { K } X _ { j } ) _ { j \in Q _ { 0 } }$	$$\empty$$	conf 0.819 F png = t13014044.png(44)
130.(25.)		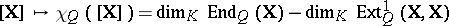$[ X ] \mapsto \chi _ { Q } ( [ X ] ) = \operatorname { dim } _ { K } \operatorname { End } _ { Q } ( X ) - \operatorname { dim } _ { K } \operatorname { Ext } _ { Q } ^ { 1 } ( X , X )$	$$\empty$$	conf 0.661 png = t13014048.png(48)
131.(38.)*		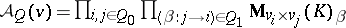$A _ { Q } ( v ) = \prod _ { i , j \in Q _ { 0 } } \prod _ { \langle \beta : j \rightarrow i \rangle \in Q _ { 1 } } M _ { v _ { i } \times v _ { j } } ( K ) _ { \beta }$	$$\empty$$	conf 0.481 F png = t13014056.png(56)
132.(139.)*		$\Phi ( x ) = \sum _ { j \in Q _ { 0 } } x _ { j } ^ { 2 } - \sum _ { i , j \in Q _ { 0 } } d _ { i j } x _ { i } x _ { j }$	$$\empty$$	conf 0.648 F png = t1301406.png(6)
Torus
133.(41.)*		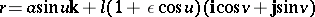$r = \alpha \operatorname { sin } u k + l ( 1 + \epsilon \operatorname { cos } u ) ( i \operatorname { cos } v + j \operatorname { sin } v )$	$$\empty$$	conf 0.585 F png = t0933502.png(2)
134.(122.)*		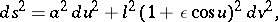$d s ^ { 2 } = \alpha ^ { 2 } d u ^ { 2 } + l ^ { 2 } ( 1 + \epsilon \operatorname { cos } u ) ^ { 2 } d v ^ { 2 }$	$$\empty$$	conf 0.696 F png = t0933507.png(7)
Uniform distribution
135.(9.)		$u _ { 3 } ( x ) = \left\{ \begin{array} { l l } { \frac { x ^ { 2 } } { 2 } , } & { 0 \leq x < 1 } \\ { \frac { [ x ^ { 2 } - 3 ( x - 1 ) ^ { 2 } ] } { 2 } , } & { 1 \leq x < 2 } \\ { \frac { [ x ^ { 2 } - 3 ( x - 1 ) ^ { 2 } + 3 ( x - 2 ) ^ { 2 } ] } { 2 } , } & { 2 \leq x < 3 } \\ { 0 , } & { x \notin [ 0,3 ] } \end{array} \right.$	$$\empty$$	conf 0.733 png = u09524027.png(27)
136.(32.)*		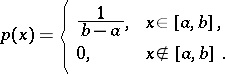$p ( x ) = \left\{ \begin{array} { l l } { \frac { 1 } { b - \alpha } , } & { x \in [ \alpha , b ] } \\ { 0 , } & { x \notin [ \alpha , b ] } \end{array} \right.$	$$\empty$$	conf 0.681 F png = u0952403.png(3)
137.(34.)		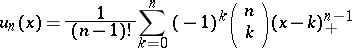$u _ { n } ( x ) = \frac { 1 } { ( n - 1 ) ! } \sum _ { k = 0 } ^ { n } ( - 1 ) ^ { k } \left( \begin{array} { l } { n } \\ { k } \end{array} \right) ( x - k ) _ { + } ^ { n - 1 }$	$$\empty$$	conf 0.569 png = u09524030.png(30)
138.(109.)		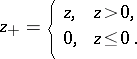$z _ { + } = \left\{ \begin{array} { l l } { z , } & { z > 0 } \\ { 0 , } & { z \leq 0 } \end{array} \right.$	$$\empty$$	conf 0.676 png = u09524034.png(34)
139.(43.)		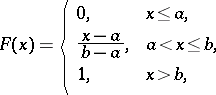$F ( x ) = \left\{ \begin{array} { l l } { 0 , } & { x \leq a } \\ { \frac { x - a } { b - a } , } & { a < x \leq b } \\ { 1 , } & { x > b } \end{array} \right.$	$$\empty$$	conf 0.468 png = u0952407.png(7)
140.(47.)		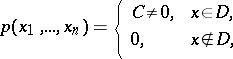$p ( x _ { 1 } , \ldots , x _ { n } ) = \left\{ \begin{array} { l l } { C \neq 0 , } & { x \in D } \\ { 0 , } & { x \notin D } \end{array} \right.$	$$\empty$$	conf 0.705 png = u09524072.png(72)
Unipotent group
141.(143.)		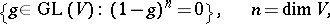$\{ g \in \operatorname { GL } ( V ) : ( 1 - g ) ^ { n } = 0 \} , \quad n = \operatorname { dim } V$	$$\empty$$	conf 0.287 png = u0954106.png(6)
Weyl module
142.(51.)		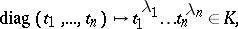$\operatorname { diag } ( t _ { 1 } , \ldots , t _ { n } ) \mapsto t _ { 1 } ^ { \lambda _ { 1 } } \ldots t _ { n } ^ { \lambda _ { n } } \in K$	$$\empty$$	conf 0.507 png = w120090122.png(122)
143.(54.)*		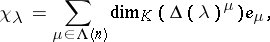$\chi _ { \lambda } = \sum _ { \mu \in \Lambda ( n ) } \operatorname { dim } _ { K } ( \Delta ( \lambda ) ^ { \mu } ) _ { e _ { \mu } }$	$$\empty$$	conf 0.461 F png = w120090135.png(135)
144.(110.)		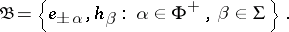$\mathfrak { B } = \{ e _ { \pm } \alpha , h _ { \beta } : \alpha \in \Phi ^ { + } , \beta \in \Sigma \}$	$$\empty$$	conf 0.381 png = w120090259.png(259)
145.(82.)		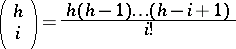$\left( \begin{array} { c } { h } \\ { i } \end{array} \right) = \frac { h ( h - 1 ) \ldots ( h - i + 1 ) } { i ! }$	$$\empty$$	conf 0.487 png = w120090342.png(342)
146.(28.)*		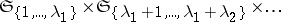$\mathfrak { S } _ { \{ 1 , \ldots , \lambda _ { 1 } \} } \times \mathfrak { S } _ { \{ \lambda _ { 1 } + 1 , \ldots , \lambda _ { 1 } + \lambda _ { 2 } \} } \times$	$$\empty$$	conf 0.312 F png = w12009095.png(95)
147.(104.)		$\ldots \times \mathfrak { S } _ { \{ \lambda _ { 1 } + \ldots + \lambda _ { n - 1 } + 1 , \ldots , r \} }$	$$\empty$$	conf 0.259 png = w12009096.png(96)
Witt vector
148.(87.)*		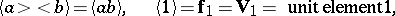$\langle \alpha > < b \rangle = \langle \alpha b \rangle , \quad \langle 1 \rangle = f _ { 1 } = V _ { 1 } =$	$$\empty$$	conf 0.351 F png = w098100172.png(172)
149.(123.)*		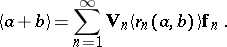$\langle \alpha + b \rangle = \sum _ { n = 1 } ^ { \infty } V _ { n } \langle r _ { n } ( \alpha , b ) f$	$$\empty$$	conf 0.143 F png = w098100177.png(177)
150.(102.)		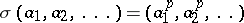$\sigma ( \alpha _ { 1 } , \alpha _ { 2 } , \ldots ) = ( \alpha _ { 1 } ^ { p } , \alpha _ { 2 } ^ { p } , \ldots )$	$$\empty$$	conf 0.771 png = w098100190.png(190)