Difference between revisions of "Closed monoidal category"
(Importing text file) |
(TeX partly done) |
||
| Line 1: | Line 1: | ||
| − | A [[ | + | A [[category]] $\mathcal{C}$ is monoidal if it consists of the following data: |
| − | 1) a category | + | 1) a category $\mathcal{C}$; |
| − | 2) a [[ | + | 2) a [[bifunctor]] $\otimes : \mathcal{C}\times\mathcal{C}\rightarrow\mathcal{C}$; |
| − | 3) an object | + | 3) an object $e\in\mathcal{C}$; and |
| − | 4) three natural isomorphisms | + | 4) three natural isomorphisms $\alpha,\lambda,\rho$ such that |
| − | A1) | + | A1) $\alpha_{a,b,c} : a \otimes (b \otimes c) \cong (a \otimes b) \otimes c$ is natural for all $a,b,c \in \mathcal{C}$ and the diagram |
| + | $$ | ||
| + | \begin{array}{ccccc} | ||
| + | a \otimes (b \otimes (c \otimes d)) & \stackrel{\alpha}{\rightarrow} & (a \otimes b) \otimes (c \otimes d) & \stackrel{\alpha}{\rightarrow} & ((a \otimes b) \otimes c) \otimes d \\ | ||
| + | \downarrow\mathrm{id}\otimes\alpha & & & & \uparrow \alpha\otimes\mathrm{id} \\ | ||
| + | a \otimes ((b \otimes c) \otimes d) & & \stackrel{\alpha}{\rightarrow} & & (a \otimes (b \otimes c)) \otimes d | ||
| + | \end{array} | ||
| + | $$ | ||
| + | commutes for all $a,b,c,d \in \mathcal{C}$; | ||
| − | + | A2) $\lambda$ and $\rho$ are natural and $\lambda : e \otimes a \cong a$, $\rho : a \otimes e \cong a$ for all objects $a \in \mathcal{C}$ and the diagram | |
| + | $$ | ||
| + | \begin{array}{ccc} | ||
| + | a \otimes (e \otimes c) & \stackrel{\alpha}{\rightarrow} & (a \otimes e) \otimes c \\ | ||
| + | \downarrow\mathrm{id}\otimes\lambda & & \downarrow\rho\otimes\mathrm{id} \\ | ||
| + | a \otimes c & = & a \otimes c | ||
| + | \end{array} | ||
| + | $$ | ||
| + | commutes for all $a.c \in \mathcal{C}$; | ||
| − | + | A3) $\lambda_e = \rho_e : e \otimes e \rightarrow e$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | A3) | ||
These axioms imply that all such diagrams commute. | These axioms imply that all such diagrams commute. | ||
| Line 27: | Line 35: | ||
Some examples of monoidal categories are: | Some examples of monoidal categories are: | ||
| − | E1) any category with finite products is monoidal if one takes | + | E1) any category with finite products is monoidal if one takes $a\otimes b$ to be the (chosen) product of the objects $a$ and $b$, with $e$ the terminal object; $\alpha,\lambda,\rho$ are the unique isomorphisms that commute with the appropriate projections; |
| − | E2) the usual "tensor products" give monoidal categories — whence the notation. Note that one cannot identify all isomorphic objects in | + | E2) the usual "tensor products" give monoidal categories — whence the notation. Note that one cannot identify all isomorphic objects in $\mathcal{C}$. |
==Closed categories.== | ==Closed categories.== | ||
| Line 47: | Line 55: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> M. Barr, C. Wells, "Category theory for computing science" , CRM (1990)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> S. MacLane, "Categories for the working mathematician" , Springer (1971)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> M. Barr, C. Wells, "Category theory for computing science" , CRM (1990)</TD></TR> | ||
| + | <TR><TD valign="top">[a2]</TD> <TD valign="top"> S. MacLane, "Categories for the working mathematician" , Springer (1971)</TD></TR> | ||
| + | </table> | ||
| + | |||
| + | {{TEX|part}} | ||
Revision as of 19:46, 30 November 2017
A category $\mathcal{C}$ is monoidal if it consists of the following data:
1) a category $\mathcal{C}$;
2) a bifunctor $\otimes : \mathcal{C}\times\mathcal{C}\rightarrow\mathcal{C}$;
3) an object $e\in\mathcal{C}$; and
4) three natural isomorphisms $\alpha,\lambda,\rho$ such that
A1) $\alpha_{a,b,c} : a \otimes (b \otimes c) \cong (a \otimes b) \otimes c$ is natural for all $a,b,c \in \mathcal{C}$ and the diagram $$ \begin{array}{ccccc} a \otimes (b \otimes (c \otimes d)) & \stackrel{\alpha}{\rightarrow} & (a \otimes b) \otimes (c \otimes d) & \stackrel{\alpha}{\rightarrow} & ((a \otimes b) \otimes c) \otimes d \\ \downarrow\mathrm{id}\otimes\alpha & & & & \uparrow \alpha\otimes\mathrm{id} \\ a \otimes ((b \otimes c) \otimes d) & & \stackrel{\alpha}{\rightarrow} & & (a \otimes (b \otimes c)) \otimes d \end{array} $$ commutes for all $a,b,c,d \in \mathcal{C}$;
A2) $\lambda$ and $\rho$ are natural and $\lambda : e \otimes a \cong a$, $\rho : a \otimes e \cong a$ for all objects $a \in \mathcal{C}$ and the diagram $$ \begin{array}{ccc} a \otimes (e \otimes c) & \stackrel{\alpha}{\rightarrow} & (a \otimes e) \otimes c \\ \downarrow\mathrm{id}\otimes\lambda & & \downarrow\rho\otimes\mathrm{id} \\ a \otimes c & = & a \otimes c \end{array} $$ commutes for all $a.c \in \mathcal{C}$;
A3) $\lambda_e = \rho_e : e \otimes e \rightarrow e$.
These axioms imply that all such diagrams commute.
Some examples of monoidal categories are:
E1) any category with finite products is monoidal if one takes $a\otimes b$ to be the (chosen) product of the objects $a$ and $b$, with $e$ the terminal object; $\alpha,\lambda,\rho$ are the unique isomorphisms that commute with the appropriate projections;
E2) the usual "tensor products" give monoidal categories — whence the notation. Note that one cannot identify all isomorphic objects in $\mathcal{C}$.
Closed categories.
A monoidal category 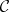 is said to be symmetric if it comes with isomorphisms
is said to be symmetric if it comes with isomorphisms 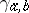 :
:  natural on
natural on 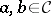 such that the following diagrams all commute:
such that the following diagrams all commute:
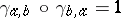 ,
, 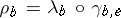 :
: 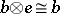 :
:
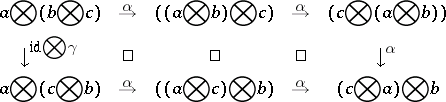 |
A closed category  is a symmetric monoidal category in which each functor
is a symmetric monoidal category in which each functor  has a specified right-adjoint
has a specified right-adjoint 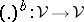 .
.
Some examples of closed monoidal categories are:
E3) the category 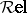 of relations, whose objects are sets
of relations, whose objects are sets  and in which an arrow
and in which an arrow 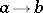 is a subset
is a subset 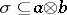 ; the object
; the object 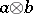 is the Cartesian product of the two sets, which is not the product in this category;
is the Cartesian product of the two sets, which is not the product in this category;
E4) the subsets of a monoid 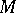 (a poset, hence a category); if
(a poset, hence a category); if 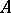 ,
, 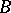 are two subsets of
are two subsets of 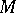 , then
, then 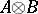 is
is  while
while 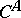 is
is 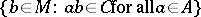 .
.
References
| [a1] | M. Barr, C. Wells, "Category theory for computing science" , CRM (1990) |
| [a2] | S. MacLane, "Categories for the working mathematician" , Springer (1971) |
Closed monoidal category. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Closed_monoidal_category&oldid=42386