Difference between revisions of "Direct product"
(mention restricted direct product) |
(TeX partly done) |
||
| Line 1: | Line 1: | ||
{{MSC|03E}} | {{MSC|03E}} | ||
| − | A basic general mathematical construction. The idea behind it is due to R. Descartes; therefore the direct product is also called the Cartesian product. The direct product, or simply the product, of two non-empty sets | + | A basic general mathematical construction. The idea behind it is due to R. Descartes; therefore the direct product is also called the Cartesian product. The direct product, or simply the product, of two non-empty sets $X$ and $Y$ is the set $X \times Y$ consisting of all [[ordered pair]]s of the form $(x,y)$, $x \in X$, $y \in Y$: |
| + | $$ | ||
| + | X \times Y = \{ (x,y) : x \in X\,\ y \in Y \} \ . | ||
| + | $$ | ||
| − | + | If one of the sets $X$ or $Y$ is empty then so is their product. The set $X \times Y$ can be identified with the set of functions defined on the two-element set $\{1,2\}$ and taking the value $1$ to elements of $X$, and the value $2$ to elements of $Y$. This identification leads to a general definition of a direct product of sets. Let $I$ be some index set and suppose that $X_i$ is an arbitrary family of sets, indexed by the elements of $I$. The direct product of the $X_i$, $i \in I$, is the set of functions $f : I \rightarrow X$, where $X = \bigcup_{i\in I} X_i$, such that $f(i) \in X_i$ for every $i \in I$. Usually, the direct product is denoted by $\prod_{i\in I} X_i$, for a finite index set $I = \{1,\ldots,n\}$ one also uses the notations $\prod_{i=1}^n X_i$ and $X_1 \times \cdots \times X_n$. If $I$ consists of the single element $\{1\}$, then $\prod_I X_i = X_1$. Sometimes one defines the direct product of a finite number of factors inductively: | |
| + | $$ | ||
| + | \prod_{i=1} X_i = X_1 \ ; | ||
| + | $$ | ||
| + | $$ | ||
| + | \prod_{i=1}^{n+1} = \left({ \prod_{i=1}^n X_i }\right) \times X_{n+1} \ . | ||
| + | $$ | ||
| − | + | One merit of the construction of a direct product rests above all in the possibility of naturally introducing supplementary structures in it, if all factors have the same mathematical structure. E.g., if the $X_i$, $i \in I$, are [[algebraic system]]s of the same type, i.e. sets with a common [[signature]] of finitely-placed predicates and operations, then the product $\prod_{i\in I} X_i$ can be made into an algebraic system of the same signature: For functions $f_1,\ldots,f_k : I \rightarrow X$ and a $k$-ary operation $\omega$ the action of the function $f_1,\ldots,f_k\,\omega$ on one element $i\in I$ is defined by | |
| + | $$ | ||
| + | f_1,\ldots,f_k\,\omega (i) = f_1(i),\ldots,f_k(i)\,\omega \ . | ||
| + | $$ | ||
| − | + | The value of a predicate $P(f_1,\ldots,f_k)$ is true if for every $i \in I$ the value of $P(f_1(i),\ldots,f_k(i))$ is true. Moreover, if in all $X_i$ an equation is satisfied, then it is also satisfied in their product. Therefore, the product of semi-groups, groups, rings, vector spaces, etc., is again a semi-group, group, ring, vector space, respectively. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | The value of a predicate | ||
For an arbitrary factor of a direct product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273044.png" /> there exists a natural projection <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273045.png" />, defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273046.png" />. The set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273047.png" /> and the family of projections <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273048.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273049.png" />, have the following universal property: For every family of mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273050.png" /> there exists a unique mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273051.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273052.png" /> for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273053.png" />. This property also holds if all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273054.png" /> are algebraic systems of one type, and makes it possible to define a suitable topology on a direct product of topological spaces. The property formulated is the basis for the definition of the [[product of a family of objects in a category]]. | For an arbitrary factor of a direct product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273044.png" /> there exists a natural projection <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273045.png" />, defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273046.png" />. The set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273047.png" /> and the family of projections <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273048.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273049.png" />, have the following universal property: For every family of mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273050.png" /> there exists a unique mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273051.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273052.png" /> for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273053.png" />. This property also holds if all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273054.png" /> are algebraic systems of one type, and makes it possible to define a suitable topology on a direct product of topological spaces. The property formulated is the basis for the definition of the [[product of a family of objects in a category]]. | ||
| Line 22: | Line 26: | ||
The direct product is sometimes called the complete direct product, to distinguish it from the [[restricted direct product]], which is defined when there is a supplementary structure in the factors: an important case of this is the discrete direct product (or [[direct sum]]), which is defined when the supplementary structures are a one-element substructures (e.g. base points of [[pointed set]]s and [[pointed space]]s, unit subgroups of groups, zero subspaces, etc.). As a rule, the direct product of a finite number of factors coincides with the discrete product. | The direct product is sometimes called the complete direct product, to distinguish it from the [[restricted direct product]], which is defined when there is a supplementary structure in the factors: an important case of this is the discrete direct product (or [[direct sum]]), which is defined when the supplementary structures are a one-element substructures (e.g. base points of [[pointed set]]s and [[pointed space]]s, unit subgroups of groups, zero subspaces, etc.). As a rule, the direct product of a finite number of factors coincides with the discrete product. | ||
| + | |||
| + | {{TEX|part}} | ||
Revision as of 20:11, 7 February 2017
2020 Mathematics Subject Classification: Primary: 03E [MSN][ZBL]
A basic general mathematical construction. The idea behind it is due to R. Descartes; therefore the direct product is also called the Cartesian product. The direct product, or simply the product, of two non-empty sets $X$ and $Y$ is the set $X \times Y$ consisting of all ordered pairs of the form $(x,y)$, $x \in X$, $y \in Y$: $$ X \times Y = \{ (x,y) : x \in X\,\ y \in Y \} \ . $$
If one of the sets $X$ or $Y$ is empty then so is their product. The set $X \times Y$ can be identified with the set of functions defined on the two-element set $\{1,2\}$ and taking the value $1$ to elements of $X$, and the value $2$ to elements of $Y$. This identification leads to a general definition of a direct product of sets. Let $I$ be some index set and suppose that $X_i$ is an arbitrary family of sets, indexed by the elements of $I$. The direct product of the $X_i$, $i \in I$, is the set of functions $f : I \rightarrow X$, where $X = \bigcup_{i\in I} X_i$, such that $f(i) \in X_i$ for every $i \in I$. Usually, the direct product is denoted by $\prod_{i\in I} X_i$, for a finite index set $I = \{1,\ldots,n\}$ one also uses the notations $\prod_{i=1}^n X_i$ and $X_1 \times \cdots \times X_n$. If $I$ consists of the single element $\{1\}$, then $\prod_I X_i = X_1$. Sometimes one defines the direct product of a finite number of factors inductively: $$ \prod_{i=1} X_i = X_1 \ ; $$ $$ \prod_{i=1}^{n+1} = \left({ \prod_{i=1}^n X_i }\right) \times X_{n+1} \ . $$
One merit of the construction of a direct product rests above all in the possibility of naturally introducing supplementary structures in it, if all factors have the same mathematical structure. E.g., if the $X_i$, $i \in I$, are algebraic systems of the same type, i.e. sets with a common signature of finitely-placed predicates and operations, then the product $\prod_{i\in I} X_i$ can be made into an algebraic system of the same signature: For functions $f_1,\ldots,f_k : I \rightarrow X$ and a $k$-ary operation $\omega$ the action of the function $f_1,\ldots,f_k\,\omega$ on one element $i\in I$ is defined by $$ f_1,\ldots,f_k\,\omega (i) = f_1(i),\ldots,f_k(i)\,\omega \ . $$
The value of a predicate $P(f_1,\ldots,f_k)$ is true if for every $i \in I$ the value of $P(f_1(i),\ldots,f_k(i))$ is true. Moreover, if in all $X_i$ an equation is satisfied, then it is also satisfied in their product. Therefore, the product of semi-groups, groups, rings, vector spaces, etc., is again a semi-group, group, ring, vector space, respectively.
For an arbitrary factor of a direct product  there exists a natural projection
there exists a natural projection  , defined by
, defined by 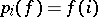 . The set
. The set 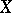 and the family of projections
and the family of projections 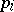 ,
, 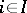 , have the following universal property: For every family of mappings
, have the following universal property: For every family of mappings 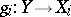 there exists a unique mapping
there exists a unique mapping  such that
such that  for every
for every 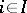 . This property also holds if all
. This property also holds if all  are algebraic systems of one type, and makes it possible to define a suitable topology on a direct product of topological spaces. The property formulated is the basis for the definition of the product of a family of objects in a category.
are algebraic systems of one type, and makes it possible to define a suitable topology on a direct product of topological spaces. The property formulated is the basis for the definition of the product of a family of objects in a category.
One often encounters problems of describing mathematical objects that cannot be decomposed into a direct product, and of stating conditions under which the factors of a direct product are uniquely determined up to an isomorphism. Classical results in this respect are the theorem on the structure of finitely-generated modules over principal ideal rings and the Remak–Schmidt theorem on the central isomorphism of direct decompositions of a group with a principal series.
The direct product is sometimes called the complete direct product, to distinguish it from the restricted direct product, which is defined when there is a supplementary structure in the factors: an important case of this is the discrete direct product (or direct sum), which is defined when the supplementary structures are a one-element substructures (e.g. base points of pointed sets and pointed spaces, unit subgroups of groups, zero subspaces, etc.). As a rule, the direct product of a finite number of factors coincides with the discrete product.
Direct product. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Direct_product&oldid=40201