Difference between revisions of "Ordered semi-group"
m (link) |
(TeX partly done) |
||
| Line 1: | Line 1: | ||
| − | A [[ | + | A [[semi-group]] equipped with a (generally speaking, partial) [[Order (on a set)|order]] $\le$ which is stable relative to the semi-group operation, i.e. for any elements $a,b,c$ it follows from $a \le b$ that $ac \le bc$ and $ca \le cb$. If the relation $\le$ on the ordered semi-group $S$ is a [[total order]], then $S$ is called a totally ordered semi-group (cf. also [[Totally ordered set]]). If the relation $\le$ on $S$ defines a [[lattice]] (with the associated operations join $\vee$ and meet $\wedge$) satisfying the identities |
| − | + | $$ | |
| − | + | c(a \vee b) = ca \vee cb\ \ \text{and}\ \ (a \vee b)c = ac \vee bc | |
| − | + | $$ | |
| − | then | + | then $S$ is called a lattice-ordered semi-group; thus, the class of all lattice-ordered semi-groups, considered as algebras with semi-group and lattice operations, is a variety (cf. also [[Variety of groups]]). On a lattice-ordered semi-group the identities |
| − | + | $$ | |
| − | + | c(a \wedge b) = ca \wedge cb\ \ \text{and}\ \ (a \wedge b)c = ac \wedge bc | |
| − | + | $$ | |
| − | generally speaking, | + | generally speaking, are not required to hold, and their imposition singles out a proper subvariety of the variety of all lattice-ordered semi-groups. |
Ordered semi-groups arise by considering different numerical semi-groups, semi-groups of functions and binary relations, semi-groups of subsets (or subsystems of different algebraic systems, for example ideals in rings and semi-groups), etc. Every ordered semi-group is isomorphic to a certain semi-group of binary relations, considered as an ordered semi-group, where the order is set-theoretic inclusion. The classical example of a lattice-ordered semi-group is the semi-group of all binary relations on an arbitrary set. | Ordered semi-groups arise by considering different numerical semi-groups, semi-groups of functions and binary relations, semi-groups of subsets (or subsystems of different algebraic systems, for example ideals in rings and semi-groups), etc. Every ordered semi-group is isomorphic to a certain semi-group of binary relations, considered as an ordered semi-group, where the order is set-theoretic inclusion. The classical example of a lattice-ordered semi-group is the semi-group of all binary relations on an arbitrary set. | ||
| − | In the general theory of ordered semi-groups one can distinguish two main developments: the theory of totally ordered semi-groups and the theory of lattice-ordered semi-groups. Although every totally ordered semi-group is lattice-ordered, both theories have developed to a large degree independently. The study of totally ordered semi-groups is devoted to properties that are to a large extent not shared by lattice-ordered semi-groups, while in considering lattice-ordered semi-groups one studies as a rule properties which, when applied to totally ordered semi-groups, reduce to degenerate cases. An important type of semi-groups is formed by the ordered groups (cf. [[Ordered group|Ordered group]]); their theory forms an independent part of algebra. In distinction to ordered groups, the order relation on an arbitrary ordered semi-group | + | In the general theory of ordered semi-groups one can distinguish two main developments: the theory of totally ordered semi-groups and the theory of lattice-ordered semi-groups. Although every totally ordered semi-group is lattice-ordered, both theories have developed to a large degree independently. The study of totally ordered semi-groups is devoted to properties that are to a large extent not shared by lattice-ordered semi-groups, while in considering lattice-ordered semi-groups one studies as a rule properties which, when applied to totally ordered semi-groups, reduce to degenerate cases. An important type of semi-groups is formed by the ordered groups (cf. [[Ordered group|Ordered group]]); their theory forms an independent part of algebra. In distinction to ordered groups, the order relation on an arbitrary ordered semi-group $S$ is, generally speaking, not defined by the set of its positive elements (i.e. the elements $a$ such that $ax \ge x$ and $xa \ge x$ for any $x$). |
==Totally ordered semi-groups.== | ==Totally ordered semi-groups.== | ||
| − | A semi-group | + | A semi-group $S$ is called ''orderable'' if one can define on it a total order which turns it into a totally ordered semi-group. A necessary condition for orderability is the absence in the semi-group of non-idempotent elements of finite order. If in an orderable semi-group the set of all idempotents is non-empty, then it is a sub-semi-group. Among the orderable semi-groups are the free semi-groups, the free commutative semi-groups, and the free $n$-step nilpotent semi-groups. There exists a continuum of methods for ordering free semi-groups of finite rank $\ge 2$. Certain necessary and sufficient conditions for the orderability of arbitrary semi-groups have been found, as well as for semi-groups from a series of known classes (e.g. semi-groups of idempotents, inverse semi-groups). |
| − | The structure of totally ordered semi-groups of idempotents has been completely described; in particular, the decomposition of such semi-groups into semi-lattices of rectangular semi-groups (cf. [[ | + | The structure of totally ordered semi-groups of idempotents has been completely described; in particular, the decomposition of such semi-groups into semi-lattices of rectangular semi-groups (cf. [[Idempotents, semi-group of]]) whose rectangular components are singular while the corresponding semi-lattices are trees. The completely-simple totally ordered semi-groups are exhausted by the [[right group]]s and the left groups and are lexicographic products (cf. [[Lexicographic order]]) of totally ordered groups and totally ordered semi-groups of right (respectively, left) zeros. By applying the reduction to totally ordered groups, a description of totally ordered semi-groups has been obtained in terms of the class of [[Clifford semi-group]]s, as well as a characterization in this way of the inverse totally ordered semi-groups (cf. [[Inversion semi-group]]). All types of totally ordered semi-groups generated by two mutually inverse elements have been classified (cf. [[Regular element]]). |
| − | The conditions imposed in the study of totally ordered semi-groups often postulate additional connections between the operation and the order relation. In this way one distinguishes the following basic types of totally ordered semi-groups: | + | The conditions imposed in the study of totally ordered semi-groups often postulate additional connections between the operation and the order relation. In this way one distinguishes the following basic types of totally ordered semi-groups: [[Archimedean semi-group]]s, naturally totally ordered semi-groups (cf. [[Naturally ordered groupoid|Naturally ordered groupoid]]), positive ordered semi-groups (in which all elements are positive), integral totally ordered semi-groups (in which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070150/o07015024.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070150/o07015025.png" />). Every Archimedean naturally totally ordered semi-group is commutative; their structure is completely described. The structure of an arbitrary totally ordered semi-group is to a large extent determined by the peculiarities of its decomposition into Archimedean classes (cf. [[Archimedean class|Archimedean class]]). For a periodic totally ordered semi-group this decomposition coincides with the decomposition into torsion classes, and, moreover, each Archimedean class is a [[Nil semi-group|nil semi-group]]. An arbitrary totally ordered nil semi-group is the union of an increasing sequence of convex nilpotent sub-semi-groups; in particular, it is locally nilpotent. |
A [[Homomorphism|homomorphism]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070150/o07015026.png" /> of totally ordered semi-groups is called an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070150/o07015028.png" />-homomorphism if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070150/o07015029.png" /> is an [[Isotone mapping|isotone mapping]] from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070150/o07015030.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070150/o07015031.png" />. A congruence (cf. [[Congruence (in algebra)|Congruence (in algebra)]]) on a totally ordered semi-group is called an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070150/o07015033.png" />-congruence if all its classes are convex subsets; the kernel congruences of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070150/o07015034.png" />-homomorphisms are precisely the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070150/o07015035.png" />-congruences. The decomposition of a totally ordered semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070150/o07015036.png" /> into Archimedean classes does not always define <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070150/o07015037.png" />-congruences, i.e. they are not always a band (cf. [[Band of semi-groups|Band of semi-groups]]), but this is so, for example, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070150/o07015038.png" /> is periodic and its idempotents commute or if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070150/o07015039.png" /> is a positive totally ordered semi-group. | A [[Homomorphism|homomorphism]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070150/o07015026.png" /> of totally ordered semi-groups is called an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070150/o07015028.png" />-homomorphism if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070150/o07015029.png" /> is an [[Isotone mapping|isotone mapping]] from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070150/o07015030.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070150/o07015031.png" />. A congruence (cf. [[Congruence (in algebra)|Congruence (in algebra)]]) on a totally ordered semi-group is called an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070150/o07015033.png" />-congruence if all its classes are convex subsets; the kernel congruences of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070150/o07015034.png" />-homomorphisms are precisely the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070150/o07015035.png" />-congruences. The decomposition of a totally ordered semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070150/o07015036.png" /> into Archimedean classes does not always define <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070150/o07015037.png" />-congruences, i.e. they are not always a band (cf. [[Band of semi-groups|Band of semi-groups]]), but this is so, for example, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070150/o07015038.png" /> is periodic and its idempotents commute or if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070150/o07015039.png" /> is a positive totally ordered semi-group. | ||
| Line 32: | Line 32: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> L. Fuchs, "Partially ordered algebraic systems" , Pergamon (1963)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> G. Birkhoff, "Lattice theory" , ''Colloq. Publ.'' , '''25''' , Amer. Math. Soc. (1973)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A.I. Kokorin, V.M. Kopytov, "Fully ordered groups" , Israel Program Sci. Transl. (1974) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> ''Itogi Nauk. Algebra. Topol. Geom. 1965'' (1967) pp. 116–120</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> ''Itogi Nauk. Algebra. Topol. Geom. 1966'' (1968) pp. 99–102</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> M. Satyanarayana, "Positively ordered semigroups" , M. Dekker (1979)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> E.Ya. Gabovich, "Fully ordered semigroups and their applications" ''Russian Math. Surveys'' , '''31''' : 1 (1976) pp. 147–216 ''Uspekhi Mat. Nauk'' , '''31''' : 1 (1976) pp. 137–201</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> L. Fuchs, "Partially ordered algebraic systems" , Pergamon (1963)</TD></TR> | ||
| + | <TR><TD valign="top">[2]</TD> <TD valign="top"> G. Birkhoff, "Lattice theory" , ''Colloq. Publ.'' , '''25''' , Amer. Math. Soc. (1973)</TD></TR> | ||
| + | <TR><TD valign="top">[3]</TD> <TD valign="top"> A.I. Kokorin, V.M. Kopytov, "Fully ordered groups" , Israel Program Sci. Transl. (1974) (Translated from Russian)</TD></TR> | ||
| + | <TR><TD valign="top">[4]</TD> <TD valign="top"> ''Itogi Nauk. Algebra. Topol. Geom. 1965'' (1967) pp. 116–120</TD></TR> | ||
| + | <TR><TD valign="top">[5]</TD> <TD valign="top"> ''Itogi Nauk. Algebra. Topol. Geom. 1966'' (1968) pp. 99–102</TD></TR> | ||
| + | <TR><TD valign="top">[6]</TD> <TD valign="top"> M. Satyanarayana, "Positively ordered semigroups" , M. Dekker (1979)</TD></TR> | ||
| + | <TR><TD valign="top">[7]</TD> <TD valign="top"> E.Ya. Gabovich, "Fully ordered semigroups and their applications" ''Russian Math. Surveys'' , '''31''' : 1 (1976) pp. 147–216 ''Uspekhi Mat. Nauk'' , '''31''' : 1 (1976) pp. 137–201</TD></TR> | ||
| + | </table> | ||
| + | |||
| + | {{TEX|part}} | ||
Revision as of 16:39, 11 June 2016
A semi-group equipped with a (generally speaking, partial) order $\le$ which is stable relative to the semi-group operation, i.e. for any elements $a,b,c$ it follows from $a \le b$ that $ac \le bc$ and $ca \le cb$. If the relation $\le$ on the ordered semi-group $S$ is a total order, then $S$ is called a totally ordered semi-group (cf. also Totally ordered set). If the relation $\le$ on $S$ defines a lattice (with the associated operations join $\vee$ and meet $\wedge$) satisfying the identities $$ c(a \vee b) = ca \vee cb\ \ \text{and}\ \ (a \vee b)c = ac \vee bc $$ then $S$ is called a lattice-ordered semi-group; thus, the class of all lattice-ordered semi-groups, considered as algebras with semi-group and lattice operations, is a variety (cf. also Variety of groups). On a lattice-ordered semi-group the identities $$ c(a \wedge b) = ca \wedge cb\ \ \text{and}\ \ (a \wedge b)c = ac \wedge bc $$ generally speaking, are not required to hold, and their imposition singles out a proper subvariety of the variety of all lattice-ordered semi-groups.
Ordered semi-groups arise by considering different numerical semi-groups, semi-groups of functions and binary relations, semi-groups of subsets (or subsystems of different algebraic systems, for example ideals in rings and semi-groups), etc. Every ordered semi-group is isomorphic to a certain semi-group of binary relations, considered as an ordered semi-group, where the order is set-theoretic inclusion. The classical example of a lattice-ordered semi-group is the semi-group of all binary relations on an arbitrary set.
In the general theory of ordered semi-groups one can distinguish two main developments: the theory of totally ordered semi-groups and the theory of lattice-ordered semi-groups. Although every totally ordered semi-group is lattice-ordered, both theories have developed to a large degree independently. The study of totally ordered semi-groups is devoted to properties that are to a large extent not shared by lattice-ordered semi-groups, while in considering lattice-ordered semi-groups one studies as a rule properties which, when applied to totally ordered semi-groups, reduce to degenerate cases. An important type of semi-groups is formed by the ordered groups (cf. Ordered group); their theory forms an independent part of algebra. In distinction to ordered groups, the order relation on an arbitrary ordered semi-group $S$ is, generally speaking, not defined by the set of its positive elements (i.e. the elements $a$ such that $ax \ge x$ and $xa \ge x$ for any $x$).
Totally ordered semi-groups.
A semi-group $S$ is called orderable if one can define on it a total order which turns it into a totally ordered semi-group. A necessary condition for orderability is the absence in the semi-group of non-idempotent elements of finite order. If in an orderable semi-group the set of all idempotents is non-empty, then it is a sub-semi-group. Among the orderable semi-groups are the free semi-groups, the free commutative semi-groups, and the free $n$-step nilpotent semi-groups. There exists a continuum of methods for ordering free semi-groups of finite rank $\ge 2$. Certain necessary and sufficient conditions for the orderability of arbitrary semi-groups have been found, as well as for semi-groups from a series of known classes (e.g. semi-groups of idempotents, inverse semi-groups).
The structure of totally ordered semi-groups of idempotents has been completely described; in particular, the decomposition of such semi-groups into semi-lattices of rectangular semi-groups (cf. Idempotents, semi-group of) whose rectangular components are singular while the corresponding semi-lattices are trees. The completely-simple totally ordered semi-groups are exhausted by the right groups and the left groups and are lexicographic products (cf. Lexicographic order) of totally ordered groups and totally ordered semi-groups of right (respectively, left) zeros. By applying the reduction to totally ordered groups, a description of totally ordered semi-groups has been obtained in terms of the class of Clifford semi-groups, as well as a characterization in this way of the inverse totally ordered semi-groups (cf. Inversion semi-group). All types of totally ordered semi-groups generated by two mutually inverse elements have been classified (cf. Regular element).
The conditions imposed in the study of totally ordered semi-groups often postulate additional connections between the operation and the order relation. In this way one distinguishes the following basic types of totally ordered semi-groups: Archimedean semi-groups, naturally totally ordered semi-groups (cf. Naturally ordered groupoid), positive ordered semi-groups (in which all elements are positive), integral totally ordered semi-groups (in which 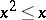 for all
for all  ). Every Archimedean naturally totally ordered semi-group is commutative; their structure is completely described. The structure of an arbitrary totally ordered semi-group is to a large extent determined by the peculiarities of its decomposition into Archimedean classes (cf. Archimedean class). For a periodic totally ordered semi-group this decomposition coincides with the decomposition into torsion classes, and, moreover, each Archimedean class is a nil semi-group. An arbitrary totally ordered nil semi-group is the union of an increasing sequence of convex nilpotent sub-semi-groups; in particular, it is locally nilpotent.
). Every Archimedean naturally totally ordered semi-group is commutative; their structure is completely described. The structure of an arbitrary totally ordered semi-group is to a large extent determined by the peculiarities of its decomposition into Archimedean classes (cf. Archimedean class). For a periodic totally ordered semi-group this decomposition coincides with the decomposition into torsion classes, and, moreover, each Archimedean class is a nil semi-group. An arbitrary totally ordered nil semi-group is the union of an increasing sequence of convex nilpotent sub-semi-groups; in particular, it is locally nilpotent.
A homomorphism 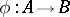 of totally ordered semi-groups is called an
of totally ordered semi-groups is called an  -homomorphism if
-homomorphism if 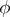 is an isotone mapping from
is an isotone mapping from 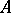 to
to 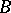 . A congruence (cf. Congruence (in algebra)) on a totally ordered semi-group is called an
. A congruence (cf. Congruence (in algebra)) on a totally ordered semi-group is called an  -congruence if all its classes are convex subsets; the kernel congruences of
-congruence if all its classes are convex subsets; the kernel congruences of  -homomorphisms are precisely the
-homomorphisms are precisely the  -congruences. The decomposition of a totally ordered semi-group
-congruences. The decomposition of a totally ordered semi-group 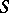 into Archimedean classes does not always define
into Archimedean classes does not always define  -congruences, i.e. they are not always a band (cf. Band of semi-groups), but this is so, for example, if
-congruences, i.e. they are not always a band (cf. Band of semi-groups), but this is so, for example, if 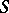 is periodic and its idempotents commute or if
is periodic and its idempotents commute or if 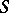 is a positive totally ordered semi-group.
is a positive totally ordered semi-group.
For a totally ordered semi-group there arises an additional condition of simplicity (cf. Simple semi-group), related to the order. One such condition is the lack of proper convex ideals (convex ideally-simple, or  -simple, semi-groups); a trivial example of such a totally ordered semi-group is a totally ordered group. A totally ordered semi-group
-simple, semi-groups); a trivial example of such a totally ordered semi-group is a totally ordered group. A totally ordered semi-group 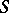 with a least element
with a least element  and a greatest element
and a greatest element 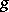 (in particular, finite) will be convex ideally simple if and only if
(in particular, finite) will be convex ideally simple if and only if  and
and 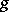 are at the same time left and right zeros in
are at the same time left and right zeros in 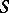 . Any totally ordered semi-group may be imbedded, while preserving the order (
. Any totally ordered semi-group may be imbedded, while preserving the order ( -isomorphically), in a convex ideally-simple totally ordered semi-group. There exist totally ordered semi-groups with cancellation, non-imbeddable in a group, but a commutative totally ordered semi-group with cancellation can be
-isomorphically), in a convex ideally-simple totally ordered semi-group. There exist totally ordered semi-groups with cancellation, non-imbeddable in a group, but a commutative totally ordered semi-group with cancellation can be  -isomorphically imbedded in an Abelian totally ordered group; moreover, there exists a unique group of fractions, up to an
-isomorphically imbedded in an Abelian totally ordered group; moreover, there exists a unique group of fractions, up to an  -isomorphism. A totally ordered semi-group is
-isomorphism. A totally ordered semi-group is  -isomorphically imbeddable in the additive group of real numbers if and only if it satisfies the cancellation law and contains no abnormal pair (i.e. elements
-isomorphically imbeddable in the additive group of real numbers if and only if it satisfies the cancellation law and contains no abnormal pair (i.e. elements 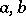 such that either
such that either 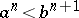 ,
, 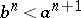 for all
for all 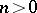 , or
, or  ,
, 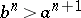 for all
for all  ).
).
Lattice-ordered semi-groups.
If for two elements  and
and 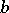 in an ordered semi-group there exists a greatest element
in an ordered semi-group there exists a greatest element  with the property
with the property  , then it is called a right quotient and is denoted by
, then it is called a right quotient and is denoted by 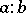 , the left quotient
, the left quotient 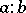 is defined similarly. A lattice-ordered semi-group
is defined similarly. A lattice-ordered semi-group 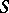 is called a lattice-ordered semi-group with division if the right and left quotients exist in
is called a lattice-ordered semi-group with division if the right and left quotients exist in 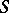 for any pair of elements. Such semi-groups are complete (as a lattice) lattice-ordered semi-groups, their lattice zero is also the multiplicative zero and they satisfy the infinite distributive laws
for any pair of elements. Such semi-groups are complete (as a lattice) lattice-ordered semi-groups, their lattice zero is also the multiplicative zero and they satisfy the infinite distributive laws 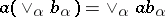 ,
, 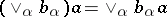 . An important example of a lattice-ordered semi-group with division is the multiplicative semi-group of ideals of an associative ring, and a notable direction in the theory of lattice-ordered semi-groups deals with the transfer of many properties and results from the theory of ideals in associative rings to the case of lattice-ordered semi-groups (the unique decomposition into prime factors, primes, primary, maximal, principal elements of a lattice-ordered semi-group, etc.). For example, the well-known relation of Artin in the theory of commutative rings can be translated as follows in the theory of lattice-ordered semi-groups with division and having a one 1: Let
. An important example of a lattice-ordered semi-group with division is the multiplicative semi-group of ideals of an associative ring, and a notable direction in the theory of lattice-ordered semi-groups deals with the transfer of many properties and results from the theory of ideals in associative rings to the case of lattice-ordered semi-groups (the unique decomposition into prime factors, primes, primary, maximal, principal elements of a lattice-ordered semi-group, etc.). For example, the well-known relation of Artin in the theory of commutative rings can be translated as follows in the theory of lattice-ordered semi-groups with division and having a one 1: Let 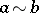
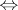
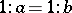 . If the lattice-ordered semi-group
. If the lattice-ordered semi-group 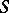 being considered is commutative, then the relation
being considered is commutative, then the relation 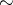 is a congruence on it; moreover, the quotient semi-group
is a congruence on it; moreover, the quotient semi-group 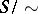 is a (lattice-ordered) group if and only if
is a (lattice-ordered) group if and only if 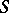 is integrally closed, i.e.
is integrally closed, i.e. 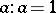 for every
for every 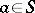 .
.
The study of lattice-ordered semi-groups is connected with groups by considering the imbedding problems of a lattice-ordered semi-group in a lattice-ordered group. For example, every lattice-ordered semi-group with cancellation and the Ore condition (cf. Imbedding of semi-groups) and whose multiplication is distributive relative to both lattice operations, is imbeddable in a lattice-ordered group.
The theory of lattice-ordered semi-groups has begun to be studied from the point of view of the theory of varieties: the free lattice-ordered semi-groups have been described, the minimal varieties of lattice-ordered semi-groups have been found, etc.
References
| [1] | L. Fuchs, "Partially ordered algebraic systems" , Pergamon (1963) |
| [2] | G. Birkhoff, "Lattice theory" , Colloq. Publ. , 25 , Amer. Math. Soc. (1973) |
| [3] | A.I. Kokorin, V.M. Kopytov, "Fully ordered groups" , Israel Program Sci. Transl. (1974) (Translated from Russian) |
| [4] | Itogi Nauk. Algebra. Topol. Geom. 1965 (1967) pp. 116–120 |
| [5] | Itogi Nauk. Algebra. Topol. Geom. 1966 (1968) pp. 99–102 |
| [6] | M. Satyanarayana, "Positively ordered semigroups" , M. Dekker (1979) |
| [7] | E.Ya. Gabovich, "Fully ordered semigroups and their applications" Russian Math. Surveys , 31 : 1 (1976) pp. 147–216 Uspekhi Mat. Nauk , 31 : 1 (1976) pp. 137–201 |
Ordered semi-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ordered_semi-group&oldid=38959