Band of semi-groups
of a given family 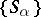
A semi-group 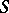 that has a partition into sub-semi-groups whose (isomorphism) classes are just the semi-groups
that has a partition into sub-semi-groups whose (isomorphism) classes are just the semi-groups 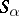 , and such that for any
, and such that for any 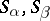 there is an
there is an 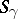 such that
such that 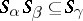 .
. 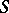 is also said to be decomposable into the band of semi-groups
is also said to be decomposable into the band of semi-groups 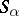 . In other words,
. In other words, 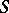 has a partition into a band of semi-groups
has a partition into a band of semi-groups 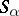 if all the
if all the 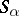 are sub-semi-groups of
are sub-semi-groups of 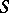 and if there is a congruence
and if there is a congruence 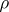 on
on 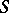 such that the
such that the 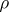 -classes are just the
-classes are just the 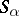 . The semi-groups
. The semi-groups 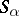 are called the components of the given band. The term "band of semi-groups" is consistent with the frequent use of the word "band20M14band" as a synonym of "semi-group all elements of which are idempotents" , since a congruence
are called the components of the given band. The term "band of semi-groups" is consistent with the frequent use of the word "band20M14band" as a synonym of "semi-group all elements of which are idempotents" , since a congruence 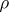 on a semi-group
on a semi-group 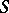 determines a partition of
determines a partition of 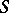 into a band if and only if the quotient semi-group
into a band if and only if the quotient semi-group 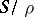 is a semi-group of idempotents.
is a semi-group of idempotents.
Many semi-groups are decomposable into a band of semi-groups with one or other "better" property; thus, the study of their structure is reduced in some measure to a consideration of the types to which the components of a band belong, and of semi-groups of idempotents (see, e.g. Archimedean semi-group; Completely-simple semi-group; Clifford semi-group; Periodic semi-group; Separable semi-group).
A band of semi-groups 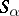 is said to be commutative if for the corresponding congruence
is said to be commutative if for the corresponding congruence 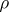 the quotient semi-group
the quotient semi-group 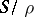 is commutative; then
is commutative; then 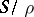 is a semi-lattice (in this case,
is a semi-lattice (in this case, 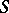 is frequently called a semi-lattice of semi-groups
is frequently called a semi-lattice of semi-groups 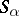 ; in particular, if
; in particular, if 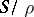 is a chain, then
is a chain, then 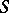 is called a chain of semi-groups
is called a chain of semi-groups 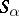 ). A band of semi-groups is called rectangular (sometimes matrix) if
). A band of semi-groups is called rectangular (sometimes matrix) if 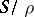 is a rectangular semi-group (see Idempotents, semi-group of). Equivalently, if the components of the band can be indexed by pairs of indices
is a rectangular semi-group (see Idempotents, semi-group of). Equivalently, if the components of the band can be indexed by pairs of indices 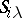 , where
, where 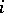 and
and 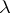 run over certain sets
run over certain sets 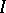 and
and 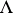 , respectively, such that for any
, respectively, such that for any 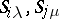 one has
one has 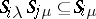 . Any band of semi-groups is a semi-lattice of rectangular bands, that is, its components can be arranged into subfamilies so that the union of the components of each subfamily is a rectangular band of components, and the original semi-group is decomposable into a semi-lattice of these unions (Clifford's theorem [1]). Since the properties of being a semi-group of idempotents, a semi-lattice or a rectangular semi-group are characterized by identities, for each of the listed properties
. Any band of semi-groups is a semi-lattice of rectangular bands, that is, its components can be arranged into subfamilies so that the union of the components of each subfamily is a rectangular band of components, and the original semi-group is decomposable into a semi-lattice of these unions (Clifford's theorem [1]). Since the properties of being a semi-group of idempotents, a semi-lattice or a rectangular semi-group are characterized by identities, for each of the listed properties  there is a finest congruence on any semi-group
there is a finest congruence on any semi-group 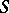 for which the corresponding quotient semi-group has the property
for which the corresponding quotient semi-group has the property 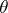 , that is, there exist greatest (or biggest quotient) partitions of
, that is, there exist greatest (or biggest quotient) partitions of 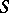 into a band of semi-groups, into a commutative band of semi-groups and into a rectangular band of semi-groups.
into a band of semi-groups, into a commutative band of semi-groups and into a rectangular band of semi-groups.
The term strong band concerns special types of bands of semi-groups [4]: For any elements  and
and  from different components, the product
from different components, the product 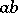 is a power of one of these elements. An important special case of a strong band, and also a special case of a chain of semi-groups, is the ordinal sum (or sequentially-annihilating band): The set of its components
is a power of one of these elements. An important special case of a strong band, and also a special case of a chain of semi-groups, is the ordinal sum (or sequentially-annihilating band): The set of its components 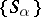 is totally ordered, and for any
is totally ordered, and for any 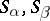 such that
such that 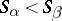 , and for any
, and for any 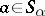 ,
, 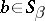 one has
one has 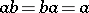 ; the ordinal sum is defined uniquely up to an isomorphism, by specifying the components and their ordering.
; the ordinal sum is defined uniquely up to an isomorphism, by specifying the components and their ordering.
References
| [1] | A.H. Clifford, "Bands of semi-groups" Proc. Amer. Math. Soc. , 5 (1954) pp. 499–504 |
| [2] | A.H. Clifford, G.B. Preston, "Algebraic theory of semi-groups" , 1 , Amer. Math. Soc. (1961) |
| [3] | E.S. Lyapin, "Semigroups" , Amer. Math. Soc. (1974) (Translated from Russian) |
| [4] | L.N. Shevrin, "Strong bands of semi-groups" Izv. Vyssh. Uchebn. Zaved. Mat. : 6 (1965) pp. 156–165 (In Russian) |
Comments
A congruence on a semi-group 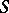 is an equivalence relation such that for all
is an equivalence relation such that for all 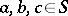 one has
one has
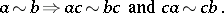 |
Band of semi-groups. L.N. Shevrin (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Band_of_semi-groups&oldid=18665