Difference between revisions of "Siegel method"
(Importing text file) |
m (link) |
||
| Line 1: | Line 1: | ||
| − | A method for investigating the arithmetical properties of the values assumed at algebraic points by | + | A method for investigating the arithmetical properties of the values assumed at algebraic points by [[E-function|$E$-function]]s that satisfy linear differential equations with coefficients in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s085/s085000/s0850002.png" />; first proposed by C.L. Siegel [[#References|[1]]]. |
An entire function | An entire function | ||
Revision as of 21:22, 16 January 2016
A method for investigating the arithmetical properties of the values assumed at algebraic points by $E$-functions that satisfy linear differential equations with coefficients in 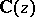 ; first proposed by C.L. Siegel [1].
; first proposed by C.L. Siegel [1].
An entire function
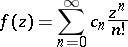 |
is called an 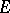 -function if all its coefficients
-function if all its coefficients 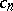 belong to an algebraic field of finite degree (cf. Algebraic number; Field), if for every
belong to an algebraic field of finite degree (cf. Algebraic number; Field), if for every 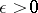 the maximum modulus of the
the maximum modulus of the 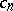 is
is 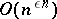 and if there exists a sequence of rational integers
and if there exists a sequence of rational integers 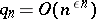 such that
such that 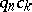 is an algebraic integer for
is an algebraic integer for 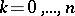 . Examples are
. Examples are 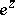 ,
, 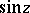 and the Bessel function
and the Bessel function 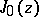 (cf. Bessel functions).
(cf. Bessel functions).
Let 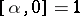 , and
, and 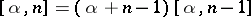 ,
, 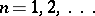 . If
. If  and
and 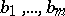 are rational numbers,
are rational numbers, 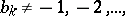 and
and 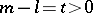 , then the function
, then the function
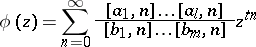 |
is an 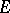 -function; it satisfies a linear differential equation of order
-function; it satisfies a linear differential equation of order 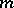 with coefficients in
with coefficients in 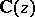 .
.
Siegel's main result pertains to the values of the function
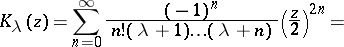 |
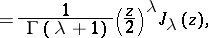 |
where 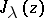 is the Bessel function. If
is the Bessel function. If 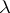 is a rational number,
is a rational number, 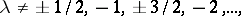 then for any algebraic number
then for any algebraic number  the numbers
the numbers 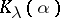 and
and 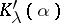 are algebraically independent over
are algebraically independent over 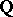 (cf. Algebraic independence).
(cf. Algebraic independence).
In 1949 Siegel presented his method in a general setting, but the conditions that had to be imposed on the 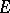 -functions
-functions 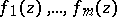 so that their values could be assumed algebraically independent proved to be very hard to check. He was therefore unable to achieve any concrete new results.
so that their values could be assumed algebraically independent proved to be very hard to check. He was therefore unable to achieve any concrete new results.
Further development and generalization of Siegel's method should be credited to A.B. Shidlovskii (see [2]–[3]): Let 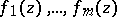 be
be 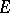 -functions which constitute a solution to the system of differential equations
-functions which constitute a solution to the system of differential equations
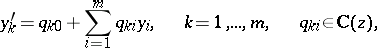 | (1) |
and let 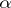 be an algebraic number distinct from zero and from the singular points of the system (1); then the
be an algebraic number distinct from zero and from the singular points of the system (1); then the 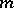 numbers
numbers 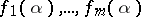 are algebraically independent over
are algebraically independent over 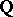 if and only if the functions
if and only if the functions 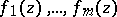 are algebraically independent over
are algebraically independent over 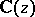 . This theorem implies, in particular, that if
. This theorem implies, in particular, that if 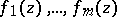 are algebraically independent, then all the numbers
are algebraically independent, then all the numbers 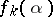 are transcendental (cf. Transcendental number); the same holds for all non-zero
are transcendental (cf. Transcendental number); the same holds for all non-zero 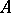 -points of the functions
-points of the functions 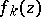 distinct from the poles of the system (1), provided
distinct from the poles of the system (1), provided 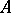 is algebraic. The theorem has produced a great number of results concerning specific
is algebraic. The theorem has produced a great number of results concerning specific 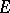 -functions, and algebraic independence proofs for values of
-functions, and algebraic independence proofs for values of 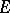 -functions satisfying linear homogeneous and inhomogeneous differential equations of order higher than two. For example, the function
-functions satisfying linear homogeneous and inhomogeneous differential equations of order higher than two. For example, the function
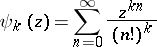 |
satisfies a linear differential equation of order 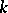 with coefficients in
with coefficients in 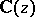 ; it can be proved that for any algebraic number
; it can be proved that for any algebraic number 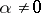 , the
, the 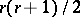 numbers
numbers 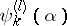 ,
, 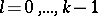 ;
; 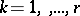 , are algebraically independent over
, are algebraically independent over 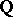 .
.
Under the same conditions, the maximum number of numbers 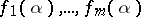 which are algebraically independent over
which are algebraically independent over 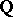 is equal to the maximum number of functions
is equal to the maximum number of functions 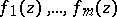 which are algebraically independent over
which are algebraically independent over 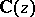 . If
. If 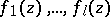 are
are 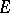 -functions that are algebraically independent over
-functions that are algebraically independent over 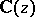 and that satisfy the system (1), then for all points
and that satisfy the system (1), then for all points 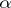 , with the possible exception of finitely many, the numbers
, with the possible exception of finitely many, the numbers 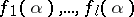 are algebraically independent over
are algebraically independent over 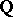 . In each specific case the exceptional points can actually be determined.
. In each specific case the exceptional points can actually be determined.
These theorems provide the solution to virtually all problems of a general nature concerning transcendence and algebraic independence of the values of 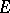 -functions at algebraic points.
-functions at algebraic points.
Siegel's methods enables one to estimate the measure of algebraic independence of the numbers 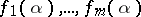 , thus giving the results a quantitative form. If the functions
, thus giving the results a quantitative form. If the functions 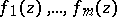 are algebraically independent, then
are algebraically independent, then 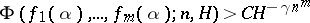 , where
, where 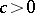 is independent of
is independent of 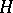 and
and 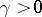 depends only on
depends only on  and the degree of the algebraic number
and the degree of the algebraic number 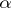 .
.
References
| [1] | C.L. Siegel, "Ueber einige Anwendungen Diophantischer Approximationen" Abh. Deutsch. Akad. Wiss. Phys.- Math. Kl. : 1 (1929) pp. 1–41 |
| [2] | A.B. Shidlovskii, "On tests for algebraic independence of the values of a class of entire functions" Izv. Akad. Nauk SSSR Ser. Mat. , 23 : 1 (1959) pp. 35–66 (In Russian) |
| [3] | A.B. Shidlovskii, "On transcendency and algebraic independence of values of 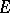 -functions related with an arbitrary number of algebraic equations in the rational function field" Izv. Akad. Nauk SSSR Ser. Mat. , 26 : 6 (1962) pp. 877–910 (In Russian) -functions related with an arbitrary number of algebraic equations in the rational function field" Izv. Akad. Nauk SSSR Ser. Mat. , 26 : 6 (1962) pp. 877–910 (In Russian) |
| [4] | A.B. Shidlovskii, "On arithmetic properties of values of analytic functions" Proc. Steklov Inst. Math. , 132 (1972) pp. 193–233 Trudy Mat. Inst. Steklov. , 132 (1972) pp. 169–202 |
| [5] | S. Lang, "A transcendence measure for 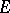 -functions" Mathem. , 9 (1962) pp. 157–161 -functions" Mathem. , 9 (1962) pp. 157–161 |
| [6] | N.I. Fel'dman, A.B. Shidlovskii, "The development and present state of the theory of transcendental numbers" Russian Math. Surveys , 22 : 3 (1967) pp. 1–79 Uspekhi Mat. Nauk , 22 : 3 (1967) pp. 3–81 |
Comments
In the article above, 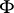 is the measure of algebraic independence, cf. Algebraic independence, measure of.
is the measure of algebraic independence, cf. Algebraic independence, measure of.
References
| [a1] | A.B. Shidlovskii, "Transcendental numbers" , de Gruyter (1989) (Translated from Russian) |
| [a2] | Y. André, " -functions" , Vieweg (1989) -functions" , Vieweg (1989) |
Siegel method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Siegel_method&oldid=37572